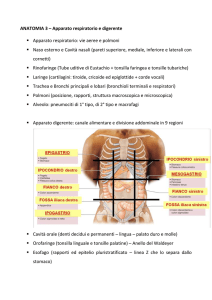
Journal Club di Neuroscienze
Martedì (grasso) 24 Febbraio 2009
Articolo:
“Stable Irregular Dynamics in Complex Neural
Networks”
S. Jahnke, R.-M. Memmesheimer and M. Timme
Phys. Rev. Lett. 100:048102 (2008)
Presentato da:
Dott. Massimo Calamai
Premesse
●
Dinamiche altamente irregolari DAI (caos)
●
reti di spiking neurons
●
●
reti sparse=>balance state
(#inibitori=#eccitatori): le fluttuazioni
creano gli spikes (Poisson)
reti inibitorie, accoppiamenti globali, un
po' diluite, senza ritardo DAI sono stabili
(max Lyapunov exp, Zillmer et al.)
Conclusioni (???)
●
dinamica microscopica reti finite con:
–
interazioni inibitorie e ritardate
–
connettività arbitrariamente complicata
●
e` stabile
●
qualsiasi orbita periodica e` stabile
●
DAI non e` caotica
Modello
●
●
N neuroni
dinamica sotto soglia del potenziale di
membrana:
●
●
●
descrizione equivalente:
Modello
●
dopo un ritardo dal neurone j al neurone i:
●
●
●
interazione mediata da funzione di
trasferimento:
●
●
mappa one-to-one:
Un po' di figure
●
●
attivita` tipica: sequenze irregolari di
spikes
e` caotica?
Dinamica microscopica 1
●
traiettoria originale e piccola perturbazione
●
●
se all'evento (n+1)-esimo j* spara
●
●
a un certo tempo t: i riceve j*
●
●
●
applicando TVM
Dinamica microscopica 2
●
●
se j* non e` connesso con i: rimane
invariato
se j* e` connesso con i
●
●
●
sappiamo che la fase dipende dal modello
poiche' la mappa e` monotona e concava:
trovano che indipendentemente dal
modello e dalla traiettoria,
Dinamica microscopica 3
●
●
●
●
lo shift massimo non puo` aumentare e il
minimo non puo` diminuire (Lyapunov
stabili)
per reti fortemente connesse si ha anche
convergenza esponenziale
le perturbazioni di tutti i neuroni tendono
a essere identiche
shift temporale dell'orbita originale
Ancora figure
Dinamica microscopica 4
●
●
●
●
condizione stabilita`: ordine degli eventi
rimane uguale
taglia non-zero di perturbazione che lo
lascia invariato per ogni intervallo di
tempo finito
margine temporale rimane piu` grande
della perturbazione per tempo infinito
orbite periodiche fatte da P eventi sono
stabili perche' c'e` un margine minimo
Dinamica microscopica 5
●
stabilita` di sequenze di spike irregolari
●
balance state (Poisson) rate
●
probabilita` che margine minimo sia piu`
piccolo o uguale a
●
●
decadimento algebrico margine minimo
Ultime considerazioni
●
sequenze arbitrariamente irregolari di
spike convergono su un orbita periodica
dopo tempo finito
–
1. esiste numero E : due sequenze
equamente ordinate
–
2. c'e` solo un numero finito di ordinamenti di
eventi in rete finita
Fine
Grazie della cortese attenzione
MC