E - P. Hensemberger

5B1
elementi di linee elettriche: linee R-L
3. elementi di linee elettriche: LINEE R-L
• calcolo elettrico delle linee R-L
•
•
•
•
•
calcolo di progetto e verifica
criterio della perdita di potenza ammissibile
criterio della temperatura ammissibile
criterio della caduta di tensione ammissibile
metodo della caduta di tensione unitaria
3.
• esercizi
TPS
2015/2016
a.s. 2012/2013
L. Agarossi - ITIS “P. Hensemberger - Monza -
1
5B1
tipologia di linea R-L
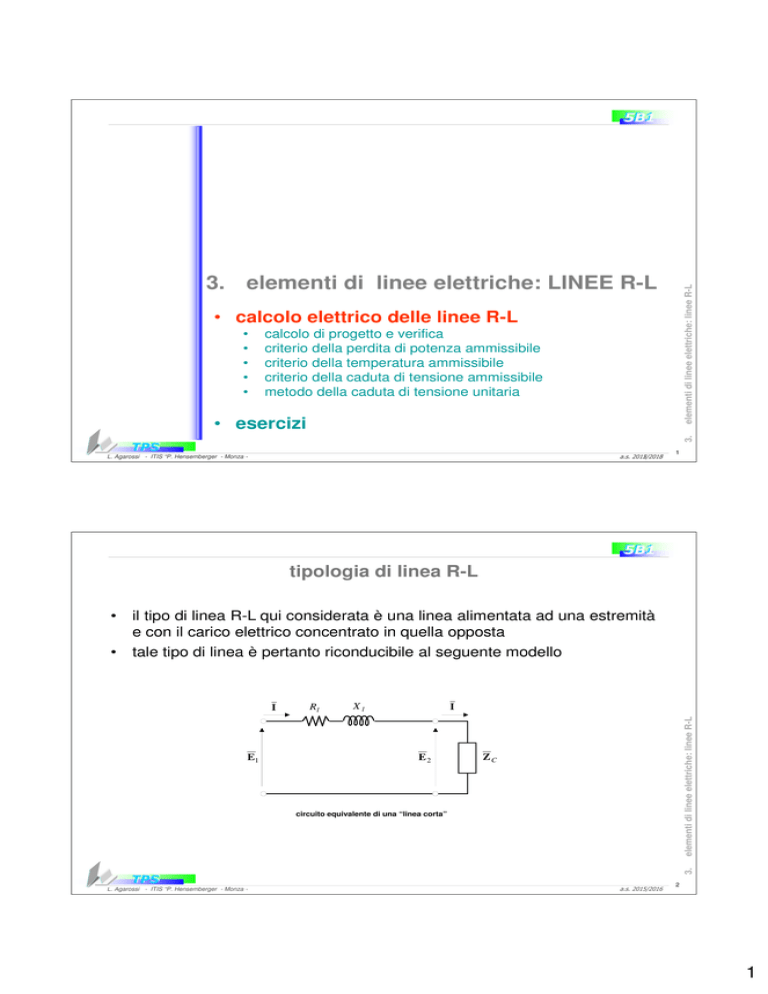
• il tipo di linea R-L qui considerata è una linea alimentata ad una estremità
e con il carico elettrico concentrato in quella opposta
• tale tipo di linea è pertanto riconducibile al seguente modello
E1
Rl
Xl
I
E2
elementi di linee elettriche: linee R-L
I
ZC
3.
circuito equivalente di una “linea corta”
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
2
1
5B1
calcolo elettrico delle linee R-L
• calcolare una linea elettrica significa sostanzialmente
– determinare la sezione teorica e commerciale dei conduttori
– verificare le condizioni operative di
• portata
• caduta di tensione in linea
elementi di linee elettriche: linee R-L
• aumento della temperatura
– verificare le condizioni di guasto
• correnti di cortocircuito
3.
• interazione linea/apparati di protezione
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
3
5B1
calcolo di progetto e di verifica
elementi di linee elettriche: linee R-L
• il calcolo di progetto di una linea elettrica consiste nel determinare le
caratteristiche fisiche della conduttura (sezione dei conduttori, tipo di
cavo, modalità di posa, etc.) in funzione dei dati di ingresso e nel rispetto
di determinati vincoli progettuali che andranno verificati a calcolo
concluso
3.
• il calcolo di verifica di una linea elettrica consiste nel controllare che
una conduttura elettrica esistente, in seguito a modifiche intervenute nel
suo regime di funzionamento, continui a possedere determinati requisiti e
a soddisfare i vincoli prefissati
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
4
2
5B1
criteri per il calcolo di progetto e di verifica
• il calcolo di progetto e di verifica di una linea R-L si basa essenzialmente
su tre criteri:
• criterio della perdita di potenza ammissibile
elementi di linee elettriche: linee R-L
– usato prevalentemente per le linee aeree
• criterio della caduta di tensione ammissibile
– usato prevalentemente per le linee in cavo
• criterio della temperatura ammissibile
3.
– usato prevalentemente a linee con conduttori nudi
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
5
5B1
•
il criterio della perdita di potenza ammissibile, prevalentemente usato per le linee
aeree, consiste nel fissare un valore percentuale della perdita di potenza
ammissibile (∆p%) in linea e da questo determinare la sezione S dei conduttori
•
i valori di ∆p% praticamente usati sono compresi fra il 2% e l’ 8% della potenza
trasmessa con valori più piccoli per linee ad alta tensione
•
la determinazione della sezione dipende dal regime di correnti in linea e
contempla quindi i seguenti tre casi
elementi di linee elettriche: linee R-L
criterio della perdita di potenza ammissibile
3.
– linea in corrente continua
– linea in corrente alternata monofase
– linea in corrente alternata trifase
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
6
3
criterio della perdita di potenza ammissibile:
5B1
corrente continua
indicando con Rl la resistenza di linea relativa ad un conduttore. Con L la
lunghezza e con I la corrente di linea, la potenza persa nei due conduttori è data
da
2
∆ p = 2 Rl I
ed essendo
P
I =
V
L
Rl = ρ ;
S
si ottiene
∆p =
elementi di linee elettriche: linee R-L
•
2 ρ LP 2
SV
2
da cui si ricava la sezione dei conduttori di linea
∆ pV
2
3.
S=
2 ρ LP
2
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
criterio della perdita di potenza ammissibile:
7
5B1
corrente alternata monofase
•
nel caso di corrente alternata l’espressione della corrente è data dalla relazione
P
I =
V cos ϕ
L
Rl = ρ ;
S
si ottiene
∆p =
P
I =
V cos ϕ
2 ρ LP
elementi di linee elettriche: linee R-L
ed essendo
2
SV 2 cos 2 ϕ
da cui si ricava la sezione dei conduttori di linea
2
2
∆ pV cos ϕ
3.
S=
2 ρ LP
2
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
8
4
criterio della perdita di potenza ammissibile:
5B1
corrente alternata trifase
nel caso di corrente alternata trifase, essendo tre i conduttori sarà
∆ p = 3 Rl I
ed essendo
L
Rl = ρ ;
S
si ottiene
∆p = 3
ρL
I =
P
2
2
P
3V cos ϕ
2
2
S 3V cos ϕ
=
ρ LP
2
elementi di linee elettriche: linee R-L
•
2
2
SV cos ϕ
da cui si ricava la sezione dei conduttori di linea
2
2
∆ pV cos ϕ
3.
S=
ρ LP
2
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
criterio della perdita di potenza ammissibile:
9
5B1
sezione in funzione della perdita di potenza %
•
volendo esprimere la sezione in funzione della perdita di potenza percentuale
∆P
100
∆p % =
P
S=
S=
∆ p %V
per la corrente continua
2
200 ρ LP
2
2
per la corrente alternata monofase
∆ p %V cos ϕ
100 ρ LP
2
2
per la corrente alternata trifase
∆ p %V cos ϕ
3.
S=
200 ρ LP
elementi di linee elettriche: linee R-L
si ottengono le seguenti espressioni
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
10
5
5B1
il criterio della caduta di tensione ammissibile si usa prevalentemente per linee in
cavo di lunghezza ≥30m specie se funzionanti in bassa tensione ma è anche
utilizzabile per le linee aeree
•
nel caso dei cavi, dopo aver calcolato la sezione del conduttore in base alla
caduta di tensione ammissibile, occorre sempre verificare che la portata
corrispondente non sia inferiore alla corrente di esercizio
•
come caduta di tensione ammissibile si considera, in generale, la caduta di
tensione industriale riferita alla tensione di arrivo
•
nel caso di impianti utilizzatori con tensione nominale fino a 1000 V in corrente
alternata e 1500V in corrente continua, l’art. 525 della norma CEI 64-8
raccomanda che la caduta di tensione tra l’origine dell’impianto utilizzatore e
qualunque apparecchio utilizzatore non sia superiore al 4% della tensione
nominale dell’impianto
3.
•
elementi di linee elettriche: linee R-L
criterio della caduta di tensione ammissibile
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
11
5B1
criterio della caduta di tensione ammissibile
•
la caduta di tensione ammissibile viene in genere espressa in forma percentuale
•
tenendo conto dell’espressione della caduta di tensione industriale e dei regimi di
corrente in linea, si hanno le seguente tre relazioni:
∆V
3 IL
∆V % =
100 =
( rl cos ϕ + x l sen ϕ )100
V2
V2
→ caduta di tensione percentuale per una
∆V
2 IL
∆E % =
100 =
( rl cos ϕ + x l sen ϕ )100
E2
E2
→ caduta di tensione percentuale per una
2 ILrl
∆V
100 =
100
∆V % =
V2
V2
→ caduta di tensione percentuale per una
linea monofase
3.
linea in corrente continua
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
elementi di linee elettriche: linee R-L
linea trifase
a.s. 2015/2016
12
6
5B1
criterio della caduta di tensione ammissibile: procedura di calcolo
START
dati del problema
dati del problema
si fissa ∆Vam
ammissibile
si fissa ∆Vam
ammissibile
si determina la
sezione del cavo S
si sceglie il cavo con
portata Iz>I
si valuta da tabella la
portata Iz del cavo
si calcola la ∆V del
cavo scelto
Iz>I ?
NO
∆V≤∆Vam ?
si sceglie il cavo di
sezione superiore
elementi di linee elettriche: linee R-L
SI
START
NO
SI
si aumenta S per
avere Iz>I
cavo OK
cavo OK
END
END
procedura di calcolo con verifica di caduta di tensione
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
procedura di calcolo con verifica di corrente
13
5B1
criterio della caduta di tensione ammissibile: applicazione
•
per l’applicazione delle procedure di calcolo, dopo aver fissato il valore di ∆V%;
si procede secondo i seguenti passi
– si ritiene pari al valore nominale la tensione all’arrivo della linea;
– si stabilisce un valore orientativo della reattanza kilometrica uguale a
• xl=0,4 Ω/km per linee aeree
• xl=0,1 Ω/km per linee in cavo
elementi di linee elettriche: linee R-L
– si calcola la resistenza kilometrica di linea rl dall’espressione della ∆V%;
– si calcola la sezione dei conduttori con la relazione
rl =
ρ
S
⇒ S =
ρ
rl
considerando il valore di resistività in Ωmm2/km alla temperatura di esercizio della
linea;
– si sceglie la sezione commerciale e si verifica che la reattanza effettiva sia poco diversa
da quella ipotizzata in caso contrario si affina il calcolo;
3.
– si prosegue come indicato dalle rispettive flow-chart
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
14
7
5B1
metodo della caduta di tensione unitaria
•
questo metodo, basato sempre sul criterio della caduta di tensione ammissibile,
consente di semplificare il calcolo usando una apposita tabella che dà, per i vari
tipi di cavo (unipolare, bipolare, tripolare), per i vari tipi di corrente(continua,
monofase, trifase) e per due valori convenzionali del cosϕ (0,8 e 1), i valori della
caduta di tensione unitaria in funzione della sezione dei conduttori definita dalla
relazione
elementi di linee elettriche: linee R-L
∆ V ⋅ 1000
u=
IL
espressa in mV/Am (millivolt/ampere metro)essendo ∆V la caduta di tensione espressa in
volt; il valore di u rappresenta la caduta di tensione per ogni metro di cavo e per ogni
ampère di corrente
considerando ad esempio l’espressione della caduta di tensione industriale trifase
si ha
3 IL ( rl cos ϕ + x l sin ϕ )1000
∆ V = 3 IL ( rl cos ϕ + x l sin ϕ ) ⇒ u =
IL
e quindi
u=
TPS
3 ( rl cos ϕ + x l sin ϕ )1000
3.
•
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
15
5B1
metodo della caduta di tensione unitaria: applicazione
•
dalla definizione della caduta di tensione unitaria
u=
3 ( rl cos ϕ + x l sin ϕ )1000
•
elementi di linee elettriche: linee R-L
si deduce che il valore di u dipende, oltre che dall’angolo ϕ , solo dai parametri
costruttivi del cavo e quindi può essere tabulato in funzione della sezione e del
cosϕ. Discorsi analoghi si possono fare per la corrente continua e per l’alternata
monofase
per applicare questo metodo è necessario procedere secondo i seguenti passi:
– fissare il valore di ∆V%;
– calcolare ∆V;
– calcolare u;
3.
– scegliere la sezione del cavo avente una u minore di quella calcolata;
– verificare, tramite tabelle (Tabella 1 e 2 ) che la portata sia sufficiente
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
16
8
5B1
criterio della temperatura ammissibile
•
il criterio della temperatura ammissibile si basa sulla equazione che si ottiene
uguagliando l’energia termica prodotta per effetto Joule in un conduttore e quella
dissipata all’esterno, in condizione di equilibrio termico
•
tale condizione si esprime con la relazione
∆
energia dissipata all’esterno nel tempo ∆t
∆
→ equazione dell’equilibrio termico
Pc = λθ A
elementi di linee elettriche: linee R-L
da cui
energia fornita nel tempo ∆t
Pc ∆ t = λθ A ∆ t
dove Pc è la potenza termica, λ il coefficiente globale di trasmissione termica per
convezione e irraggiamento, A la superficie disperdente e θ∆ la sovratemperatura
i valori di λ si possono scegliere con il seguente criterio
λ = (12 ÷ 16 )
•
W
aria
→
stagnante
2
m K
λ = (15 ÷ 20 )
W
m2K
aria a
→ circolazione per
naturale
θ ∆ = (30 ÷ 90)°C
l’applicazione dell’equazione dell’equilibrio termico avviene in modo diverso a
seconda che si tratti di conduttori a sezione circolare o di barre rettangolari
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
•
17
5B1
criterio della temperatura ammissibile : conduttore a sezione circolare
•
dato un conduttore circolare di diametro d e di lunghezza L, la sezione S e la
superficie disperdente A saranno rispettivamente espresse dalle relazioni
d2
π
S =
4
A = πdL
→ sezione del conduttore
→ superficie disperdente
mentre la potenza termica Pc, dovuta all’effetto Joule, sarà pari a
•
=
ρL
S
I
2
elementi di linee elettriche: linee R-L
Pc = RI
2
l’equazione dell’equilibrio termico
Pc = λθ ∆ A
fatte le relative sostituzioni, assumerà, per un conduttore a sezione circolare, la
seguente espressione
∆
2
4 ρ I = λϑ π d
3
3.
2
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
18
9
5B1
criterio della temperatura ammissibile : barra di sezione rettangolare
•
data una barra di sezione rettangolare di base b di altezza h e di lunghezza L, la
sezione S e la superficie disperdente A saranno
S = bh
A = 2 (b + h ) L
→ sezione del conduttore
→ superficie disperdente
mentre la potenza termica Pc, dovuta all’effetto Joule, sarà pari a
•
=
ρL
S
I
2
elementi di linee elettriche: linee R-L
Pc = RI
2
l’equazione dell’equilibrio termico
∆
Pc = λθ A
fatte le relative sostituzioni, assumerà, per una barra di sezione rettangolare, la
seguente espressione
2
∆
3.
ρ I = 2 λϑ (b + h )bh
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
19
3.
elementi di linee elettriche: linee R-L
5B1
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
20
10
5B1
4-BP
elementi di linee elettriche: linee R-L
elementi di linee elettriche: LINEE R-L
• calcolo elettrico delle linee R- L
•
•
•
•
•
calcolo di progetto e verifica
criterio della perdita di potenza ammissibile
criterio della temperatura ammissibile
criterio della caduta di tensione ammissibile
metodo della caduta di tensione unitaria
3.
• esercizi
impianti elettrici
TPS
2015/2016
a.s. 2012/2013
L. Agarossi - ITIS “P. Hensemberger - Monza -
21
5B1
esercizio 1
esercizio 1
–
sezione nominale: S=25mm2
–
formazione : 7x2,14mm
–
diametro : d = 6,42mm
–
resistenza unitaria a 20°C: rl = 0,7199 Ω/km
elementi di linee elettriche: linee R-L
•
Una linea aerea in c.a. trifase lunga 5 km, funzionante a 50Hz, 10kV, trasmette
una potenza di 1000kW con cosϕ =0,9. La linea è costituita da conduttori di rame
a corda distanziati di 80cm e opera ad una temperatura di esercizio di 55°C.
Commercialmente è disponibile un conduttore di rame a corda con le seguenti
caratteristiche:
ammettendo una perdita di potenza del 5%
1. verificare se il cavo commercialmente disponibile è di sezione adeguata alle specifiche
di progetto
2. verificare se la perdita di potenza soddisfa la specifica data
3. calcolare il rendimento effettivo della linea
4. calcolare la caduta di tensione industriale in %
3.
– ESERCIZIO - 1
•
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
22
11
5B1
esercizio 1
esercizio 1: procedura di soluzione
•
si tratta del problema di progetto di una linea per la quale è fissata la perdita di
potenza ammissibile
•
il metodo di soluzione è pertanto basato sul criterio della perdita di potenza
ammissibile, ed essendo il sistema trifase, dovrà risultare
2
•
la procedura di soluzione prevede dunque i seguenti step
elementi di linee elettriche: linee R-L
– ESERCIZIO - 1
∆ p % = 3 Rl I ≅ 5 %
1. si calcola la sezione in funzione della perdita di potenza ammissibile fissata e se ne
verifica la compatibilità con il conduttore commercialmente disponibile
2. si calcola la ∆p% tenendo conto dei parametri del conduttore e delle specifiche di
progetto e si verifica che sia in accordo con la specifica data
3. nota la ∆p si calcola il rendimento
3.
4. si calcola infine la caduta di tensione industriale ∆V
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
23
5B1
esercizio 1
procedura di soluzione: step 1
•
si calcola la sezione in funzione della perdita di potenza ammissibile fissata e se ne verifica
la compatibilità con il conduttore commercialmente disponibile
•
essendo il sistema trifase, la sezione è data dalla relazione
∆ p %V 2 cos 2 ϕ
rl 20 = ρ 20
l
l
; rl55 = ρ 55
S
S
⇒
ρ 20 rl 20
=
ρ 55 rl55
ρ55 ovvero ρ a 55°C
⇒ ρ 55 = ρ 20 ⋅
rl 20 (1 + α ∆ T )
rl 20
elementi di linee elettriche: linee R-L
per conoscere il valore di S è necessario calcolare
= ρ 20 (1 + α ∆ T )
da cui la resistività a 55°C sarà
ρ 55 = ρ 20 (1 + α ∆ T ) = 0,0178 (1 + 0,00391 x 35 ) = 0,0202 Ω mm 2 m
e quindi la sezione
S=
100 ρ 55 LP
∆ p %V 2 cos 2 ϕ
=
100 x 0,0202 x 5000 x1000 x10 3
5(10 x10 3 ) 2 0,9 2
= 24 ,9 mm 2
che risulta quindi compatibile con quella del conduttore commerciale di sezione S=25 mm2
3.
– ESERCIZIO - 1
S=
100 ρ 55 LP
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
24
12
5B1
esercizio 1
procedura di soluzione: step 2
•
si calcola la ∆p% tenendo conto dei parametri del conduttore e delle specifiche di progetto e
si verifica che sia in accordo con la specifica data
•
essendo il sistema trifase, l’espressione della perdita di potenza ∆p è data dalla relazione
– ESERCIZIO - 1
∆ p = 3 Rl I 2
rl55 = ρ 55
elementi di linee elettriche: linee R-L
dove Rl=Lrl è calcolata alla temperatura di esercizio di 55 °C
ρ 55
1
0,0202
= rl 20
= 0,7199 x
= 0,819 Ω km ⇒ Rl = rl55 xL = 0,819 x 5 = 4,095 Ω
S
0,0178
ρ 20
per quanto riguarda I si ha
I =
P
3V cos ϕ
=
1000 x10
3
3 x10 x10 3 x 0,9
= 64 , 2 A
e quindi la potenza attiva effettivamente persa in linea vale
∆ p = 3 Rl I 2 = 3 x 4,095 x 64 , 2 2 = 50634 W
3.
che corrisponde ad un ∆p%=5,0634% in accordo quindi con la specifica data
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
25
5B1
esercizio 1
procedura di soluzione: step 3 e 4
•
nota la ∆p si calcola il rendimento
P
1000
η=
=
= 0,952
P + ∆ p 1000 + 50 ,6
si calcola infine la caduta di tensione industriale ∆V
è necessario a tale scopo calcolare xl; si ha
elementi di linee elettriche: linee R-L
2D
2 x 800
−3
−3
x l = ω ( 0, 4606 log
+ 0,064 )10 = 314 ( 0, 4606 log
+ 0,064 )10 = 0,367 Ω km
d
6, 42
la caduta di tensione industriale sarà quindi
∆V =
3 IL ( rl cos ϕ + x l sin ϕ ) =
3 x 64 ,3 x 5( 0,819 x 0,9 + 0,367 x 0, 436 ) = 515 V
e in valore percentuale
∆V
515 x100
∆V % =
100 =
= 5,15 %
V
10000
valore accettabile per l’impianto
3.
– ESERCIZIO - 1
•
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
26
13
5B1
esercizio 2
Una linea in c.a. monofase lunga 100 m, funzionante a 50Hz, 230V alimenta un
carico che assorbe una potenza di 25kW con un cosϕ =0,8 e un rendimento
uguale a 0,85. La linea è realizzata con cavo bipolare in rame, isolato in PVC,
posato entro un tubo in aria senza altri cavi vicini; la temperatura ambiente è di
35°C nelle condizioni più gravose.
•
Problema: scegliere il cavo più idoneo ipotizzando ∆V% ≤ 6% usando il metodo
della caduta di tensione unitaria
elementi di linee elettriche: linee R-L
•
3.
– ESERCIZIO - 2
esercizio 2
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
27
5B1
esercizio 2
esercizio 2: procedura di soluzione
si tratta del problema del calcolo di una linea con il criterio della massima caduta
di tensione ammissibile da risolvere con il metodo semplificato della caduta di
tensione unitaria definita dalla espressione
∆ V ⋅ 1000
u=
IL
la procedura di soluzione prevede i seguenti step
elementi di linee elettriche: linee R-L
•
1. si calcola la caduta di tensione ∆V = ∆V % V n/100
2. si calcola il valore della potenza assorbita dalla linea, della corrente I e quindi il valore
di u
3. si sceglie da tabella la sezione del cavo avente un valore di u minore di quello calcolato
4. si verifica tramite tabella se la portata è sufficiente; in caso contrario si sceglie il
conduttore con la sezione maggiore immediatamente successiva
3.
– ESERCIZIO - 2
•
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
28
14
5B1
esercizio 2
procedura di soluzione: step 1 e 2
1.
si calcola la caduta di tensione ∆V = ∆V % V n/100
∆ V % V n 5 x 230
∆V =
=
= 11,5 V
100
100
2.
si calcola il valore della potenza assorbita dalla linea, della corrente I e quindi il valore di u
– ESERCIZIO - 2
data la potenza assorbita dal carico e il suo rendimento, la potenza assorbita dalla linea sarà
PL
elementi di linee elettriche: linee R-L
25000
Pa =
=
= 29412 W
η
0,85
essendo il sistema monofase, la corrente vale
Pa
29412
I =
=
= 160 A
V n cos ϕ 230 x 0,8
e quindi
3.
1000 ∆ V 11 .5 x1000
mV
u=
=
= 0,719
IL
160 x100
Am
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
29
5B1
esercizio 2
procedura di soluzione: step 3 e 4
3.
si sceglie da tabella la sezione del cavo avente un valore di u minore di quello calcolato
dalla Tabella – 2 per i cavi bipolari con cosϕ=0,8 , si ha
si verifica tramite tabella se la portata è sufficiente; in caso contrario si sceglie il conduttore con la
sezione immediatamente successiva
elementi di linee elettriche: linee R-L
4.
S = 70 mm
2
dalla Tabella – 5 per i cavi bipolari in PVC da 70mm2, si ricava la portata di 175 A. Essendo poi la
temperatura di esercizio pari a 35°, dalla Tabella – 6 si ricava il coefficiente correttivo K1=0,77 e quindi la
portata effettiva vale
I z = 0,84 x175 = 147 A
essendo Iz<I il cavo scelto non è adatto ed è necessario quindi passare alla sezione successiva di
95mm2 per la quale la portata vale 208x0,84 = 174,72 A sensibilmente superiore alla corrente di impiego.
•
questo esempio mostra che l’alimentazione di carichi di elevata potenza con linee monofase
in bassa tensione è poco conveniente data la necessità di dover utilizzare dei conduttori di
elevata sezione !
3.
– ESERCIZIO - 2
mV
u = 0,624
;
Am
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
30
15
5B1
esercizio 3
esercizio 3
calcolo di progetto e verifica con il criterio della sovratemperatura
•
calcolare il diametro di un conduttore cilindrico in rame in grado di condurre una
corrente I=80A con una sopraelevazione di temperatura non superiore a 30°C
posto in un ambiente a temperatura di 40°C, con un coefficiente globale di
trasmissione, resistività e coefficiente di temperatura
– ESERCIZIO - 3
α 20 = 0,004 °C −1
ρ 20 = 0,0178 Ω mm 2 / m
λ = 15 W / m 2 K
2
ρ 20 = 0,0287 Ω mm / m
•
α 20 = 0,0038 °C
elementi di linee elettriche: linee R-L
verificare inoltre che un conduttore in alluminio, dello stesso diametro e nelle
stesse condizioni, sia in grado di condurre una corrente di 60A essendo resistività
e coefficiente di temperatura dell’alluminio a 20°C rispettivamente
−1
procedura di soluzione
1. si calcola la resistività a 70°C prima per il rame e poi per l’alluminio
2. si calcola il diametro e quindi la corrente, utilizzando l’equazione di equilibrio termico
per conduttori di sezione circolare
2
4 ρ I = λϑ π d
3
3.
∆
2
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
31
5B1
esercizio 3
esercizio 3
calcolo di progetto e verifica con il criterio della sovratemperatura
progetto
•
calcolo della resistività del rame a 70°
ρ 70 = ρ 20 (1 + α ∆ T ) = 0,0178 (1 + 0,004 ⋅ 50 ) = 0,0213 Ω ⋅ mm 2 m
calcolo del diametro
2
3
4 ρ I = λϑ π d ⇒ d =
3
4 ρI
∆
λϑ π
=
2
3
4 ⋅ 0,0213 ⋅ 10
−6
⋅ 80
2
= 0, 497 ⋅ 10 − 2 m ≅ 5 mm
2
15 ⋅ π ⋅ 30
elementi di linee elettriche: linee R-L
∆
2
2
verifica
•
calcolo della resistività dell’alluminio a 70°
ρ 70 = ρ 20 (1 + α ∆ T ) = 0,0287 (1 + 0,0038 x 50 ) = 0,034 Ω mm 2 m
•
calcolo della corrente
2
∆
2
3
4 ρ I = λϑ π d ⇒ I =
•
π
4
∆
λϑ d
ρ
3
= 1,571
15 x 30 x ( 0,5 x10
0,034 x10
6
−2 3
)
= 63 ,9 A
la verifica è positiva essendo I>60A
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
– ESERCIZIO - 3
•
a.s. 2015/2016
32
16
5B1
esercizio 4
esercizio 4
•
una barra rettangolare di alluminio posata in aria di dimensioni 25x4mm ,conduce
una corrente I=180A. Considerando una temperatura ambiente di 40°C e un
coefficiente di trasmissione λ=14W/(m2 K):
•
elementi di linee elettriche: linee R-L
– calcolare la corrente trasmissibile con una barra dello stesso materiale e della
stessa sezione,ma di forma circolare, funzionante nelle stesse condizioni
procedura di soluzione
1.
2.
3.
4.
5.
si calcola la resistività a 60°C dell’alluminio
si calcola la sovratemperatura
si calcola la temperatura di esercizio e si verifica la compatibilità con i dati del problema
si uguaglia la sezione della barra rettangolare ad una equivalente di sezione circolare
si calcola la corrente trasmissibile
3.
– ESERCIZIO - 4
– verificare che la temperatura di esercizio non superi i 60°C
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
33
5B1
esercizio 4
soluzione
1.
si calcola la resistività a 60°C dell’alluminio
ρ 60 = ρ 20 (1 + α ∆ T ) = 0,0284 (1 + 0,0038 ⋅ 40 ) = 0,0327 Ω ⋅ mm 2 m = 0,0327 x10 −6 Ω m
si calcola la calcola la sovratemperatura
dalla equazione dell’equilibrio termico
– ESERCIZIO - 4
essendo
Pc = RI
2
= ρ 60
ϑ∆
∆
Pc = λθ A
l 2
I ; S = bh;
S
A = 2 (b + h ) L ;
L
h = 4 mm
sostituendo si ottiene
∆
Pc = λθ A
⇒
ρ 60 LI
2
b = 25 mm
∆
= λθ 2 (b + h ) L
bh
elementi di linee elettriche: linee R-L
2.
barra rettangolare
da cui si ricava
ϑ
3.
∆
=
ρ 60 I 2
2 λ (b + h )bh
=
0,0327 x10 −6 x180 2
2 x14 ( 4 + 25 )10
−3
x 4 x10
−3
x 25 x10
−3
≅ 13 ,1 °C
si calcola la temperatura di esercizio
ϑ = ϑ a + ϑ ∆ = 40 + 13,1 = 53,1 °C < 60 °C
3.
che risulta quindi minore di 60°C come richiesto dal problema
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
34
17
5B1
esercizio 4
soluzione
4.
si uguaglia la sezione della barra rettangolare ad una equivalente di sezione circolare
per quanto riguarda le sezioni si ha
S R = bh
SC
2
d
= πr 2 = π
4
che uguagliate, consentono di calcolare il diametro della equivalente sezione circolare
d
⇒ bh = π
4
S R = SC
4bh
⇒d =
π
sostituendo i valori
d =
5.
4bh
π
=
4 x100
π
h = 4 mm
= 11,3mm
SC
SR
b = 25 mm
si calcola infine la corrente trasmissibile
elementi di linee elettriche: linee R-L
– ESERCIZIO - 4
2
d = 11,3mm
barra circolare
14 x13,1(11,3 x10 −3 ) 3
λϑ ∆ d 3
I = 1,571
= 1,571
= 141 A
−6
ρ
0,0329 x10
3.
da dove si vede che la sezione circolare ammette una portata minore rispetto a quella rettangolare
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
35
5B1
concepts …
si è visto che a parità di sezione e di tutte le altre condizioni, una barra di sezione circolare ammette una
portata minore di quella rettangolare
perché?
uguagliando le sezioni si ottiene
d2
bh = π
4
A P = 2 (b + h ) L
e
A C = 2πrL = πdL
4bh
→d =
elementi di linee elettriche: linee R-L
Calcolando e confrontando le superfici laterali si ha infatti
π
e la sezione circolare si può esprimere in funzione dei parametri di quella rettangolare nel seguente modo
AC = 2πrL = πdL = π
confrontando ora le due espressioni
π 2 bh
L=2
L = 2 πbh L
π
π
4bh
A P = 2 (b + h ) L
e
A P > AC
se
AC = 2 πbh L
si deduce che
(b + h ) > πbh
3.
– ESERCIZIO - 4
la risposta è semplice e risiede nel fatto che a parità di area di base e lunghezza, la superficie laterale
di un parallelepipedo è maggiore dei quella di un cilindro. Maggiore area laterale significa maggiore
superficie di scambio termico ed è quindi per questo che una barra di sezione rettangolare, a parità di
tutte le altre condizioni, ammette una portata maggiore.
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
36
18
5B1
concepts …
per dimostrare che a parità di area base e di lunghezza la superficie laterale AP di una barra a sezione rettangolare
(parallelepipedo) è maggiore di quella AC di una a sezione circolare (cilindro), si dovrà pertanto dimostrare che
(b + h ) > πbh
(1)
∀ b > 0, h > 0
trattandosi infatti delle dimensioni di una barra, non avrebbe senso b ≤ 0 e h ≤ 0e questo significa anche che il radicando
sarà sempre maggiore di zero. Elevando a quadrato primo e secondo membro si ha
→ b 2 + h 2 > πbh − 2bh
b 2 + h 2 > bh (π − 2 )
e quindi
→ b 2 + h 2 > bh (π − 2 )
(2)
elementi di linee elettriche: linee R-L
→ b 2 + h 2 + 2bh > πbh
la (2) non è che la (1) in una forma diversa e quindi la dimostrazione della (2) costituisce la dimostrazione della (1).
Considerando la (2), per quanto riguarda il secondo membro, vale la relazione
ma, nel quadrato di un binomio, si dimostra che è sempre
per cui a maggior ragione sarà
b 2 + h 2 > bh (π − 2 )
2bh > bh (π − 2 )
b 2 + h 2 ≥ 2bh
c.v.d.!
nel caso del problema in esame, considerando una lunghezza unitaria, si ha per esempio
A P = 2 ( 25 + 4 ) = 58 mm 2
AC = 11 .3π = 35 ,5 mm 2
3.
da cui emerge con evidenza la maggiore superficie laterale della barra a sezione rettangolare rispetto a quella circolare
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
37
5B1
4-BP
Cadute di tensione in mV/(A m) per cavi BT unipolari (da norma CEI-UNEL 35023) – Tabella 1
Cadute di tensione in mV/(A m) per cavi BT bipolari e tripolari (da norma CEI-UNEL 35023) –
Tabella 2
elementi di linee elettriche: linee R-L
Valori della portata I0 di cavi unipolari e multipolari per bassa tensione isolati
in PVC ed EPR (o XLPE), per le diverse condizioni di posa (da norma CEI-UNEL 35026)
A. Cavi unipolari in tubi interrati tra loro a contatto (1 cavo per tubo) – Tabella 3
B. Cavi unipolari in un unico tubo interrato – Tabella 4
C. Cavo multipolare in tubo interrato– Tabella 5
Valori del fattore di correzione k1 per temperature del terreno diverse da 20 °C (da norma CEIUNEL 35026) – Tabella 6
Valori del fattore di correzione k2 per gruppi di più circuiti (cavi unipolari) o
di più cavi multipolari installati sullo stesso piano (da norma CEI-UNEL 35026) – Tabella 7
tabelle
Valori del fattore di correzione k3 per differenti valori della profondità di posa (da norma CEIUNEL 35026) – Tabella 8
Valori del fattore di correzione k4 per differenti valori della resistività termica del terreno (da
norma CEI-UNEL 35026) – Tabella 9
Valori medi della resistività termica di alcuni tipi di terreno e di materiali – Tabella 10
3.
– ESERCIZIO - 4
(b + h ) 2 > πbh
impianti elettrici
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
2015/2016
a.s. 2012/2013
38
19
5B1
3.
elementi di linee elettriche: linee R-L
Non è possibile v isualizzare l'immagine.
Tabella 1
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
39
5B1
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
elementi di linee elettriche: linee R-L
Non è possibile v isualizzare l'immagine.
Tabella 2
a.s. 2015/2016
40
20
TPS
3.
elementi di linee elettriche: linee R-L
5B1
Tabella 3
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
41
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
elementi di linee elettriche: linee R-L
5B1
Tabella 4
a.s. 2015/2016
42
21
3.
elementi di linee elettriche: linee R-L
5B1
Tabella 5
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
43
5B1
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
elementi di linee elettriche: linee R-L
Non è possibile v isualizzare l'immagine.
Tabella 6
a.s. 2015/2016
44
22
5B1
elementi di linee elettriche: linee R-L
Non è possibile v isualizzare l'immagine.
3.
Tabella 7
Tabella 8
TPS
a.s. 2015/2016
L. Agarossi - ITIS “P. Hensemberger - Monza -
45
5B1
Non è possibile v isualizzare l'immagine.
L. Agarossi - ITIS “P. Hensemberger - Monza -
3.
TPS
elementi di linee elettriche: linee R-L
Tabella 9
Tabella 10
a.s. 2015/2016
46
23
5B1
concepts…
valore efficace o RMS (Root Mean Square)
•
il valore efficace di una grandezza sinusoidale equivale a quel valore che
tale grandezza dovrebbe possedere in continua per erogare nello stesso
intervallo di tempo la stessa potenza
•
per i segnali sinusoidali vale la seguente relazione
elementi di linee elettriche: linee R-L
Yeff =
YM
1 T 2
2
=
= 0.707 YM
Y
sin
ω
t
dt
∫
T 0
2
M
y(t)
YM
YM
Yeff =
2
YM
2
t
3.
T
TPS
L. Agarossi - ITIS “P. Hensemberger - Monza -
a.s. 2015/2016
47
24