Fluidi
Una sostanza che non ha delle dimensioni definite, ma che prende la forma
del contenitore entro la quale e’ confinata, prende il nome di fluido.
In base a tale definizione, sia i gas che i liquidi sono dei fluidi.
Una distinzione fra liquidi e gas puo’ essere basata sulla osservazione che una
certa quantita’ di liquido ha un volume definito, mentre un gas si espande fino
a riempire completamente il recipiente in cui e’ posto. Questo differente
comportamento macroscopico dipende dalle differenti proprieta’ delle forze di
coesione fra le molecole.
Pressione
Immaginiamo di immergere in un fluido un sensore
molto piccolo, come quello schematizzato in figura.
Un pistone avente area A e massa trascurabile puo’
scorrere, vincolato ad una molla, in un cilindro
all’interno del quale e’ fatto il vuoto. Quando lo
strumento viene immerso, il fluido esercita sul pistone
una forza di modulo F, perpendicolare al pistone
stesso, spingendolo verso l’interno. Il pistone
raggiungera’ la posizione in cui la forza esercitata
dalla molla su di esso bilancia quella esercitata dal
fluido.
Definiamo pressione P del fluido nel punto in cui si trova il sensore lo
scalare dato dal rapporto
P= F/A
Si trova sperimentalmente che la pressione P cosi’ definita non dipende
dall’orientamento del sensore.
La unita’ di misura della pressione nel S.I. e il Pascal (Pa)
1 Pa = 1 N/m2
Altre unita’ di misura della pressione ancora utilizzate sono:
l’atmosfera (atm) equivalente alla pressione media della atmosfera a livello
del mare; il torr equivalente alla pressione esercitata da una colonna di 1 mm
di mercurio ed il bar equivalente a 105 Pa
1Atm=1.01 105 Pa = 1.01 bar = 760 torr
Massa volumica
La massa volumica ρ (o densita’) di una sostanza e’ definita come la
massa per unita’ di volume della sostanza considerata.
Poiche’ come osservato i gas non hanno un volume definito, la loro massa
volumica dipendera’ fortemente dalla pressione e dalla temperatura.
Tale dipendenza e’ invece solitamente trascurabile o molto debole per i
liquidi ed i solidi
Esempio 1
Una stanza ha un pavimento di dimensioni 3.5 m per 4.5 m ed altezza di 3.2 m.
Calcolare la massa m ed il peso mg dell’aria contenuta nella stanza a pressione
atmosferica e temperatura di 0o C ed il modulo F della forza esercitata
dall’aria sul pavimento della stanza.
m = ρ V = 1.29 (3.5 x 4.5 x 3.2) = 65 kg
mg = 6.4 102 N
F = PA= 1.01 105 x (3.5 x4.5) = 1.6 106 N
Tale enorme forza e’ equivalente al peso di una massa di
1.6 105 kg ! !
Legge di Stevino
Ci proponiamo di capire in che modo varia con la profondita’
la pressione di un fluido in quiete avente densita’ ρ costante.
Consideriamo un contenitore contenente un liquido in quiete avente densita’
ρ come schematizzato in figura.
y
Consideriamo la quantita’ di liquido contenuta dentro un cilindro immaginario
avente base di area A e che si estende dalla superficie fino alla profondita’ h.
Sia P la pressione esercitata dal liquido esterno al cilindro sulla base del
cilindro a profondita’ h. La pressione esercitata dall’aria sulla superficie del
cilindro e’ la pressione atmosferica P0. Poiche’ il cilindro di liquido e’ in
quiete, la componente rispetto all’asse y della risultante delle forze agenti sul
cilindro deve essere nulla. Quindi si ha:
+P0A +Mg – PA = 0 ⇒ + P0A +(A h ρ )g – PA = 0 ⇒
P= P0 + ρ g h
Cioe’ la pressione ad una profondita’ y=h e’ maggiore della pressione
atmosferica di una quantita’ ρ g h
Tale legge prende il nome di legge di Stevino.
Esempio 2: il barometro a mercurio
Evangelista Torricelli (1608-1647), al quale e’ dedicato il nome di una delle
unita di misura della pressione, il torr, invento’ un semplice strumento che
consente di misurare la pressione atmosferica: il barometro a mercurio.
y
Il barometro e’ costituito da un tubo, chiuso ad una estremita’, riempito di
mercurio. Il tubo viene rovesciato in un contenitore aperto, anch’esso pieno di
mercurio, avendo cura di non fare entrare aria nel tubo stesso durante la
operazione. Alla estremita’ chiusa del tubo si crea una zona di ‘vuoto’ dove la
pressione puo’ essere considerata nulla. La altezza della colonna di mercurio
osservata eseguendo l’ esperimento al livello del mare e’ di 76 cm.
Dalla legge di Stevino abbiamo che
P0 = P+ ρ gh = 0 + ρ gh = ρ gh = 1.01 105 Pa = 1 atm
La pressione atmosferica e’ quindi equivalente a quella generata da una
colonna di mercurio di altezza h=76 cm
Principio di Pascal
Come abbiamo visto, la pressione in un fluido in quiete dipende solo dalla
profondita’. Pertanto, ad esempio, un aumento della pressione P0 sulla
superficie sara’ trasmesso in qualsiasi altro punto del fluido. Il primo a
comprendere cio’ fu Blaise Pascal (1623-1662), al quale e’ dedicato il nome
della unita’ di pressione del S.I., che enuncio’ la legge oggi nota come
principio di Pascal:
Una variazione di pressione applicata ad un fluido viene trasmessa invariata
ad ogni punto del fluido e alle pareti del contenitore.
Esempio 3: un sollevatore per auto
Una importante applicazione del principio di Pascal e’ il martinetto idraulico
la cui logica di funzionamento e’ la seguente.
Una forza F1 viene applicata ad un piccolo pistone di area A1. La pressione
viene trasmessa attraverso un fluido ad un pistone di area A2>A1,
sul quale sara’ quindi esercitata una forza F2.
Poiche’ la pressione e’ la stessa su entrambi i pistoni si ha:
P = F1/A1 = F2 / A2 ⇒ F2 = F1 (A2/A1) > F1
Su tale principio si basa il funzionamento di freni idraulici,
sollevatori idraulici, carrelli elevatori e simili.
y
Un elevatore tiene sollevata una automobile di massa M=1.3 103 kg. Per fare
funzionare l’elevatore si utilizza dell’aria compressa per comprimere un
pistoncino di raggio R1=5.0 cm, mentre il raggio del secondo pistone e’
R2=15 cm. Quale forza F1 deve esercitare l’aria compressa per tenere
sollevata l’auto? Quale sara’ la pressione dell’aria compressa necessaria?
Mg + F2 = ma = 0 ⇒ -Mg + F2 = 0 ⇒ - Mg + F1 (A2/A1) =0 ⇒
⇒F1= Mg (A1/A2) = Mg (R1/R2)2 = (1/9) Mg= 1.4 103 N
P = F1/A1 = F1/(π R12) = 1.8 105 Pa = 1.8 atm
Principio di Archimede
Archimede, piu di 2000 anni addietro, enuncio’
quello che e’ oggi noto come
principio di Archimede:
un corpo immerso in un fluido riceve una spinta dal
basso verso l’alto pari al peso del fluido spostato.
Ci proponiamo di capire, alla luce delle nostre
conoscenze attuali, quale e’ l’origine di tale spinta.
y
Dato un contenitore contenente un fluido in quiete
avente densita’ ρ , consideriamo la quantita’ di fluido
contenuta dentro un cubo immaginario di lato L come
schematizzato in figura. Poiche’ il cubo di fluido e’ in
quiete, la componente lungo l’asse y della risultante delle
forze agenti sul cubo di fluido deve essere nulla. Quindi:
-Fg + B = 0 ⇒ B = Fg = mg
Quindi la spinta B verso l’alto agente sul cubetto di fluido e’ uguale, in
modulo, al peso del cubetto di fluido stesso.
Ora se il cubetto di fluido venisse sostituito da da un cubetto di un’altra
sostanza,avente le stesse dimensioni, il fluido circostante si comporterebbe
allo stesso modo e la spinta rimarrebbe uguale al peso del fluido spostato.
Notiamo che la spinta di Archimede e’ originata dalla differenza di pressione
∆P = Pdown - Pup fra la faccia inferiore (down) e superiore (up) del cubo.
B = Fdown– Fup = L2 Pdown - L2 Pup = L2 (Pdown - Pup ) =
L2 (ρ gL) = (L3 ρ ) g = mg
Condizione di galleggiamento
Cosa succede ad un corpo di densita’ ρ c quando viene immerso in un fluido
di densita’ ρ f ? Come conseguenza del principio di Archimede si ha che:
se ρ c < ρ f il corpo sara’ soggetto ad una forza risultante rivolta verso l’alto
e galleggera’ nel fluido,
se ρ c > ρ f il corpo sara’ soggetto ad una forza risultante rivolta verso il
basso ed affondera’ nel fluido.
Infatti, detto Vc il volume del corpo considerato, la componente della forza
risultante F rispetto ad un asse verticale rivolto verso l’alto sara’:
Fy=-mg + Vc ρ f g =-Vc ρ c g + Vc ρ f g =Vcg(ρ f - ρ c)
Essa sara’ quindi positiva se ρ c < ρ f e negativa se ρ c > ρ
f.
Esempio 4: il galleggiamento di un iceberg
Dato un iceberg, che galleggia in mare aperto, ci proponiamo di calcolare
quale e’ la frazione del suo volume che rimane immersa sapendo che:
la densita’ del ghiaccio costituente l’iceberg e’ ρ i = 917 kg/m3 e
la densita’ dell’acqua dove esso e’ immerso e’ ρ f = 1030 kg/m3.
La parte immersa dell’iceberg deve generare una spinta di Archimede B pari
in modulo al peso Pi dell’iceberg stesso. Pertanto, detti Vi il volume totale
dell’iceberg e V il volume della sua parte immersa si ha:
Pi = B ⇒ Vi ρ i g = V ρ f g ⇒ V/ Vi = ρ i / ρ f = 0.89 = 89 %
Da cui il modo di dire “ e’ solo la punta di un iceberg” !
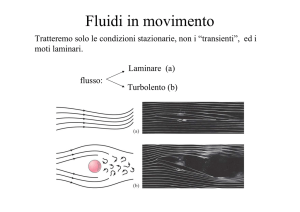
Introduzione alla dinamica dei fluidi:
moto di un fluido ideale
Finora ci siamo limitati allo studio di un fluido in quiete. Lo studio del
moto di un fluido reale e’ molto complesso, pertanto ci limiteremo ad
introdurre alcune nozioni basilari riguardanti lo studio del moto di un
fluido ideale.
Lo studio del moto di un fluido ideale e’ basato sulle seguenti ipotesi.
Il fluido non e’ viscoso
La viscosita’ e’ per i fluidi l’analogo dell’attrito per i solidi. Essa
rappresenta una sorta di attrito interno fra le varie particelle del fluido e fra
il fluido e le pareti della condotta. Ad esempio, dalla definizione data,
segue che un oggetto in moto all’interno di un fluido non viscoso non
sarebbe soggetto ad alcuna forza che si oppone al suo moto.
Analogamente all’effetto delle forze di attrito nel moto dei solidi, nel
moto di un fluido viscoso della energia meccanica viene trasformata in
energia termica.
Il fluido e’ incomprimibile.
Assumiamo cioe’ che la massa volumica (densita’) del fluido sia costante.
Essa sara’ quindi la stessa in qualsiasi punto all’interno della condotta.
Il moto e’ stazionario.
Il moto e’ stazionario quando, considerato un punto generico all’interno
della condotta, la il vettore velocita’ delle particelle di fluido che transitano
in quel punto non cambia col tempo.
Il moto e’ irrotazionale.
Il moto di un fluido e’ irrotazionale se nessuna delle sue particelle ruota
attorno ad un asse passante per il suo centro di massa. Ad esempio
immaginiamo di far muovere un piccolo granello di polvere in un fluido. Se
il moto e’ irrotazionale, il granello di polvere non ruoterebbe attorno ad un
asse passante per il suo centro di massa anche se dovesse muoversi lungo
un camino circolare.
Equazione di continuita’
Consideriamo un fluido
ideale che si muova
lungo una condotta
di sezione variabile
come schematizzato in
figura.
La massa m1 di fluido che attraversa la sezione A1 in un intervallo di tempo t
deve essere uguale alla massa m2 che attraversa la sezione A2 nello stesso
intervallo di tempo. Pertanto:
m1 = m2 ⇒ ρ 1(A1∆x1 ) = ρ 2 (A2∆x2) ⇒
⇒ ρ 1(A1v1 t) = ρ 2 (A2v2 t) ⇒
⇒ ρ 1 A1 v1 = ρ 2 A2v2 ⇒
⇒(se la densita’ e’ costante) A1v1 = A2v2
Tale equazione prende il nome di equazione di continuita’
e mostra che la velocita’ del fluido e’ maggiore dove il tubo e’ piu’ stretto e
minore dove il tubo e’ piu’ largo. Il prodotto AV, che ha le dimensioni di un
volume diviso un tempo, e’ chiamato portata.
Esempio 5
A1
Osservando un flusso di acqua che esce da
un rubinetto, notiamo che la sua sezione si
restringe (A2 < A1 ) man mano che l’acqua
cade acquistando velocita’. Cio’ e’ una
diretta conseguenza della equazione di
continuita’. Infatti:
A1v1 = A2 v2
ma
v2>v1
quindi
A2
A2<A1
Equazione di Bernoulli
Daniel Bernoulli ricavo’ per primo la seguente equazione che, per il moto
di un fluido ideale di densita’ ρ , lega la pressione P, la velocita’ v e la quota
y del fluido dentro la condotta dove esso scorre:
P1 + 1/2 ρ v12 + ρ gy1 = P2 + 1/2 ρ v22 + ρ gy2 = costante
Tale equazione, ricavata tramite considerazioni di tipo energetico, e’ oggi
nota come equazione di Bernoulli.
Ci proponiamo ora di dimostrare la suddetta equazione.
Prendiamo in considerazione la quantita’ di fluido (avente volume V e massa
m = V ρ ) che in un tempo t attraversa le sezioni 1 e 2 della condotta . Poiche’
stiamo ipotizzando che il moto del fluido sia ideale (e quindi stazionario), la
porzione di fluido compresa fra ∆x1 e ∆x2 non subisce alcuna variazione nel
tempo t. Quindi, dal punto di vista energetico, e’ come se nel tempo t la
massa m di fluido considerata si spostasse dal tratto ∆x1 al tratto ∆x2.
Il fluido a sinistra della sezione 1 effettua sulla massa m di fluido
considerata un lavoro L1
L1 = F1 ∆ x1 = P1A1 ∆x1 = P1 V
Analogamente il fluido a destra della sezione 2 effettua su m un lavoro
L2 = - F2 ∆x2 = - P2A2 ∆x2 = - P2 V
Imponendo che lavoro totale sia uguale alla variazione di energia meccanica
totale della massa m di fluido considerata, otteniamo la equazione di Bernoulli
Ltot = L1 + L2 = (P1-P2) V
Ltot = ∆K + ∆U
(P1-P2) V = (1/2mv22 - 1/2 m v12) + (mgy2-mgy1)
(P1-P2) = (1/2 ρ v22 - 1/2 ρ v12) + (ρ gy2- ρ gy1)
P1 + 1/2 ρ v12 + ρ gy1 = P2 + 1/2 ρ v22 + ρ gy2
Esempio 6
Un serbatoio di acqua ha su una parete un forellino di diametro trascurabile
rispetto al diametro del serbatoio stesso. Il foro si trova ad una quota h al di
sotto del livello dell’acqua nel serbatoio. Con quale velocita’ l’acqua esce dal
forellino?
Siano ‘A’ ed ‘a’ le sezioni del serbatoio e del forellino; ‘V’ e ‘v’ le velocita’
dell’acqua alla superficie del serbatoio e all’uscita dal forellino. Siano inoltre
P0 la pressione atmosferica e ρ f la densita’ dell’acqua.
Dalla equazione di continuita’ si ha:
A V = a v ⇒ V= v (a/A)
Ma a<<A ⇒ V<<v
Applicando l’equazione di Bernoulli si ottiene:
P0 + ½ ρ f V2 + ρ f gh = P0 + ½ ρ f v2 + 0
Poiche’ V<<v
+ ½ v2 = ½ V2 + gh
il termine 1/2 V2 sara’ trascurabile rispetto ½
+ ½ v2 = gh ⇒ v = [2gh]1/2
v2 e si avra’
L’acqua avra’ quindi la stessa velocita’ che avrebbe un corpo
cadendo da una quota h
Esempio 7: il tubo di venturi
Il tubo di venturi e’ uno strumento che puo’ misurare la velocita’ di un fluido
in una conduttura, se inserito nella conduttura stessa. Esso e’
essenzialmente un tubo avente gli estremi della stessa sezione ‘A’ della
conduttura in cui e’ inserito e il centro di sezione ‘a’ minore. Un
manometro consente di misurare la differenza di pressione P1-P2>0 fra un
estremo dello strumento ed il centro. Abbiamo che:
•
Equazione di Bernoulli ⇒ P1+ 1/2ρ v12 =P2 +1/2 ρ v22
2) Legge di Stevino ⇒ P1-P2= ρ gh misurabile
3)Equazione di continuita ⇒ Av1=av2
Utilizzando le 3 equazioni
suddette e’ possibile
esprimere la velocita’ v1
del fluido in funzione della
differenza di pressione
ρ gh misurata.
Esempio 8: cosa genera la portanza negli aerei ?
La spinta che agisce sulle ali degli aerei e’, in parte, una diretta conseguenza
della equazione di Bernoulli. La forma dell’ala e’ tale che la velocita’ dell’aria
che scorre sulla parte superiore dell’ala sia maggiore di quella dell’aria che
scorre lungo la parte inferiore. Pertanto, come predetto dalla equazione di
Bernoulli, la pressione sara’ inferiore sopra l’ala e la forza risultante agente
sara’ rivolta verso l’alto.
Un altro effetto che contribuisce a generare la
portanza e’ il seguente. L’ala ha una lieve
angolazione verso l’alto, per cui le molecole
d’aria che colpiscono la parte inferiore
vengono deviate verso il basso. Cio’ significa
che: l’ala esercita sulle molecole d’aria una
forza diretta verso il basso, quindi, per la III
legge di Newton, l’aria esercitera’ una forza
sull’ala diretta verso l’alto.
Esempio 9:
la equazione di Bernoulli ed… i tiri di Platini’ …
Abbiamo piu’ volte detto che un corpo, lanciato con velocita’ diversa da
zero in prossimita’ della superficie terrestre, si muovera’ su un piano lungo
una traiettoria parabolica. Sappiamo pero’ che in alcuni sport come il calcio,
il pingpong, il tennis, dei bravi giocatori riescono a far si che una palla
segua delle traiettorie che si discostano di molto da una parabola…
Non dobbiamo dimenticare che, nel dimostrare che la traiettoria deve
essere parabolica, abbiamo trascurato la interazione con l’aria che e’, in
realta’, un fluido reale! Traiettorie particolari possono essere ottenute
tirando la palla in modo che essa abbia una grande velocita’ angolare
attorno ad un asse passante per il suo centro. Consideriamo la figura in
basso. Se in un dato istante la velocita’ di traslazione del pallone ha direzione
e verso della linea tratteggiata, la velocita’ dell’aria rispetto al pallone avra’
verso opposto. Inoltre, se la palla ruota in senso antiorario, essa ‘trascinera’
con se un sottile strato di aria che tendera’ a ruotare con essa.
La velocita’ dell’aria rispetto al pallone sara’
data dalla somma della velocita’ dell’aria
legata alla traslazione e di quella legata alla
rotazione. Nell’esempio in figura tali velocita’
hanno verso concorde alla sinistra del pallone
e opposto alla destra. La velocita’ dell’aria
rispetto al pallone sara’ quindi maggiore alla
sinistra del pallone e, come conseguenza della
equazione di Bernoulli, la pressione sara’
inferiore. Il pallone sara’ quindi soggetto ad
una forza rivolta’ verso sinistra che fara’ si che
la sua traiettoria non sia parabolica.
Alcuni quesiti di verifica
1)Sapreste discutere il principio di funzionamento di un barometro al
mercurio? Se si volesse costruire uno strumento di questo tipo utilizzando
acqua al posto del mercurio, quale altezza della colonna di acqua vi
aspettereste?
2)Conoscete ed avete capito il significato della legge di Stevino del
principio di Pascal e del principio di Archimede?
3)Quali sono le condizioni che devono essere soddisfatte affinche’ un corpo
possa galleggiare in un fluido?
4)Sotto quali condizioni e’ valida la equazione di Bernoulli ?
5)La equazione di Bernoulli e’ in qualche modo legata ad un principio di
conservazione? Discutere.
6)Sapreste mettere in relazione qualche fenomeno osservabile
comunemente, con la equazione di Bernoulli e/o con la equazione di
continuita’ ?