Contresempi inerenti i criteri di congruenza dei triangoli
Il primo criterio di congruenza dei triangoli afferma che: “Due triangoli sono
congruenti se hanno ordinatamente congruenti due lati e l’angolo compreso tra i lati”.
Ma è proprio indispensabile che quest’angolo sia compreso tra i lati?
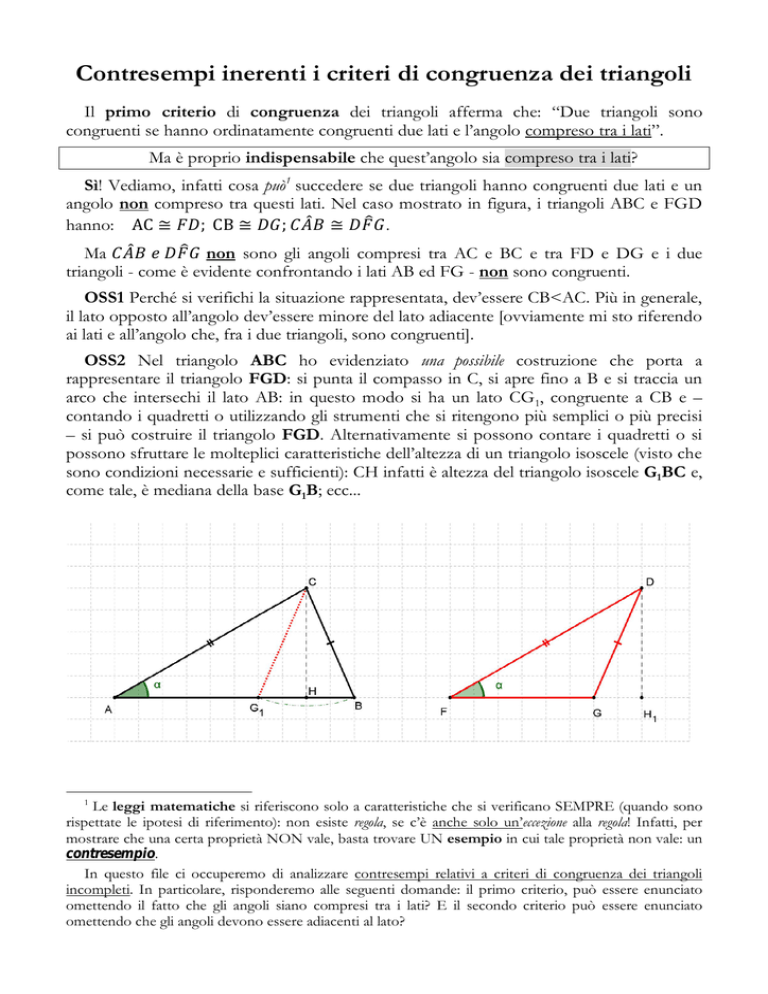
Sì! Vediamo, infatti cosa può1 succedere se due triangoli hanno congruenti due lati e un
angolo non compreso tra questi lati. Nel caso mostrato in figura, i triangoli ABC e FGD
hanno: AC ≅
; CB ≅
;
≅
.
Ma
non sono gli angoli compresi tra AC e BC e tra FD e DG e i due
triangoli - come è evidente confrontando i lati AB ed FG - non sono congruenti.
OSS1 Perché si verifichi la situazione rappresentata, dev’essere CB<AC. Più in generale,
il lato opposto all’angolo dev’essere minore del lato adiacente [ovviamente mi sto riferendo
ai lati e all’angolo che, fra i due triangoli, sono congruenti].
OSS2 Nel triangolo ABC ho evidenziato una possibile costruzione che porta a
rappresentare il triangolo FGD: si punta il compasso in C, si apre fino a B e si traccia un
arco che intersechi il lato AB: in questo modo si ha un lato CG1, congruente a CB e –
contando i quadretti o utilizzando gli strumenti che si ritengono più semplici o più precisi
– si può costruire il triangolo FGD. Alternativamente si possono contare i quadretti o si
possono sfruttare le molteplici caratteristiche dell’altezza di un triangolo isoscele (visto che
sono condizioni necessarie e sufficienti): CH infatti è altezza del triangolo isoscele G1BC e,
come tale, è mediana della base G1B; ecc...
1
Le leggi matematiche si riferiscono solo a caratteristiche che si verificano SEMPRE (quando sono
rispettate le ipotesi di riferimento): non esiste regola, se c’è anche solo un’eccezione alla regola! Infatti, per
mostrare che una certa proprietà NON vale, basta trovare UN esempio in cui tale proprietà non vale: un
contresempio.
In questo file ci occuperemo di analizzare contresempi relativi a criteri di congruenza dei triangoli
incompleti. In particolare, risponderemo alle seguenti domande: il primo criterio, può essere enunciato
omettendo il fatto che gli angoli siano compresi tra i lati? E il secondo criterio può essere enunciato
omettendo che gli angoli devono essere adiacenti al lato?
Il secondo criterio di congruenza dei triangoli afferma che: “Due triangoli sono
congruenti se hanno ordinatamente congruenti un lato e gli angoli adiacenti al lato”.
Ma è proprio indispensabile che questi angoli siano adiacenti al lato?
Sì! Vediamo, infatti cosa può succedere
se due triangoli hanno congruenti un lato
e angoli non adiacenti a questo lato. Nel
caso mostrato in figura, i triangoli ABC e
DEF, entrambi rettangoli2, hanno:
AB ≅
;
≅
;
≅
.
Ma gli angoli congruenti non sono
quelli adiacenti al lato congruente e i due
triangoli non sono congruenti - come è
evidente ricordando che, in un triangolo
rettangolo, l’ipotenusa è il lato maggiore
e considerando che l’ipotenusa di ABC è
congruente a un cateto di EFD.
OSS1 In figura sono date le misure
delle ampiezze degli angoli e delle
lunghezze dei lati, per convincere chi legge.
OSS2 Quel che conta è costruire triangoli
simili3 (ma non congruenti4), perché vogliamo
che abbiano gli angoli congruenti. Come fare a
costruire triangoli simili? Utilizzando la
definizione, contando i quadretti e osservando
quanto rappresentato in figura.
Infatti, dato un triangolo rettangolo ACD e
tracciata l’altezza CE relativa all’ipotenusa
AD, i tre triangoli ACD (grosso), CEA (medio),
DEC (piccolo), sono tutti simili tra loro. Infatti, se α è la misura dell’ampiezza dell’angolo in A,
e 90° è la misura dell’ampiezza dell’angolo in C, l’angolo in D misura 90°- α (fai la prova:
A+B+C=180°). Ma, con ragionamento analogo, anche ECA=90°- α e, quindi, ECD= α. E
si può dimostrare come questa caratteristica sia una CNS per avere un triangolo rettangolo.
Stabilito ciò, osserva come il rapporto fra cateto minore e cateto maggiore del triangolo
EDF della fig.1 sia ½ . ABC è simile a EDF perché il rapporto tra i cateti dei triangoli
CHA e BHC è sempre ½! Prova, riprova e riprova, per convincertene...
2 Ho scelto triangoli rettangoli per semplificarne il disegno. Questo particolare non indebolisce il contresempio
perché, come già detto, un esempio qualunque va bene per dimostrare che una proposizione non è vera (in questo
caso, la proposizione: “Due triangoli sono congruenti se hanno congruenti ordinatamente un lato e due angoli”).
3 DEF Due figure si dicono simili se hanno i lati ordinatamente in proporzione. In particolare, solo per i
triangoli [CONTRES: pensa ai rettangoli], vale il seguente criterio di similitudine: “Due triangoli sono simili se
hanno gli angoli congruenti”.
4 La relazione di congruenza è un caso particolare della relazione di similitudine: il caso in cui il rapporto di
proporzionalità è 1!












