Il frattale di Mandelbrot

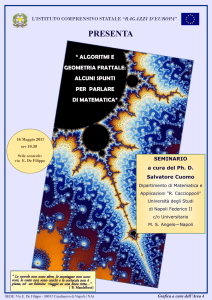
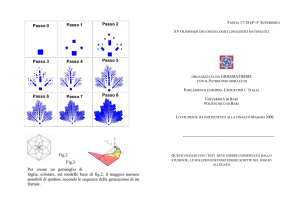
Il frattale di Mandelbrot
a cura di Flavio Cimolin
(formula suggerita da Andrea Zanni)
(ultimo aggiornamento: 22/10/2005)
I frattali sono fra tutti gli oggetti matematici quelli che più
impressionano anche chi di matematica non capisce
assolutamente nulla. Si parte da una figura come quella qui
a fianco (che è una rappresentazione dell'insieme di
Mandelbrot, il frattale forse più famoso), e poi ci si
abbandona nell'osservare le linee e i colori, alla ricerca di
schemi che si ripetono sempre, ma su scale diverse.
L'occhio è alla continua ricerca del confine della figura, ma
non lo può trovare, perchè esso non esiste: se si ingrandisce
l'immagine si scoprono sempre nuove insenature, sempre
diverse ma sempre simili a quella iniziale. E' questa
indefinitezza
e
autosomiglianza
che
definisce
concettualmente quello che è un frattale.
Ma cosa c'entra in questo discorso la matematica? C'entra eccome, perché i frattali sono degli
oggetti matematici veri e propri, definiti in una maniera rigorosa attraverso delle formule. Lo studio
della geometria frattale è tutto sommato abbastanza recente, ed inizia con Mandelbrot e Julia verso
l'inizio del ventesimo secolo. Solo la potenza di calcolo fornita negli ultimi anni dall'avvento dei
computer è però riuscita a mostrarci in tutti i loro dettagli questi straordinari oggetti. Le immagini
che vediamo, infatti, sono solo una rappresentazione degli insiemi frattali, in cui ad ogni numero
viene associato un colore.
Ma il bello deve ancora venire! Infatti nonostante si possa pensare che un oggetto così complicato
come un frattale necessiti di una formula particolarmente lunga e complessa per essere descritto,
nulla è più lontano dal vero. Che ci crediate o no, la formula con cui viene generato l'insieme di
Mandelbrot è la seguente:
Si tratta semplicemente di quella che in analisi matematica è una parabola traslata rispetto
all'origine di un termine noto c! L'incognita è indicata con z perché questa è la lettera che
usualmente i matematici usano per i numeri complessi. Il frattale di Mandelbrot è infatti definito in
un piano semicomplesso (due assi sono per la parte reale ed immaginaria dei numeri, e la
rappresentazione avviene grazie all'uso di colori diversi). Il modo di procedere può essere molto
brevemente descritto nel modo seguente: per ogni punto X del piano complesso, si pone c = X, e
poi, a partire da z = 0 + i*0, si calcola iterativamente Z con la formula descritta sopra, fino a
quando il suo modulo sqr(Re[Z]^2 + Im[z]^2) diventa maggiore di un certo valore G, che non è
http://www.matematicamente.it
Flavio Cimolin – Il frattale di Mandelbrot
altro che la grandezza del quadrato all'interno del quale vogliamo rappresentare il frattale. Il numero
di volte che bisogna iterare il procedimento prima di fermarsi è proprio il valore che associamo al
punto scelto X, che quindi coloriamo in base ad una scala precedentemente definita (la ripetizione
infinite volte è un colore!). Seguendo rigorosamente lo schema, grazie alla semplicissima formula
Z=z*z+c, si crea un oggetto estremamente bello e complesso, che è proprio il frattale di
Mandelbrot.
Giusto per meravigliarsi ancora un po', qui sotto ci sono quattro zoom progressivi di una zona
chiamata "Sea Horse" (Cavalluccio Marino), attraverso i quali si possono intuire ancora una volta
quelle che sono le proprietà fondamentali dei frattali: l'autosomiglianza su scale diverse, e
l'indefinitezza del confine.
A titolo di curiosità, infine, se si invertissero i ruoli di z e c, ovvero fissato un generico c, per ogni
punto X scelto si ponesse z = X e poi si iterasse il procedimento come sopra, si otterrebbe un altro
insieme frattale molto noto: il frattale di Julia.
2
http://www.matematicamente.it