FISICA a.a. 2009-2010
Prof. G. Della Valle
Moto in un campo di forze centrali
1. Moto in un campo di forze centrali
Planarità del moto
In un campo di forze
! centrali avremo sempre:
! ! !
!
! !
dL
F (r )|| r !
= r " F = 0 ! L = cost.
dt
e quindi il moto è piano.
Si tratta di una delle caratteristiche principali dei campi di forze centrali. Più precisamente, in
un campo di forze centrali, il momento angolare rispetto al centro di forza O si conserva.
Nota bene: non è vera, in generale, l’implicazione inversa. Se infatti il momento angolare è
costante, avremo certamente che il momento della forza risultante si annulla, ma ciò può
corrispondere a due situazioni differenti:
! ! !
a) F (r )|| r ! il punto materiale P si muove effettivamente in un campo di forze centrali
di centro O.
b) il punto materiale P non è soggetto ad alcuna interazione e quindi si muove di moto
rettilineo uniforme.
Energia potenziale centrifuga
L’energia di un punto materiale P di massa m che si muove con velocità scalare v in un campo
1
di forze centrali e si trova a distanza r dal centro delle forze: E = E p ( r ) + m v 2
2
Poiché siamo in un campo di forze centrali, il moto è piano (il momento angolare si conserva,
ed in particolare la sua direzione resta costante); scriviamo allora la velocità vettoriale di P in
!
dr
d!
uˆ r + r
uˆ!
un sistema di coordinate polari nel piano del moto: v =
dt
dt
2
2
! !
& dr #
2
2
2
2 & d( #
e dunque il quadrato della velocità scalare vale v = v ' v = v r + v( = $ ! + r $
!
% dt "
% dt "
Sostituendo questa espressione in quella dell’energia otteniamo:
2
2
1 ! dr $ 1
2 ! d' $
E = E p (r ) + m # & + m r # &
" dt %
2 " dt % 2
Consideriamo, ancora, il momento angolare del punto materiale rispetto al centro delle forze:
!
! !
!
!
d!
L = m r " v = m (r " v r uˆ r + r " v! uˆ! ) = m r v! uˆ r " uˆ! = m r 2
uˆ z
dt
e quindi l’ultimo termine nell’espressione dell’energia può essere scritto in termini di modulo
del momento angolare, e prende il nome di energia potenziale centrifuga del punto materiale
2
1
L2
' d( $
P nel campo di forze centrali: m r 2 %
! E p(centr)
" =
2
2
2m r
& dt #
Poiché infatti questo termine non dipende esplicitamente dal modulo della velocità scalare,
ma solo dalla distanza r, come l’energia potenziale, può essere interpretato come se fosse
un’energia potenziale, benché in realtà sia stato ricavato dall’espressione dell’energia cinetica.
1
FISICA a.a. 2009-2010
Prof. G. Della Valle
Il suo effetto è lo stesso che avrebbe una forza repulsiva (centrifuga, appunto) apparente (in
un sistema non inerziale). Se infatti scegliamo un sistema di riferimento con l’asse z parallelo
all’asse di rotazione di P e che ruota con la stessa velocità angolare (istantanea) di P, in tale
sistema di riferimento abbiamo effettivamente una forza apparente centrifuga, e la sua
energia potenziale ha proprio l’espressione introdotta sopra, e il moto di P, in questo sistema
di riferimento, diventa monodimensionale, diretto lungo l’asse r. Per dimostrare l’asserto,
calcoliamo l’energia potenziale della forza centrifuga:
#
!
L2
L2
L2
ˆ
Fcentr = m% 2 r uˆ r =
u
!
L
=
dr
=
= E p(centr) (r )
r $#
3 r
3
2
"
mr
2m r
r mr
Energia potenziale efficace
Di conseguenza definiamo un’energia potenziale efficace del campo di forze centrale come la
somma dell’energia potenziale della forza del campo e dell’energia potenziale centrifuga:
L2
E p(eff ) ! E p + E p(centr) = E p ( r ) +
2m r 2
L’energia potenziale efficace rappresenta l’energia potenziale totale del punto materiale nel
sistema non inerziale sopra definito.
In un campo di forze centrali attrattivo, l’energia potenziale del campo è sempre negativa,
(come per il campo gravitazionale); l’energia potenziale efficace, invece, può essere negativa,
positiva o nulla a seconda che predomini il termine dovuto alla forza del campo o il termine
centrifugo (che è sempre positivo), o infine i due termini si bilancino esattamente.
Le condizioni iniziali del moto stabiliscono il valore del momento angolare, quindi
l’andamento dell’energia potenziale efficace al variare della distanza r, e l’energia totale del
punto materiale P, che si conserva durante il moto;
Il tipo di traiettoria che si ottiene dipende da queste due condizioni.
2
FISICA a.a. 2009-2010
Prof. G. Della Valle
2. Caratteristiche del moto in un campo di tipo gravitazionale
Consideriamo ora il caso di un campo di forze centrali attrattivo la cui energia potenziale
dipenda dall’inverso della distanza dal centro di forze, come nel caso del campo
gravitazionale percepito da una massa m in presenza di una massa M >> m, o come nel caso
del campo elettrostatico percepito da una particella carica leggera in presenza di una seconda
k
particella di carica opposta molto più pesante: E p ( r ) = ! .
r
L’energia potenziale efficace sarà dunque
E (eff)
k
L2
p (r )
(eff )
E p (r ) = ! +
r 2m r 2
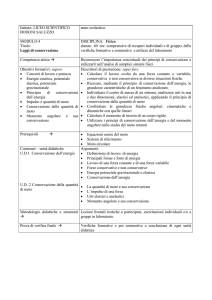
Osserviamo che l’energia potenziale efficace sarà
positiva per valori bassi di r, poiché in questo caso
E p(centr) (r )
E2
predomina il contributo centrifugo, inversamente
r0
proporzionale al quadrato di r, e negativa per valori
alti di r, dove predomina il contributo attrattivo,
raf
rmin
r
O
rz
inversamente proporzionale ad r (per r " ! tenderà
a zero, poiché entrambi i contributi tendono ad
E1
annullarsi) (vedi figura).
( eff )
Il valore limite che separa la zona a valori positivi da E p ,min r
per
L2
E p (r )
quella a valori negativi è: rz =
. Nella zona a
2km
valori negativi è presente il punto di minima energia
potenziale efficace, in corrispondenza della distanza
L2
doppia di quella per cui l’energia si annulla: rmin =
= 2rz . Il minimo di energia
km
k2m
(eff )
potenziale efficace vale: E p,min
= ! 2 .
2L
Caratteristiche del moto in un campo attrattivo di tipo gravitazionale
Applichiamo quando ricavato in precedenza per individuare le principali caratteristiche del
!
moto. Le condizioni iniziali stabiliscono il momento angolare L e l’energia totale E, che si
!
conservano; la direzione di L stabilisce il piano del moto, mentre dal suo modulo dipende
l’entità dell’energia potenziale centrifuga, e quindi i valori rz , rmin ed E p( eff,min) . Possiamo fare le
seguenti osservazioni:
2
1 ! dr $
Oss.1 Poiché risulta E = m # & + E p(eff ) ( r ) ' E p(eff ) ( r ) , avremo anzitutto che, fissato il
2 " dt %
2
1 ! dr $
valore di L, sarà certamente E ! E
, essendo sempre m # & una quantità positiva.
2 " dt %
L’uguaglianza, poi, può valere solo nel caso in cui la velocità radiale sia nulla (in modo che
l’energia totale coincida con l’energia potenziale efficace), ed al tempo stesso la distanza dal
centro delle forze corrisponda proprio al minimo di energia potenziale efficace. Inoltre:
( eff )
p , min
Oss.2 Se l’energia totale è negativa (E = E1 < 0 ), avremo che anche l’energia potenziale
efficace deve sempre restare negativa, ed in particolare al di sotto del valore E1 < 0 . Di
conseguenza il punto materiale P si trova confinato entro una buca di potenziale, e la sua
3
FISICA a.a. 2009-2010
Prof. G. Della Valle
distanza dal centro delle forze varierà tra un valore minimo ed un valore massimo (vedi
figura); la traiettoria, pertanto è una curva chiusa, che si dimostra essere una ellisse.
Il perielio e l’afelio si trovano alle distanze rper,af tali che sia:
k
L2
2
! 2kmrper,af + L2 = 0 =>
E p(eff ) ( rper,af ) = !
+
= ! E1 => E1 2m rper,af
2
rper,af 2m rper,af
2
=> rper
" k %
k
L2
=
! $
!
'
2 E1
# 2E1 & 2m E1
(eff )
con: E p,min
= !
2
" k %
k
L2
; raf =
+ $
!
'
2 E1
# 2E1 & 2m E1
k2m
" E1 < 0
2L2
Se, in particolare, l’energia totale (negativa) coincide con l’energia potenziale efficace
minima, la traiettoria è una circonferenza, ed infatti le distanze corrispondenti al perielio e
all’afelio vanno a coincidere perché la radice si annulla, ed entrambe valgono proprio rmin .
Oss.3 Se l’energia totale è positiva ( E = E2 > 0 ) , il punto materiale P è libero di sfuggire
alle forze del campo (vedi figura), la traiettoria è aperta, e si dimostra essere un’iperbole; il
massimo avvicinamento consentito al centro delle forze si determina imponendo velocità
radiale nulla e quindi uguaglianza fra l’energia potenziale efficace e l’energia totale. Si ottiene
il valore:
2
r0 =
! k $
L2
k
'
#
& +
" 2E2 % 2mE2 2E2
con
E2 > 0
(l’altra soluzione dell’equazione va scartata perché risulta negativa)
Oss.4 Se infine l’energia totale della particella è nulla, avremo che essa possiede l’energia
minima necessaria per sfuggire al campo, e la sua traiettoria si dimostra essere una parabola.
Il punto di massimo avvicinamento è a distanza rz , ove l’energia potenziale efficace si
annulla, e quindi coincide con l’energia totale.
Velocità di fuga
La velocità minima che un corpo deve possedere sul suolo di un pianeta per poter sfuggire al
campo gravitazionale del pianeta prende il nome di velocità di fuga.
Per calcolarla, in base a quanto visto sulla forma delle orbite, basta imporre che l’energia
totale del corpo sia nulla.
Infatti, all’istante iniziale (corpo sulla superficie del pianeta), avremo:
M m
M m 1
1
E p ,i = ! # T
; E c ,i = m vi2 " Ei = ! # T + m vi2
RT
2
RT
2
All’istante finale (corpo all’infinito), avremo invece:
E p, f = 0 ; Ec, f = 0 ! E f = 0
Poichè il sistema di forze è conservativo, dovrà essere ! "
equazione che fornisce la soluzione: vi = v fuga =
Terra.
4
MT m 1
+ m vi2 = Ei = E f = 0 ,
RT
2
2! M T
circa uguale ad 11.2 km/s per la
RT
FISICA a.a. 2009-2010
Prof. G. Della Valle
Oss. La velocità di fuga rappresenta la minima velocità iniziale che il punto materiale deve
avere al suolo per poter sfuggire all’attrazione gravitazionale del pianeta.
Oss. La velocità di fuga è la stessa in tutte le direzioni, essendo stata ricavata da un’equazione
scalare.
Oss. Notiamo infine che, per come è stata ricavata, la velocità di fuga è misurata rispetto ad
un sistema di riferimento assoluto, fermo rispetto al pianeta, che invece è in rotazione su se
stesso. Quindi la velocità di lancio rispetto alla superficie (SdR relativo) necessaria per la fuga
è inferiore alla velocità di fuga sopra calcolata, perchè un corpo fermo sulla superficie del
pianeta possiede già una velocità ben maggiore di zero nel SdR assoluto (fermo rispetto al
pianeta), pari alla velocità di trascinamento del SdR relativo, che ha modulo ! RT cos(" ) ,
direzione tangente al parallelo locale di latitudine ! e verso da ovest ad est. Poichè tale
velocità di trascinamento è massima all’equatore ( ! = 0), pari a circa 0.465 km/s per la Terra,
è più conveniente effettuare lanci spaziali da regioni equatoriali in direzione est (chiaramente
lanciare in direzione ovest non conviene se si vuole raggiungere la velocità di fuga!).
5