8 Sollecitazioni semplici
8.3 Flessione semplice retta
1
8.3.2 Equilibrio tra forze esterne e tensioni interne
Dimostrazione
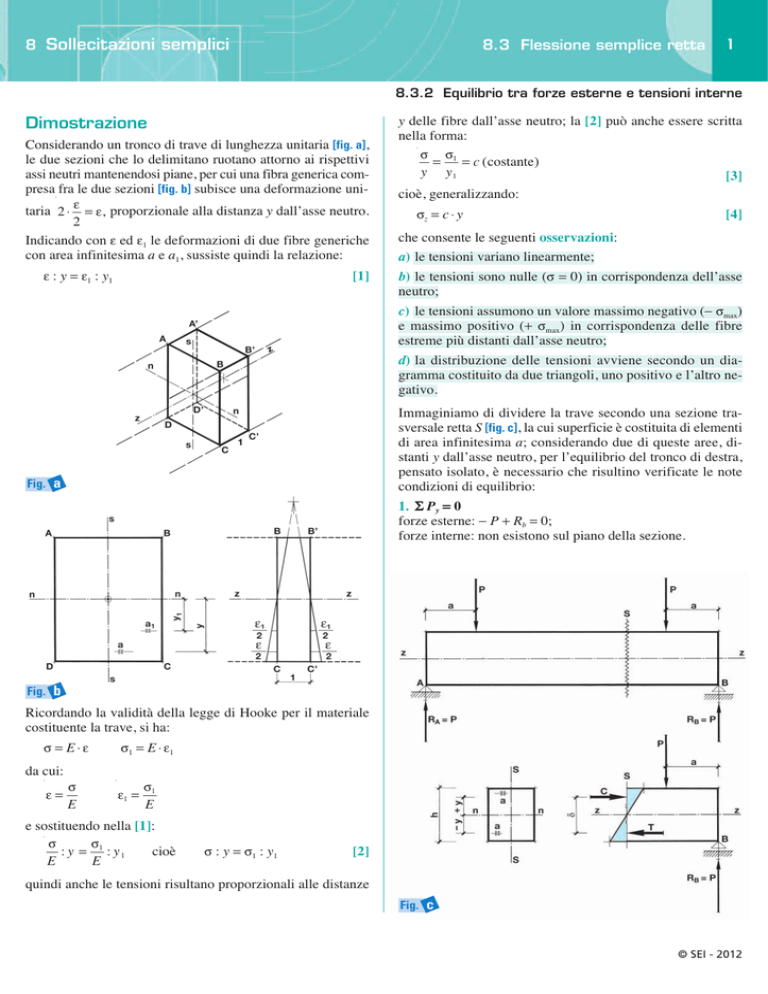
Considerando un tronco di trave di lunghezza unitaria [fig. a],
le due sezioni che lo delimitano ruotano attorno ai rispettivi
assi neutri mantenendosi piane, per cui una fibra generica compresa fra le due sezioni [fig. b] subisce una deformazione unitaria 2 ⋅
ε
= ε, proporzionale alla distanza y dall’asse neutro.
2
Indicando con ε ed ε1 le deformazioni di due fibre generiche
con area infinitesima a e a1, sussiste quindi la relazione:
ε : y = ε1 : y1
[1]
y delle fibre dall’asse neutro; la [2] può anche essere scritta
nella forma:
σ
y
=
σ1
y1
= c (costante)
[3]
cioè, generalizzando:
σz = c ⋅ y
[4]
che consente le seguenti osservazioni:
a) le tensioni variano linearmente;
b) le tensioni sono nulle (σ = 0) in corrispondenza dell’asse
neutro;
c) le tensioni assumono un valore massimo negativo (− σmax)
e massimo positivo (+ σmax) in corrispondenza delle fibre
estreme più distanti dall’asse neutro;
d) la distribuzione delle tensioni avviene secondo un diagramma costituito da due triangoli, uno positivo e l’altro negativo.
Immaginiamo di dividere la trave secondo una sezione trasversale retta S [fig. c], la cui superficie è costituita di elementi
di area infinitesima a; considerando due di queste aree, distanti y dall’asse neutro, per l’equilibrio del tronco di destra,
pensato isolato, è necessario che risultino verificate le note
condizioni di equilibrio:
Fig. a
1. S Py = 0
forze esterne: − P + Rb = 0;
forze interne: non esistono sul piano della sezione.
Fig. b
Ricordando la validità della legge di Hooke per il materiale
costituente la trave, si ha:
σ = E⋅ε
σ1 = E ⋅ ε1
da cui:
ε=
σ
ε1 =
E
σ1
E
e sostituendo nella [1]:
σ
E
:y =
σ1
E
: y1
cioè
σ : y = σ1 : y1
[2]
quindi anche le tensioni risultano proporzionali alle distanze
Fig. c
© SEI - 2012
8 Sollecitazioni semplici
8.3 Flessione semplice retta
2
8.3.2 Equilibrio tra forze esterne e tensioni interne
2. S Px = 0
forze esterne: non esistono;
forze interne: sono rappresentate dalle tensioni normali σz ⋅ a
di compressione e di trazione, le cui risultanti sono rispettivamente C e T; per l’equilibrio della sezione deve essere:
all’asse neutro, tenendo conto che il centro dei momenti di
una coppia può essere qualunque punto del piano, cioè:
0
h
M i = ∑ ( σ z ⋅ a⋅ y) = M
0
e sostituendo a σz il valore fornito dalla [4] e tenendo presente
la [3] si ottiene:
0
h
∑ ( σ z ⋅ a) = 0
[5]
0
oppure C + T = 0, cioè C = − T, e quindi le due risultanti sono
uguali in valore assoluto e verso contrario.
Sostituendo nella [5] il valore di σz dato dalla [4] si ha:
h
∑ (c ⋅ y ⋅ a) = 0
0
h
ossia
c ⋅ ∑ (a⋅ y) = 0
0
h
ma ∑ (a⋅ y) rappresenta il momento statico della sezione ri0
spetto all’asse neutro, che è quindi baricentrico, essendo il
momento nullo.
3. S M = 0
momento esterno: M = P ⋅ a;
momento interno: è rappresentato dal momento della coppia
formata dalle forze interne C e T, cioè:
Mi = T ⋅ δ
(oppure Mi = C ⋅ δ)
h
h
σ h
M = ∑ (c ⋅ y ⋅ a⋅ y) = c ⋅ ∑(a ⋅ y2) = ⋅ ∑(a ⋅ y2)
0
0
y 0
h
ma il termine ∑ (a⋅ y 2 ) rappresenta il momento d’inerzia I
0
della sezione rispetto all’asse neutro baricentrico, per cui:
M=
σ
y
⋅I
da cui:
σ=m
M ⋅y
(N/mm2)
I
[6]
detta formula di Navier, che fornisce la tensione σ in un
punto generico della sezione distante m y dall’asse neutro e
che rappresenta la formula generale della flessione semplice.
Per l’equilibrio deve risultare M = Mi; quest’ultimo può essere espresso anche in funzione delle tensioni normali rispetto
© SEI - 2012