SCHEDA 5.2
La curva normale
La curva normale (detta anche curva di Laplace-Gauss) è un tipo di
distribuzione delle frequenze relative (o, più precisamente, di densità di
frequenze relative) condiviso da numerose famiglie di dati, soprattutto
antropometrici, come statura, peso o quoziente intellettuale.
0.7
0.6
0.5
0.4
68.27%
0.3
0.2
0.1
0
µ-2σ
µ-σ
µ
µ+σ
µ+2σ
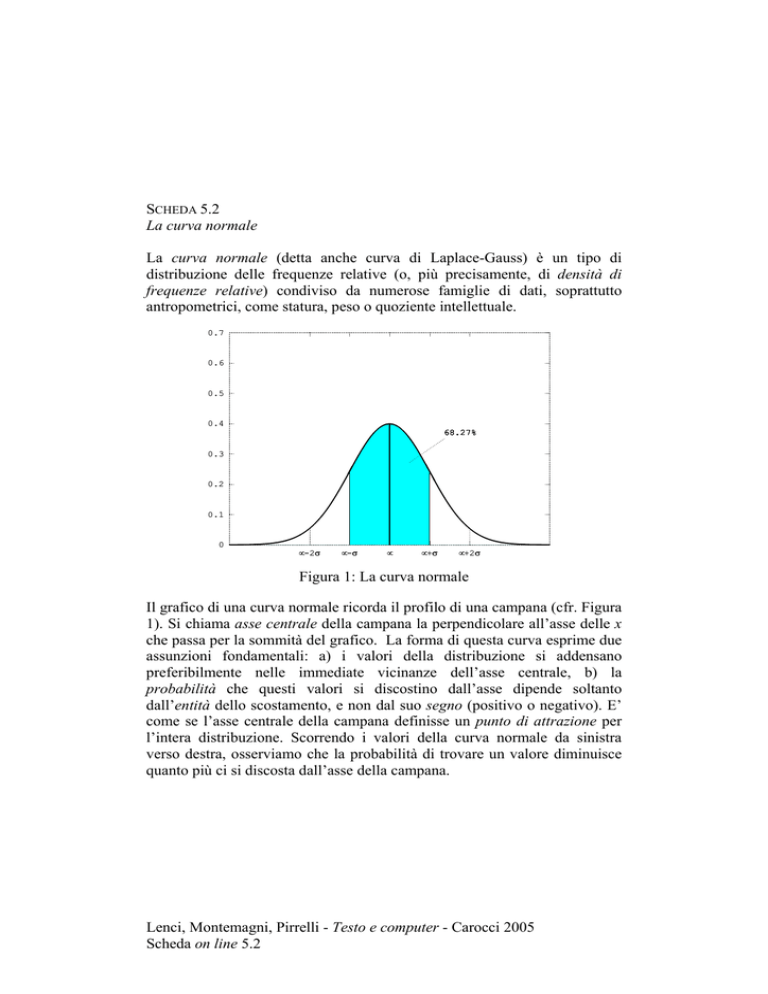
Figura 1: La curva normale
Il grafico di una curva normale ricorda il profilo di una campana (cfr. Figura
1). Si chiama asse centrale della campana la perpendicolare all’asse delle x
che passa per la sommità del grafico. La forma di questa curva esprime due
assunzioni fondamentali: a) i valori della distribuzione si addensano
preferibilmente nelle immediate vicinanze dell’asse centrale, b) la
probabilità che questi valori si discostino dall’asse dipende soltanto
dall’entità dello scostamento, e non dal suo segno (positivo o negativo). E’
come se l’asse centrale della campana definisse un punto di attrazione per
l’intera distribuzione. Scorrendo i valori della curva normale da sinistra
verso destra, osserviamo che la probabilità di trovare un valore diminuisce
quanto più ci si discosta dall’asse della campana.
Lenci, Montemagni, Pirrelli - Testo e computer - Carocci 2005
Scheda on line 5.2
Una curva normale è completamente definita dalla sua media µ e
deviazione standard σ. In particolare, µ coincide con il valore dell’ascissa su
cui cade l’asse centrale. Da σ dipende invece la curtosi della campana, cioè
il suo grado di appiattimento. Al crescere di σ, infatti, diminuisce l’altezza
della campana ed aumenta allo stesso tempo la sua ampiezza.
Esiste una relazione importante tra una distribuzione di questo tipo e
la nozione di probabilità. In generale, se si tracciano due verticali all’asse
delle x che passano per i punti x' e x'+δ, si avrà che l’area della “fetta”
compresa tra le due verticali, l’asse delle x e la curva normale, corrisponde
alla probabilità di trovare un valore compreso tra x' e x'+δ. In particolare,
nella curva normale l’area della “fetta” di campana compresa tra i punti
µ + σ e µ − σ è uguale al 68,27% dell’area totale sottesa alla curva (v.
Figura S3). Questo vuol dire che se i nostri dati sono distribuiti
normalmente, allora il 68,27% degli stessi si discosta da µ di un valore non
superiore alla deviazione standard della loro distribuzione. Allargando
ancora la nostra fetta centrata sull’asse, osserviamo che il 95% dei dati è
compreso tra µ − 1,96·σ e µ + 1,96·σ, e che più del 99% non si discosta da µ
(in positivo o in negativo) di più di 3 volte σ.
Lenci, Montemagni, Pirrelli - Testo e computer - Carocci 2005
Scheda on line 5.2











