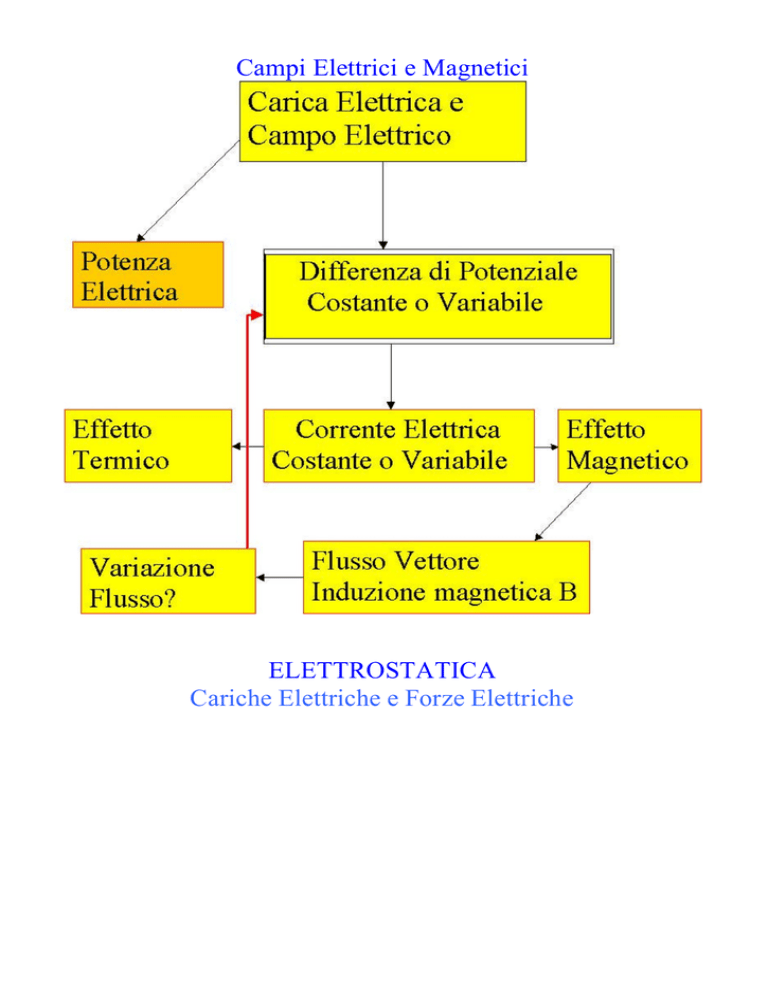
Campi Elettrici e Magnetici
ELETTROSTATICA
Cariche Elettriche e Forze Elettriche
Esperienza ==> Forza tra cariche
SI INTRODUCE UNA NUOVA GRANDEZZA FONDAMENTALE: LA
CARICA ELETTRICA
UNITÀ DI MISURA NEL S.I.: COULOMB
SI OSSERVA SPERIMENTALMENTE CHE, DATE DUE CARICHE Q 1 E Q 2
POSTE A DISTANZA r, QUESTE SI RESPINGONO (SE SONO DELLO
STESSO SEGNO) OPPURE SI ATTRAGGONO (SE SONO DI SEGNO
OPPOSTO) CON UNA FORZA DIRETTA LUNGO LA CONGIUNGENTE
DELLE CARICHE E DIPENDENTE DALL ’INVERSO DELLA DISTANZA:
LA COSTANTE ε0 E’ DETTA PERMITTIVITA ’ DEL VUOTO E VALE:
ε0 = 8.854 ⋅ 10 -12 (C 2/N⋅ m2)
DALL’OSSERVAZIONE SPERIMENTALE DELLA FORZA CHE SI
ESERCITA TRA DUE CARICHE, PUò ESSERE DEFINITA L ’UNITA ’
DICARICA ELETTRICA, IL COULOMB: DATI DUE CORPI AVENTI LA STESSA
CARICA ELETTRICA SI DEFINISCE COULOMB (C) LA CARICA
ELETTRICA POSSEDUTA DA CIASCUNO DEI DUE SE, POSTI ALLA
DISTANZA DI 1 m, SI RESPINGONO CON LA FORZA DI:
F = 8.99⋅ 10 9 N
CAMPO ELETTRICO
SIA q UNA PICCOLA "CARICA DI PROVA"; SI OSSERVA
SPERIMENTALMENTE CHE LA FORZA CHE AGISCE SULLA CARICA SI
PUÒ SCRIVERE COME:
E E’ CHIAMATO CAMPO ELETTRICO.
OSSERVIAMO CHE IL CAMPO ELETTRICO E ’ UN VETTORE; QUESTO
SIGNIFICA CHE IL CAMPO ELETTRICO GENERATO DA DUE (O PIU ’)
CARICHE ELETTRICHE E’ IL VETTORE OTTENUTO COME SOMMA
VETTORIALE DEL CAMPO ELETTRICO DI CIASCUNA CARICA .
DALLA LEGGE DI COULOMB FACILMENTE VEDIAMO CHE IL CAMPO
ELETTRICO DI UNA CARICA PUNTIFORME Q È DATO DA:
LINEE DI FORZA DEL CAMPO ELETTRICO : UNA DESCRIZIONE
INTUITIVAMENTE COMPRENSIBILE DELLA DIPENDENZA SPAZIALE
DEL CAMPO ELETTRICO E ’ DATA DALLE LINEE DI FORZA:
UNA LINEA DI FORZA È TALE CHE IN OGNI PUNTO LA TANGENTE
ORIENTATA HA DIREZIONE E VERSO DEL CAMPO ELETTRICO E IN
QUEL PUNTO.
IN PARTICOLARE, AD ESEMPIO, LE LINEE DI FORZA DI UNA CARICA
PUNTIFORME SONO DIRETTE RADIALMENTE VERSO L’ESTERNO SE
LA CARICA È POSITIVA O VERSO IL CENTRO SE LA CARICA È
NEGATIVA.
POTENZIALE ELETTROSTATICO
IL CAMPO ELETTROSTATICO È CONSERVATIVO:
SAPPIAMO ALLORA CHE PU Ò ESSERE DEFINITA UNA FUNZIONE -IN
QUESTO CASO CHIAMATA POTENZIALE ELETTROSTATICO V - TALE
CHE:
LA QUANTITÀ V(A) - V(B) SI CHIAMA DIFFERENZA DI POTENZIALE
(ddp).
RICORDANDO CHE, DATA UNA CARICA DI PROVA q, IL CAMPO
ELETTRICO ESERCITA UNA FORZA:
LA DIFFERENZA DI POTENZIALE TRA DUE PUNTI DELLO SPAZIO
PUO’ ESSERE ESPRESSA COME IL RAPPORTO TRA IL LAVORO FATTO
DAL CAMPO SU UNA CARICA DI PROVA q E LA CARICA q STESSA:
LA DIFFERENZA DI POTENZIALE SI MISURA IN VOLT:
1 V = 1 JOULE / 1 COULOMB
OSSERVIAMO INFINE CHE PER LE DIMENSIONI DEL CAMPO
ELETTRICO ABBIAMO:
[E] [L] = [V] ⇒ [E] = [V]/[L]
PERTANTO IL CAMPO ELETTRICO SI MISURA IN Volt/m.
CORRENTE ELETTRICA E LEGGE DI OHM
L’INTENSITÀ DI CORRENTE ELETTRICA ATTRAVERSO UNA DATA
SUPERFICIE È LA QUANTITÀ DI CARICA CHE ATTRAVERSA LA
SUPERFICIE NELL’UNITÀ DI TEMPO:
i = dQ/dt
AD ESEMPIO L’INTENSITÀ DI CORRENTE CHE PERCORRE UN FILO
CONDUTTORE È LA QUANTITÀ DI CARICA CHE NELL’UNITÀ DI
TEMPO ATTRAVERSA LA SEZIONE DEL FILO.
NEL SISTEMA S.I. LA CORRENTE SI MISURA IN AMPERE:
1A=1C/1s
LEGGE DI OHM: SPERIMENTALMENTE OHM OSSERVO ’ CHE
L’INTENSITÀ DI CORRENTE ELETTRICA CHE PERCORRE UN FILO
CONDUTTORE È PROPORZIONALE ALLA DIFFERENZA DI
POTENZIALE TRA GLI ESTREMI:
∆V = i R
LA COSTANTE DI PROPORZIONALITA ’, R, E’ OGGI CHIAMATA
RESISTENZA E SI MISURA IN OHM, NEL SISTEMA INTERNAZIONALE:
UN CONDUTTORE HA RESISTENZA UGUALE A 1 Ω (OHM) SE È
PERCORSO DA 1 A DI CORRENTE QUANDO LA ddp AI SUOI CAPI È 1 V.
IL VALORE DELLA RESISTENZA DIPENDE, OLTRE CHE DAL TIPO DI
MATERIALE, DALLA’AREA DELLA SEZIONE E DALLA
TEMPERATURA.
SPERIMENTALMENTE SI OSSERVA CHE LA RESISTENZA DI UN FILO
OMOGENEO DI SEZIONE COSTANTE RISULTA PROPORZIONALE
ALLA LUNGHEZZA L DEL FILO ED INVERSAMENTE PROPORZIONALE
ALLA SEZIONE S:
R = ρc⋅L/S
IL COEFFICIENTE ρc, CHE DIPENDE DAL MATERIALE E DALLA TEMPERATURA, SI
CHIAMA RESISTIVITÀ.
VALORI DELLA RESISTIVITÀ PER VARIE SOSTANZE, A
TEMPERATURA T = 20 °C, SONO RIPORTATE IN TABELLA.
ρc (Ω m)
SOSTANZA
Argento
0.167 10 -7
Rame
0.172 10 -7
Metalli: Alluminio
0.283 10 -7
Tungsteno
Mercurio
0.551 10 -7
9.6 10-7
4.42 10-7
Costantana
(Cu 60%, Ni 40%)
4.35 10-7
Leghe:
Manganina
(Cu 80%, Mn 14%, Ni 4%)
Germanio
0.45
Silicio
640
Vetro
≈ 10 12
Ceralacca
≈ 10 14
Semiconduttori:
Isolanti:
Zolfo
Quarzo
≈ 10 15
7.5 1017
RESISTENZE IN SERIE ED IN PARALLELO
PIU’ CONDUTTORI POSSONO VENIRE COLLEGATI TRA DI LORO IN
VARI MODI PER OTTENERE CIRCUITI DI FORME DIVERSE, CHE
POSSONO ESSERE RICONDOTTE ALLE CONNESSIONI
FONDAMENTALI DI SERIE E PARALLELO:
1.
DUE CONDUTTORI SI DICONO IN SERIE SE SONO ATTRAVERSATI
DALLA STESSA CORRENTE i.
2.
DUE CONDUTTORI SI DICONO IN PARALLELO SE AI LORO CAPI VI
E’ LA STESSA DIFFERENZA DI POTENZIALE.
CONSIDERIAMO LE RESISTENZE DI FIGURA 1: ESSE SONO
ATTRAVERSATE DALLA STESSA CORRENTE, DUNQUE SONO IN
SERIE.
DALLA LEGGE DI OHM APPLICATA A CIASCUNA RESISTENZA
ABBIAMO:
SOMMANDO MEMBRO A
MEMBRO OTTENIAMO:
POICHE’ (V1 – V3) E’ LA DIFFERENZA AI CAPI DEL CIRCUITO
RISULTANTE, LE DUE RESISTENZE IN SERIE EQUIVALGONO AD UN
UNICA RESISTENZA DEL VALORE UGUALE ALLA SOMMA DELLE
DUE.
GENERALIZZANDO POSSIAMO SCRIVERE CHE LA RESISTENZA
COMPLESSIVA DI PIU’ CONDUTTORI DISPOSTI IN SERIE E ’ LA
SOMMA DELLE RESISTENZE DEI SINGOLI CONDUTTORI.
NEL CASO DI RESISTENZE IN PARALLELO, COME INDICATO IN
FIGURA SEGUENTE, SE ∆ V INDICA LA ddp AI CAPI DEL CIRCUITO,
POSSIAMO SCRIVERE:
SOMMANDO VEDIAMO CHE LA CORRENTE COMPLESSIVA i = i 1 + i2 E’
UGUALE A:
CHE POSSIAMO GENERALIZZARE NELLA LEGGE: IL RECIPROCO
DELLA RESISTENZA COMPLESSIVA DI DUE O PIU’ RESISTENZE
POSTE IN PARALLELO E’ UGUALE ALLA SOMMA DEI RECIPROCI
DELLE RESISTENZE.
EFFETTO JOULE
CONSIDERIAMO UN CONDUTTORE AVENTE DIFFERENZA DI
POTENZIALE ∆V AI SUOI ESTREMI E PERCORSO DALLA CORRENTE i.
RICORDANDO LA DEFINIZIONE DI POTENZIALE ELETTROSTATICO,
OSSERVIAMO CHE NEL TEMPO dt, IL CAMPO ELETTRICO COMPIE
LAVORO POSITIVO:
IN UN CONDUTTORE IL LAVORO FATTO DAL CAMPO ELETTRICO
NON SI TRADUCE IN UNA VARIAZIONE DI ENERGIA CINETICA DELLE
CARICHE SU CUI SI ESERCITA LA FORZA. LA VELOCITA ’ MEDIA DI
CIASCUNA CARICA DENTRO IL CONDUTTORE RESTA INFATTI
COSTANTE DURANTE IL PERCORSO.
COME OSSERVO’ SPERIMENTALMENTE JOULE, IL LAVORO
COMPIUTO DAL CAMPO VIENE TRASFORMATO IN CALORE . LA
POTENZA DISSIPATA IN CALORE PER EFFETTO JOULE PUO ’ ESSERE
CALCOLATA UTILIZZANDO LA FORMULA PRECEDENTE E LA LEGGE
DI OHM:
LE APPLICAZIONI PRATICHE BASATE SULL’EFFETO JOULE SONO
MOLTISSIME: I FILAMENTI DELLE LAMPADINE SI SCALDANO ED
ILLUMINANO, LE STUFE ELETTRICHE RISCALDANO, I FERRI DA
STIRO...E COSI’ VIA.












