Elaborato individuale di Elettrotecnica Industriale a/a 2012/2013
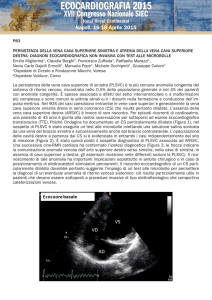
ES. 1 – Polo magnetico
A
t
B
Materiale ferromagnetico con permeabilità μ=μ0μr
Avvolgimento, porta una densità di corrente J
Mezzo dielettrico
L’obiettivo è studiare l’andamento del campo magnetico, prodotto
dall’avvolgimento, nel sistema in esame con particolare attenzione a quello
che succede nel traferro t.
Si analizzi, sia nel caso di materiale lineare che non lineare, come si
modifica il campo al variare della geometria del problema: spessore del
traferro, dimensione della cava e dimensione dell’avvolgimento.
Si analizzi inoltre la condizione di transitorio: si supponga di imprimere,
per t=0, un gradino di corrente nell’avvolgimento. Studiare quindi la
diffusione del campo magnetico nel sistema, dall’istante iniziale fino alla
condizione di regime.
ES. 2a →Cava chiusa
+b
-a
I
+a
-b
Cava di dimensioni (2a,2b)
Materiale ferromagnetico
Corrente di conduzione concentrata (primo caso)
Corrente di conduzione concentrata (secondo caso)
Questo problema considera una cava rettangolare in un mezzo di materiale
ferromagnetico (la cui permeabilità è quindi molto maggiore di quella
della cava).
Si suppone che una corrente I sia localizzata nel centro di gravità della
cava (primo caso).
Si vuole studiare l’andamento del campo generato da I nella cava al variare
delle dimensioni della cava.
Si supponga, successivamente, che la corrente non sia distribuita in cava
ma concentrata in due conduttori filiformi disposti simmetricamente lungo
l’asse maggiore (secondo caso). Risolvere il problema anche in questo
caso usando il metodo delle immagini.
ES. 2b →Cava aperta
+b
-a
I
+a
-b
Cava di dimensioni (2a,2b)
Materiale ferromagnetico
Corrente di conduzione localizzata
Corrente di conduzione concentrata (secondo caso)
Questo problema considera una cava rettangolare in un mezzo di materiale
ferromagnetico (la cui permeabilità è quindi molto maggiore di quella della cava). A
differenza del caso precedente, un lato della cava non è a contatto con il materiale
ferromagnetico ma è affacciato al traferro
Cambiano di conseguenza le condizioni al contorno.
Si suppone che una corrente I sia localizzata nel centro di gravità della cava (primo
caso).
Si vuole studiare l’andamento del campo generato da I nella cava al variare delle sue
dimensioni.
Si supponga che la corrente non sia distribuita in cava ma concentrata in due
conduttori filiformi disposti simmetricamente lungo l’asse maggiore (secondo caso).
Risolvere il problema anche in questo caso usando il metodo delle immagini.
Si supponga che la corrente sia uniformemente distribuita nella cava. Risolvere il
problema usando il metodo della separazione delle variabili.
ES. 2c → Cava in un mezzo diamagnetico
+b
-a
I
+a
-b
Cava di dimensioni (2a,2b) di permeabilità μr
Materiale diamagnetico
Corrente di conduzione distribuita
La cava, immersa in un mezzo diamagnetico (μr<<1), ospita un conduttore
esteso di sezione (2a,2b).
Studiare l’andamento del campo magnetico nella cava.
Per la risoluzione analitica si usi il metodo di separazione delle variabili e
lo sviluppo in serie di Fourier della funzione potenziale vettore.
ES. 3 →Azioni meccaniche fra due conduttori
y2
y1
I1
I2
D
a
Conduttore di sezione a×b
Mezzo illimitato con permeabilità relativa μr
Correnti di conduzione
Due sbarre conduttrici di uguale sezione, percorse da correnti I1 e I2, sono immerse in
un mezzo avente permeabilità μr.
Si vuole calcolare la forza risultante lungo l’asse x dall’interazione magnetica fra i
due conduttori al variare delle loro dimensioni e della distanza D.
Si risolva numericamente il problema usando il metodo degli elementi finiti
Si calcoli anche la forza agente lungo l’asse nel caso in cui y1≠y2.
ES 3a→ Per il calcolo delle azioni meccaniche si usi il metodo dei lavori virtuali;
ES 3b→ Per la risoluzione analitica del problema di campo magnetico usare il
metodo della funzione di Green;
ES 3c→ Per il calcolo delle azioni meccaniche si usi il metodo del tensore degli
sforzi di Maxwell;
ES 3d→ Per il calcolo delle azioni meccaniche si usi il principio di Lorentz.
ES. 4 → Azioni meccaniche su un superconduttore
SUPERCONDUTTORE
MAGNETI PERMANENTI
FERRO
I superconduttori HTSC (high temperature superconductors) possono
essere sfruttati per produrre dei “cuscinetti senza attrito” nelle macchine
rotanti. Fra i magneti e il superconduttore si genera una forza repulsiva il
cui effetto è la “levitazione” dell’albero rotante, con il conseguente
annullamento degli attriti.
Lo scopo dell’esercitazione è di studiare la geometria dei magneti
(assegnata quella del superconduttore) in modo tale da aumentare la forza
di levitazione, mantenendo il volume dei magneti permanenti entro limiti
accettabili. Si modelli il superconduttore come mezzo diamagnetico
(μr<<1). Sarà necessario anche valutare come modellizzare il problema
per la risoluzione a elementi finiti (parametri delle regioni, tipo di griglia).
Per il calcolo delle azioni meccaniche si può utilizzare uno dei metodi
proposti nell’esercizio 3: lavori virtuali, tensore degli sforzi di Maxwell,
principio di Lorentz.
ES. 5 → Motore a magneti permanenti
La figura rappresenta la sezione trasversale di un motore sincrono a
magneti permanenti.
Si assumano i seguenti dati geometrici:
R_shaft= 10 mm
R_rotor= 30 mm
R_int_stator= 30.5 mm
R_ext stator= 50 mm
D_ventilating_slot= 4 mm
AirGap width d= 0.5 mm
Magnet to airgap distance tm= 1.7 mm
Slot opening bs= 2.9 mm
Si studi la coppia di impuntamento al variare della posizione angolare relativa α fra
statore e rotore (avvolgimento trifase a vuoto).
Per il calcolo della coppia si applichi il metodo dei lavori virtuali o del tensore degli
sforzi di Maxwell.
Facendo opportune ipotesi sul numero di spire per cava e sulle dimensioni della cava,
valutare la forza elettromotrice che si sviluppa (vedere gli appunti della lezione del
prof. Palka), valutando la curva “fem vs posizione” angolare.
ES. 6 → Calcolo delle induttanze
Ω1
I1
Ω’1
I2
Ω2
I1
Ω’2
I2
aria
Conduttore percorso da una corrente I1, diviso in due regioni
Ω1 e Ω2
Conduttore percorso da una corrente I2, diviso in due regioni
Ω’1 e Ω’2
Si vogliono ricavare le autoinduttanze (L11 e L22) e la mutua induttanza
(M12) equivalenti del sistema in modo tale da poterne fornire una
rappresentazione circuitale. Si supponga che il mezzo magnetico sia
lineare.
Si studi come si modificano questi parametri al variare della posizione
reciproca fra la coppia Ω1 - Ω2 e la coppia Ω’1 - Ω’2 (traslazione e
rotazione).
ES. 7 → Problema accoppiato elettrotermico
σ
J0
ΩT
Ωm
Conduttore (1) sede di corrente impressa
Conduttore (2) sede di corrente indotta
Si consideri la geometria assial-simmetrica riportata in figura.
Per una descrizione più approfondita del problema si rimanda alla dispensa
sui “problemi accoppiati”.
Si studi il sistema secondo il modello elettrotermico.
Studiare l’andamento del campo magnetico in tutto il dominio e del campo
di temperatura nel sottodominio ΩT per una corrente specifica impressa J0
di frequenza assegnata. Sarà necessario modellizzare il sistema sia da un
punto di vista magnetico che termico.
Studiare il campo di reazione nella sottoregione ΩT (ed eventualmente
anche nell’avvolgimento) nel dominio della frequenza, valutando quindi
come varia l’effetto delle correnti parassite al variare della frequenza.