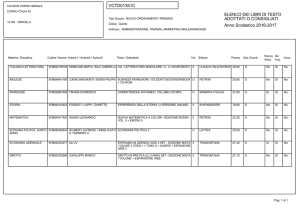
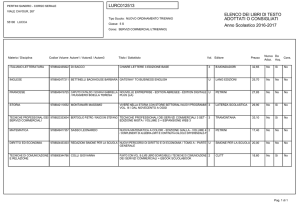
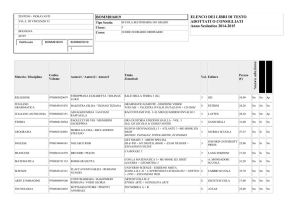
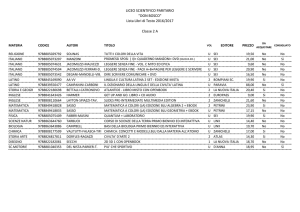
Anno scolastico 2013-2014
BIENNI:
“Amministrazione, finanze e marketing”
Articolazione Amministrazione, finanze e marketing
“Chimica, Materiali e Biotecnologie”
Articolazione Biotecnologie sanitarie
“Elettronica ed Elettrotecnica”
Articolazione Automazione
“Informatica e telecomunicazioni”
Articolazione Informatica
PROGRAMMA PREVENTIVO
MATEMATICA
Ore settimanali 4
DOCENTE
Severina Caroli
Roberta Frigerio
Francesca Donadio
Antonella Ravera
Cinzia Mandelli
Laura Pasini
Giuseppina Ferreri
Fulvia Avalle
Monica Terenghi
Giuseppina Pizzoni
Franco Tornaghi
Francesca Berengo
CLASSE
1A
2A
1B
2B
Amministrazione finanze e marketing
Amministrazione finanze e marketing
Amministrazione finanze e marketing
Amministrazione finanze e marketing
1A Chimica, materiali e biotecnologie
2A Chimica, materiali e biotecnologie
1B Chimica, materiali e biotecnologie
2B Chimica, materiali e biotecnologie
1C Chimica, materiali e biotecnologie
2C Chimica, materiali e biotecnologie
2D Chimica, materiali e biotecnologie
1A Elettronica ed elettrotecnica
2A Elettronica ed elettrotecnica
1B Elettronica ed elettrotecnica
1A informatica e telecomunicazioni
2A informatica e telecomunicazioni
1B informatica e telecomunicazioni
2B informatica e telecomunicazioni
1C informatica e telecomunicazioni
2C informatica e telecomunicazioni
FINALITA' E OBIETTIVI
COMPETENZE TRASVERSALI
Il docente di Matematica concorre a far conseguire allo studente, al termine del percorso
quinquennale, risultati di apprendimento che lo mettano in grado di:
padroneggiare il linguaggio formale e i procedimenti dimostrativi della matematica
possedere gli strumenti matematici, statistici e del calcolo delle probabilità necessari per la
comprensione delle discipline scientifiche e per poter operare nel campo delle scienze
applicate
collocare il pensiero matematico e scientifico nei grandi temi dello sviluppo della storia
delle idee, della cultura, delle scoperte scientifiche e delle invenzioni tecnologiche.
COMPETENZE DELLA DISCIPLINA
Ai fini del raggiungimento dei risultati di apprendimento sopra riportati in esito al percorso
quinquennale, nel primo biennio il docente persegue, nella propria azione didattica ed educativa,
l’obiettivo prioritario di far acquisire allo studente le competenze di base attese a conclusione
dell’obbligo di istruzione, di seguito richiamate:
utilizzare le tecniche e le procedure di calcolo aritmetico ed algebrico rappresentandole anche
sotto forma grafica
confrontare ed analizzare figure geometriche, individuando invarianti e relazioni
individuare le strategie appropriate per la soluzione di problemi
analizzare dati e interpretarli sviluppando deduzioni e ragionamenti sugli stessi anche con
l’ausilio di rappresentazioni grafiche, usando consapevolmente gli strumenti di calcolo e le
potenzialità offerte da applicazioni specifiche di tipo informatico
METODOLOGIA DIDATTICA
Gli argomenti del programma saranno affrontati secondo i seguenti criteri:
sarà privilegiato l’aspetto di costruzione personale e consapevole dei concetti, attraverso la
proposta di situazioni problematiche, modelli, esempi e controesempi
sarà favorito l’approccio alle varie tematiche da molteplici punti di vista, suggeriti
dall’insegnante o frutto dell’esperienza personale degli alunni
verranno sviluppati, ove possibile, attività e contenuti interdisciplinari per favorire
l’apprendimento e rafforzare la motivazione.
Il percorso didattico, comprese eventuali iniziative volte al recupero, si svilupperà attraverso:
attività in aula:
lezioni frontali
lezioni dialogate
lavoro di gruppo (per introdurre nuovi argomenti, consolidare capacità operative,
individuare strategie risolutive di problemi, ...)
esercitazioni
prove di verifica
attività in laboratorio di informatica e/o in aula col netbook: utilizzo di applicativi (es. word
processor, foglio elettronico, software di manipolazione simbolica, software di geometria
dinamica) e di risorse didattiche digitali per introdurre, esemplificare, studiare e approfondire i
contenuti disciplinari;
utilizzo di schede preparate dall’insegnante
utilizzo dei libri di testo
CRITERI DI VALUTAZIONE
La valutazione delle prove di verifica avverrà secondo la seguente corrispondenza:
Sigla sul
GIUDIZIO
VOTO
registro
PRESTAZIONE
NULLO-NEGATIVO
1
NULLO-NEGATIVO
2
NEGATIVO
3
GI
GRAV.
4
INSUFFICIENTE
I
5
SC
5,5
SUFFICIENTE
S
6
DISCRETO
D
7
BUONO
B
8
INSUFFICIENTE
SCARSO
OTTIMO
ECCELLENTE
9
O
10
DESCRITTORI
lo studente non ha conoscenze relative agli argomenti
trattati
ha conoscenze scarse e frammentarie e commette molti
errori
ha conoscenze lacunose e/o commette errori
nell’applicazione
ha conoscenze superficiali e/o commette errori
nell’applicazione
ha conoscenze non approfondite che applica senza
commettere numerosi o gravi errori
ha conoscenze che sa applicare adeguatamente
ha conoscenze approfondite che sa applicare
adeguatamente e ha capacità di analisi e sintesi
ha conoscenze approfondite, capacità di analisi e di
sintesi, è in grado di organizzare le sue conoscenze in
modo autonomo scegliendo opportunamente le
procedure adeguate alle situazioni
In particolare il livello della sufficienza si collocherà, di norma, al superamento di prove costituite da esercizi che
possano essere risolti seguendo uno schema ben preciso già applicato in classe, in situazioni simili a quelle proposte
nella verifiche; inoltre i calcoli e la comprensione/utilizzazione del linguaggio matematico non richiederanno particolari
abilità.
NB: segue la descrizione del percorso didattico previsto nel biennio; gli obiettivi specifici di
apprendimento sono declinati in termini di conoscenze e abilità. La suddivisione del percorso
nei due anni del biennio è indicativa, e ogni docente potrà scegliere, in funzione del proprio
stile didattico e degli stili di apprendimento dei propri alunni, ferme restando la coerenza
complessiva e le esigenze intrinseche della disciplina, di modificare il percorso, anticipando o
rimandando alcuni moduli o segmenti di essi.
CONTENUTI
CLASSI PRIME
Il linguaggio della matematica:
(trasversale rispetto agli altri temi e ai due anni del biennio)
Conoscenze
Costanti, parametri, variabili
Abilità
Distinguere in una frase soggetti e predicati, operazioni
e relazioni
Proposizioni e frasi aperte
Insieme di verità di una frase aperta
Distinguere espressioni e formule, proposizioni aperte
e proposizioni
I connettivi e, o, non e relativi valori di verità’
Distinguere ed utilizzare costanti, parametri, variabili
Operazioni tra insiemi: , , complementare e
relative proprieta’
Tradurre dal linguaggio naturale a quello grafico a
quello simbolico e viceversa
Distinguere termini primitivi e definizioni, assiomi e
teoremi
Distinguere tra verifica e dimostrazione
Distinguere tra esempio e controesempio
Riconoscere proposizioni semplici e composte
mediante le preposizioni e, o, non (*)
Riconoscere ed utilizzare condizioni necessarie,
sufficienti, necessarie e sufficienti.(*)
Riconoscere una frase aperta(*)
Riconoscere se una frase data definisce un'insieme(*)
Passare da una rappresentazione all' altra dello stesso
insieme (*)
Riconoscere ed utilizzare le relazioni di appartenenza
ed inclusione(*)
Riconoscere e costruire unioni, intersezioni e
complementari di insiemi (*)
Utilizzare gli insiemi come modello per risolvere
problemi(*)
1. Aritmetica e algebra
Conoscenze
I numeri naturali,
operazioni e proprietà
interi,
razionali:
Abilità
definizioni, Riconoscere a quale insieme appartiene un numero
Ordinare e rappresentare i razionali sulla retta
Potenze a esponente intero e relative proprietà
Divisori e multipli di numeri naturali.
Riconoscere e utilizzare in modo opportuno le varie forme
di scrittura di un numero razionale (frazionaria, decimale,
percentuale)
Numeri primi, massimo comune divisore (MCD) e
minimo comune multiplo (mcm)
Confrontare numeri razionali
Riconoscere la struttura di un’espressione, numerica o
contenente parametri
I numeri irrazionali
Polinomi e relative operazioni
Operare in N, Z, Q, riconoscendo e applicando le proprietà
delle operazioni
Semplificare e calcolare semplici espressioni numeriche o
contenenti parametri, utilizzando le regole sulle priorità
delle operazioni e delle parentesi
Calcolare espressioni complesse utilizzando un calcolatore
elettronico(*)
Formalizzare e risolvere problemi, riconoscendo l’opportuno
universo e le opportune operazioni
Stimare, approssimare, valutare i risultati del calcolo
Distinguere i numeri razionali da quelli irrazionali
Operare con i polinomi, applicando le proprietà delle
operazioni tra numeri razionali
2 - Equazioni e disequazioni di primo grado
Conoscenze
Abilità
Proposizioni e formule aperte con predicato “essere Formalizzare un problema con un’equazione o una
uguale”, “essere maggiore”, “essere minore”
disequazione
Dominio di una formula aperta
Insieme delle soluzioni come sottoinsieme del dominio
Principi d'equivalenza
Risolvere equazioni e disequazioni intere di primo grado in
un’incognita
3 - Geometria euclidea del piano
Conoscenze
Il linguaggio geometrico: termini primitivi, assiomi
Ipotesi e tesi di un teorema
Rette, semirette, segmenti, angoli
Abilità
Utilizzare il linguaggio geometrico, distinguendo i termini
primitivi e gli assiomi, e formulando correttamente
definizioni ed enunciati
Utilizzare riga e compasso per costruire
corrispondenti a definizioni o descrizioni
figure
Triangoli, altezze, mediane, assi, bisettrici
Utilizzare la terminologia appropriata per descrivere figure
Criteri di congruenza dei triangoli
Individuare ipotesi e tesi di un teorema
Proprietà dei triangoli
Parallelismo e perpendicolarità
Circonferenze (in seconda)
Comprendere dimostrazioni e sviluppare semplici catene
deduttive(*)
Conoscere le proprietà dei triangoli, relativamente alla
congruenza
Poligoni regolari (in seconda)
Applicare le conoscenze geometriche alla risoluzione di
problemi in contesti diversi(*)
4 - Dati e previsioni
Conoscenze
Abilità
Dati: loro organizzazione
Raccogliere, organizzare e rappresentare un insieme di dati
Classificazione del carattere
Calcolare media, mediana, moda di un insieme di dati
Distribuzione delle frequenze a seconda del tipo di
carattere
Calcolare lo scarto dalla media di ciascun dato di un insieme
Rappresentazioni grafiche
Media aritmetica, moda, mediana
Campo di variazione, scarto semplice medio dalla media
aritmetica, scarto quadratico medio
Valutare quale tra due insiemi di dati, aventi la stessa media,
ha minore dispersione
Rappresentare un fenomeno statistico con un grafico
adeguato
Leggere e interpretare grafici rappresentanti fenomeni
statistici
CLASSI SECONDE
1 - Calcolo letterale
Conoscenze
Abilità
Prodotti notevoli
MCD e m.c.m. tra polinomi
Calcolare espressioni contenenti i prodotti notevoli
(a+b)(a-b); (a+b)2; (a+b)3
Scomporre in fattori espressioni contenenti i prodotti
notevoli
Scomporre in fattori espressioni del tipo a3+b3, a3-b3 (*)
Scomporre in fattori un trinomio di secondo grado del
tipo x2+sx+p
Calcolare il m.c.m. e il MCD tra polinomi
Calcolare e semplificare espressioni contenenti frazioni
algebriche(*)
2 - La retta nel piano cartesiano
Conoscenze
Abilità
Condizione d'appartenenza di un punto al grafico di
un'equazione
Determinare coefficiente angolare e ordinata all'origine di
una retta
Coefficiente angolare di una retta
Tracciare il grafico di un’equazione di 1° grado a due
variabili
Condizione di parallelismo e perpendicolarità
Scrivere l'equazione di una retta date due condizioni
Corrispondenza tra modello algebrico e modello
geometrico
Individuare il semipiano soluzione di una disequazione di
primo grado (*)
3 - Sistemi lineari e problemi con più condizioni
Conoscenze
Abilità
Sistema di formule
Formalizzare problemi con più condizioni
Insieme delle soluzioni di un sistema come intersezione
degli insiemi delle soluzioni delle singole equazioni
o disequazioni
Risolvere graficamente sistemi d'equazioni e disequazioni
in una o due incognite
Metodi di sostituzione e riduzione, metodo di Cramer(*)
Risolvere algebricamente sistemi d'equazioni utilizzando
il metodo più opportuno
4 - L'insieme dei numeri reali
Conoscenze
L'insieme dei numeri irrazionali
Abilità
Dimostrare che la radice quadrata di un numero che non
sia quadrato perfetto non è un numero razionale (*)
L'insieme dei numeri reali
Riconoscere e definire numeri razionali e irrazionali
Radicali aritmetici
Potenze a esponente razionale (*)
Semplificare un'espressione in cui compaiono radicali
quadratici
Trasformare radicali in potenze a esponente razionale e
viceversa (*)
Razionalizzare frazioni con radici quadrate al
denominatore(*)
5 – Relazioni e funzioni
Conoscenze
Abilità
Le funzioni e la loro rappresentazione (numerica,
funzionale, grafica)
Rappresentare sul piano cartesiano le principali funzioni
incontrate
Linguaggio degli insiemi e delle funzioni (dominio,
composizione, inversa, ecc.)
Studiare la funzione polinomiale di secondo grado
(rappresentazione grafica e ruolo dei coefficienti a, b, c)
Collegamento con il concetto di equazione
Funzioni di vario tipo (lineari, quadratiche, circolari, di
proporzionalità diretta e inversa)
Corrispondenza fra funzioni di secondo grado e parabola
6 - Equazioni e disequazioni
Conoscenze
Legge di annullamento del prodotto
Formula risolutiva dell'equazione di secondo grado
Abilità
Sulla base di una rappresentazione grafica determinare
l'esistenza e il tipo delle soluzioni reali di un'equazione
e di una disequazione(*) di secondo grado
Trovare algebricamente l'insieme delle soluzioni reali di
un'equazione di secondo grado applicando il metodo
di risoluzione più opportuno
Determinare l'insieme delle soluzioni di un'equazione di
grado superiore al primo applicando la legge di
annullamento del prodotto
7 – Geometria
Conoscenze
Abilità
Quadrilateri
Conoscere le proprietà delle principali figure piane e le
loro relazioni reciproche, relativamente a congruenza,
equiscomponibilità, equivalenza, similitudine
Circonferenza
Poligoni regolari
Applicare il metodo ipotetico-deduttivo per dimostrare
semplici teoremi e proprietà delle figure geometriche,
relativamente alle relazioni studiate
Equiscomponibilità ed equivalenza
Determinare l’area di figure piane e il volume di figure
solide, giustificando le formule
Area delle principali figure geometriche del piano
Aree e volumi delle principali figure geometriche nello
spazio(*)
Conoscere i teoremi di Euclide, di Pitagora e di Talete e
utilizzarli per risolvere problemi
Teoremi di Euclide; teorema di Pitagora
Teorema di Talete e sue conseguenze
Le principali trasformazioni geometriche e loro invarianti
(isometrie, similitudini(*))
8 – Dati e previsioni
Conoscenze
Abilità
Semplici spazi (discreti) di probabilità
Calcolare la probabilità di eventi elementari e di semplici
eventi composti
Eventi elementari ed eventi composti; eventi indipendenti
Significato della probabilità e sue valutazioni
Probabilità e frequenza
Avvertenza: l’asterisco * indica quelle abilità che non fanno parte dei minimi da raggiungere ai fini
della sufficienza
STRUMENTI
Verifiche scritte, interrogazioni orali, colloqui individuali.
LIBRI DI TESTO
BIENNIO “Amministrazione, finanze e marketing”
Classi prime (tutte le sezioni)
Bergamini, Trifone, Barozzi, Matematica con DVDROM – edizione VERDE vol.1 , ed. Zanichelli
Classi seconde (tutte le sezioni)
Bergamini, Trifone, Barozzi, Matematica con DVDROM – edizione VERDE vol.2 , ed. Zanichelli
BIENNIO “Chimica, materiali e biotecnologie”
Classi prime (tutte le sezioni)
L.Sasso, Nuova Matematica a colori – edizione VERDE, Algebra 1, ed. Petrini
L.Sasso, Nuova Matematica a colori – edizione VERDE, Geometria, ed. Petrini
Classi seconde sezioni A, B, D
L.Sasso, Nuova Matematica a colori – edizione VERDE, Algebra 2, ed. Petrini
L.Sasso, Nuova Matematica a colori – edizione VERDE, Geometria, ed. Petrini
Classe seconda sezione C
Andreini-Manara-Prestipino-Saporiti, Pensare e fare matematica – edizione MISTA, Algebra 2, ed. Etas
Andreini-Manara-Prestipino-Saporiti, Pensare e fare matematica – edizione MISTA, Geometria, ed. Etas
BIENNIO “Elettronica e elettrotecnica”
Classi prime (tutte le sezioni)
L.Sasso, Nuova Matematica a colori – edizione VERDE, Algebra 1, ed. Petrini
L.Sasso, Nuova Matematica a colori – edizione VERDE, Geometria, ed. Petrini
Classe seconda
L.Sasso, Nuova Matematica a colori – edizione VERDE, Algebra 2, ed. Petrini
L.Sasso, Nuova Matematica a colori – edizione VERDE, Algebra 1, ed. Petrini
BIENNIO “Informatica e telecomunicazioni”
Classi prime (tutte le sezioni)
Andreini-Manara-Prestipino-Saporiti, Pensare e fare matematica – edizione MISTA, Algebra 1, ed. Etas
Andreini-Manara-Prestipino-Saporiti, Pensare e fare matematica – edizione MISTA, Geometria, ed. Etas
Classi seconde (tutte le sezioni)
Andreini-Manara-Prestipino-Saporiti, Pensare e fare matematica – edizione MISTA, Algebra 2, ed. Etas
Andreini-Manara-Prestipino-Saporiti, Pensare e fare matematica – edizione MISTA, Geometria, ed. Etas
Cernusco S. N., 30/9/2012
DOCENTE
Severina Caroli
Roberta Frigerio
Cinzia Mandelli
Francesca Donadio
Laura Pasini
Antonella Ravera
Giuseppina Ferreri
Fulvia Avalle
Monica Terenghi
Franco Tornaghi
Francesca Berengo
Giuseppina Pizzoni
FIRMA