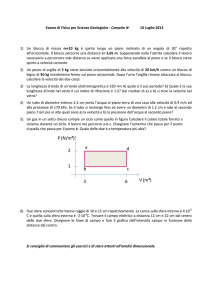
La sequenza
La rappresentazione
degli algoritmi
Diagrammi di flusso
Schemi di composizione fondamentali
Lo schema di sequenza è composto da più azioni
(non necessariamente elementari), che devono
essere eseguite una dopo l’altra, rispettando l’ordine
indicato dalle frecce.
!
La linea tratteggiata sta per “ci possono essere
ulteriori blocchi nella sequenza”.
2
La selezione
La selezione(2)
Lo schema di selezione permette invece di
selezionare un’azione da compiere in relazione al
fatto che una specifica condizione si verifichi o no. Lo
schema di selezione ha tre possibili varianti:
1. nel caso (a) se la condizione C è verificata è eseguita
un’azione A (non necessariamente elementare),
altrimenti non viene svolta nessuna azione;
!
2. nel caso (b) se la condizione C non è verificata è
eseguita un’azione A (non necessariamente
elementare), altrimenti non viene svolta nessuna
azione;
!
3. nell’ultimo caso (c) se la condizione C è verificata è
eseguita l’azione A, altrimenti l’azione B.
3
4
La ripetizione
La ripetizione(2)
Nello schema di ripetizione, una certa azione A vene
ripetuta fino a che non si verifica una certa
condizione C.
Lo schema di iterazione può presentarsi in quattro
modi: nei primi due a) e b), l’azione A può essere
eseguita zero o più volte, mentre negli altri due c) e
d) l’azione A è eseguita almeno una volta.
5
6
Esempio
SCARICARE DEI LIBRI DA UN FURGONCINO
Esempio (continua)
•
.
Nel caso (1) è stato utilizzato lo schema di ripetizione (d).
•
Consideriamo i due possibili diagrammi di flusso:
!
Osservare che in questo caso l’azione è svolta almeno una
volta; quindi, si dà per scontato che ci sia almeno un libro nel
furgoncino e, successivamente, finché il controllo registrerà la
presenza di libri da scaricare, si tornerà ad eseguire di nuovo
l’azione “scarica un libro”.
!
•
Nel caso (2) è stato utilizzato lo schema di ripetizione (b);
•
!
7
prima di svolgere qualunque azione, si esegue il controllo,
che potrebbe portare direttamente alla terminazione, senza
che l’azione sia stata svolta. In altre parole si tiene presente
l’eventualità che il furgoncino possa essere vuoto.
8
Esempio
Esempio(continua)
Viaggio verso New York
Abbiamo detto che con i tre schemi di base
(sequenza, selezione, ripetizione) è possibile
rappresentare qualunque azione complessa.
Vediamo come ciò può essere fatto considerando il
seguente caso per risolvere il problema “Andare a New
York”.
partiamo da uno schema generale composto da:
!
!
La tecnica è sempre la stessa: partiamo da uno
schema generale composto da:
9
10
Esempio(continua)
Se l’azione “Andare a New York” fosse elementare non ci
sarebbe altro da fare,
ma poiché andare a New York comporta una moltitudine di
altre azioni più semplici, cerchiamo di scindere le varie fasi
Potremmo, ad esempio, individuare innanzitutto una serie
di azioni da svolgere consecutivamente:
!
11
Esempio(continua)
Il blocco “Vai a Fiumicino”, per esempio, è costituito
da diverse fasi, come scegliere un mezzo di trasporto
ecc. Quindi, “esplodiamo” questo blocco facendo
alcune considerazioni: come ci vado a Fiumicino?
Con l’auto, ma possiedo un’auto? Se possiedo
un’auto dovrò prima fare benzina, e se invece non ho
l’auto dovrò andare in treno, ma prima devo fare il
biglietto, ecc. Rappresentiamo tutte queste azioni e
scelte attraverso lo schema mostrato di seguito.
12
Esempio(continua)
Programmazione strutturata
La programmazione strutturata consiste in una tecnica di costruzione dei
diagrammi di flusso per raffinamenti successivi: partendo da un unico blocco
che rappresenta l’intero problema da risolvere, andiamo a sostituirlo con uno
schema di composizione appropriato alle esigenze (sequenza, selezione,
iterazione), e così via fino ad ottenere esclusivamente azioni elementari.
Notiamo che dall’ ”esplosione” di un blocco rappresentante un’azione
complessa, otteniamo uno schema che ha sempre almeno un altro blocco
che rappresenta l’azione. Inoltre, ogni schema di composizione ha sempre e
solo un punto di entrata ed un punto di uscita.
Con un diagramma strutturato deve essere anche possibile effettuare
l’operazione inversa: partendo da uno schema esploso, si deve poter tornare
ad ottenere un singolo blocco rappresentante l’intero problema. Si deve
procedere semplicemente riconoscendo i vari schemi di composizione e
comprimendoli in blocchi più complessi, fino a giungere al blocco iniziale.
13
14
Esempio
Esempio(continua)
Böhm-Jacopini
I due schemi si equivalgono sotto il profilo della funzionalità,
ovvero rappresentano graficamente il flusso di controllo di
algoritmi equivalenti.
Vediamo ora il Teorema di Böhm-Jacopini in azione: a sinistra
abbiamo uno schema non strutturato ed a destra uno schema
strutturato equivalente
•
!
Il primo non è però strutturato, perché non è riconoscibile
nessuno degli schemi fondamentali di composizione.
!
Nel secondo, invece, possiamo riconoscere:
!
!
•
uno schema di sequenza (1);
!
•
uno di iterazione (2);
•
ed infine uno di sequenza (3).
15
16