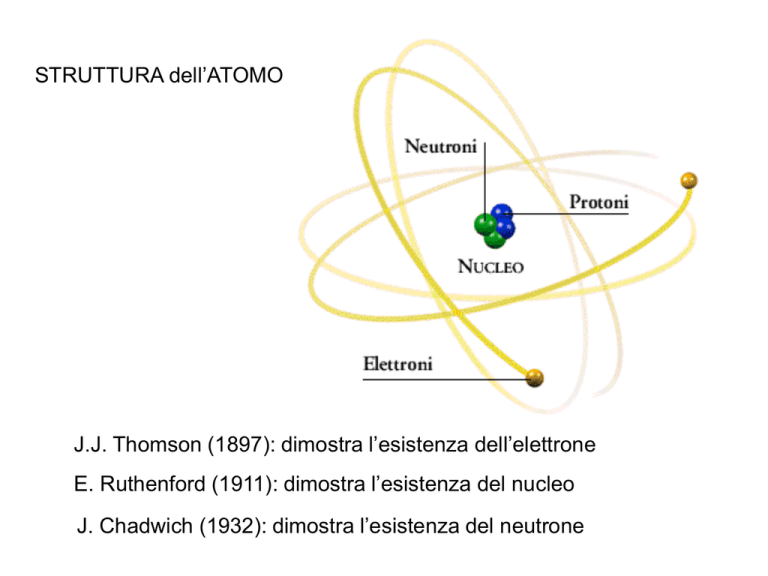
STRUTTURA dell’ATOMO
J.J. Thomson (1897): dimostra l’esistenza dell’elettrone
E. Ruthenford (1911): dimostra l’esistenza del nucleo
J. Chadwich (1932): dimostra l’esistenza del neutrone
J.J. Thomson (1897): dimostra l’esistenza dell’elettrone
raggi catodici:
He + n He+ + e-
e
E
2
m H r
Osservazione: il rapporto carica/massa dell’elettrone
è costante e indipendente dalla natura del gas.
e
1,76 1011coulomb kg 1
m
e = - 1,6 * 10-19 coulomb
R.A. Millikan: misura la carica dell’elettrone
m = 9,10 *10-31 Kg
E. Goldstein, Ruthenford (1907): scoperta del protone
raggi anodici:
He + n He+ + e-
Viene misurata la massa e la carica dello ione
positivo dell’atomo di idrogeno: “protone” (p+)
carica uguale e opposta all’elettrone
massa 1836 volte maggiore dell’elettrone
q = 1,602 * 10-19 C
m = 1,673 * 10-27 Kg
J. Chadwich (1932): dimostra l’esistenza del neutrone
particella priva di carica
q= 0
con massa simile al protone
m = 1,675 * 10-27 Kg
massa (uma)
1,00728
unità di massa atomica (u.m.a.) = 1,66 10-24 g
1,00867
0,000549
J.J. Thomson (1897): modello dell’atomo
Forma sferica con massa e carica positiva
uniformemente distribuita
Cariche negative uniformemente distribuite
L’atomo è elettricamente neutro.
E. Ruthenford (1911): esperimenti sul potere penetrante delle particelle a e
scoperta del nucleo
(particella a) = nucleo di elio
4
2
He2
polonio
Modello dell’atomo di Ruthenford (1911):
L’atomo è vuoto: Nel nucleo è concentrata tutta la massa e tutta la carica positiva.
Modello dinamico, planetario: Attorno al nucleo si muovono gli elettroni in numero
uguale alle cariche del nucleo.
L’atomo è elettricamente neutro.
In proporzione: diametro nucleo 1 cm - diametro atomo 100 m
Modello dell’atomo di Ruthenford (1911):
l’elettrone negativo ruota attorno al nucleo positivo, bilanciando l’attrazione
elettrostatica con la forza centrifuga
FCoulomb Fcentrifuga
q1q2 mv
k 2
r
r
2
meccanica classica: l’elettrone perde energia
emettendo radiazione elettromagnetica, rallenta il suo
moto e collassa sul nucleo.
Il modello contraddice le osservazioni sperimentali: l’atomo è
stabile
Spettrometro di massa: scoperta degli isotopi naturali
gli atomi vengono ionizzati a ioni positivi e deviati dal campo magnetico in
funzione della massa.
Percentuale isotopica
dell’antimonio
l’entità della deflessione dipende da
q/m
DIFETTO DI MASSA (Dm)
La massa di un nuclide è sempre inferiore alla massa che si ottiene
sommando le masse delle particelle che lo compongono.
4
2
He
massa teorica = 2(1,00728 uma) + 2(1.00867 uma) + 2(0.000549 uma) =
4,0329 uma
massa sperimentale = 4.0026 uma
Dm = 0.0303 uma
Il processo di formazione del nucleo a partire da protoni e neutroni libera
una grande quantità di energia, che rappresenta l’energia di legame (BE) del
nucleo.
Dall’equazione di Einstein si ricava che > è Dm >
energia occorre fornire per separare le particelle
del nucleo.
E = mc2
(BE) = (Dm)c2
BE = (0.0303 uma x 1,66*10-27kg)(2.99*108 ms-1)2 = 4.53*10-12J
BE per una mole di He (4 g) = 6,53 *108 kcal mol-1
Carta dei nuclidi
1
0
Elementi con Z < 20
Massima stabilità per N/Z = 1
4
2
He
n p
1
1
0
1
16
8
12
6
O
C
Elementi con Z > 20
Massima stabilità per N/Z = 11.5
120
50
Sn
200
80
Hg
206
82
Pb
1
p n
0
1
0
1
Radioattività: (Trasmutazione nucleare)
I nuclidi instabili (isotopi radioattivi) emettono spontaneamente particelle e/o
radiazioni elettromagnetiche, formando nuclei più stabili.
A
nuclide padre
B
+
particella
nuclide figlio
Tempo di
dimezzamento (t1/2):
caratteristico di ogni
sostanza è il tempo
in cui la quantità
iniziale di nuclei
radioattivi diviene la
metà
Elementi con T1/2
sufficientemente lungo
che possiamo trovare
in natura
Nuclide (A)
a, ,
Tipo di emissione
+
E
radiazione
Tempo di dimezzamento
Uranio 238
a
4.51 x 109 anni
Uranio 234
a
2.48 x 105 anni
Polonio 218
a
3.3 minuti
Polonio 214
a
1.6 x 10-4 secondi
Polonio 210
a
138,4 giorni
Piombo 214
26.8 minuti
Piombo 210
20.4 anni
Bismuto 214
19.7 minuti
Bismuto 210
5.0 giorni
Carbonio 14
5730 anni
tutti gli elementi con Z > 83 (bismuto) sono radioattivi
Metodo di datazione col radiocarbonio per organismi di 10000-20000 anni
12
6
C
stabile
C 147N 10e
t1/2=5730 anni
14
6
14
7
N n C H
1
0
14
6
14
6
12
6
C
C
1
1
Organismi vegetali e animali
O2
fotosintesi alimentazione respirazione
14
6
12
6
CO2
CO2
Il rapporto è costante negli organismi vivi
diminuisce nel tempo negli organismi morti
(S.I) La radioattività si misura in Becquerelle(Bq) = un decadimento al
secondo:
Bq = [s-1]
Struttura elettronica dell’ ATOMO
La quantizzazione dell’energia di Planck
Il modello atomico di Bohr
Il principio di indeterminazione di Heisenberg
La natura ondulatoria dell’elettrone
L’equazione d’onda di Schrödinger
Le forme e le energie degli orbitali
La configurazione elettronica degli atomi
RADIAZIONE ELETTROMAGNETICA: campo elettrico e campo magnetico
oscillanti, tra loro ortogonali, che si
propagano nello spazio.
Frequenza n = n° di
onde che passano per un
punto in un secondo
v
n
λ
Hertz (s-1)
La velocità delle onde elettromagnetiche che si
propagano nel vuoto (velocità della luce) è c:
c = 2.998 x108 m s-1
c ~ 300˙000 Km s-1
Spettro elettromagnetico: insieme delle onde elettromagnetiche a diverse
lunghezze d’onda
Max Planck (1901): la teoria dei quanti
L’energia non è una grandezza continua, essa viene emessa o assorbita
in quantità discrete, chiamate quanti.
Equazione di Planck
E hn
h = costante di Planck = 6,626*10-34 J s
L’energia di una radiazione è legata a quella del suo quanto.
L’intensità della radiazione dipende dal numero di quanti che costituisce una
radiazione.
La quantizzazione dell’energia non è rilevabile a livello macroscopico, ma si
osserva nei fenomeni su scala atomica.
Interazione materia-radiazione elettromagnetica
Le conoscenze sulla struttura degli atomi provengono da esperimenti di interazione
tra materia e radiazione elettromagnetica.
Una sostanza eccitata
emette radiazioni
elettromagnetiche
(spettro di emissione).
Una sostanza colpita
da una radiazione
elettromagnetica,
assorbe parte delle
radiazioni (spettro di
assorbimento).
Le frequenze emesse
o assorbite sono le
stesse.
Spettro di emissione dell’idrogeno
Equazione di Balmer
n2
C 2 2
n 2
n 3,4,5,6
Equazione di Rydberg
n
1 1
RH 2 2
n1 n2
1
n1 1,2,3,4,.....
n2 n1
RH = 2.180 x10-18J
Modello atomico di Niels Bohr (1913):
Primo postulato di Bohr: l’elettrone si muove su orbite circolari intorno al nucleo, sono
permesse soltanto le orbite per le quali il momento angolare dell’elettrone (mvr) è un
multiplo intero di h/2π .
h n = numero intero: 1,2,3,….
mvr n
2π
Secondo postulato di Bohr: L’elettrone non emette energia
quando si trova in una orbita permessa (stato stazionario).
L’atomo emette energia quando l’elettrone salta da un’orbita
più esterna a una più interna e la frequenza della radiazione
emessa è:
E2 E1 hν
Ei = energia dell’elettrone
nell’orbita i
Terzo postulato di Bohr: la carica del nucleo è “+Ze”. La carica dell’elettrone è “-e”
L’energia totale di un elettrone che si muove su orbita circolare a distanza r è
definita da:
1 2 Ze2
E E Cinet E Potenz mv
2
4 πε 0 r
Bohr calcola il raggio dell’orbita e l’energia dell’elettrone per l’idrogeno (Z=1)
FCoulomb Fcentrifuga
Ze2
mv 2
2
4 πε 0 r
r
ε0n h
r
πmZe2
2
nh
v
2 πmr
h
mvr n
2π
2
numero quantico
Raggio quantizzato
inserendo il valore della velocità (ricavata da (1)) e il raggio quantizzato (2)
nell’espressione dell’energia
(2)
r n 2 (0.53 1010 ) n 2a 0
quantizzazione momento angolare
n 1,2,3,4,.....
(1)
E, si ottiene:
2
1
Ze
2
E E Cinet E Potenz mv
2
4 πε 0 r
2
mZ 2e 4
RH
E
2
2 2
8 πε 0 n h
n
RH=2.179 x 10-18J
Energia quantizzata
r n a0
2
n = 2, 3, 4…stati eccitati
n=1
Stato fondamentale
corrispondente al
minimo di energia
RH
E 2
n
atomo di idrogeno
Ogni riga corrisponde
all’emissione di energia
associata a un salto da
E2 a E1
hv (E2 E1 )
RH
hn 2
n2
RH
2
n1
1
1
hn RH 2 2
n1 n2
Le frequenze calcolate con il modello di Bohr coincidono con le righe dello
spettro.
De Broglie (1924): la materia ha natura ondulatoria
Plank:I fotoni si propagano con moto ondulatorio e hanno energia E = hn
Einstein: I fotoni si muovono con velocità c e energia E = mc2
E hn
E mc2
n
hn mc2
c
h
c
mc
2
h
λ
mc
La radiazione elettromagnetica
(fotoni) ha natura corpuscolare
De Broglie estende il concetto a qualsiasi massa:
A qualunque particella di massa m, in movimento con
velocità v, può essere associata un’onda di lunghezza
d’onda
h
λ
mv
La materia ha natura ondulatoria
Dualismo onda-particella
La materia ha comportamento ondulatorio.
Per le particelle macroscopiche il comportamento ondulatorio può essere
trascurato e il moto può essere descritto dalle leggi della meccanica
classica
Per le particelle microscopiche (elettroni, protoni, e neutroni) occorre
tenere conto della natura ondulatoria.
Le particelle atomiche presentano caratteristiche ondulatorie o
corpuscolari a seconda del tipo di esperimento e strumentazione che
usiamo per osservarle.
PRINCIPIO DI INDETERMINAZIONE DI HEISENBERG (1926):
Non è possibile determinare esattamente e contemporaneamente la
posizione e la velocità di una particella.
h
ΔxΔp
4π
h
ΔxΔ( m v)
4π
h
ΔxΔv
4πm
p = momento della quantità di moto = mv
h = 6,626 * 10-34 J s
Se m è grande, l’incertezza Dv è trascurabile
Se m è molto piccola (massa dell’ e-)
l’incertezza su Dv è molto grande
m = 30,0 g, Dx = 1x10-3 cm
Dv = 1,7*10-26 cm s-1
me- = 9*10-28 g, Dx = 0.1Å = 10-9 cm
Dv = 5,8*108 cm s-1 = 5800 km s-1.
L’energia è quantizzata
Spettri atomici
Principio di Heisenberg
Natura duale della materia
(corpuscolare e ondulatoria)
Meccanica classica
Impossibile di conoscere
contemporaneamente posizione e
velocità di una particella
microscopica
Le particelle microscopiche
si comportano come onde
Meccanica quantistica
Non è possibile determinare la traiettoria dell’elettrone: si può parlare
solo di probabilità in una unità di volume
orbita
orbitale
EQUAZIONE di Erwin SCHRÖDINGER (1926)
Modello ondulatorio per l’elettrone dell’atomo di idrogeno: descrive il
moto di un elettrone attorno al nucleo come un’onda stazionaria.
2 πr nλ
n=5
n=6
Onda progressiva:
Onda stazionaria:
l’ampiezza in un punto
dipende dalla variabile tempo
l’ampiezza non dipende dalla variabile tempo
La lunghezza d’onda può assumere solo
determinati valori(le vibrazioni sono
quantizzate) 2 πr nλ
Equazione d’onda di Schrödinger
Il moto di un’onda è descrivibile tramite una equazione differenziale.
Schrödinger formula un’equazione differenziale per atomo di idrogeno le cui
soluzioni descrivono il moto dell’elettrone attorno al nucleo.
La funzioni d’onda (x,y,z) è funzione delle coordinate x, y, z dell’elettrone.
Esistono infinite funzioni d’onda (x,y,z) che sono possibili soluzione
dell’equazione. Per avere valore fisico deve soddisfare dei requisiti:
1) essere continua e finita
2) deve annullarsi all’infinito
3) devo assumere un solo valore in ogni punto
autofunzione
= funzione d’onda
descrive l’ampiezza
dell’onda in funzione delle coordinate spaziali,
quindi assume valori positivi e negativi. Non ha
significato fisico.
2 = funzione di probabilità
Ha valore sempre positivo o nullo e ha significato
fisico. E’ proporzionale all’intensità della
radiazione in un punto.
2 dV = Esprime la probabilità che un elettrone
si trovi in un infinitesimo volume dV.
Nel modello ondulatorio non si hanno distanze definite tra elettrone e nucleo
Orbita
orbitale
2s
Le funzioni d’onda (autofunzioni) sono caratterizzate da tre numeri quantici. Ogni
terna di numeri quantici definisce un’unica funzione, cioè un unico orbitale:
n
Numero quantico principale
energia
dimensioni
l
ml
Numero quantico secondario
forma
Numero quantico magnetico
orientazione in un
campo magnetico
nlm.
4pr2ψ2 = funzione di distribuzione radiale orbitale
4pr2ψ2dr = Probabilità di trovare l’elettrone in un guscio sferico di raggio r
e spessore dr
Il massimo della curva di probabilità radiale si ha per una distanza dal nucleo pari a
0.53 Å che corrisponde al raggio dell’orbita di Bohr (conferma la validità della teoria!)
La probabilità è diversa da zero anche a grandi distanze.
n = 2, l = 1, ml = 0, 1, -1
ORBITALI p
ORBITALI LOBATI
Ruotando il profilo di 180° si ottiene la
superficie limite tridimensionale
3 orbitali degeneri
211
210
21-1
l=2
ORBITALI LOBATI
ORBITALI d
ml = 0, 1, -1, 2, -2
5 orbitali
degeneri
322
321
320
32-1
32-2
IL NUMERO QUANTICO DI SPIN:
Ogni terna di numeri quantici n,
orbitale.
ms
l, ml
definisce un’unica funzione, cioè un unico
Il numero quantico di spin ms non è correlato agli altri tre.
Determina il momento angolare di rotazione di un elettrone (spin), immaginato come
una particella sferica ruotante attorno al proprio asse.
2 valori possibili per ms:
1
2
1
2
1
2
ATOMI POLIELETTRONICI
Ogni e- risente della repulsione di tutti
gli altri elettroni. Equazione d’onda più
complicata e di difficile soluzione.
Orbitali simili per forma e dimensioni
a quelli dell’atomo di idrogeno.
ATOMO DI IDROGENO (1 e-)
E
E
L’energia degli orbitali
L’energia degli orbitali
dipende solo da n.
dipende da n e da l.
CONFIGURAZIONE ELETTRONICA DEGLI ATOMI
PRINCIPIO DELL’AUFBAU (principio di costruzione)
Principio di esclusione di Pauli: due elettroni di uno stesso atomo non possono
avere identici valori dei quattro numeri quantici
n, l, ml, ms .
Regola di Hund: la configurazione di minima energia di un atomo è quella che
presenta il maggior numero di elettroni a spin parallelo
Gli orbitali vengono riempiti in ordine di energia crescente
Ogni orbitale può ospitare al massimo 2 e-, purché con diverso
valore di ms
L’accoppiamento di e- in uno stesso orbitale avviene dopo che
tutti gli orbitali degeneri contengono già un elettrone.
H (Z=1)
1s1
1s
He (Z=2)
1s2
1
ms
2
1s
Li (Z=3) 1s2 2s1
2s
2p
1s
Be (Z=4)
1s2 2s2
2s
2p
1s
B (Z=5) 1s2 2s2 2p1
2s
1s
2p
ms
1
2
• Regola di Hund: in un gruppo di orbitali degeneri, gli e- si dispongono singoli a
spin paralleli. L’accoppiamento di e- in uno stesso orbitale avviene dopo che tutti gli
orbitali degeneri contengono già un elettrone.
C (Z=6)
1s2
2s2
2p2
2s
2p
1s
N (Z=7)
1s2 2s2 2p3
2s
2p
1s
O (Z=8)
1s2 2s2 2p4
2s
1s
2p
4s ha energia minore di d
Cr 3d4 4s2
Cr 3d5 4s1
Configurazione più stabile
Periodicità della configurazione elettronica esterna
Periodi: Iniziano con configurazione s1 e terminano con configurazione esterna
completa “s2” (per He) o “s2 p6”. Tutti gli elettroni più esterni hanno stesso numero
quantico principale n. Il numero del periodo corrisponde a n.
Gruppi: uguale
configurazione
esterna (stesso
numero di elettroni
esterni con numero
quantico principale
crescente). Gli
elementi di un
gruppo hanno
proprietà chimiche
simili.
Proprietà periodiche
dimensioni atomiche (volume atomico, raggio atomico)
dimensioni ioniche
energia di ionizzazione
affinità elettronica
DIMENSIONI ATOMICHE: raggio atomico
La nube elettronica non ha un confine preciso a una certa distanza dal nucleo.
I raggi atomici sono ricavati misurando sperimentalmente le distanze tra i nuclei
di due atomi uguali nei solidi o nelle molecole gassose. Viene assunto pari alla
metà della distanza tra i due nuclei.
Nel sistema SI le dimensioni atomiche
sono espresse in nm
1 nm = 10-9 m
1 Å = 10-10 m
1 pm = 10-12 m
Zeff carica nucleare effettiva
ATOMI POLIELETTRONICI: Ogni e- risente della attrazione del nucleo e
della repulsione di tutti gli altri elettroni.
La carica nucleare effettiva (Zeff) che agisce su ogni elettrone è minore della carica
nucleare Z, poiché un elettrone esterno subisce l’attrazione di un nucleo schermato
dagli elettroni interni
Zeff = Z - S
S = costante di schermo
ogni elettrone dei livelli di energia superiori non ha effetto di schermo (S = 0)
per ogni elettrone dello stesso livello di energia S = 0.35
per ogni elettrone s o p del livello immediatamente inferiore S = 0.85
ogni elettrone dei livelli interni scherma un protone (S = 1)
K: Z = 19
1s22s22p63s23p64s1
Zeff sull’elettrone 4s1 = 19-(8 x 0,85)-(10 x 1) = 2,2
RAGGI ATOMICI
DEGLI ELEMENTI
(picometri = 10-12m)
Lungo un periodo: aumenta la carica nucleare Zeff;
aumentano gli elettroni del guscio esterno (gli e- dello stesso
guscio hanno scarso effetto di schermo). gli e- subiscono
maggiore attrazione verso il nucleo, r diminuisce.
Il raggio atomico aumenta
Lungo un gruppo:
aumenta il numero
quantico principale n,
l’effetto di scherno è
analogo, aumenta la
distanza dal nucleo, r
aumenta.
RAGGI IONICI DEGLI ELEMENTI
A An+
aumento della carica nucleare Zeff
A Andiminuzione della carica nucleare Zeff
contrazione volume
aumento volume
Energia di Ionizzazione (EI)
Energia da fornire per allontanare a distanza infinita uno degli elettroni
esterni di un atomo isolato allo stato gassoso.
A (g)
A+ (g) + e-
EI1
prima ionizzazione
A+ (g)
A+2 (g) + e-
EI2
seconda ionizzazione
EI2 >> EI1 : è più difficile allontanare un elettrone da un ione positivo
Il segno di EI è sempre positivo.
L’EI è una misura della forza con cui l’atomo lega l’elettrone.
Gli elementi con i valori più alti di EI sono i gas nobili
Gli elementi con i più bassi valori di
EI sono i metalli alcalini.
AFFINITA’ ELETTRONICA (AE)
Energia che viene ceduta da un atomo neutro isolato in fase gassosa quando acquista
un elettrone:
A (g) + e- A- (g)
Valori negativi di AE: (il sistema produce energia) tendenza dell’elemento ad
acquistare un elettrone spontaneamente.
Valori positivi di AE: (dobbiamo fornire energia al sistema) per l’elemento è difficile
acquistare un elettrone.
l’affinità elettronica diviene più negativa
(aumenta in senso assoluto) lungo un periodo
l’affinità elettronica diviene più negativa
(aumenta in senso assoluto) salendo lungo un
gruppo
H, metalli alcalini (I G) :
valori AE negativi piccoli
o positivi, non formano
anioni
Alogeni (VII G ) : valori AE negativi
elevati, formano facilmente anioni
F-, Cl-, Br-, I-









