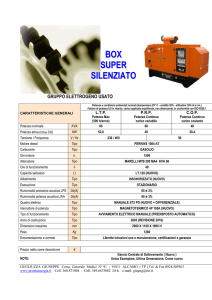
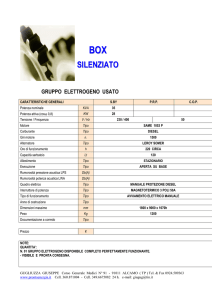
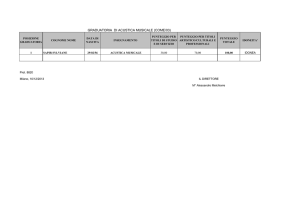
Acustica 1
Acustica 1
Cos’è il suono?
1
Lezioni di acustica
.
Il fenomeno sonoro e la sua descrizione elementare
Fabio Peron
Una perturbazione di carattere oscillatorio che si propaga in un mezzo elastico. Alla propagazione corrisponde una propagazione di energia ma non una propagazione di materia
Università IUAV - Venezia
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Acustica 1
2
Acustica 1
Sorgente: generatore di perturbazione, di vibrazioni
1.
Corpi solidi oscillanti: strumenti a corda
2. Colonne d’aria oscillanti: strumenti a fiato, organi
3. Corpi in rapido movimento: eliche, fruste
Perché si verifichi il fenomeno sonoro sono necessari:
4. Gas in rapida uscita da contenitori: razzi, reattori
5. Rapidi incrementi di pressione: esplosioni, detonazioni
Sorgente
⇒
Mezzo elastico
⇒
6. Voce umana: meccanismo 1+2
Ricevitore
Mezzo elastico: solido o fluido attraversato dalla perturbazione
ma non da essa modificato
• Il mezzo di maggior interesse pratico è l’aria
generatore di perturbazione, di vibrazioni
Solido o fluido attraversato dalla perturbazione
(il più importante per noi è l’aria)
• altri mezzi possono essere: la crosta terrestre, una parete, etc..
Qualcosa “sensibile” alla perturbazione
• il suono non si propaga nel vuoto
Ricevitore: qualcosa “sensibile” alla perturbazione
• un microfono
• una membrana
• l’orecchio umano
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
3
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
4
Acustica 1
Acustica 1
Sorgente: generatore di perturbazione, di vibrazioni
Ricevitore: qualcosa “sensibile” alla perturbazione
Il ricevitore fondamentale è l’orecchio umano sensibile solo a
perturbazioni caratterizzate da frequenze comprese tra:
20 Hz
infrasuoni
800 Hz
1
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Il mezzo elastico
5
Acustica 1
suono udibile
<
parlato
100
<
<
1000
10 000
20 kHz
ultrasuoni
8 kHz
Frequenza
[Hz]
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Onde e oscillazioni
6
Acustica 1
Il primo fenomeno oscillatorio osservato è stato la variazione
del livello della superficie del mare.
Si parla di onde tutte le volte che una grandezza varia
la sua entità nel tempo e nello spazio in maniera ripetitiva
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
10
<
7
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
8
Acustica 1
Onde e oscillazioni
Acustica 1
Onde e oscillazioni
L’oscillazione si propaga nel mezzo senza trasporto di materia
Le particelle oscillano intorno a posizioni di equilibrio
Il primo fenomeno oscillatorio osservato è stato la variazione
del livello della superficie del mare.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
9
10
Acustica 1
Acustica 1
Le grandezze che caratterizzano le onde
Le grandezze che caratterizzano le onde
periodo, T , [s]:
è il tempo che intercorre tra i passaggio in un determinato punto dello spazio
ampiezza
di due fasi omologhe dell’onda.
frequenza, f , [Hz]:
è il numero di oscillazioni complete che l’onda compie nell'unità di
ampiezza, A
tempo. Unità di misura sono i cicli per secondo ovvero gli hertz [Hz].
è l’entità della variazione della grandezza che oscilla
Essa corrisponde all’inverso del periodo:
lunghezza d’onda, λ , [m]:
è la lunghezza che intercorre tra due punti in cui in un certo istante si
1
T
velocità, c , [m/s]:
hanno fasi omologhe dell’onda.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
f =
è la velocità con cui la perturbazione si propaga nello spazio.
11
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
12
Acustica 1
Acustica 1
Tipi di onde
Le grandezze che caratterizzano le onde
Onde trasversali
frequenza angolare o pulsazione, ω, [rad/s] :
Onde longitudinali
per un oscillazione di tipo sinusoidale o cosinusoidale corrisponde all’angolo in
radianti descritto in un unità di tempo dal corrispondente oscillatore armonico.
ω =2π f
nota la velocità di propagazione dell’onda, c, valgono le seguenti relazioni tra
lunghezza d’onda, λ, pulsazione, ω, il periodo, T, e la frequenza, f, esistono
le seguenti relazioni:
f =
1
T
λ =
c
f
λ = c ⋅T
ω =2π f
T =
2π
ω
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
13
Acustica 1
Acustica 1
Tipi di onde
Onde longitudinali
14
Tipi di onde
Gas, liquidi, solidi
Onde trasversali
Solidi, corde
Onde flessionali
Barre, elementi piani
Onde di Rayleigh
Superfici dei solidi
Il moto di un mezzo pesante da origine alla propagazione di
diversi tipi di onda: superficiali, longitudinali e flessionali
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
15
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
16
Acustica 1
Acustica 1
Tipi di onde
fenomeni sismici: onde primarie, secondarie e di superficie
A. Primary Waves—are longitudinal waves or P waves. They move faster than other seismic waves and so arrive at distant point before other seismic waves.
C. Surface Waves— Lowe and Rayleightwaves ‐ P and S waves can be transformed into surface waves at Earth’s surface. Surface waves are a combination of longitudinal and transverse waves. Even though surface waves travel more slowly than P or S waves, they produce the most severe ground movements. B. Secondary Waves—are transverse waves or S waves. Secondary waves CANNOT travel through liquids. Since part of the earth is liquid, S waves do NOT travel directly through Earth and cannot be detected on the other side of Earth.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Comparison of wave animations with wave motion recorded
on seismograms
Map of west
central South
America showing
historical
seismicity (M6+,
1990-1999),
epicenter of
M6.5 earthquake
off the west
coast of Chile,
and location of
GSN
seismograph
station NNA
(Nana, Peru)
17
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Three-component seismograms for the M6.5 west coast
of Chile earthquake recorded at NNA
18
Acustica 0
Oscillazioni e moti armonici
Il fenomeno oscillatorio più semplice
è quello che si instaura quando un
corpo di massa m e attaccato ad una
molla di costante elastica K, viene
spostato
dalla
sua
posizione
di
equilibrio.
In conseguenza dello spostamento x sul corpo agisce una forza F,
responsabile di un’acellerazione sulla massa m secondo la legge di Newton:
F = -K x
F=ma
ma = - Kx
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
22
Acustica 0
Acustica 0
Si ottiene la equazione differenziale:
m
d 2x
dt 2
= −Kx
La soluzione di questa equazione differenziale fornisce la legge del moto che
corrisponde ad una oscillazione sinusoidale:
x ( t ) = A sen( ω t + ϕ )
con ω =
K
m
A = ampiezza
La velocità v(t) e l’accelerazione a(t) si ottengono derivando la relazione che
esprime lo spostamento x(t):
v (t ) =
Visivamente si può pensare di ottenere una rappresentazione del moto della
massa come riportato in figura.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
23
dx
= ωA cos(ωt + ϕ )
dt
a(t ) =
dv
= −ω 2 A sen(ωt + ϕ )
dt
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
24
Acustica 0
Onde sonore: perturbazioni di pressione
Acustica 1
Ai movimenti della massa sono associate anche variazioni della sua energia
cinetica, Ec, e della sua energia potenziale, Ee, (azione della molla).
Il fenomeno sonoro corrisponde ad una variazione oscillatoria di pressione. Le
diverse sorgenti sono dispositivi o fenomeni che sono in grado di indurre un
1
Ec = mv 2
2
E c (t ) =
1
mω 2 A 2 cos 2 (ωt + ϕ )
2
movimento oscillatorio alle particelle del mezzo considerato.
1
x
Ee = Kxdx = Kx 2
0
2
∫
E e (t ) =
1
KA 2 sen 2 (ω t + ϕ )
2
Poichè gli andamenti oscillatori di x(t) e v(t), che sono sfasati di mezzo
periodo, si deduce che l’energia cinetica è massima quando è minima quella
elastica e viceversa. L’energia totale rimane costante pari a:
E = Ec (t ) + Ee (t ) = cos tan te =
1
mω 2 A 2
2
Nel casa del mezzo aria, la sorgente sonora trasmette il moto alle particelle d’aria a
suo diretto contatto. Il moto vibratorio di queste particelle intorno ad una posizione
di equilibrio si trasmette ad altre adiacenti e la così la perturbazione si propaga nel
mezzo a distanze sempre più grandi.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Onde sonore: perturbazioni di pressione
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
25
Acustica 1
Onde sonore: perturbazioni di pressione
26
Acustica 1
Come strumento didattico consideriamo un pistone che si muove all’interno di un lungo condotto a pareti rigide. Esso genera un’onda piana di pressione ossia un onda sonora.
Min
Max
Pressione atmosferica
Pressione
[Pa]
Pressione MASSIMA
100 000
Pascal
Pressione atmosferica
Tempo
Pressione MINIMA
La sorgente sonora (es. un diapason) trasmette il moto alle particelle d’aria a
suo diretto contatto. Il moto vibratorio di queste particelle intorno ad una
Il fenomeno sonoro corrisponde ad una variazione oscillatoria di pressione. Le diverse
sorgenti sono dispositivi o fenomeni che sono in grado di indurre un movimento
oscillatorio alle particelle del mezzo considerato.
posizione di equilibrio si trasmette ad altre adiacenti e la così la perturbazione si
propaga nel mezzo a distanze sempre più grandi.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
27
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
28
Onde sonore: perturbazioni di pressione
Acustica 1
La superficie del pistone si muove di moto armonico semplice e
imprime lo stesso tipo di moto alle particelle di aria.
Spostamento:
s = so cos(ωt)
La variazione di pressione corrispondente al moto del pistone è
descritta dalla seguente relazione:
Pressione
p (x,t) = po sin (ωt - kx)
lunghezza d’onda, λ
s0
Acustica 1
Onde sonore: perturbazioni di pressione
pmin
pmax
Velocità di propagazione, c
so rappresenta il valore dello spostamento massimo della superficie del pistone.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Equazione generale dell’onda
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
29
Onde sonore: perturbazioni di pressione
Acustica 1
Acustica 1
Molecole d’aria
indisturbate
E’ importante conoscere al variare del tempo nei diversi punti dello spazio il
valore della perturbazione.
Per fare ciò si considerano i bilanci di massa, di energia e di quantità di moto
in un elemento infinitesimo
30
Periodo T
di volume dxdydz del mezzo in cui si propaga
Ampiezza A
l’onda.
Pmax
La propagazione dei gas si può rappresentare dalla combinazione di:
P0
equazione di Eulero (conservazione della quantità di moto)
Pmin
equazione di continuità (conservazione della massa)
equazione di stato termodinamico del fluido in esame.
Lunghezza
d’onda λ
∇2 p =
1 ∂2 p
⋅
c 2 ∂t 2
Massima compressione delle molecole d’aria
Equazione linearizzata dell’onda o
di D’Alembert
Molecole d’aria
in movimento
Minima compressione delle molecole d’aria
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
31
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
32
Acustica 1
Pressione acustica,
Onde sonore: perturbazioni di pressione
Δp, [Pa]:
si denomina pressione acustica la differenza tra la pressione in un
Pressione
[Pa]
punto nel mezzo attraversato dall’onda acustica e la pressione nello
stesso punto in assenza dell’onda.
Δ p = p – p0
New York
Pressione
atmosferica
In conseguenza delle variazioni di pressione si hanno variazioni di
densità per le quali si ha:
100 000
pascal
Δρ = ρ – ρ0
Mexico City
Le perturbazioni di pressione e di densità hanno valori molto limitati
Variazioni
Pressione
Sonora
rispetto ai valori medi delle due grandezze:
Δp
<< 1
p0
Δρ
ρ0
Acustica 1
<< 1
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
33
Acustica 1
Valori efficaci
Pressione sonora efficace RMS (Root Mean Square)
34
Acustica 1
Il sistema uditivo manifesta una sensazione sonora dipendente dal
E’ utile caratterizzare l’onda di pressione con valori sintetici che diano
un idea dell’effetto acustico.
contenuto energetico dell’onda è quindi necessario ricavare valori
rappresentativi del contenuto energetico. Questo si fa considerando i
Un’idea potrebbe essere quella di considerare i valori medi, ma una
funzione periodica presenta valori medi nulli, mentre il sistema uditivo
manifesta una sensazione sonora.
cosidetti “valori efficaci”.
D’altra parte utilizzare i valori massimi/minimi significa descrivere
solo l’ampiezza in un dato istante.
T
p =
1
[p(t )]2 dt
∫
T0
Per caratterizzare la perturbazione variabile di pressione legata alla
propagazione dell’onda si ricorre al valore efficace della pressione
noto come RMS sound pressure (Root Mean Square), che è un valore
sempre non negativo.
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
35
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
36
Acustica 1
Acustica 1
Velocità del suono nei fluidi
Riassumendo le grandezze che caratterizzano le onde sonore:
nota la velocità di propagazione dell’onda, c, valgono le
La velocità dell’onda acustica dipende essenzialmente dalla densità e dalla
deformabilità (modulo di Young) del mezzo.
seguenti relazioni tra lunghezza d’onda, λ, pulsazione, ω, il
periodo, T, e la frequenza, f, esistono le seguenti relazioni:
Gas
1
f =
T
c
λ =
f
λ = c ⋅T
ω =2π f
T =
⎛ p
k ⎜⎜ 0
⎝ ρ0
c =
2π
ω
Ammettendo
comportamento ideale:
Risulta allora:
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
pV = mR oT
c =
velocità del suono [m / s]
pressione atmosferica
cp / cv
densità del mezzo
p
da cui:
ρ
=
R oT
m
Ro : costante universale dei gas
m : massa
M : massa molare
T: temperatura termodinamica
kR oT
M
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
37
Acustica 1
Velocità del suono nei fluidi
c:
po:
k:
ρ 0:
⎞
⎟⎟
⎠
Velocità del suono nei solidi
38
Acustica 1
I Caso: Il solido è un corpo continuo, con sezione trasversale ampia rispetto
alla sezione longitudinale.
Un esempio: l’aria
Nel caso dell'aria in condizioni atmosferiche standard, 0°C e 101325 Pa, la
densità ρ è pari a 1.21 [Kg/m3].
c=
Essendo k = 1.4 e M = 29 kg/kmole si ottiene una velocità del suono pari a:
Y (1 − η )
ρ (1 + η )(1 − 2η )
[m\s]
Y : modulo di Young [ N/m2 ],
ρ: densità [Kg/m3],
co =
1 . 4 × 8314 × 273 . 15
= 331 ,1
29
η : rapporto di Poisson
[m\s]
II Caso: Il solido è una barra, cioè la sua sezione trasversale è piccola rispetto
alla sezione longitudinale e alla lunghezza d'onda.
A partire dalla velocità c0 a 0°C si può ottenere la velocità ad altre temperature:
In questo caso si può trascurare l’effetto laterale rappresentato dal rapporto di
Poisson, η:
c = co 1 +
t
≅ 331.4 + 0.6 t
273.15
c =
[m\s]
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
39
Y
ρ
[m\s]
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
40
Velocità del suono in diversi mezzi
Acustica 1
Velocità del suono in diversi mezzi
Acustica 1
Velocità del suono in mezzi diversi
materiale
aria
piombo
acqua
metacrilato
mattoni
legno
calcestruzzo
vetro
alluminio
acciaio
cartongesso
velocità del suono
m/s
rapporto rispetto
all’aria
344
1220
1410
1800
3000
3400
3400
5200
5200
5200
6800
1
3.5
4.1
5.2
8.7
9.9
9.9
15.1
15.1
15.1
19.8
Velocità del suono
in aria 20°C ≈ 340 m/s
Velocità del suono
in acqua distillata
c=
E
ρ
E = mezzo elastico ( N / m 2 )
ρ = densità ( kg / m 3 )
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
41
Università IUAV di Venezia - Acustica applicata e Illuminotecnica prof. F. Peron
42