Fisica ed Applicazioni degli Acceleratori
di Particelle
Corso di dottorato 2014
Fisica degli acceleratori di particelle
Parte I
Corso di dottorato 2014
Fisica degli acceleratori di particelle
Bibliografia parte I (Acceleratori di Particelle)
1.
2.
3.
4.
5.
6.
CERN 89-07 Yellow Report (sono spiegate abbastanza semplicemente le basi della
fisica degli acceleratori (è in francese))
Qualunque scuola CAS (Cern Accelerator School) in particolare CAS 2010 e CAS 2012.
Si trovano sul web le trasparenze cas.web.cern.ch/cas/CAS Welcome/Previous
Schools.htm e i proceedings cas.web.cern.ch/cas/Proceedings.html
Utili possono essere le slides che trovate al seguente indirizzo:
http://www.pd.infn.it/carlin/riv/Slides/Acc1.pdf e
http://www.pd.infn.it/carlin/riv/Slides/Acc2.pdf
Lezioni per gli studenti estivi al CERN
An Introduction to the Physics of Particle Accelerators. World Scientific, Mario Conte e
William W. MacKay
An Introduction to the Physics of High Energy Accelerators. John Wiley and Sons, D.A.
Edwards, M.J. Syphers.
Marisa Valdata Dottorato 2014
3
Fisica ed Applicazioni degli Acceleratori di Particelle
Introduzione
1.
Introduzione alla fisica degli acceleratori di particelle
•
•
•
•
•
•
•
•
•
2.
Introduzione
Sorgenti
Acceleratori a tensione continua
Acceleratori lineari
Acceleratori circolari
Anelli di Collisione
Oscillazione e stabilità dei fasci
Radiazione di sincrotrone
Raffreddamento dei fasci
Applicazione degli acceleratori di particelle
•
•
•
•
Applicazioni nella ricerca: fisica subnucleare, fisica nucleare, cosmologia ed
astrofisica, fisica atomica,scienza dei materiali, chimica e biologia
Analisi degli elementi e datazione dei reperti
Medicina: diagnosi e terapia
Applicazioni industriali (cenni)
Marisa Valdata Dottorato 2014
4
Fisica ed Applicazioni degli Acceleratori di Particelle
Introduzione
Gli acceleratori sono nati per lo studio della fisica nucleare e subnucleare.
Lo sviluppo della fisica delle particelle è direttamente collegato con la costruzione di acceleratori
di energia sempre più alta.
• Fine ottocento scoperta dell’elettrone con un tubo a raggi catodici (oscillografo, vecchio
televisore)
• Anni 50
scoperta dell’ p̄ al bevatron di Berkeley (sincrotrone a focalizzazione debole
di 6 GeV, accelerava p)
• Anni 60
scoperta del νµ all’ AGS di Brookhaven (AGS sincrotrone a gradiente
alternato accelera p a 33 GeV)
• Anni 70
Correnti neutre al PS del CERN (PS=protosincrotrone, accelera p di 28 GeV
è a focalizzazione forte)
• Anni 80
Scoperta del W e Z al Spp̄S del CERN (anello di collisione pp̄ del CERN,
costruito usando il Super Proto Sincrotrone (SPS) del CERN)
• Anni 90
Numero dei neutrini al LEP del CERN (anelli di collisione e+e- )
• Anni 2010
Scoperta dell’ Higgs ad LHC ( Large Hadron Collider, anelli di collisione pp
(ioni pesanti) al CERN di energia di progetto di 14 TeV nel CM )
Marisa Valdata Dottorato 2014
5
Fisica ed Applicazioni degli Acceleratori di Particelle
Introduzione
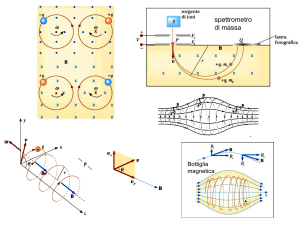
Il primo acceleratore è stato un tubo a raggi catodici:
Tubo a raggi catodici con cui Thomson scoprì l’elettrone
Marisa Valdata Dottorato 2014
6
Fisica ed Applicazioni degli Acceleratori di Particelle
Introduzione
L’acceleratore (anelli di collisione) ad energia più elevata è LHC
Marisa Valdata Dottorato 2014
7
Fisica ed Applicazioni degli Acceleratori di Particelle
Introduzione
Marisa Valdata Dottorato 2014
8
Fisica ed Applicazioni degli Acceleratori di Particelle
Progettazione di un acceleratore
Fisica degli acceleratori:
•
•
•
•
•
→
Cavità risonanti
Criogenia
Superconduttività
Progetto + costruzione magneti
Vuoto
Fisica delle superfici
Fisica dello stato solido
Elettrodinamica
Fisica dei fasci di particelle:
•
•
•
→
Dinamica della particella singola
Effetti collettivi
Interazioni fascio-fascio
Meccanica classica e quantistica
Dinamica non lineare
Relatività
Elettrodinamica
+ Ingegneria ed Informatica
Marisa Valdata Dottorato 2014
9
Fisica ed Applicazioni degli Acceleratori di Particelle
Utilizzo di un acceleratore
L’utilizzatore di un acceleratore è essenzialmente interessato ad alcune
caratteristiche degli acceleratori:
1.
2.
3.
4.
Tipo di particella accelerata.
Energia ed impulso delle particelle.
Intensità del fascio di particelle.
Fattore di utilizzo (duty cycle).
Marisa Valdata Dottorato 2014
10
Fisica ed Applicazioni degli Acceleratori di Particelle
Tipo di particella accelerata
• Particelle cariche uso di campi elettrici
• Particelle stabili p, p̄, e+, e-, ioni pesanti
• Si possono accelerare anche particelle cariche a lunga vita
media e.g. µ che vivono 2 µs
• Il tempo per accelerare le particelle è > 1s.
Marisa Valdata Dottorato 2014
11
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
L’ energia totale, l’impulso e l’energia cinetica di una particella di massa a
riposo m sono:
Energia Totale
W=γmc2
Impulso
p=βγmc
Energia cinetica K=W-Wr
(Wr=mc2)
La relazione fra energia ed impulso è:
𝑊 = √( 𝑝𝑝)2 + (𝑚𝑐 2 )2 = √ 𝑝2 + 𝑚2
Velocità relativistica (adimensionale)
Energia relativistica (adimensionale)
β=v/c
γ=1/√(1−β2)=1+W/Wr
_____________________________________________________________________________________________________________________
Le formule sovrascritte sono valide anche per nel caso non relativistico (β piccolo). Basta sviluppare in serie.
Nel caso ultrarelativistico (γ>>1) possiamo trascurare la massa a riposo m W≈K≈pc
Marisa Valdata Dottorato 2014
12
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
Marisa Valdata Dottorato 2014
13
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
Cosa ci insegna la cinematica relativistica e.g. per un elettrone?
La velocità cresce, ma non quanto l’energia.
Marisa Valdata Dottorato 2014
14
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
Utili possono essere le relazioni:
dW
2 dp
=β
W
p
_______________________________________________________________
dβ
1 dp
= 2
β
γ p
_______________________________________________________________
d (βγ ) = γ dβ =
3
dγ
β
_______________________________________________________________
Marisa Valdata Dottorato 2014
15
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
Normalmente si classificano le energie come:
γ≈1
non relativistico
γ>1
relativistico
γ>>1
ultrarelativistico
Le energie sono normalmente espresse in eV (o multipli KeV, MeV, Gev, TeV..)
1 eV=1.6x10-19J
e=carica unitaria=1.6x10-19C
Masse:
me=0.511 MeV/c2
mµ=105 MeV/c2
mp=938 MeV/c2
Marisa Valdata Dottorato 2014
16
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
L’impulso (energia) massimo raggiungibile dipende da:
Cavità acceleratrici (campo elettrico)
Raggio dell’acceleratore (acceleratori circolari)
Intensità dei campi magnetici (acceleratori circolari)
Marisa Valdata Dottorato 2014
17
Fisica ed Applicazioni degli Acceleratori di Particelle
Energia ed impulso delle particelle
Se accelero in una direzione la legge di Newton diventa
(relativisticamente) (slide 15):
dp
d ( βγ )
dβ
dv
dv
3
3
F=
= mc
= γ mc
=γ m
= m*
dt
dt
dt
dt
dt
la massa m * cresce come γ 3 volte la massa a riposo m
Marisa Valdata Dottorato 2014
18
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione
Forza di Lorentz
dp
=Q∗ E +v ×B
dt
(
)
Si guadagna energia solo con il campo elettrico
Potenziale scalare e vettore
1 ∂A
E = − grad Φ −
c ∂t
Campi elettrostatici
A=0
Campi variabili
Φ=0
Marisa Valdata Dottorato 2014
19
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione elettrostatica
L’energia finale è determinata dalla
tensione elettrica disponibile:
W=eV
Esistono quindi limiti tecnologici per
un generatore di tensione continua
(15-20MV)
Marisa Valdata Dottorato 2014
20
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione elettrostatica
I campi elettrostatici sono conservativi la differenza di potenziale V può
essere usata una sola volta.
Marisa Valdata Dottorato 2014
21
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
22
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
23
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
24
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
25
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
26
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
27
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
28
Fisica ed Applicazioni degli Acceleratori di Particelle
Accelerazione RF
Marisa Valdata Dottorato 2014
29
Fisica ed Applicazioni degli Acceleratori di Particelle
Campo magnetico uniforme
Per una particella di carica e in un campo magnetico uniforme:
dv
F = e v × B = γm
dt
Forza di tipo centrale con v = ω × ρ con ω costante e ρ raggio dell’orbita
(raggio di ciclotrone).
Se B è ortogonale a v allora:
p=βγmc=eBρ
Per una particella di carica pari a quella
dell’elettrone :
p(GeV/c)≈ 0.3B(T)ρ(m)
Marisa Valdata Dottorato 2014
30
Fisica ed Applicazioni degli Acceleratori di Particelle
Campo magnetico uniforme
Marisa Valdata Dottorato 2014
31
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Si distingue normalmente in:
• Flusso istantaneo, espresso normalmente in ppp (particelle
per impulso della macchina, cioè alla fine del ciclo di
accelerazione. (burst)
• Corrente media, carica accelerata per unità di tempo,
espressa in µA e mA e talvolta in pps (particelle al secondo).
Ad esempio l’ SpS ha una corrente media di 0.3 µA.
Marisa Valdata Dottorato 2014
32
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Burst e Bunch
Supponiamo di accelerare le particelle (fascio continuo) con dei campi elettrici
variabili nel tempo (sinusoidali) .
Le particelle che non sono in fase con quella sincrona (cioè quella che riceve la
giusta accelerazione), vengono in parte perse (almeno metà) ed in parte si
compattano vicino a quella sincrona. Le particelle si compattano in pacchetti
(bunch).
Alla fine di ogni ciclo di accelerazione estraggo un burst di particelle.
Marisa Valdata Dottorato 2014
33
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Bunch….
Se un fascio continuo di particelle entra
in una RF metà delle particelle vede il
campo con una fase sbagliata, poiché E
varia sinusoidalmente perdo metà
delle particelle
Consideriamo un sistema cavità RF, ed un
guadagno di energia eVs (linea tratteggiata).
Le particelle M1, N1, M2, N2 sono stabili
(sincrone), perché vedono sempre la stessa
fase del campo elettrico. La particella P che
arriva prima si trova E più piccolo e viene
quindi accelerata meno nel tubo
successivo arriva più vicina ad M2. La
particella P’, che arriva dopo viene
accelerata di più e nel tubo successivo
anch’essa sarà più vicina ad M2.
M1 ed M2 sono punti stabili per
l’accelerazione.
N1 ed N2 sono invece punti instabili in
quanto le particelle in Q’ e Q si allontanano
da N2 nel tubo successivo.
Particelle che entrano nel campo
elettrico nella fase discendente si perdono.
Marisa Valdata Dottorato 2014
34
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Nel caso di anelli di collisione ho normalmente dei fasci in
pacchetti (bunches).In alcuni punti un bunch colpisce un altro
bunch che si muove in senso opposto.
In questo caso più che di intensità dei fasci si parla di luminosità.
Per introdurre il problema consideriamo un fascio singolo che interagisce con
una targhetta lunga l e densa n2 particelle.
Per ogni particella del fascio
N=σintn2l
Se il fascio è di n1 particelle/s allora la velocità (rate) di conteggio è:
R=dN/dt=σintn2n1l=σintL
L= rate di interazioni per sezione d’urto unitaria (cm-2s-1)
Marisa Valdata Dottorato 2014
35
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
In un Collider importano:
• La densità dei fasci
• Le dimensioni e l’allineamento dei pacchetti
• L’angolo di incrocio
Per semplificare il caso consideriamo 2 singoli bunch che collidono fra loro ad
angolo 0.
La densità di particelle per unità di area nel piano trasverso sia distribuita
secondo una gaussiana identica per entrambi i bunch:
dn2
n2
e
=
ds 2πσ xσ y
2
2
− x
+y
2
2
2σ x
2
σ
y
Marisa Valdata Dottorato 2014
36
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
•
Il numero di particelle del fascio 1 in un elemento di area dxdy centrata in
x,y è:
dn1 ( x, y ) =
•
n1
e
2πσ xσ y
2
2
− x
+y
2
2
2σ x
2σ y
dxdy
La probabilità d’interazione di una particella del fascio 1 che si trova in x,y
p ( x, y ) =
n2
e
2πσ xσ y
2
2
− x
+y
2
2
2σ x
2σ y
∗ σ int
= numero di particelle del fascio 2 che si trovano in un area pari alla sezione
d’urto d’interazione.
Marisa Valdata Dottorato 2014
37
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Il numero totale di interazioni per bunch e per incrocio è:
N int = ∫ dn1 ( x, y )p( x, y ) =
+∞
n1n2
dxe
2 2 2 ∫
4π σ x σ y −∞
2
− x 2 + ∞
σx
∫ dye
2
− y 2
σy
−∞
=
n1n2
4πσ xσ y
Se abbiamo k pacchetti in ogni fascio (2 k punti di incrocio) e se f è la
frequenza di rivoluzione il rate per incrocio è:
R = σ int L =
L=
n1n2
4πσ xσ y k
f ∗ σ int
n1n2
4πσ xσ y k
Marisa Valdata Dottorato 2014
f
38
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Per cui:
L=
n1n2
4πσ xσ y k
f
Oppure usando le correnti i=nef
L=
i1i2
4πσ xσ y kfe
Marisa Valdata Dottorato 2014
2
39
Fisica ed Applicazioni degli Acceleratori di Particelle
Intensità del fascio di particelle
Nel caso di Luce di Sincrotrone si parla di Brightness e Brilliance.
• Brightness = numero di fotoni dn nell’intervallo di tempo dt
che passano nell’angolo solido dΩ diviso per lo 0.1% della
larghezza della banda dλ/λ.
d 4n
Φ Ω = 1000
dtdΩ dλ
( λ)
• Brilliance è la brightness per area S della sorgente
dΦ Ω
B=
dS
Marisa Valdata Dottorato 2014
40
Fisica ed Applicazioni degli Acceleratori di Particelle
Fattore di utilizzo
Il Fattore di utilizzo (Duty Cycle) è la frazione del tempo in cui le
particelle sono disponibili.
Se abbiamo a che fare con esperimenti su targhetta fissa ed
estraiamo il fascio dall’acceleratore ed il burst dura 1 s ed il ciclo
di accelerazione 10 s
Duty cycle=10%
Marisa Valdata Dottorato 2014
41