Università degli Studi di Milano Bicocca – Facoltà di Sociologia
Tecniche quantitative di analisi dei dati
Analisi della relazione fra due variabili quantitative
Esercizi svolti
ESERCIZIO 1
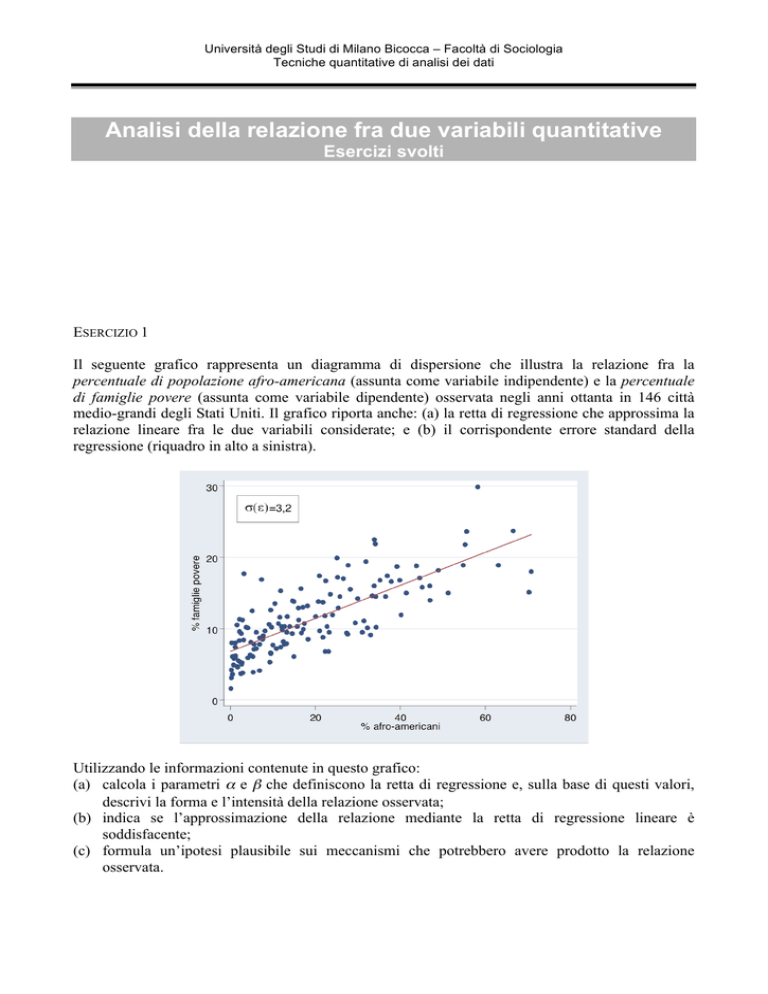
Il seguente grafico rappresenta un diagramma di dispersione che illustra la relazione fra la
percentuale di popolazione afro-americana (assunta come variabile indipendente) e la percentuale
di famiglie povere (assunta come variabile dipendente) osservata negli anni ottanta in 146 città
medio-grandi degli Stati Uniti. Il grafico riporta anche: (a) la retta di regressione che approssima la
relazione lineare fra le due variabili considerate; e (b) il corrispondente errore standard della
regressione (riquadro in alto a sinistra).
Utilizzando le informazioni contenute in questo grafico:
(a) calcola i parametri α e β che definiscono la retta di regressione e, sulla base di questi valori,
descrivi la forma e l’intensità della relazione osservata;
(b) indica se l’approssimazione della relazione mediante la retta di regressione lineare è
soddisfacente;
(c) formula un’ipotesi plausibile sui meccanismi che potrebbero avere prodotto la relazione
osservata.
Università degli Studi di Milano Bicocca – Facoltà di Sociologia
Tecniche quantitative di analisi dei dati
SVOLGIMENTO DELL’ESERCIZIO 1
(a) Aiutandoci con un righello, possiamo innanzitutto vedere che quando il valore della variabile
indipendente (asse orizzontale) è uguale a 0, il valore della variabile dipendente (asse verticale) è
circa uguale a 6,8. Pertanto, possiamo concludere che l’intercetta della retta di regressione è
approssimativamente uguale a 6,8; formalmente:
.
In secondo luogo, sempre aiutandoci con un righello possiamo vedere che quando il valore della
variabile indipendente passa da 20 a 40 (cioè aumenta di 20 unità), il valore della variabile
dipendente passa – all’incirca – da 12 a 16,5 (+4,5 unità). Ciò significa che per ogni incremento
unitario di X, il valore di y aumenta di circa (16,5-12)/(40-20)=4,5/20=0,23 unità. Pertanto,
possiamo concludere che l’inclinazione della retta di regressione è approssimativamente uguale a
0,23; formalmente:
. Questo valore ci dice che fra le due variabili prese in esame esiste una
relazione positiva, cioè all’aumentare dell’una tende ad aumentare anche l’altra. Più precisamente,
per ogni punto percentuale di famiglie afro-americane in più, la quota delle famiglie povere
aumenta di 0,23 punti percentuali.
Se calcoliamo il reciproco del parametro β, possiamo constatare che per avere un aumento di un
punto percentuale della quota di famiglie povere è sufficiente un aumento di 1/β=1/0,23=4,3 punti
percentuali della quota di famiglie afro-americane. Dunque, è legittimo concludere che l’intensità
della relazione fra le due variabili prese in esame è relativamente alta.
(b) L’approssimazione della relazione osservata fra X e y mediante la retta di regressione lineare
può essere valutata sulla base di tre criteri:
1. Valore assunto dall’errore standard della regressione: nel nostro caso questo valore
risulta uguale a 3,2. Poiché 3,2 corrisponde all’incirca a un settimo del campo di
variazione di y, possiamo concludere che – complessivamente – la capacità predittiva
della nostro modello di regressione lineare è apprezzabile ma non molto elevata.
2. Disposizione dei punti intorno alla retta: quando una relazione bivariata è lineare, per
tutto il campo di variazione di X il numero di punti sotto la retta di regressione tende a
essere uguale al numero di punti sopra la retta. Nel nostro caso le cose non stanno
esattamente così: per valori bassi di X ci sono più casi sotto la retta di regressione che
sopra di essa, mentre per valori intermedi di X ci sono un po’ più casi sopra la retta che
sotto di essa. Dunque, per approssimare in modo più soddisfacente la relazione osservata
fra X e y dovremmo disegnare una curva la cui inclinazione all’inizio è relativamente alta
ma poi tende a diminuire.
3. Presenza di casi influenti: il grafico mostra che esistono almeno due casi influenti. Il
primo tende ad attirare la retta di regressione verso l’alto, mentre il secondo tende ad
attirare la retta verso il basso. Complessivamente, dunque, l’influenza di questi due casi
dovrebbe annullarsi e non incidere in modo sostanziale sull’inclinazione della retta.
(c) Inserire interpretazione.
Università degli Studi di Milano Bicocca – Facoltà di Sociologia
Tecniche quantitative di analisi dei dati
ESERCIZIO 2
Il seguente grafico rappresenta un diagramma di dispersione che illustra la relazione fra il valore
aggiunto al costo dei fattori per abitante in milioni di lire (assunto come variabile indipendente) e il
numero di divorzi per 100.000 abitanti (assunto come variabile dipendente) osservata nel 1996-97
in Italia a livello regionale. Il grafico riporta anche: (a) la retta di regressione che approssima la
relazione lineare fra le due variabili considerate; e (b) il corrispondente errore standard della
regressione (riquadro in alto a sinistra).
Sulla base delle informazioni contenute in questo grafico:
(a) calcola l’inclinazione della retta di regressione (cioè il valore del parametro β del
corrispondente modello di regressione lineare semplice) e, sulla base di questo valore, descrivi
la forma e l’intensità della relazione osservata;
(b) indica se l’approssimazione della relazione mediante la retta di regressione lineare è
soddisfacente;
(c) formula un’ipotesi plausibile sui meccanismi che potrebbero avere prodotto la relazione
osservata.
Università degli Studi di Milano Bicocca – Facoltà di Sociologia
Tecniche quantitative di analisi dei dati
SVOLGIMENTO DELL’ESERCIZIO 2
(a) Aiutandoci con un righello, possiamo vedere che quando il valore della variabile indipendente
(asse orizzontale) passa da 20 a 30 (cioè aumenta di 10 unità), il valore della variabile dipendente
(asse verticale) passa – all’incirca – da 23 a 53 (30 unità). Ciò significa che per ogni incremento
unitario di X, il valore di y aumenta di circa (53-23)/(30-20)=30/10=3 unità. Pertanto, possiamo
concludere che l’inclinazione della retta è approssimativamente uguale a 3; formalmente:
.
Questo valore ci dice che fra le due variabili prese in esame esiste una relazione positiva, cioè
all’aumentare dell’una tende ad aumentare anche l’altra. Più precisamente, per ogni milione
aggiuntivo di valore aggiunto al costo dei fattori per abitante, il numero di divorzi per 100.000
abitanti aumenta di 3 unità.
(b) Un’attenta osservazione della figura mostra che l’approssimazione della relazione osservata fra
X e y mediante la retta di regressione lineare non è pienamente soddisfacente. Il problema non
risiede tanto nella dispersione dei casi intorno alla linea retta che, come testimonia anche l’errore
standard della regressione (
) è relativamente contenuta (in termini sostanziali, equivale a
circa un sesto dell’intera gamma di valori assunti dalla variabile dipendente). Il problema, piuttosto,
risiede nel fatto che la relazione osservata fra X e y non è esattamente lineare, ma tende a essere
leggermente curva verso il basso. Questo difetto di linearità è reso evidente dal fatto che nella prima
metà della “nuvola di punti” ci sono molti più casi sotto la retta di regressione che sopra di essa
(quando una relazione è tendenzialmente lineare, il numero di casi posti sotto la retta di regressione
e il numero di casi posti sopra la retta di regressione tendono a essere molto simili). Dunque, per
approssimare in modo più soddisfacente la relazione osservata fra X e y dovremmo disegnare una
curva la cui inclinazione all’inizio è relativamente bassa e poi, per valori di X maggiori di 25, tende
ad aumentare.
È anche opportuno osservare che la particolare posizione della Valle d’Aosta (in alto a destra) tende
ad “attirare” verso l’alto la retta di regressione, aumentandone l’inclinazione. In altri termini, la
Valle d’Aosta si configura come un possibile caso influente, cioè come un caso la cui presenza
influisce sulla stima dei valori dei parametri α e/o β del modello di regressione lineare semplice.
(c) L’esistenza della relazione bivariata fra “ricchezza” e “tasso di divorzio” discussa sopra può
essere interpretata in termini di effetto del benessere economico sul livello di stabilità della
famiglia. In generale, laddove c’è maggiore benessere economico le donne esibiscono livelli di
istruzione e tassi di partecipazione al mercato del lavoro più elevati rispetto alla media. Il possesso
di un elevato capitale culturale e le maggiori opportunità di lavoro rendono le donne
economicamente, culturalmente e socialmente più indipendenti dai mariti e quindi, a parità di
conflittualità coniugale, facilitano le separazioni e i divorzi. Si può anche pensare che nelle regioni
più ricche gli individui (uomini e donne) tendono a investire una quota relativamente elevata delle
proprie risorse temporali ed emotive nel lavoro, a discapito della cura delle relazioni familiari che,
pertanto, tendono a essere relativamente più deboli.










