SOLUZIONE PROVA SCRITTA 30 GENNAIO 2015
I Parte
Domanda 1 (5 punti)
Due liquidi di pari densità vengono fatti fluire lungo lo stesso piano inclinato. Nel primo
esperimento lo spessore del film di fluido 1, di viscosità µ1, è pari a δ1. Nel secondo esperimento lo
spessore del film di fluido 2, di viscosità µ2=100µ1, è pari a δ2=10δ1. Si determini quale dei fluidi
esibisce la portata volumetrica maggiore.
N.B. La risposta va motivata. In caso di sola risposta "secca" (1 o 2), anche corretta, verrà
attribuito punteggio zero.
Soluzione
A parità di tutte le altre condizioni (densità, angolo di inclinazione del piano), la portata volumetrica
è direttamente proporzionale al quadrato dello spessore e inversamente proporzionale alla viscosità.
In particolare si ha infatti:
Q=
W ρ g sin αδ 3
3µ
(1)
con ovvio significato dei simboli. Inglobando quindi nel coefficiente A tutti i termini costanti si può
quindi scrivere:
δ 13
Q1 = A =
µ1
δ3
Q2 = A 2
µ2
(2)
da cui:
3
3
Q1 ⎛ δ 1 ⎞ µ2 ⎛ δ 1 ⎞ 100 µ1 100
=
=
=
<1
Q2 ⎜⎝ δ 2 ⎟⎠ µ1 ⎜⎝ 10δ 1 ⎟⎠ µ1
1000
(3)
La (3) indica quindi che il fluido 2 esibisce la portata maggiore, in particolare dieci volte più grande
rispetto al fluido 1.
Domanda 2 (5 punti)
Scegliendo un esempio a vostra scelta, definite il numero di Sherwood, indicando con chiarezza il
significato di tutte le grandezze che lo compongono, e spiegatene il suo significato fisico e
ingegneristico.
Soluzione
Vedi ad esempio gli appunti del corso
II parte
Domanda 1 (10 punti)
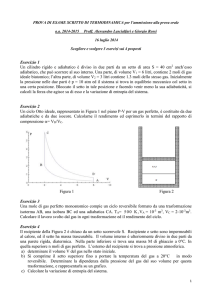
Un pallone aerostatico per rilievi metereologici di forma sferica e diametro D=2.5 m deve essere
predisposto per un lancio ascensionale. Il pallone ha una massa propria (quella del materiale che
costituisce l’involucro) pari a mp=7.5 Kg e viene riempito con elio (peso atomico PAHe=4). La
densità e la viscosità dell’aria atmosferica possono ritenersi costanti e pari rispettivamente ai
ρ=1.3Kg/m3 e µ=2⋅10-5 Pa s.
Si calcoli la pressione dell’elio all’interno del pallone, PHe(in atm) che garantisca una velocità
ascensionale, in condizioni stazionarie, pari a v∞=1.5 m/s. Si consideri comportamento da gas
perfetto per l’elio e si assuma trascurabile lo spessore dell’involucro. La temperatura è costante e
pari a 25°C.
La soluzione del problema consiste essenzialmente nella determinazione della massa di elio, mHe,
che garantisce la richiesta velocità ascensionale. Nota la massa, la pressione è immediatamente
calcolata dalla equazione di stato dei gas.
Il bilancio di forze sul pallone sancisce, in condizioni stazionarie, l’equilibrio della forza peso
(rivolta verso il basso), della forza di Archimede (rivolta verso l’alto) e della forza di drag tra l’aria
e il pallone (rivolta verso il basso). Scelto un asse verticale orientato (per esempio) verso il basso, il
bilancio assume la forma:
(
)
mp + mHe g −
π D3
ρ g + FD = 0
6
(4)
Dove FD è il modulo della forza di drag. La massa di elio viene dunque ricavata come:
F
π D3
mHe =
ρ − D − mp = 0
6
g
(5)
La forza di drag è sua volta calcolabile come:
FD =
cDπρ v∞2 D 2
8
(6)
Il coefficiente di attrito cD è ottenibile dalla correlazione con il numero di Reynolds, calcolabile in
quanto tutti i parametri che lo compongono sono noti.
Una volta determinata la massa di elio, la corrispondente pressione del gas è data da
mHe RT 6mHe RT
=
PAHeV PAHeπ D 3
(7)
ρ v∞ D 1.3⋅1.5⋅ 2.5
=
= 244000
µ
2 ⋅10−5
(8)
PHe =
Passando ai numeri si ha:
Re=
In tali condizioni si ha cD=0.44, per cui:
FD =
cDπρ v∞2 D 2 0.44 ⋅ π ⋅1.3⋅1.52 ⋅ 2.52
=
= 3.16N
8
8
FD
π D3
π ⋅ 2.53
3.16
mHe =
ρ+
− mp =
⋅1.3−
− 7.5 = 2.81Kg
6
g
6
9.81
(9)
(10)
e infine (occhio alle unità di misura per l’equazione di stato, con R=0.082 moli/L°K la massa è in
grammi e il volume in dm3!):
PHe =
6mHe RT 6 ⋅ 2810 ⋅0.082 ⋅ 298
=
= 2.10atm
PAHeπ D 3
4 ⋅ π ⋅ 253
(11)
Problema 2 (10 punti)
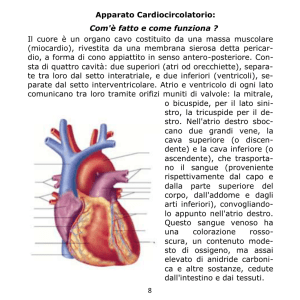
Un setto poroso di spessore δ=1mm separa due ambienti (vedi figura). L’ambiente di sinistra
contiene aria umida che, a sufficiente distanza dalla superficie del setto, può considerarsi satura
d’acqua. Quello di destra contiene aria che, a sufficiente distanza dalla superficie del setto, si può
considerare completamente secca. Il coefficiente di diffusione effettivo dell’acqua nel setto vale
Deff=0.15 cm2/s. Il coefficiente di scambio di materia convettivo per l’acqua in fase gas, sia a
sinistra che a destra, vale KC=5 cm/s. Sapendo che, alla temperatura di 50°C costante in tutto il
sistema, la tensione di vapore dell’acqua vale po=92.5 mmHg, e assumendo comportamento di gas
perfetto, si calcoli in condizioni stazionarie:
-­‐ La concentrazione in peso di acqua, wd (in g/L), sulla superficie destra del setto
-­‐ Il flusso di acqua, mw (in g/cm2 s) che attraversa il setto
w∞ = 0
w∞ = wsat
δ
Si tratta di un problema di trasporto di materia in serie in cui l’acqua viene trasportata dall’ambiente
di sinistra a quello di destra. Dette ws e wd le concentrazioni ponderali sulle due superfici del setto e
wsat quella di saturazione (che si realizza nell’ambiente di sinistra), il flusso di acqua può essere
espresso come:
mw = K C ( wsat − ws )
D
( ws − wd )
δ
mw = K C ( wd − 0 )
mw =
(12)
Le tre equazioni, espresse in termini di concentrazione e sommate membro a membro conducono
alla classica espressione del trasporto di materia in serie:
(w
sat
− ws ) =
mw
KC
(w − w ) = m
s
d
w
δ
D
m
wd = w
KC
⎛ 2
δ ⎞
wsat = mw ⎜
+ ⎟
⎝ KC D ⎠
(13)
da cui:
mw =
wsat
2
δ
+
KC D
(14)
Dalla (14) è possibile calcolare il flusso di materia. Rientrando con tale valore nella terza delle (13)
è possibile calcolare anche la concentrazione sulla superficie destra del setto. Il calcolo richiede
ovviamente la conoscenza della concentrazione di acqua on condizioni di saturazione. Ciò è
possibile utilizzando il comportamento da gas perfetto, per il quale vale la relazione:
p0 M w
wsat =
RT
(15)
dove Mw è il peso molecolare dell’acqua.
Passando ai numeri, la concentrazione di saturazione dell’acqua b(attenzione alle unità di misura!):
p 0 M w ( 92.5 / 760 ) ⋅18
g
g
wsat =
=
= 0.0827 = 8.27 ⋅10−5 3
RT
0.082 ⋅323
L
cm
(16)
Di conseguenza si ha:
8.27 ⋅10−5
g
mw =
=
= 7.75⋅10−5 2
2
δ
2 0.1
cm s
+
+
KC D
5 0.15
wsat
mw 7.75⋅10−5
g
wd =
=
= 1.55⋅10−5 = 0.0155
KC
5
L
(17)
(18)