VETTORE POSIZIONE E
VETTORE SPOSTAMENTO
!
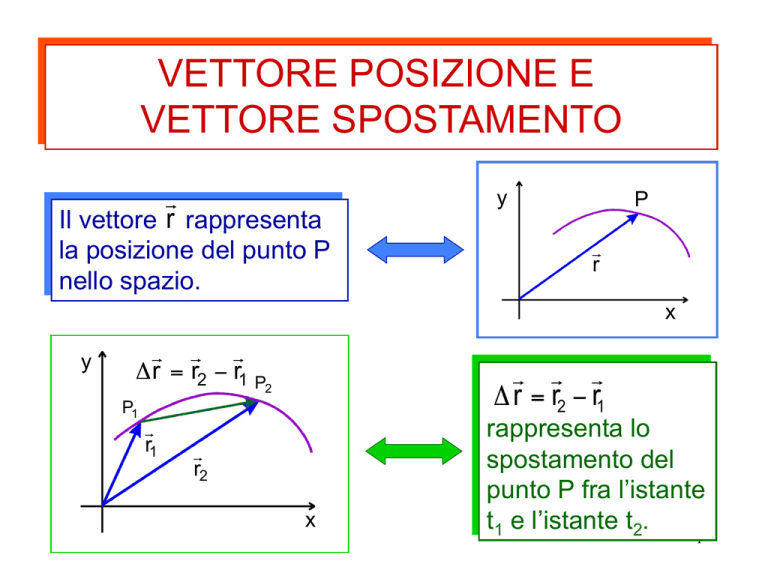
Il vettore r rappresenta
la posizione del punto P
nello spazio.
y
P
!
r
x
y
! ! !
Δ r = r2 − r1 P
! ! !
Δ r = r2 − r1
2
P1
!
r1
!
r2
x
rappresenta lo
spostamento del
punto P fra l’istante
t1 e l’istante t2.
1
VELOCITÀ VETTORIALE
La velocità vettoriale
del punto P è:
!
!
!
!
r2 − r1
Δr
v=
=
t 2 − t1
Δt
y
!
v
!
r1 !
r2
x
!
La velocità v rappresenta la velocità media nell’intervallo
(t1,t2). Quando l’ampiezza dell’intervallo Δt diventa molto
piccola (tende a zero), si ottiene la velocità istantanea
che è un vettore tangente alla traiettoria.
2
VELOCITÀ VETTORIALE
Le componenti della
velocità vettoriale lungo
gli assi di riferimento
rappresentano le velocità
dei punti proiezione sugli
assi x ed y.
y
!
vy
!
v
!
vx
x
Le proprietà della velocità esaminate nel piano (x,y) si
generalizzano al moto nello spazio rispetto agli assi x,y,z.
3
VELOCITÀ VETTORIALE
Y[m]
Δr
r
r’
traiettoria
X[m]
Come nel caso UNIDIMENSIONALE, se vogliamo il valore
istantaneo di velocità vettoriale dobbiamo considerare intervalli di
tempo molto piccoli.
Cioè:
vistantanea se Δtà0
STUDIAMO LA DIREZIONE
VELOCITÀ VETTORIALE
Y[m]
r
traiettoria
X[m]
La DIREZIONE del vettore vistantanea è quella della retta
tangente alla TRAIETTORIA nel punto considerato.
ACCELERAZIONE VETTORIALE
L’accelerazione vettoriale
del punto P è:
!
!
!
! v 2 − v1
Δv
a=
=
t 2 − t1
Δt
P1
!
v1
!
v1
!
v2
P2
!
v2
!
Δv
!
L’accelerazione a rappresenta l’accelerazione media
nell’intervallo (t1,t2).
6
ACCELERAZIONE VETTORIALE
Quando l’ampiezza
dell’intervallo Δt diventa
molto piccola (tende a
zero), si ottiene
l’accelerazione
istantanea.
y
!
v
!
a
x
L’accelerazione istantanea è sempre orientata verso la
parte concava della traiettoria.
L’accelerazione è nulla solo e soltanto quando il vettore
velocità è costante (moto rettilineo uniforme).
7
UNITÀ DI MISURA
!r # = !m#
" $ " $
!m#
!v # = % & = !m ⋅ s −1#
" $ s
"
$
" $
!m #
!m#
%
&
s = % & = !m ⋅ s −2 #
!a# =
" $ % s &
"
$
2
s
%"
&$ " $
8
MOTO RETTILINEO UNIFORME
Se la velocità vettoriale è costante il moto è rettilineo e
sono percorsi spazi uguali in tempi uguali, cioè gli spazi
percorsi sono proporzionali ai tempi impiegati.
Considerando l’asse x lungo la direzione del moto e
passando dai vettori agli scalari, si ottiene:
x = xo + v t
dove xo è la posizione iniziale (all’istante t=0).
Le variabili x e v sono numeri positivi o negativi, secondo
le convenzioni già stabilite.
9
MOTO RETTILINEO UNIFORME
Il moto rettilineo
uniforme è
rappresentato da
una retta nel grafico
spazio-tempo.
La pendenza della
retta è la velocità del
moto.
x
x2
α
x1
t1
t2
t
x 2 − x1
pendenza =
=v
t 2 − t1
10
MOTO RETTILINEO UNIFORME
velocità (m/s)
x = x o + vt
500
spazio (m)
Il moto rettilineo uniforme è
rappresentato da una retta
nel grafico spazio-tempo.
400
300
200
100
0
0
5
10
15
20
25
tem po (s)
30
20
10
0
0
5
10
15
tempo (s)
20
25
In tale moto, la velocità è
rappresentata da una retta
orizzontale nel grafico
velocità-tempo.
11
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
12
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
In un moto rettilineo con accelerazione costante lungo
l’asse x, la velocità è:
v = v o + at
Lo spazio percorso è dato da
x = xo + vmt
vo + v
1
vm =
= v o + at
2
2
1 2
x = x o + v o t + at
2
xo è la posizione iniziale (t=0)
vo è la velocità iniziale (t=0)
13
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
2500
spazio (m)
xo= 150 m
vo= 4 m/s
a = 10 m/s2
2000
1500
1000
500
0
0
5
10
15
20
25
velocita` (m/s)
250
200
150
100
50
0
0
5
10
tempo (s)
15
20
25
accelerazione (m/s^2)
tem po (s)
12
10
8
6
4
2
0
0
5
10
15
20
25
tempo (s)
14
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
spazio (m)
600
xo= 400 m
vo= - 75 m/s
a = 8 m/s2
500
400
300
200
100
0
0
5
10
15
20
25
velocita` (m/s)
100
50
0
-50
0
5
10
-100
15
20
25
accelerazione (m/s^2)
tempo (s)
10
8
6
4
2
0
0
tempo (s)
5
10
15
20
25
tempo (s)
15
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
400
200
spazio (m)
xo= 150 m
vo= 50 m/s
a = - 8 m/s2
0
-200
0
5
10
15
20
25
-400
-600
velocita` (m/s)
100
50
0
-50
0
5
10
-100
-150
tempo (s)
15
20
25
accelerazione (m/s^2)
tempo (s)
0
-2
0
5
10
15
20
25
-4
-6
-8
-10
tempo (s)
16
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
spazio (m)
1000
xo= 500 m
vo= - 4 m/s
a = - 12 m/s2
10
-100
-150
-200
-250
-300
tempo (s)
15
5
10
15
20
25
-1500
-2000
tempo (s)
20
25
accelerazione (m/s^2)
velocita` (m/s)
5
-500 0
-1000
-2500
0
-50 0
500
0
0
-2 0
-4
-6
-8
-10
-12
-14
5
10
15
20
25
tempo (s)
17
MOTO VERTICALE NEL
CAMPO DELLA GRAVITÀ
y
Fotografia stroboscopica di una
mela che cade; gli intervalli di
tempo sono uguali.
Un oggetto lasciato cadere da
una torre cade con velocità
crescente e copre distanze via
via maggiori ogni secondo.
18
MOTO VERTICALE NEL
CAMPO DELLA GRAVITÀ
y
(a) Una palla ed un leggero pezzo di
carta vengono lasciati cadere allo stesso
istante. (b) Ripetizione dell’esperimento
con la carta appallottolata
(a) Una pietra e una piuma
vengono lasciati cadere
simultaneamente (a) in aria,
(b) nel vuoto.
19
MOTO VERTICALE NEL
CAMPO DELLA GRAVITÀ
y
In vicinanza della
superficie terrestre tutti i
corpi si muovono con la
stessa accelerazione
g = 9.8 m/s2 = 980 cm/s2
1 2
y = v o t − gt
2
v = v o − gt
y
!
vo
!
g
x
20
MOTO VERTICALE NEL
CAMPO DELLA GRAVITÀ
Corpo lanciato verso l’alto:
raggiunge la massima altezza
h=hmax quando la velocità è nulla
(al tempo t=tmax).
v = v o − gt max = 0 ⇒ t max
hmax
vo
=
g
v o2
1 2
= v 0 t max − gt max =
2
2g
21
MOTO NEL
CAMPO DELLA GRAVITÀ
Le due sfere hanno velocità verticale iniziale nulla:
esse cadono in verticale con la stessa legge.
22
MOTO DI UN PROIETTILE
Se la velocità iniziale non è lungo la
verticale il corpo descrive una parabola.
La velocità orizzontale rimane costante,
mentre la velocità verticale varia.
23
MOTO DI UN PROIETTILE
Y
a = g = 9.8 m/s2
v0 θ
SUPERFICIE TERRESTRE
X
Un punto materiale ha velocità iniziale v0 inclinata
di un angolo θ sull’orizzontale.
Vogliamo determinare la traiettoria del punto materiale.
Si osserva che l’accelerazione è presente solo nella
direzione Y.
Scriviamo separatamente le equazioni orarie del punto
materiale su asse X ed asse Y.
Y
MOTO DEL PROIETTILE (2)
a = g = 9.8 m/s2
v0
θ
SUPERFICIE TERRESTRE
X
Che tipo di Equazioni orarie governano il moto
del punto materiale?
Su asse X non c’è accelerazione: equazione del moto
rettilineo uniforme.
Su asse Y c’è accelerazione g: equazione del moto
uniformemente accelerato.
Y
MOTO DEL PROIETTILE (3)
a = g = 9.8 m/s2
v0
v0y
θ
v0x
X
Si scompone la velocità iniziale secondo le
componenti X e Y.
v 0x = v 0 cosθ
v 0y = v 0senθ
Le due equazioni orarie
sono:
x = v 0x t
1 2
y = v 0y t − gt
2
Y
MOTO DEL PROIETTILE (4)
a = g = 9.8 m/s2
v0
v0y
θ
v0x
X
Dalle due equazioni orarie si elimina il
tempo e si ricava l’equazione della
traiettoria:
t=x/v0x
y = v0y x/v0x –g(x/v0x)2/2à
y = –(g/2v0x2)x 2 +(v0y/v0x)x
Equazione di secondo grado del tipo:
y = ax 2+bx+c
EQUAZIONE DI UNA…PARABOLA!
MOTO DEL PROIETTILE (5)
MOTO DEL PROIETTILE (6)
Dalle due equazioni orarie e dalla equazione
della traiettoria si possono ricavare molte
caratteristiche salienti sul moto.
1. Quanto tempo il proiettile resta in aria?
2. Qual è la massima altezza raggiunta?
3. A che distanza tocca Terra?
ESERCIZI (1)
Problema 1
Un sasso viene lanciato con una velocità di modulo pari a v = 17 m/s e con un angolo
di θ = 58° sopra l’orizzontale. Trascurando la resistenza dell’aria, determinare il tempo impiegato a raggiungere
la massima altezza. Soluzione
Nel punto di massima altezza la componente y della velocità
è nulla.
Se t* è il tempo impiegato a raggiungere la massima altezza:
Vy(t*) = 0
Ma Vy = V0y-gtà0 = V0y-g t* à t* = V0y/g = V0sen θ /g ESERCIZI (2)
Problema 1
Un aereo da soccorso vola ad una velocità v = 360 km/h alla quota
costante di h = 490 m. Quale distanza x, misurata sull’orizzontale, percorre
un pacco lasciato cadere dall’aereo?
Soluzione
La velocità iniziale ha SOLO la componente orizzontale, che rimane costante.
x= V0xt con V0x = 360 km/h E’ necessario determinare t* = tempo impiegato dal pacco a raggiungere
il suolo
y=h-gt2/2à 0=h-g t* 2/2 à t*2=2h/g à t* = (2h/g)1/2 x = V0x (2h/g)1/2










