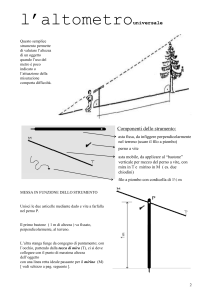
Capitolo 6: Divide et Impera
Divide et impera
Il termine divide et impera si basa su una massima antica dei tiranni, enunciata
anche da Machiavelli a proposito della politica dell’antico senato romano:
“ Per regnare, occorre tenere disuniti nemici e trarne vantaggio.”
Tuttora è la tecnica alla base della risoluzione di numerosi algoritmi e consiste
nel partizionare un problema in più sottoproblemi più piccoli dello stesso tipo.
Una volta risolti i singoli sottoproblemi, con poco sforzo, si ricombinano i
risultati parziali per ottenere la soluzione al problema originale.
Lo schema di una procedura ricorsiva DivideEtImpera
problema P
per risolvere un
di dimensione n è il seguente, dove k è una costante intera
prefissata:
procedure DIVIDEETIMPERA (P,n)
begin
if n ≤ k then
{ risolvi P direttamente }
else begin
{ dividi P in h sottoproblemi P1,…,Ph di dimensione
n1,…,nh };
for i := 1 to h do DIVIDEETIMPERA(Pi , n);
{ combina I risultati di P1,…,Pn per ottenere quello di P}
end
end
end;
56
Capitolo 6: Divide et Impera
Quicksort
Un tipico esempio della tecnica divide et impera è l’algoritmo del quicksort
inventato da Hoare nel 1962. Esso è l’algoritmo di ordinamento più veloce e
infatti il termine quick significa appunto svelto. La tecnica consiste nel
selezionare un elemento, detto perno, all’interno del vettore e nel spostare tutti
gli elementi minori dl perno alla sua sinistra e tutti quelli maggiori alla sua
destra. Lo stesso algoritmo va poi applicato alle due porzioni di elementi
maggiori e minori del perno.
La seguente procedura implementata in Pascal mostra un esempio dell’algoritmo
di quicksort.
procedure QuickSort(var A: vettore; iLo, iHi: integer);
var Lo, Hi, Pivot, T: Integer;
begin
Lo := iLo; Hi := iHi;
Pivot := A[Hi]; {Scelta del perno}
repeat
while A[Lo] < Pivot do Inc(Lo);
while A[Hi] > Pivot do Dec(Hi);
if Lo <= Hi then begin
T := A[Lo];
A[Lo] := A[Hi];
A[Hi] := T;
Inc(Lo);
Dec(Hi);
end;
until Lo > Hi;
if Hi > iLo then QuickSort(A, iLo, Hi); {Ordinamento parte minore del
perno}
if Lo< iHi then QuickSort(A,Lo,iHi); {Ordinamento parte maggiore del
perno}
end;
La chiamata nel programma principale sarà:
QuickSort(v, 1, n); dove v è il vettore da ordinare.
57
Capitolo 6: Divide et Impera
Bibliografia
- Alan Bertossi, Algoritmi e strutture di dati
Casa editrice UTET Libreria 2004
- http://www.wikipedia.org
58