27/10/2009
Statica e “momenti” delle
Forze
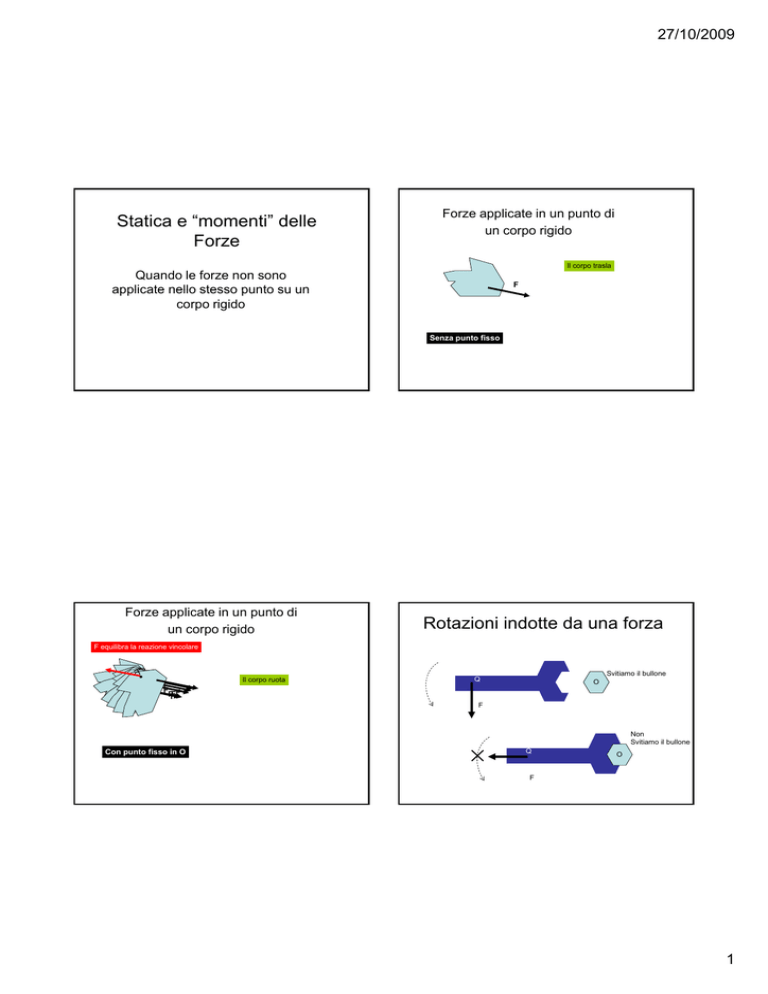
Forze applicate in un punto di
un corpo rigido
Il corpo trasla
Quando le forze non sono
applicate nello stesso punto su un
corpo rigido
F
Senza punto fisso
Forze applicate in un punto di
un corpo rigido
Rotazioni indotte da una forza
F equilibra la reazione vincolare
O
F
F F
FF
F
Il corpo ruota
Svitiamo il bullone
Q
O
F
Non
Svitiamo il bullone
Con punto fisso in O
Q
O
F
1
27/10/2009
Rotazioni indotte da una forza
E’ utile definire perciò
il momento di una forza
Svitiamo il bullone
Q
O
T = b Fp
F
O
b
Fp
Q
F
Conta la forza che esercitiamo perpendicolare
Alla direzione OQ.
Prodotto del “braccio” e della
Componente perpendicolare della
Forza alla direzione O-Q.
Cosa vuol dire “segno” del momento
di una forza?
Il momento T è un Vettore.
Segno del momento di una forza
T=Fb
T = b Fp
O
b
Fp
Q
L’osservatore vede un moto
antiorario: momento della forza >0
F
T>0
Se il momento è tale da indurre una
rotazione antioraria il momento
è considerato positivo
b
F
O
F
b
Fp
Q
T <0
2
27/10/2009
Cosa vuol dire “segno” del momento
di una forza?
Il momento T è un Vettore.
Baricentro o Centro di Massa
L’osservatore vede un moto
orario: momento della forza <0
F
b
T=-Fb
Centro di massa
Determinare il centro di Massa
Sinonimo di Baricentro
Il momento di tutte le forze peso rispetto a un punto di sospensione
È pari al momento del peso di un oggetto “puntiforme” con lo
Stesso peso totale.
O
O’
C.M
O
P2
P = P1+P2+P3 … +PN
C.M
O
P1
P
3
27/10/2009
Descrizione del moto di un corpo
rigido
Devo individuare un punto del corpo e
l’orientazione di un asse solidale con il
corpo
Rotazione di un punto intorno a un
asse
L’angolo θ individua la posizione
del corpo sulla circonferenza
Direzione di
riferimento
Si parla di
θ
Posizione Angolare
e di
Velocità Angolare, ω
Rotazione di un punto intorno a un
asse
Definizione di angolo in radianti
s2
Direzione di
riferimento
s
α
R2
R
Velocità angolare
θ
ω=
θ (t2 ) − θ (t1 )
(t2 − t1 )
4
27/10/2009
Legame fra la velocità angolare e
quella lineare
S
θ
S
S=θR
S=θR
θ
R
R
S’
R’=2R
θ
S
θ
ω=
S’ = θ R’
=2θR
=2S
Legame fra la velocità angolare e
quella lineare
R
Legame fra la velocità angolare e
quella lineare
v=
S (t1 , t2 )
(t2 − t1 )
θ (t2 ) − θ (t1 )
(t2 − t1 )
v = ωR
Esempio di moto angolare
v = ωR
V
Esempio:
Ruotiamo il braccio a una velocità
Angolare di un giro ogni due secondi.
R 0 75m
R=0.75m
R
La velocità angolare media è pari a:
ω=
1 Hz = 1 ciclo/s = 1 giro/s
2π
≅ 3.14 Hz
2s
Vext = Velocità lineare esterna: 2.3 m/s
R = 149.000.000 Km
ω=2π/365giorni=2x10-7 Hz
V = ω R = 149 x 109 m x 2 x 10-7 Hz
= 29800 m/s = 100000 Km/h
5
27/10/2009
moto di un corpo rigido
Traslazione di tutte le altre parti
del corpo con il centro di massa
e rotazione intorno a C
di tutte le altre parti del corpo
C
C
Centro di massa
Moto traslazionale
C
Rotazione
Intorno
AC+
Tralsazione
Del centro di massa
O
Rotazione
Intorno
aO
Silvia Rocca, Tesi di Laurea
Silvia Rocca, Tesi di Laurea
6
27/10/2009
Leggi della statica
traslazioni e rotazioni
Equilibrio per le rotazioni
FT
I momenti di tutte le forze devono equilibrarsi.
T1 + T2 + T3…. = 0
P
E’ equivalente a: la forza risultante sul corpo deve essere nulla:
F1 + F2 + F3…. = 0
P
P
Equilibrio con Forze non applicate
Allo stesso punto
Non basta dire che Ftot = 0
FT
P1 diverso da P2
b
b
FT
antiorario
b1
P
b2
orario
P
Ttot = b1 P1 – b2 P2 = 0
fulcro
O
Le equazioni di equilibrio sono:
Ftot = 0
Ftot = P + P + FT
Da cui:
Sono VETTORI!!!
Il “grassetto” indica
questo
Ttot = 0
Rispetto al Fulcro:
Ttot = bP - bP + 0 FT = b (P – P)
Ttot = b (P – P) = 0
La legge dei momenti torcenti
Rispetto a O è sempre
Ho equilibrio rotazionale
b1 P1 = b2 P2
P1
P2 = 3 P1
b1 : b2 = P2 : P1
Uguali braccia
Uguali pesi
E quindi:
La bilancia a Stadera
7
27/10/2009
Non importa il valore assoluto della lunghezza
Delle braccia della bilancia. Solo il loro rapporto!!
Equilibrio
b1 = 2 b2
b2
L1
maggiore asimmetria dei pesi
L1
maggiore asimmetria
della lunghezza delle braccia
P1
L2
L2
P1
P2 = 3 P1
P2 = 2 P1
La bilancia a Stadera
Altro esempio di proporzionalità diretta
b2 P1
=
b1 P2
P1
P2 = 3 P1
Altri modi di misurare il peso
La bilancia a due braccia
P
b2 = b1 1
P2
La bilancia a Stadera
8
27/10/2009
Altri modi di misurare il peso
Se effettuassimo delle misure…..
P2 = 5 P1
P2 = 3 P1
P1/P2
L2
L1
L2
1 cm
2 cm
3 cm
4 cm
5 cm
0.3 cm
0.7 cm
1 cm
1.2 cm
1.5 cm
1 cm
2 cm
3 cm
4 cm
5 cm
0.2 cm
0.4 cm
0.6 cm
0.8 cm
1.0 cm
=1
5
4
L2
L1
dipendono dal rapporto
3
= 0.5
= 0.3
2
1
0
Pendenze diverse
degli andamenti
rettilinei
0
1
2
3
4
P1/P2
5
L1
Altro esempio di proporzionalità diretta
Dipende dal punto in cui calcolo i momenti delle forze???
Come usare le Leve?
b2 P1
=
b1 P2
z
FT
Q
FT
Applichiamo le
Leggi della dinamica in Q
B
traslazione
b
B
F
O
P
Rispetto al fulcro O:
P⊥
Comp.
Perpend.
O
F⊥
b
b
F= P
B
F
-P + FT – F = 0
P
Comp.
Perpend.
Le forze sono proiettate lungo
L’asse z:
rotazione
Il momento della forza F rispetto a Q è nullo
P ·(b+B) – B·FT + 0 = 0
NB. Considero le forze e non le componenti perpendicolari al braccio per semplificare il diagramma
9
27/10/2009
esempio
Dipende dal punto in cui calcolo i momenti delle forze???
z
Centro di massa
Del braccio
Fm
FT
-P + FT – F = 0
Q
0.05m
P ·(b+B) – B·FT + 0 = 0
B
b
Reazione
Vincolare
Del gomito
F
O
E
0.15 m
0.2 m
Ps
P
P
FT = F + P
FT = F + P
P ·b + P · B = B·F + B· P
P ·(b+B) = B·FT
P ·(b+B) = B·(F+P)
P ·b = B·F
F = P ·b / B
Il braccio pesa circa 1.2 Kg, P = 12 N
La palla pesa circa 1.2 Kg, Ps = 12 N
Fm è la forza di richiamo del muscolo del braccio
Qual è la forza esercitata dal muscolo bicipite, Fm ??
NB. Considero le forze e non le componenti perpendicolari al braccio per semplificare il diagramma
Quanto vale la reazione vincolare del gomito???
esempio
Centro di massa
Del braccio
z
Fm =8.4 Kg
Fm =8.4 Kg
0.05m
G
P
Ps
Centro di massa
Del braccio
z
0.05m
G
G
0 5m
0.15
E = 6 Kg
0.2 m
0
P
E
Ps
Calcoliamo i momenti rispetto alla giuntura del gomito, G
0·E + 0.05 m · Fm - 0.15 m · P – 0.2 m · Ps = 0
0.05 m · Fm = 0.15 m · P + 0.2 m · Ps
0.15
0
5m
6Kg
0.2 m
0
P
Ps
Ftot = 0
-E – P – Ps + Fm =0
E = Fm – P – Ps = 84 N – 12 N – 12 N = 60 N
Fm = (0.15/0.05)· P + (0.2/0.05) · Ps
Fm = (0.15/0.05)· 12N + (0.2/0.05) · 12 N = 84 N
10
27/10/2009
Esempio 1
T è simmetrica a F
Dunque:
Tx = -Fx
Ty = Fy
Fy =
D
Fx =
P L
2 H
F 2 = Fx2 + Fy2
Fy
H
P
2
F
L
P
F2 =
2
Fx
2
L 2
1 +
H
Fx:F = L:D
L
Mtot =0=−P 2 +FyL
Ftot,x =0=Tx −Fx
F =0=T +F
x
y
tot,y
P
Fy = 2
Tx = Fx
T =−F
y
x
2
L PL
Fx = Fy =
H 2H
Se H Æ 0
Fx:Fy = L:H
2
2
P P L P L
F = F +F = + = 1+
2 2 H 2 H
2
x
F 2 = Fx2 + Fy2
2
y
e |T| = |F|
Fy H
=
Fx L
Esempio 2
2
2
P L
F 2 = 1 + → ∞
2
H
2
2
P2
P
P
F 2 = [1 + 1] = 2 =
2
2
2
Se H = L
Pedala… pedala…
Le forze sono inversamente proporzionali ai bracci
2F
F
2F
4F
5F
Le forze sono inversamente proporzionali ai bracci
11
27/10/2009
Leggi di conservazione
in Fisica
v0y
Ftot = ma
v0x
Ftot = m
(v2 − v1 )
(t2 − t1 )
equilibrio
Ftot =
Ftot = 0
X = x − x0 =
( mv2 − mv1 )
(t2 − t1 )
v0 x v0 y
g
( mv2 − mv1 )
=0
(t2 − t1 )
(v )
2
Y=
0y
2g
Leggi di conservazione
in Fisica
mv2 − mv1 = 0
mv2 = mv1
Conservazione della
quantità di moto
Quantità di moto = p = mv
( mv2 − mv1 )
=0
Ftot =
(t2 − t1 )
Per un SISTEMA di CORPI non soggetto a
forze o per cui le forze si equilibrano la
quantità di moto è costante
( mv2 − mv1 )
=0
(t2 − t1 )
mv2 − mv1 = 0
mv2 = mv1
12
27/10/2009
Ptotdopo = (m2 + m1 )v2
Ptotprima = m1v1
Ptotprima = Ptotdopo
m2
m1
m1v1 = (m2 + m1 )v2
v2 =
m1
(m2 + m1 )
v1
13












