Moto di una carica sotto l`azione di un campo elettrico uniforme Il

Lezioni di Fisica
Moto di una carica sotto l’azione di un
campo elettrico uniforme
Prof. Ettore Limoli
Il problema
Una carica q, di massa m, viene immessa con velocità v0 tra le armature di un condensatore piano. Il campo
elettrico E, all’interno del condensatore, deflette la carica che, uscita fuori dall’azione di E, colpisce uno
schermo posto a distanza D dal condensatore. Nota la lunghezza ℓ delle armature, la distanza d tra le
armature, la tensione V tra esse, si determini il punto dello schermo che viene colpito.
Approccio risolutivo
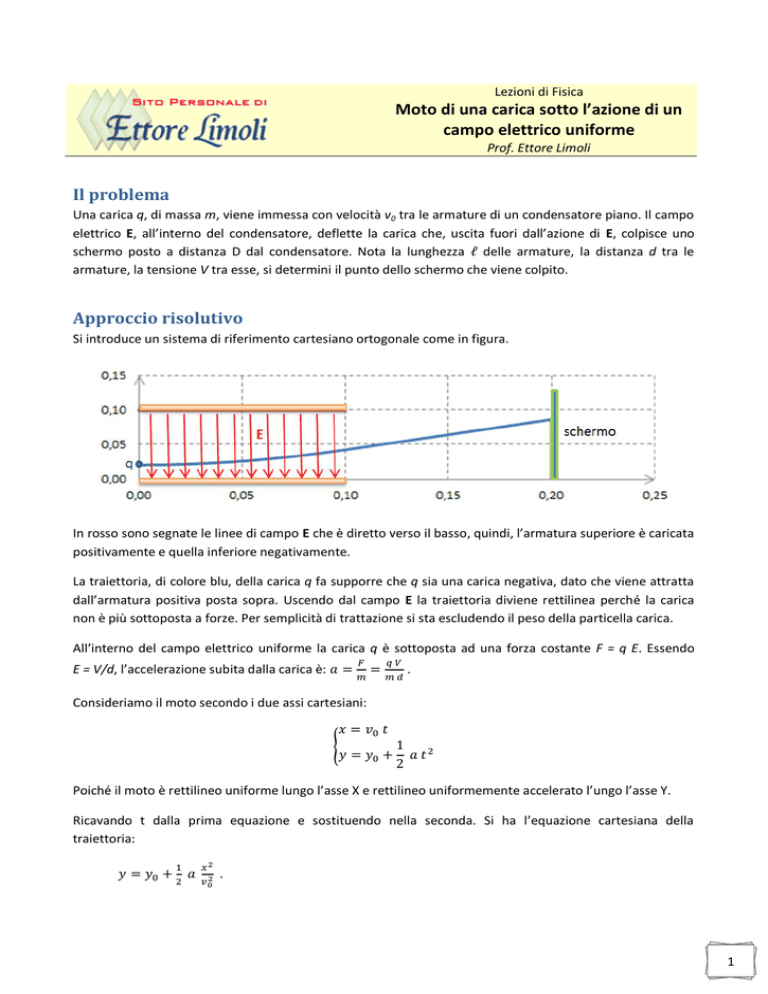
Si introduce un sistema di riferimento cartesiano ortogonale come in figura.
In rosso sono segnate le linee di campo E che è diretto verso il basso, quindi, l’armatura superiore è caricata
positivamente e quella inferiore negativamente.
La traiettoria, di colore blu, della carica q fa supporre che q sia una carica negativa, dato che viene attratta
dall’armatura positiva posta sopra. Uscendo dal campo E la traiettoria diviene rettilinea perché la carica
non è più sottoposta a forze. Per semplicità di trattazione si sta escludendo il peso della particella carica.
All’interno del campo elettrico uniforme la carica q è sottoposta ad una forza costante F = q E. Essendo
E = V/d, l’accelerazione subita dalla carica è: 𝑎 =
𝐹
𝑚
=
𝑞𝑉
𝑚𝑑
.
Consideriamo il moto secondo i due assi cartesiani:
𝑥 = 𝑣0 𝑡
{
𝑦 = 𝑦0 +
1
𝑎 𝑡2
2
Poiché il moto è rettilineo uniforme lungo l’asse X e rettilineo uniformemente accelerato l’ungo l’asse Y.
Ricavando t dalla prima equazione e sostituendo nella seconda. Si ha l’equazione cartesiana della
traiettoria:
𝑦 = 𝑦0 +
1
2
𝑎
𝑥2
𝑣02
.
1
Si tratta quindi di una parabola. Si noti che E ha segno negativo essendo diretto in direzione opposta
all’orientamento dell’asse Y. Se la carica è negativa a sarà positiva e la parabola volgerà la concavità verso
l’alto.
Nel punto di ascissa 𝑥 = ℓ il campo E cesserà la sua azione e la carica proseguirà seguendo la tangente alla
parabola in detto punto.
𝑎
𝐴= 2
2𝑣0
Posto: {
, l’equazione della parabola diventa: 𝑦 = 𝐴𝑥 2 + 𝐵. L’equazione della tangente è:
𝐵 = 𝑦0
𝑦 − (𝐴ℓ2 + 𝐵) = 2𝐴ℓ(𝑥 − ℓ)
Dove il coefficiente angolare è dato dalla derivata prima calcolata nel punto di ascissa ℓ. Ponendo a sistema
con la retta 𝑥 = ℓ + 𝐷, che è l’equazione dello schermo, otteniamo l’ordinata del punto colpito:
𝑦 = (𝐴ℓ2 + 𝐵) + 2𝐴ℓ(ℓ + 𝐷 − ℓ) = 𝐴ℓ2 + 2𝐴ℓ𝐷 + 𝐵.
Ovviamente, si è supposto che la carica attraversi tutto lo spazio interno fra le armature senza urtarle.
Questo, chiaramente, dipende dai dati iniziali del problema.
Esempio
Un elettrone, carica q = -1,610-19 C, massa m = 9,110-31 kg, viene immesso tra le armature del
condensatore a distanza y0 = 0,02 m dall’armatura inferiore con velocità iniziale v0 = 1,5106 m/s. Il
condensatore ha le seguenti caratteristiche: ℓ = 0,10 m; d = 0,10 m; V = -10 V. Alla tensione diamo valore
negativo perché il campo E è diretto nel verso opposto agli assi.
Lo schermo viene posto a distanza D = 0,1 m, pertanto, nel nostro riferimento, sarà la retta di equazione
x = 0,2.
Eseguiamo i calcoli con l’ausilio del foglio elettronico.
La zona con sfondo grigio riporta i valori calcolati mediante formule, le altre zone riportano i dati del
problema.
2
(*) Un valore negativo di
V indica un opposto
orientamento del campo
rispetto all’asse Y.
I nomi assegnati sono:
Le formule sono le seguenti
Il grafico della traiettoria è stato ottenuto con lo stesso foglio elettronico tabulando la traiettoria. Per
semplicità di trattazione questo calcolo è stato omesso.
3
Il punto colpito ha coordinate (xS, yS).
Nel calcolo di yS è stata usata la funzione SE() perché non è detto che i dati iniziali consentono alla carica di
attraversare il condensatore.
L’uso dello schema di calcolo col foglio elettronico ci consente di variare i dati del problema e vedere cosa
succede. Ad esempio, se riduciamo la velocità iniziale v0 potrebbe essere colpita l’armatura e avere yS = d.
Prof. Ettore Limoli
4