Grandezze scalari e vettoriali
Distanza, massa, temperatura ecc. sono completamente definite da 1 numero (+ un. misura).
Sono grandezze scalari
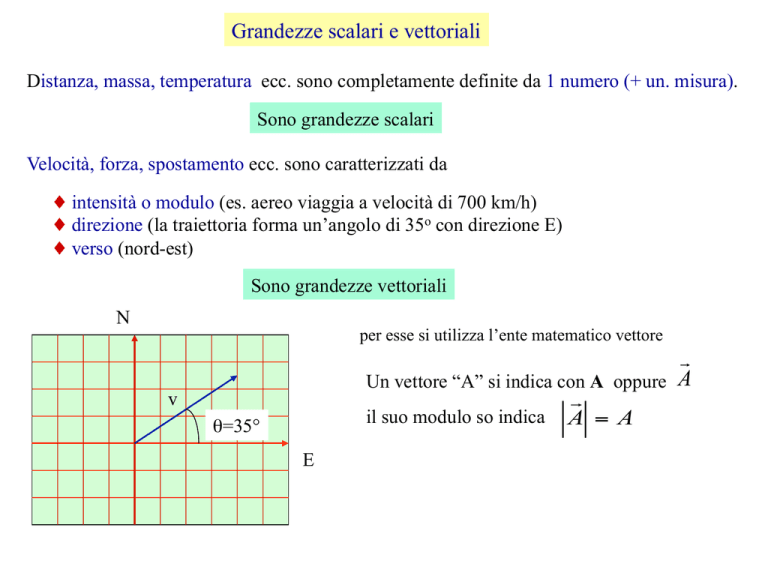
Velocità, forza, spostamento ecc. sono caratterizzati da
♦ intensità o modulo (es. aereo viaggia a velocità di 700 km/h)
♦ direzione (la traiettoria forma un’angolo di 35o con direzione E)
♦ verso (nord-est)
Sono grandezze vettoriali
N
per esse si utilizza l’ente matematico vettore
Un vettore “A” si indica con A oppure A
v
il suo modulo so indica
θ=35°
E
A = A
Rappresentazione di un vettore
Ad es. Il vettore posizione OP in un piano (2D) Graficamente: segmento orientato (freccia)
P
a
θ
O
modulo
$
a
• lunghezza OP ( a=|a| )
• angolo orientato rispetto
ad una retta data
direzione
e verso
(rappresentazione in coordinate polari)
In alternativa:
• Componenti X e Y rispetto ad un sistema di
assi cartesiani (coordinate cartesiane)
y
$
aY
O
P
aX, aY sono le “componenti cartesiane” di a
a
$
aX
Relazione fra le 2 rappresentazioni
x
$!a X = a cos θ
#
!"aY = a sin θ
$a = ( a 2 + a 2 )
!
X
Y
#
!"tan θ = aY a X
Vettori
z
caso 3D!
Az
φ
A
Ax
Ay
y
In 3D, servono 3 componenti:
3 componenti cartesiane: Ax, Ay, Az
oppure
modulo + 2 angoli: A, θ, φ
θ
x
Terna cartesiana destrorsa.
Axy
Trasformazione coordinate cartesiane / coordinate polari
$ A X = Asin φ cosθ
&
% AY = Asin φ sin θ
& A = Acos φ
' Z
$ A = (A 2 + A 2 + A 2 )
X
Y
Z
&&
%cos φ = AZ A
&tan θ = A A
&'
Y
X
Due vettori sono uguali <=>
• sono uguali modulo, direzione e verso
• sono uguali le componenti X, Y, Z
Operazioni con i vettori
a
B
b
C
prodotto scalare
prodotto per uno scalare
prodotto vettore
Somma
Dati i vettori AB e BC
c
A
Il vettore AC
si dice somma di AB e BC
a
A
somma (differenza)
B
b
c
C
AB + BC = AC
a +b = c
Regola del parallelogramma
Questa regola riproduce anche la somma di
due forze, due velocità ecc.
Disuguaglianza triangolare:
a −b ≤ c ≤ a +b
Somma di vettori
a
A
b
B
$
aX
C
Spesso conviene usare le componenti cartesiane:
a +b = c
c
$
$c X = a X + b X
!
!
#cY = a Y + bY
!
!
"c Z = a Z + b Z
bX
Somma di più vettori:
€
A2
6
A4
A5
A3
S=
A6
A1
S
∑ AK
6
K =1
SX = ∑ A KX
K =1
6
SY = ∑ A KY
K =1
6
€
Rappresentazione grafica
SZ = ∑ A KZ
K =1
Somma di vettori. Proprietà
B
proprietà commutativa
A+B =B+A
A
C
A
B
proprietà associativa
(A + B) + C = A + (B + C)
B
A
C
B
A
C
Scalare (k) per Vettore (A):
C = kA
A
A
C Y = kAY
♦ stessa direzione
♦ stesso verso se k>0
♦ verso opposto se k<0
C Z = kAZ
♦ modulo: C = k A
k=2:
vettore doppio
C X = kA X
(k 1 + k 2 )A = k 1 A + k 2 A
k ( A + B ) = kA + kB
Versore : vettore di modulo unitario
2
x
2
y
2
z
uˆ = u + u + u = 1
versori degli assi:
$x
ˆ = (1,0,0 ) = ˆi
!
!ˆ
ˆ
#y = ( 0,1,0 ) = j
!
!zˆ = ( 0,0,1) = kˆ
"
2A
−A
k = -1:
vettore opposto
Proprietà distributive.
Si può operare come con i numeri reali
modulo
A
A
direzione e verso uˆ A =
A
ˆA
A = Au
ˆ + Ay y
ˆ + Az zˆ
A = Ax x
Differenza di vettori.
C
A−B =C
A+ −B =C
A
-B
( )
B
-A è il vettore opposto di A
A
B
C
A−A=0
A+B =C⇒C−A = B
€ sui numeri reali.
si opera come
Anche qui vale la disuguaglianza triangolare:
a −b ≤ c ≤ a +b
Scomposizione di un vettore!
Scomposizione lungo due direzioni date.
Inversione della regola del parallelogramma:
y
r
c = a+b
a
c
b
aY
Ci interesserà solo la scomposizione lungo
direzioni ortogonali fra loro (assi cartesiani)
a
ĵ
r’
θ
aX
iˆ
x
aX e aY sono i vettori componenti di a
aX e aY sono le componenti (cartesiane) di a
a = ax + a y = axi + a y j
PN
PT
P
Esempio: scomposizione della forza peso su un piano inclinato.
Prodotto scalare!
Associa a 2 vettori uno scalare
A⋅B = c
A ⋅ B = AB cos θ
A ⋅ B = AX B X + AY BY + AZ BZ
Proprietà commutativa:
Proprietà distributiva:
θ
B
A⋅B = B⋅A
A ⋅ B + C = A ⋅B + A ⋅C
A ⋅ B = 0 ⇔ A e B ortogonali
A ⋅ B > 0 ⇔ 0 < θ < 90°
A ⋅ B < 0 ⇔ 90° < θ < 180°
Esempio: lavoro
A
(
)
2
A ⋅ A = A A cos 0 0 = A
xˆ ⋅ yˆ = xˆ ⋅ zˆ = yˆ ⋅ zˆ = 0
xˆ ⋅ xˆ = yˆ ⋅ yˆ = zˆ ⋅ zˆ = 1
ˆ = AX
A⋅x
uˆ ⋅ uˆ = 1
ecc.
minore dei due angoli
Prodotto vettoriale!
A×B = C
è un vettore (pseudovettore)
A × B = AB sin θ
θ = 0°
C
⇒C =0
B
θ = 180° ⇒ C = 0
θ = 90° ⇒ C = AB
Modulo: area del parallelogramma
Direzione: ortogonale ad A e B
Verso: mano destra o vite destrorsa
A
C
C
B
Proprietà anticommutativa:
A
B × A = −A × B
B
Proprietà distributiva:
A× B + C = A×B + A×C
(
)
Area del
parallelogramma
A
-C
B
A
Esempi di prodotto vettoriale in Fisica
http://it.wikipedia.org/wiki/File:Torque_animation.gif
Prodotto vettoriale!
componente di B
ortogonale ad A
A × B = AB sin θ
A × B X = AY B Z
A × B Y = AZ B X
A × B Z = AX BY
(
(
(
)
)
)
componente di A
ortogonale a B
Formalmente
= AB⊥ = A⊥ B
− AZ BY
− AX B Z
− AY B X
Proprietà anticommutativa:
B × A = −A × B
l’ordine dei fattori è importante
xˆ
Ax
Bx
yˆ
Ay
By
zˆ
Az
Bz
da cui
ˆ ×y
ˆ = zˆ
$x
!
!ˆ ˆ
ˆ
#y × z = x
!
ˆ =y
ˆ
!
"zˆ × x
permutazione
ciclica
Proprietà distributiva:
A× B + C = A×B + A×C
(
)
Derivata di un vettore:
Interpretazione geometrica.
dA
dA
=
dt
dA
C=
dt
dA X
dA
dA
xˆ + Y yˆ + Z zˆ
dt
dt
dt
Proprietà
A(t)
A(t+dt)
d
dA dB
A+ B =
+
dt
dt
dt
d
dk
dA
kA =
A+ k
dt
dt
dt
(
)
( )
Caso di vettore di modulo costante
d
dA
dB
A⋅B =
⋅ B + A⋅
dt
dt
dt
d
dA
dB
A× B =
× B + A×
dt
dt
dt
( )
( )
d
dA
A⋅A = 2
⋅A = 0 ⇒
dt
dt
(
)
dA
⊥A
dt
Ciò vale in particolare per i versori (ad es. versori degli assi).
ˆ
dx
ˆ
⊥x
dt
dxˆ
Esiste un vettore ω tale che:
= ω × xˆ
dt
ω ha il significato di velocità angolare: un vettore di modulo costante può solo ruotare.










