Statica
Equilibrio dei corpi
Corpo rigido
Momento di una forza
Condizione di equilbrio
Leve
Statica
La statica è la parte della meccanica che studia
l’equilibrio di un corpo materiale, ovvero le condizioni
necessarie affinché un corpo, inizialmente in quiete,
resti in quiete anche dopo l’intervento di forze esterne.
Nel corpo umano la conoscenza delle forze
agenti nei muscoli e nelle giunture è di grande
importanza per la medicina e la fisioterapia
Forza d’attrito
Risultante macroscopica delle azioni
tra molecole che si oppongono allo
scorrimento.
Quando proviamo a far scivolare un oggetto
su un altro microscopiche protuberanze si
oppongono al moto. Questo tipo di attrito
viene chiamato "attrito dinamico".
Quando un corpo è in moto lungo
una superficie rugosa, la forza di
attrito dinamico agisce in direzione
opposta alla velocità del corpo.
Fad = fd N
fd coeff. attrito
dinamico
Il modulo della forza di attrito dinamico
dipende dalla natura delle due superfici che
scivolano l’una sull’altra, ed è proporzionale
al modulo della forza normale al piano di
scorrimento.
Forza d’attrito
Esiste anche un attrito statico, forza
parallela alle due superfici, che è
presente in assenza di moto relativo.
Supponiamo di esercitare una
forza orizzontale su un banco,
ma questo non si muove
(la risultante delle forze è zero).
Deve quindi esistere una forza,
detta di attrito statico, che agisce sul
banco che gli impedisce di muoversi.
Fas = fs N
fs coeff. attrito
statico
Anche l’attrito statico è proporzionale
al modulo della forza normale
al piano di scorrimento.
Forza d’attrito
Si noti che è spesso più facile
mantenere un oggetto pesante
in movimento, rispetto a muoverlo
dalla sua posizione iniziale:
Fas ≥ Fad
Questo si traduce nella relazione:
fs ≥ fd
L’attrito fa venir meno la
conservazione dell’energia
meccanica, che invece degrada in
forme diverse di energia (calore).
Se si tiene conto di tutte le forme di
energia, questa si conserva!!!
Esempi
Lezione I 6 Momento di una forza
Il momento di una forza rispetto ad un punto O
ne misura la capacità di mettere in rotazione il
punto o oggetto a cui è applicata rispetto ad O.
Il momento di una forza
rispetto ad un punto è
definito come il prodotto
vettoriale tra il vettore
posizione e la forza:
M = r x F Momento di una forza
Il modulo di M è
r F sen α = F b
La grandezza r sen α,
distanza dell'asse di
rotazione dalla retta su
cui giace F, è detta
braccio della forza F.
Se F ed r sono perpendicolari, il braccio si identifica
con r, ed il momento è massimo.
M può essere nullo se F o b sono nulli, oppure
se F ed r sono paralleli.
Esempi
Coppia di forze: 2 forze uguali
in modulo e direzione ma verso
opposto, applicate in punti
diversi di un corpo rigido che
può ruotare attorno ad un asse.
Equilibrio di un corpo rigido
Un corpo rigido è per
definizione indeformabile.
Esso è in equilibrio se
le risultanti delle forze
e dei momenti sono
identicamente nulle:
Σ iF i = 0
ΣiMi = 0
• Le forze rendono conto
dei moti di traslazione
• I momenti dei moti di
rotazione.
Centro di massa o baricentro
Rappresenta il punto in cui si
può immaginare concentrata la
massa di un corpo esteso,
quando se ne vogliono
determinare le condizioni di
equilibrio o si vuole studiare il
suo comportamento dinamico.
xCM = (m1/M)r1+(m2/M)r2
M = m1+m2
Equilibrio nel corpo umano
Le condizioni di equilibrio sono identificate, in tre dimensioni, da tre
equazioni per l’equilibrio traslazionale e tre per l’eq. rotazionale:
! 1
2
N
F
+
F
+...
+
F
x
x =0
## x
" Fy1 + Fy2 +... + FyN = 0
# 1
2
N
F
+
F
+...
+
F
#$ z
z
z =0
Tuttavia, se si sceglie
opportunamente il piano punto
di applicazione delle forze O, si
possono approssimare tutte le
forze come giacenti sullo
stesso piano, e le 3 condizioni
rimanenti sono quelle per
le forze in x e y e per il
momento in z.
!
1
2
N
M
+
M
+...
+
M
x
x
x =0
##
" M 1y + M y2 +... + M yN = 0
#
1
2
N
M
+
M
+...
+
M
#$
z
z
z =0
Esempio: articolazione dell’anca
Equilibrio su un solo piede
Approx: forze giacenti nel piano verticale
passante per l’articolazione
• Fforza trazione glutei
• Pgforza peso gamba (~1/7 P corpo)
• Nreazione vincolare suolo = -P
• Rscarico peso corpo su articolazione = ?
Esempio: articolazione dell’anca
"
Rx = 0.55P
$$
Ry = 2.37 P
#
$
$% F = 1.61P → sost. 1 e 2 eq.
"$
R = 2.43P
#
θ
=
arccos
R
R
=
76.9
$%
x
• Equilibrio su un solo piede normale
durante deambulazione.
• Forza R circa due volte e mezzo P!
• Testa del femore cresce maggiormente
in direzione della forza R
(ossa crescono dove sollecitate).
Le leve
Una leva è una macchina semplice
che trasforma il movimento.
È composta da due bracci solidali fra loro (che
ruotano cioè dello stesso angolo e con la stessa
velocità angolare) incernierati per un'estremità ad
un fulcro, attorno al quale sono liberi di ruotare.
Condizione di equilibrio di una leva
La condizione di equilibrio di una leva è che la somma
dei momenti delle forze ad essa applicate sia nulla:
F1b1=F2b2
Da cui b1/b2=F2/F1 ovvero il braccio e la forza su di
esso applicata sono inversamente proporzionali.
La bilancia
Condizione di equilibrio di una leva
Perché sia garantito l’equilibrio, il braccio della forza
peso della palla di 5kg dev’essere 20 volte maggiore
di quello della forza peso della palla da 100kg.
Guadagno di una leva
Il rapporto tra forza resistente Fr e forza motore
(o potenza) Fp,
uguale al rapporto fra bp e br,
viene chiamato guadagno meccanico G.
G = Fr/Fp = bp/br
È una proprietà geometrica della leva!
Tipi di leve
Le leve si distinguono in:
• svantaggiose: se la forza applicata richiesta è maggiore della
forza resistente, ovvero se il braccio-resistenza è più lungo del
braccio-potenza
(bp / br < 1)
• indifferenti: se la forza applicata richiesta è uguale alla forza
resistente, ovvero se il braccio-resistenza è uguale al bracciopotenza
(bp / br = 1)
• vantaggiose: se la forza applicata richiesta è minore della
forza resistente, ovvero se il braccio-resistenza è più corto del
braccio-potenza
(bp / br > 1)
Esercizio
A che distanza deve mettersi la bambina (peso
minore) per bilanciare il peso del bambino.
Esercizio
Leve e conservazione energia meccanica
Leve e conservazione energia meccanica
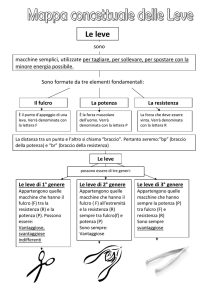
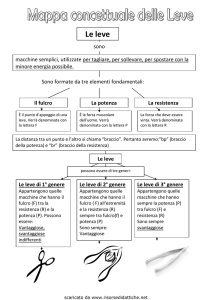
Tipi di leve
In base alla posizione reciproca del fulcro e
delle forze si ha un’ulteriore distinzione:
• I genere: il fulcro si trova tra
le due forze (vantaggiose,
svantaggiose o indifferenti)
• II genere: la forza resistente
si trova fra il fulcro e la forza
applicata (sempre vantaggiose)
• III genere: la forza applicata
si trova fra il fulcro e la forza
resistente (sempre svantaggiose)
Leve del corpo umano
Nel nostro corpo:
i muscoli scheletrici (elemento attivo) inserendosi
sulle ossa (elemento passivo) per mezzo della
contrazione muscolare determinano il movimento.
Questo è possibile grazie anche alle articolazioni,
le regioni di “snodo” tra le parti fisse.
Tutto l'apparato locomotore è basato su un
sistema di leve che possono essere di primo,
secondo o terzo tipo.
Leve del corpo umano
Nelle leve del corpo umano:
• Il fulcro è dato dall'asse di rotazione (di solito
l'articolazione, ma può anche essere un punto di
appoggio – piede – o di presa – mani);
• la potenza è data dal punto in cui viene applicata la
forza (di solito l'origine o l'inserzione muscolare);
• la resistenza è data dal punto in cui viene generata la
stessa forza resistente (un peso, la forza gravità della
parte del corpo interessata, ecc.).
Articolazione di appoggio della testa
Esempio di leva del I genere e svantaggiosa.
Per bilanciare il peso del capo ed evitare che la testa ciondoli in
avanti, viene esercitata una potenza da parte dei muscoli della nuca. L'intensità di Fm è tale da produrre un momento
uguale a quello prodotto da Fr:
Se il peso Fr della testa è di 8 Kg ~ 80N,
si avrebbe:
Fm = Fr 8/2 = 320 N (~ peso 32Kg)
8 cm 2 cm Si noti che l'insieme delle due forze tenderebbe
a causare un abbassamento del sistema: il
fulcro esercita anche una reazione vincolare che
si oppone alla traslazione. Per questo dopo un
certo tempo l'articolazione è affaticata.
Innalzamento sulle dita del piede
Esempio di leva del II genere
FT = Forza Motrice, forza
muscolare (polpaccio)
applicata dal tendine sul
calcagno.
FO = Forza Resistente, forza
esercitata dalle forze della
gamba (tibia e fibula) sul
piede.
10 cm
FP = reazione vincolare del
suolo sulla pianta del piede,
causata dalla forza peso del
corpo che agisce sul fulcro
(punto fermo).
Innalzamento sulle dita del piede
Equilibri traslazionali
• Verticale:
FT cos(7o) + FP = FO cos(θ)
• Orizzontale:
FT sin(7o)= FO sin(θ)
Equilibrio rotazionale rispetto al punto centrale:
5.6 * FT cos(7o) = 10 * FP
da cui si ricava
FT=10*FP/(5.6*0.992)=1.8*FP
Sostituendo nelle precedenti equazioni si ha:
10 cm
1.8* FP *0.992+ FP= FO cos(θ)
1.8* FP *0.122= FO sin(θ)
tg(θ)=0.2196/2.7856 FP= 0.079
da cui
θ=4.5ο, FO = 2.8 FP
Abduzione del braccio
Esempio di leva del III genere
In quale condizione è più faticoso tenere il libro?
Esempio di leva: l’apparecchio dentale
L’apparecchio dentale consiste in un filo metallico
sottoposto a una tensione di 2N. Esso quindi esercita
una forza di 2N sul dente nelle due direzioni come
indicato in figura. Calcolare la forza risultante sul
dente dovuta all’apparecchio
Esempio di leva: l’apparecchio dentale
Esempio: tensione nella corda del
lampadario
Esempio: tensione nella corda del
lampadario