Verifica 5 del 10 dicembre 2014 alcune soluzioni.

Alcune Soluzioni verifica 5.
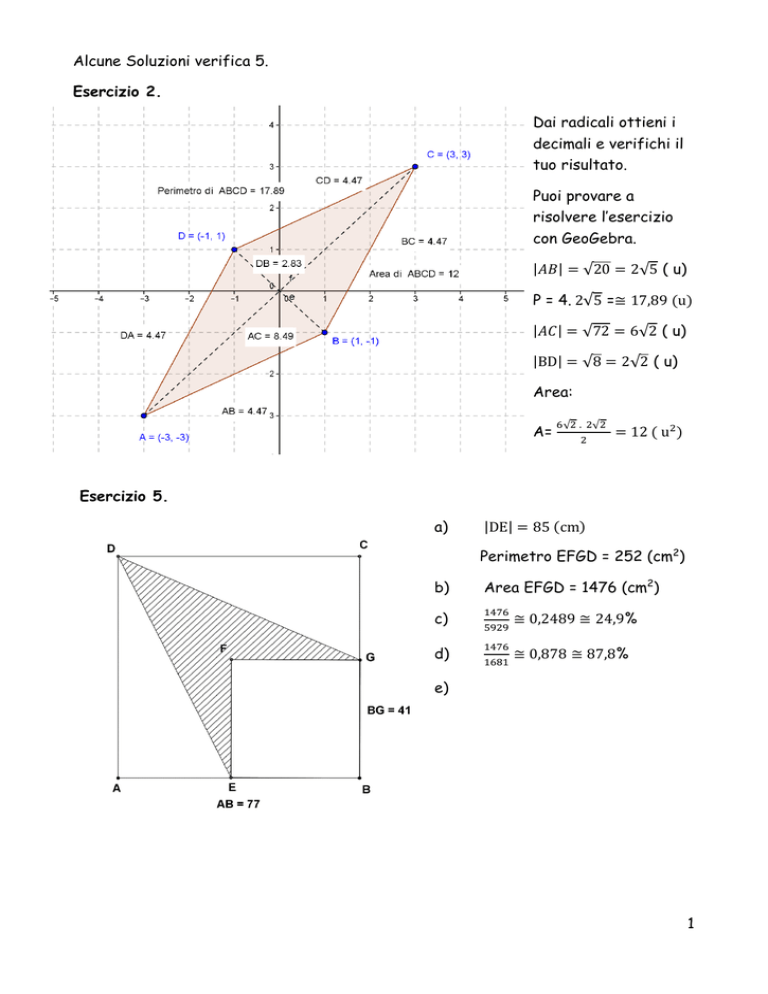
Esercizio 2.
Dai radicali ottieni i
decimali e verifichi il
tuo risultato.
Puoi provare a
risolvere l’esercizio
con GeoGebra.
|𝐴𝐵| = √20 = 2√5 ( u)
P = 4. 2√5 =≅ 17,89 (u)
|𝐴𝐶| = √72 = 6√2 ( u)
|BD| = √8 = 2√2 ( u)
Area:
A=
6√2 . 2√2
2
= 12 ( u2 )
Esercizio 5.
a)
|DE| = 85 (cm)
Perimetro EFGD = 252 (cm2)
b)
Area EFGD = 1476 (cm2)
c)
1476
d)
1476
5929
1681
≅ 0,2489 ≅ 24,9%
≅ 0,878 ≅ 87,8%
e)
1
Esercizio 6.
Attenzione il triangolo ABC è equilatero, dunque l’angolo ABC = 60° di conseguenza
l’angolo DBC = 120°.
Per il perimetro calcolare la misura dell’arco.
Perimetro figura:
16
3
π ≅ 16,76 ( cm)
Per l’area calcolare l’area del settore e quella del segmento circolare.
Area figura:
32
3
π − 8√3 ≅ 19,654 ( cm2 )
Esercizio 7.
|EG| = 6√2 (u)
1
|EI| = |EG|= 3√2 (u)
2
1
|EL| = |EB|= 3√2 (u)
2
Ma, |IL| devo calcolarlo nel seguente
modo:
|IL| = √32 + 32 = √18 = 3√2 ( u)
Dunque il triangolo è equilatero!
P = 3. 3√2 =𝟗√𝟐 (𝐮) ≅ 𝟏𝟐, 𝟕𝟑(𝐮)
Area del triangolo equilatero: A =
𝑙2 √3
4
2
=
(3√2) √3
4
=
𝟗√𝟑
𝟐
≅ 𝟕, 𝟕𝟗 (𝐮𝟐 )
2