Esercizio 4 (Greco): Esercitazione 3

Risoluzione esercizio 4
Esercitazione 3
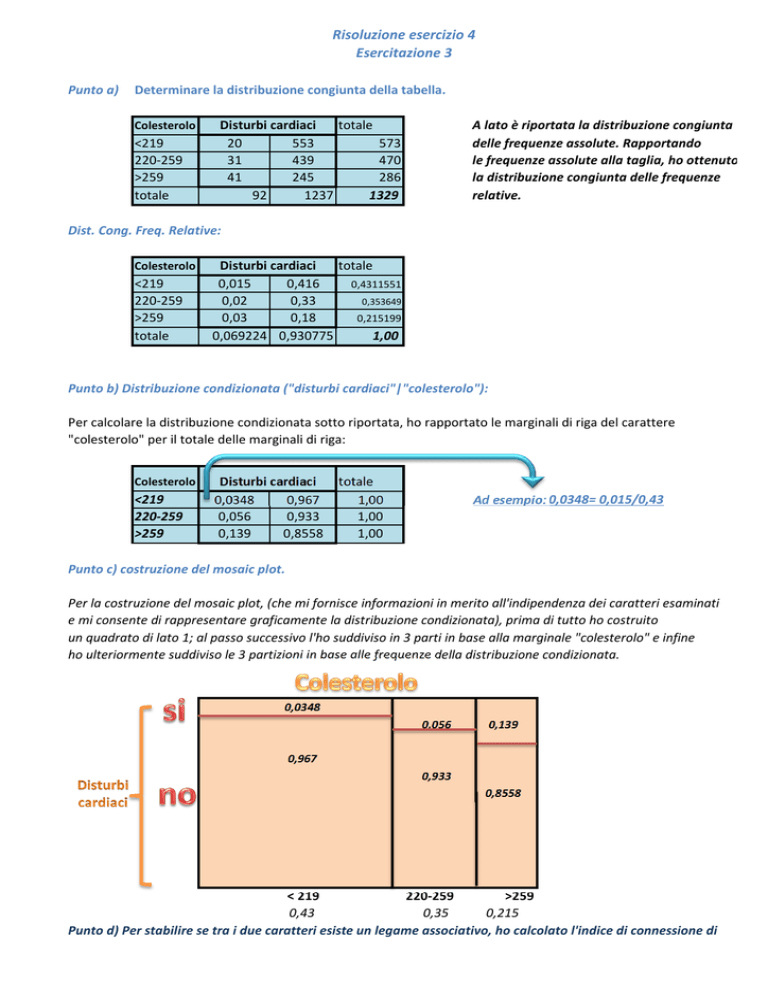
Punto a)
Determinare la distribuzione congiunta della tabella.
Colesterolo
<219
220-259
>259
totale
A lato è riportata la distribuzione congiunta
delle frequenze assolute. Rapportando
le frequenze assolute alla taglia, ho ottenuto
la distribuzione congiunta delle frequenze
relative.
Disturbi cardiaci
totale
20
553
573
31
439
470
41
245
286
92
1237
1329
Dist. Cong. Freq. Relative:
Colesterolo
<219
220-259
>259
totale
Disturbi cardiaci
totale
0,015
0,416
0,4311551
0,02
0,33
0,353649
0,03
0,18
0,215199
0,069224 0,930775
1,00
Punto b) Distribuzione condizionata ("disturbi cardiaci"|"colesterolo"):
Per calcolare la distribuzione condizionata sotto riportata, ho rapportato le marginali di riga del carattere
"colesterolo" per il totale delle marginali di riga:
Colesterolo
<219
220-259
>259
Disturbi cardiaci
0,0348
0,967
0,056
0,933
0,139
0,8558
totale
1,00
1,00
1,00
Ad esempio: 0,0348= 0,015/0,43
Punto c) costruzione del mosaic plot.
Per la costruzione del mosaic plot, (che mi fornisce informazioni in merito all'indipendenza dei caratteri esaminati
e mi consente di rappresentare graficamente la distribuzione condizionata), prima di tutto ho costruito
un quadrato di lato 1; al passo successivo l'ho suddiviso in 3 parti in base alla marginale "colesterolo" e infine
ho ulteriormente suddiviso le 3 partizioni in base alle frequenze della distribuzione condizionata.
0,0348
0,056
0,139
0,967
0,933
0,8558
< 219
220-259
>259
0,43
0,35
0,215
Punto d) Per stabilire se tra i due caratteri esiste un legame associativo, ho calcolato l'indice di connessione di
Risoluzione esercizio 4
Esercitazione 3
Cramer.
Distribuzione frequenze relative se indipendenti: verifico che le frequenze relative congiunte siano il prodotto
delle frequenze relative marginali, per riconoscere se le due variabili sono indipendenti.
Colesterolo
Disturbi cardiaci
totale
Colesterolo
<219
0,431151*0,06922 0,431151*0,9307
4=0,029845996 75= 0,401304572
0,43115
220-259
0,353649*0,06922 0,353649*0,9307
4=0,024480998 75 =0,329167648
0,35
220-259
0,215199*0,06922 0,215199*0,9307
4 =0,014896935 75=0,200301849
0,21
>259
>259
totale
≈0,069
<219
Disturbi cardiaci
0,029845996*
1329=39,67
533,33
32,535
437,46
19,8
266,2
≈0,93
I valori ottenuti nella tabella a sinistra, vanno
moltiplicati per la taglia (1329), al fine di ottenere le
frequenze assolute se indipendenti (nij)
Al passo successivo è necessario innanzitutto fare la differenza tra la tabella delle frequenze assolute e quella
delle frequenze assolute se indipendenti, al fine di poter studiare la connessione tra i due caratteri:
Distrib. Congiunta freq. Assolute
Colesterolo
Disturbi cardiaci
totale
Dist. Congiunta freq. Assolute se indipendenti
Colesterolo
Disturbi cardiaci
<219
220-259
>259
totale
573
470
286
1329
<219
220-259
>259
Colesterolo
Disturbi cardiaci
-19,67
19,67
-1,54
1,54
21,2
-21,2
20
31
41
92
553
439
245
1237
<219
220-259
>259
0,029845996*
1329=39,67
533,33
32,535
19,8
437,46
266,2
E' importante che
la somma dei
valori sulle righe e
sulle colonne
faccia zero
La tabella ottenuta deve essere normalizzata dividendo ciascun valore per le frequenze assolute se indipendenti
(ottenendo così:
Cij).
<219
-0,4958
0,03688
220-259
-0,047
0,0035
Ultimo passaggio prima di calcolare l'indice di
connessione è quello di elevare al quadrato e
moltiplicare per le frequenze assolute se indipendenti i
1,07
-0,0796
valori ottenuti. (Ottenendo così:
Colesterolo
>259
Disturbi cardiaci
Cij^2 * nij)
Risoluzione esercizio 4
Esercitazione 3
Colesterolo
<219
220-259
>259
Disturbi cardiaci
9,75
0,0718
22,669
0,7254
0,0053
1,6866
Cr*=√[∑∑c
ij
* nij]/[n*min(r-1,s-1)]
Dall'indice calcolato si evince
un moderato livello di
connessione tra i due caratteri.
Cr*=√(34,91/1329*1)=0,16
Punto e)
Per il calcolo delle probabilità richieste dalla traccia, ho costruito il diagramma ad albero:
0,43
"<219"
0,35
"220-259"
0,215
">259"
"DIST. SI"
0,0348
P("DIST SI"|"<219")
"DIST. NO"
0,967
P("DIST NO"|"<219")
"DIST. SI"
0,056
P("DIST SI"|"220-259")
"DIST NO"
0,933
P("DIST NO"|"220-259")
"DIST. SI"
"DIST. NO"
0,139
0,8558
P("DIST SI"|">259")
P("DIST NO"|">259")
Considerando normali valori del colesterolo compresi tra [220;259], ho calcolato la probabilità che scelto a caso
un paziente, questo abbia un valore del colesterolo non-normale:
P("<219"U">259")= P("<219")+P(">259")= 0,43+0,215= 0,645
Punto f) Probabilità che scelto a caso un soggetto, questo, sia sano; ossia non soffra di disturbi cardiaci né di
valori anomali del colesterolo.
P("DIST. NO" П "220-259") = P("DIST. NO"|"220-259")*P("220-259")= 0,933*0,35 = 0,32655
Punto g) Probabilità che un soggetto scelto a caso soffra di colesterolo alto e non soffra di disturbi cardiaci:
P("DIST. NO" П ">259") = P("DIST. NO"|">259")*P(">259")= 0,8558*0,215=0,1839
Punto h) Probabilità che un soggetto scelto a caso soffra di colesterolo alto se non soffre di disturbi cardiaci.
Risoluzione esercizio 4
Esercitazione 3
P(">259|"DIST. NO")=
P(">259"П "DIST.NO")
P("DIST.NO")
Al numeratore ho utilizzato la probabilità
dell'intersezione, mentre al denominatore
ho applicato il teorema delle alternative:
P(A|B)= ∑ P(A|Bi)*P(Bi).
Teorema delle alternative
"<219"
0,43
0,35
"220-259"
0,215
">259"
P("DIST. NO")= P("DIST.NO"|"<219")*P("<219")+P("DIST.NO"|"220-259")*P("220-259")+
P("DIST.NO"|">259")*P(">259")=
"DIST. SI"
"DIST. NO"
"DIST. SI"
"DIST NO"
"DIST. SI"
"DIST. NO"
0,0348
0,967
0,056
0,933
0,139
0,8558
P("DIST SI"|"<219")
P("DIST NO"|"<219")
P("DIST SI"|"220-259")
P("DIST NO"|"220-259")
P("DIST SI"|">259")
P("DIST NO"|">259")
P("DIST. NO")= (0,967*0,43)+(0,933*0,35)+(0,8558*0,215)= 0,93
In definitiva:
P(">259|"DIST. NO")=
0,1839
0,93
0,1978
Punto i) Probabilità che un soggetto non soffra di disturbi cardiaci se soffre di colesterolo alto.
P("DIST. NO"|">259")= [P("DIST. NO"П ">259")/P(">259")] = 0,1839/0,215 = 0,855
Punto j) Tra i livelli di colesterolo, qual è la causa più probabile di disturbi cardiaci?
Per rispondere a tale quesito, ho deciso di applicare il Teorema di Bayes secondo cui: individuato l'effetto "B", si
valuta la probabilità che la causa sia stata "A".
Secondo l'approccio bayesiano: P(A|B)=] P(B|A)*P(A)] / P(B)
0,43
0,35
0,215
"<219"
"220-259"
">259"
"DIST. SI"
"DIST. NO"
"DIST. SI"
"DIST NO"
"DIST. SI"
"DIST. NO"
0,0348
0,967
0,056
0,933
0,139
0,8558
P("DIST SI"|"<219")
P("DIST NO"|"<219")
P("DIST SI"|"220-259")
P("DIST NO"|"220-259")
P("DIST SI"|">259")
P("DIST NO"|">259")
Risoluzione esercizio 4
Esercitazione 3
Qual è la probabilità che la causa dei disturbi cardiaci sia il colesterolo "<219"?
P("DIST.SI"|"<219")*P("<219")
P("DIST.SI")
P("<219"|"DIST. SI")=
Teorema delle alternative
0,0348*0,43
(0,0348*0,43)+(0,056*0,35)+(0,139*0,215)
P("<219"|"DIST. SI")=
Nel 23% dei casi il
colesterolo basso, causa
disturbi cardiaci.
Qual è la probabilità che la causa dei disturbi cardiaci sia il colesterolo per valori compresi tra: 220 e 259?
P("<219"|"DIST. SI")=
P("220-259"|"DIST.SI")=
P("220-259"|"DIST.SI")=
0,23
P("DIST.SI"|"220-259")*P("220-259")
P("DIST.SI")
0,056*0,35
0,064449
P("220-259"|"DIST.SI")=
0,3
Nel 30% dei casi, il
colesterolo compreso tra
220 e 259, causa disturbi
cardiaci.
Qual è la probabilità che la causa dei disturbi cardiaci sia il colesterolo per valori superiori a 259?
P(">259"|"DIST.SI")=
P(">259"|"DIST.SI")=
Nel 46% dei casi
il colest. Alto
causa disturbi
cardiaci.
P("DIST.SI"|">259")*P(">259")
P("DIST.SI")
0,139*0,215
0,064449
P(">259"|"DIST.SI")=
0,46
In definitiva osservando le tre diverse probabilità ottenute possiamo dedurre che: è il colesterolo
alto, (ossia ">259"), la causa più probabile dei disturbi cardiaci.
ho ottenuto
Risoluzione esercizio 4
Esercitazione 3
Risoluzione esercizio 4
Esercitazione 3
Risoluzione esercizio 4
Esercitazione 3
Risoluzione esercizio 4
Esercitazione 3
Risoluzione esercizio 4
Esercitazione 3