sintesi

IL PIANO CARTESIANO
SCUOLA SECONDARIA 1^ GRADO
LUSIANA
IL PIANO CARTESIANO
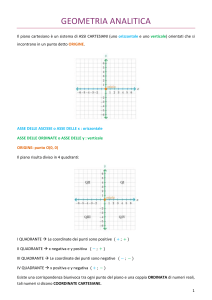
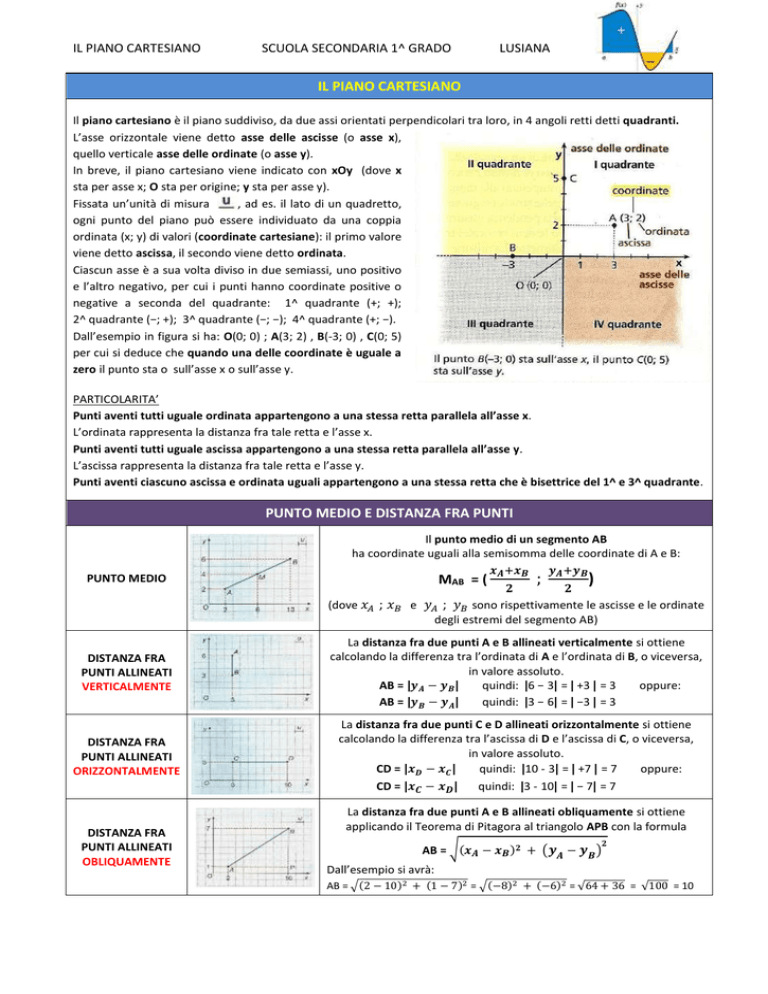
Il piano cartesiano è il piano suddiviso, da due assi orientati perpendicolari tra loro, in 4 angoli retti detti quadranti.
L’asse orizzontale viene detto asse delle ascisse (o asse x),
quello verticale asse delle ordinate (o asse y).
In breve, il piano cartesiano viene indicato con xOy (dove x
sta per asse x; O sta per origine; y sta per asse y).
Fissata un’unità di misura
, ad es. il lato di un quadretto,
ogni punto del piano può essere individuato da una coppia
ordinata (x; y) di valori (coordinate cartesiane): il primo valore
viene detto ascissa, il secondo viene detto ordinata.
Ciascun asse è a sua volta diviso in due semiassi, uno positivo
e l’altro negativo, per cui i punti hanno coordinate positive o
negative a seconda del quadrante: 1^ quadrante (+; +);
2^ quadrante (−; +); 3^ quadrante (−; −); 4^ quadrante (+; −).
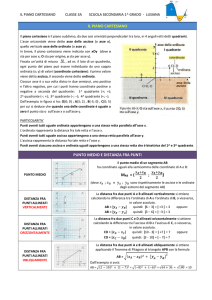
Dall’esempio in figura si ha: O(0; 0) ; A(3; 2) , B(-3; 0) , C(0; 5)
per cui si deduce che quando una delle coordinate è uguale a
zero il punto sta o sull’asse x o sull’asse y.
PARTICOLARITA’
Punti aventi tutti uguale ordinata appartengono a una stessa retta parallela all’asse x.
L’ordinata rappresenta la distanza fra tale retta e l’asse x.
Punti aventi tutti uguale ascissa appartengono a una stessa retta parallela all’asse y.
L’ascissa rappresenta la distanza fra tale retta e l’asse y.
Punti aventi ciascuno ascissa e ordinata uguali appartengono a una stessa retta che è bisettrice del 1^ e 3^ quadrante.
PUNTO MEDIO E DISTANZA FRA PUNTI
PUNTO MEDIO
DISTANZA FRA
PUNTI ALLINEATI
VERTICALMENTE
DISTANZA FRA
PUNTI ALLINEATI
ORIZZONTALMENTE
Il punto medio di un segmento AB
ha coordinate uguali alla semisomma delle coordinate di A e B:
𝒙𝑨 +𝒙𝑩
𝒚𝑨 +𝒚𝑩
MAB = (
)
La distanza fra due punti A e B allineati verticalmente si ottiene
calcolando la differenza tra l’ordinata di A e l’ordinata di B, o viceversa,
in valore assoluto.
AB = |𝒚𝑨 − 𝒚𝑩 |
quindi: |6 − 3| = | +3 | = 3
oppure:
AB = |𝒚𝑩 − 𝒚𝑨 |
quindi: |3 − 6| = | −3 | = 3
La distanza fra due punti C e D allineati orizzontalmente si ottiene
calcolando la differenza tra l’ascissa di D e l’ascissa di C, o viceversa,
in valore assoluto.
CD = |𝒙𝑫 − 𝒙𝑪 |
quindi: |10 - 3| = | +7 | = 7
oppure:
CD = |𝒙𝑪 − 𝒙𝑫 |
DISTANZA FRA
PUNTI ALLINEATI
OBLIQUAMENTE
;
𝟐
𝟐
(dove 𝑥𝐴 ; 𝑥𝐵 e 𝑦𝐴 ; 𝑦𝐵 sono rispettivamente le ascisse e le ordinate
degli estremi del segmento AB)
quindi: |3 - 10| = | − 7| = 7
La distanza fra due punti A e B allineati obliquamente si ottiene
applicando il Teorema di Pitagora al triangolo APB con la formula
𝟐
AB = √(𝒙𝑨 − 𝒙𝑩 )𝟐 + (𝒚𝑨 − 𝒚𝑩 )
Dall’esempio si avrà:
AB = √(2 − 10)2 + (1 − 7)2 = √(−8)2 + (−6)2 = √64 + 36 = √100 = 10
IL PIANO CARTESIANO
SCUOLA SECONDARIA 1^ GRADO
LUSIANA
STUDIO DI FIGURE NEL PIANO CARTESIANO
Per studio di figure nel piano cartesiano si intende
la costruzione, l’analisi e il confronto di figure geometriche regolari e irregolari.
Il perimetro di una figura nel piano cartesiano è facilmente calcolabile conoscendo
CALCOLO
le misure dei lati.
DEL PERIMETRO
La lunghezza dei lati può essere calcolata con le formule di determinazione della
distanza tra due punti.
L’area di una figura nel piano cartesiano è facilmente calcolabile conoscendo la
CALCOLO
misura degli elementi significativi della figura (lati, base, altezza, diagonali, ecc.),
DELL’AREA
in modo da applicare le formule della geometria piana e ricorrendo, se necessario,
alla scomposizione della figura in figure geometriche note e più semplici.
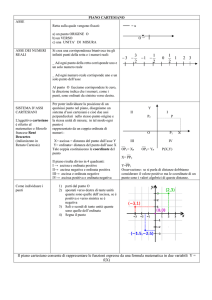
La formula di PICK si può applicare per il calcolo dell’area soltanto quando la
figura regolare o irregolare, convessa oppure concava, ha i vertici di coordinate
rappresentate da numeri interi; ad es.: A(-3; -8) ; B(+5; -12) ; C (-11; +23) ; ecc.
Per applicare tale formula è sufficiente:
1. contare i punti del piano interni alla figura (i);
2. contare i punti del contorno della figura (c);
3. sostituire i valori così trovati nella formula di PICK >>>
Esempi
Georg Alexander PICK
(1859-1942)
L’AREA CON LA
FORMULA DI PICK
A=i+½c–1
Triangolo rettangolo >>> i = 4 c = 9
A = 4 + ½ 9 – 1 = 7,5
Poligono irregolare >>> i = 9 c = 10
A = 9 + ½ 10 – 1 = 13
TRASFORMAZIONI NEL PIANO CARTESIANO
Sx
Sy
So
T
O
SIMMETRIA
RISPETTO
ALL’ASSE X
SIMMETRIA
RISPETTO
ALL’ASSE Y
SIMMETRIA
RISPETTO
ALL’ORIGINE
La figura F’ simmetrica della figura F rispetto all’asse x si
ottiene trasformando le coordinate dei vertici della figura F
secondo le seguenti due equazioni:
x’ = x
y’ = − y
La figura F’ simmetrica della figura F rispetto all’asse y si
ottiene trasformando le coordinate dei vertici della figura F
secondo le seguenti due equazioni:
x’ = − x
y’ = y
La figura F’ simmetrica della figura F rispetto all’origine O si
ottiene trasformando le coordinate dei vertici della figura F
secondo le seguenti due equazioni:
x’ = − x
y’ = − y
TRASLAZIONE
La figura F’ traslata a partire dalla figura F si ottiene
trasformando le coordinate dei vertici della figura F secondo
le seguenti due equazioni: x’ = x ± a y’ = y ± b ,
OMOTETIA
La traslazione può essere indicata anche dal vettore 𝐯⃗ (a; b)
La figura F’ omotetica della figura F si ottiene trasformando le
coordinate dei vertici della figura F secondo le seguenti due
equazioni:
x’ = k x
dove a e b sono i valori della traslazione rispettivamente secondo
l’ascissa e secondo l’ordinata.
y’ = k y
dove k > 0 oppure k < 0 è la caratteristica dell’omotetia.