Voltammetria idrodinamica
Il problema della variazione dello strato di
diffusione su elettrodi stazionari in
soluzione quiescente può essere risolto
agitando la soluzione.
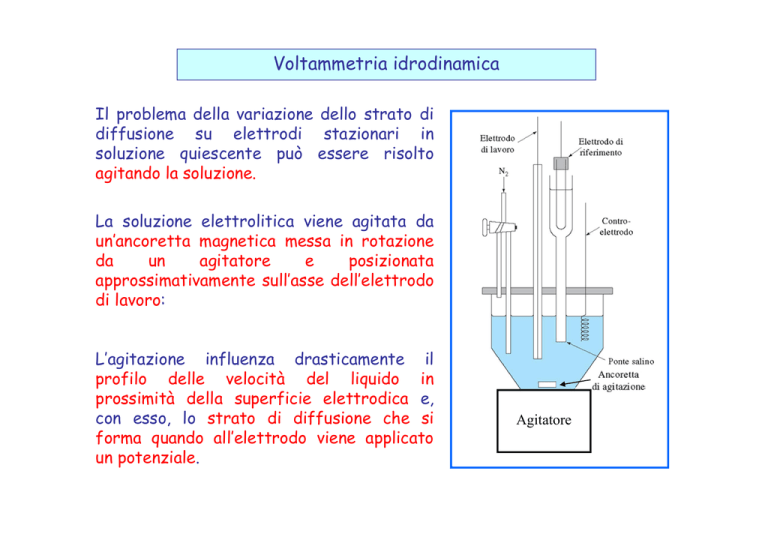
La soluzione elettrolitica viene agitata da
un’ancoretta magnetica messa in rotazione
da
un
agitatore
e
posizionata
approssimativamente sull’asse dell’elettrodo
di lavoro:
L’agitazione influenza drasticamente il
profilo delle velocità del liquido in
prossimità della superficie elettrodica e,
con esso, lo strato di diffusione che si
forma quando all’elettrodo viene applicato
un potenziale.
Agitatore
Profilo delle velocità del liquido
A grande distanza dalla superficie elettrodica il moto della soluzione è
turbolento, a causa della presenza dell’ancoretta rotante; avvicinandosi
alla superficie si incontra una regione a flusso laminare, regolare; in
stretta prossimità della superficie l’attrito con la superficie elettrodica
genera uno strato di soluzione stagnante.
Profilo delle concentrazioni all’interfaccia elettrodo-soluzione in soluzione
agitata
In pratica lo spessore dello strato di diffusione deriva dalla combinazione
di due fattori contrastanti:
1) l’incremento dovuto all’aumento del tempo;
2) la diminuzione
dall’agitazione.
dovuta
all’effetto
di
rimescolamento
creato
Di fatto si raggiunge una condizione stazionaria, in cui lo spessore dello
strato di diffusione è costante ed è tanto minore quanto maggiore è la
velocità di rotazione dell’ancoretta magnetica.
In tali condizioni si ha:
I = n F A q(x=0) = n F A D (C/x)x=0 = n F A D (Cbulk – Celet)/
con = strato di diffusione costante.
Effettuando una scansione lineare di potenziale è possibile dunque
registrare
l’onda
polarografica,
ottenendo
un
voltammogramma
idrodinamico. Il segnale sarà affetto soltanto da piccole fluttuazioni
(inferiori a quelle tipiche di un polarogramma), legate al riassestamento di
al variare del potenziale (e quindi di Celet).
Elettrodo a disco rotante (RDE)
Un approccio diverso alla voltammetria idrodinamica implica l’impiego di un
elettrodo a disco in grado di ruotare intorno al proprio asse, e quindi di
agitare la soluzione elettrolitica al posto dell’ancoretta magnetica.
Tale dispositivo viene definito elettrodo a disco rotante (Rotating Disk
Electrode, RDE):
L’elettrodo
di
lavoro
(RDE)
è
rappresentato da un disco di metallo (di
solito
Au,
Pt)
o
di
carbone
vetroso/grafite inglobato in un blocco
cilindrico in teflon che viene avvitato su
un asse rotante.
contatto
a spazzola
albero
motore
teflon
disco
elettrodico
L’albero
motore
è
collegato direttamente
al disco elettrodico e
il contatto elettrico
con l’esterno viene
realizzato
mediante
spazzole
metalliche
che strisciano sulla
superficie dell’albero
durante la rotazione.
Nel corso della rotazione il disco crea una
convezione forzata
nella
soluzione,
diretta perpendicolarmente ad esso a
distanza e tangenzialmente ad esso in
prossimità della superficie elettrodica.
L’analita viene dunque spinto verso la
superficie, dove avviene la reazione
redox.
Nell’ipotesi che il flusso di soluzione alla superficie elettrodica sia
laminare la variazione di concentrazione dell’analita nel tempo in
direzione normale alla superficie elettrodica è rappresentata da una
espressione diversa della seconda legge di Fick:
in cui x rappresenta la distanza dall’elettrodo e vx la velocità del liquido
spostato dalla convezione nella direzione x, mentre DC è il coefficiente di
diffusione dell’analita C.
L’equazione differenziale della diffusione all’RDE è stata risolta da
Levich attraverso un complesso trattamento matematico, portando
all’espressione dell’intensità di corrente in funzione del tempo.
A tale equazione si può arrivare, tuttavia, in modo alternativo,
considerando il profilo di diffusione dell’analita alla superficie
dell’elettrodo rotante e analizzando il profilo delle velocità del liquido
alla superficie in funzione della distanza dal centro del disco.
Il profilo delle velocità di un liquido che
lambisca una superficie solida immersa al
suo interno determina il cosiddetto
strato di Prandtl, *, uno spessore di
liquido in cui la velocità dei vari strati
aumenta man mano che ci si allontana
dalla superficie del solido fino a portarsi
al valore massimo, u0.
u0
*
u0
u0
u0
*
Y
*
In prossimità del punto d’impatto lo
strato di Prandtl non è costante, bensì
aumenta con la radice quadrata della
distanza y dal punto:
* = (y/u0)1/2
dove è la viscosità cinematica della
soluzione.
La viscosità cinematica di un liquido è data dal rapporto fra la viscosità
assoluta (misurata in Poise = g cm-1 s-1) e la densità (g cm-3) dunque le sue
unità sono quelle del coefficiente di diffusione, cm2s-1 (Stoke)
Il modello appena presentato può essere applicato al caso dell’RDE purché si
tenga conto di alcune differenze fondamentali.
In questo caso y = 0 rappresenta il punto centrale del disco e la coordinata y
aumenta simmetricamente a destra e sinistra, man mano che si procede
verso il bordo dell’elettrodo. La coordinata x rappresenta la direzione
perpendicolare all’elettrodo ed x aumenta allontanandosene.
Le linee di flusso del liquido risultano dalla combinazione di due vettori, uno
perpendicolare (vx) e l’altro parallelo alla superficie (uy): vx aumenta con x
fino al valore del bulk (v0), in modo indipendente da y; uy ha un profilo
parabolico ed il suo valore massimo [u0(y)] aumenta linearmente con y.
y=0
y=0
u0 (y1)
vx
x
x v0
uy
v0
y1
y2
u0(y2)
La soluzione delle equazioni della fluidodinamica dell’RDE mostra, infatti, che in
prossimità della superficie elettrodica y e u0(y) sono legate dalla seguente
relazione:
y/u0 (y) = 2.62 × -1
dove è la frequenza angolare di rotazione dell’elettrodo (in radianti/s).
Poiché:
* = (y/u0)1/2
l’aumento di y viene compensato
dall’aumento di u0, e ne deriva il
cosiddetto
paradosso
idrodinamico
dell’RDE, ossia il fatto che lo strato di
Prandtl sia costante lungo tutta la
superficie del disco rotante:
*
Y=0
La soluzione delle equazioni della diffusione all’RDE, ottenuta da Levich, mostra
che lo strato di diffusione è legato a * dalla relazione:
/* = (D/)1/3
Normalmente D e sono dell’ordine di 10-5 e 10-2 cm2/s, per cui corrisponde a
circa 1/10 di *, che, in soluzione acquosa, è dell’ordine di 10-2-10-3 cm.
Nel caso dell’RDE si può dunque ricavare:
= (D/)1/3 * =
= (D/)1/3 (y/u0)1/2 =
= D1/3 1/6 (y/u0)1/2
si ricava:
= 1.62 D1/3 1/6 -1/2
essendo
y/u0 (y) = 2.62 × -1
Riprendendo l’equazione per l’intensità di corrente ad un elettrodo piano in
condizioni di strato di diffusione stazionario:
I = n F A D (Cbulk – Celet)/
e sostituendo la nuova espressione per lo strato di diffusione si ottiene
l’Equazione di Koutecky-Levich per l’intensità di corrente all’elettrodo a
disco rotante:
I = n F A D (Cbulk – Celet)/ (1.62 D1/3 1/6 -1/2) =
= 0.62 nFAD2/3 1/2 -1/6 (Cbulk – Celet).
In condizioni di corrente limite, Celet = 0 e quindi:
Ilim = 0.62 nFAD2/3 1/2 -1/6 Cbulk
La dipendenza lineare dell’intensità di
corrente dalla radice quadrata della
velocità
angolare
di
rotazione
dell’elettrodo può essere confermata
sperimentalmente
registrando
voltammogrammi idrodinamici con l’RDE
rotante a velocità diverse e misurando
la corrente limite nei vari casi:
Si può così costruire il KouteckyLevich plot (Ilim vs 1/2), che
consente
di
risalire,
per
interpolazione lineare, alla pendenza
della retta e dunque a valori di
costanti come D e o alla stessa
superficie elettrodica A.
L’intervallo di valori accessibili per è limitato da due effetti:
a bassi valori, tipicamente inferiori a 10 Hz, lo strato di diffusione
diventa troppo grande, paragonabile al raggio del disco, e non valgono più le
condizioni del paradosso idrodinamico;
a valori alti di , dell’ordine di 105 Hz, il regime di flusso è turbolento
anche in prossimità della superficie elettrodica:
In realtà la transizione a flusso turbolento può essere facilitata dalla
presenza di asperità sulla superficie dell’elettrodo, inoltre alte velocità
provocano vortici in prossimità dell’elettrodo, pertanto non si opera mai a
frequenze di rotazione superiori a 1000 Hz.
Elettrodo a disco-anello rotante
(Rotating Ring-Disk Electrode, RRDE)
Rappresenta una variante dell’RDE molto utile per studiare gli intermedi di
processi elettrodici complessi o le cinetiche elettrochimiche.
Nella base dell’elettrodo sono
presenti un disco centrale e
un anello ad esso concentrico,
entrambi
in
materiale
conduttore, separati da un
anello isolante:
Il disco e l’anello lavorano
come elettrodi di lavoro
totalmente
indipendenti,
ciascuno ad un potenziale
controllato da uno specifico
circuito potenziostatico.
Contatto disco
Contatto anello
E’ possibile far avvenire all’elettrodo ad anello la reazione elettrodica
opposta a quella che avviene al disco, per verificare la stabilità del
prodotto di reazione redox prodotto su quest’ultimo.
Nel caso della riduzione di O2 ad H2O
è possibile avere conferma della
formazione dell’intermedio H2O2
applicando:
1) all’anello un potenziale costante
sufficiente a riossidare H2O2 a O2
(appena superiore a 0 V vs SCE)
2) al disco una scansione catodica
e seguendo la variazione della
corrente relativa al processo 1)
Se la specie che si forma sul disco è instabile e si trasforma in un’ulteriore
specie chimica non elettro-attiva, è possibile avere con l’RRDE una stima
della velocità di tale processo di trasformazione:
Supponendo che la reazione al disco
sia una riduzione:
asse di rotazione
anello
disco
anello
Ox + ne- Red
il prodotto di reazione Red tenderà a
diffondere verso il bulk della
soluzione e quindi verrà trasportato
dal flusso laminare verso l’anello.
Se nel corso di tale percorso subisce la reazione chimica:
Red In
con In = specie elettrochimicamente inerte
il numero di moli di Red che raggiungeranno l’anello e verranno riossidate a
Ox sarà tanto minore quanto più veloce è il processo di trasformazione di
Red, a parità di velocità di trasporto laminare (ossia di ).
Misurando la variazione dell’intensità di corrente all’anello con la velocità di
rotazione si può quindi avere una stima della velocità della reazione.