Analisi della fase di riscaldamento di un corpo solido
Si considera una lastra solida, omogenea di spessore “s”, riscaldata su una sola faccia.
Simboli:
T(x) è la temperatura in un punto generico distante “x*s” dal bordo non riscaldato della lastra (in
°C); è funzione del tempo “”.
T(c) è la temperatura nel bordo non riscaldato della lastra (per “x=0”) (in °C); è funzione del
tempo “”.
Tm
è la temperatura media del corpo all’istante considerato; è funzione del tempo “”.
Ta
è la temperatura media del corpo all’istante considerato; è funzione del tempo “”.
a
è un coefficiente di proporzionalità;
s
è lo spessore della lastra (in m)
è la conducibilità del materiale del corpo (in kcal/m*h*°C), ritenuto costante nel campo in
esame delle temperature;
cs
il calore specifico del materiale del corpo (in kcal/kg*°C), ritenuto costante nel campo in
esame delle temperature;
è la densità del materiale del corpo (in kg/m 3), ritenuto costante nel campo in esame delle
temperature;
A
è il coefficiente di scambio (in kcal/m2*h*°C) tra la superficie del corpo e l’ambiente esterno;
dipende dalle condizioni presenti e, di conseguenza, varia in funzione del tempo “”.
q
flusso termico trasmesso attraverso una superficie unitaria (in kcal/m 2).
Parametri:
x
parametro adimensionale; individua la posizione del punto nello spessore del corpo come
frazione dello spessore “s”; per la faccia non riscaldata x=0, per la faccia riscaldata: x=1.
rappresenta il tempo dall’istante di inizio del riscaldamento (in h).
Si ammette per ipotesi che il fenomeno sia costituito da una sequenza di stati di equilibrio, o
possano assimilarsi ad una sequenza di stati prossimi a quelli di equilibrio; questo significa che
l’effetto della conducibilità interna sia comparabile con quello dello scambio termico in superficie.
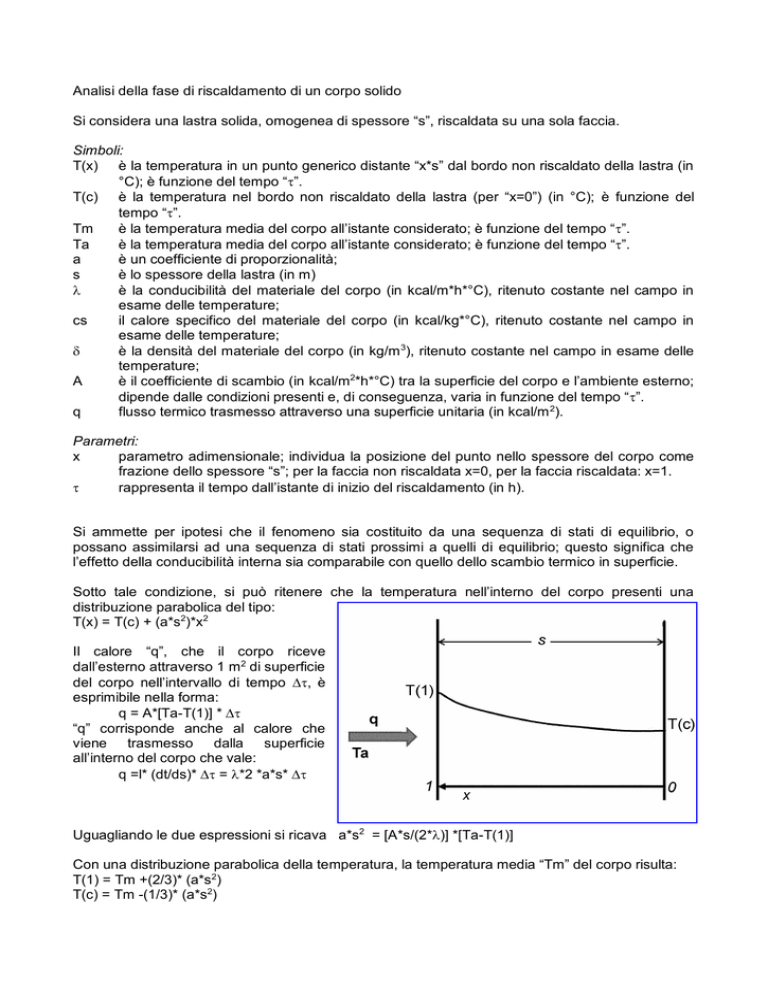
Sotto tale condizione, si può ritenere che la temperatura nell’interno del corpo presenti una
distribuzione parabolica del tipo:
T(x) = T(c) + (a*s2)*x2
Il calore “q”, che il corpo riceve
dall’esterno attraverso 1 m2 di superficie
del corpo nell’intervallo di tempo , è
esprimibile nella forma:
q = A*[Ta-T(1)] *
“q” corrisponde anche al calore che
viene trasmesso dalla superficie
all’interno del corpo che vale:
q =l* (dt/ds)* = *2 *a*s*
Uguagliando le due espressioni si ricava a*s2 = [A*s/(2*)] *[Ta-T(1)]
Con una distribuzione parabolica della temperatura, la temperatura media “Tm” del corpo risulta:
T(1) = Tm +(2/3)* (a*s2)
T(c) = Tm -(1/3)* (a*s2)
L’incremento “Tm” di temperature media del corpo dipende dalla quantità di calore che viene
fornita al corpo, e corrisponde a: Tm = [A*s/(cs**s)] *[Ta-T(1)] *
Queste relazioni permettono di effettuare una integrazione per intervalli finiti di tempo ”“.
Noti, in un certo istante generico, i valori delle variabili indicate è possibile calcolare l’incremento
“Tm” di temperatura del corpo e calcolare la temperatura media nell’istante successivo. Da
questo valore è possibile determinare i valori della temperatura della superficie riscaldata T(1) e
quella della superficie opposta T(c).
Questo procedimento non può essere ritenuto attendibile nella prima fase di riscaldamento,
quando l’ipotesi assunta non è verificata. Il calore che viene ricevuto dall’esterno non si diffonde
immediatamente all’interno dello spessore e la distribuzione di temperatura non può essere
ritenuta di forma parabolica.