Esame Scritto di Fisica 1 per Biotecnologie - 25 Febbraio 2010
Il tempo a disposizione è di tre ore. E’ ammesso l’uso di calcolatrici. Non è ammesso l’uso di appunti, libri, computer,
telefoni, altri dispositivi di comunicazione. Un libro di testo è a disposizione per consultazione. Costanti utili:
accelerazione di gravità g = 9.81 m/s2 ; massa dell’elettrone me = 9.10×10−31 kg; carica dell’elettrone e = 1.602×10−19
C; permeabilità dielettrica del vuoto 0 = 8.85 × 10−12 C2 /(Nm2 ). Si raccomanda di spiegare in modo conciso ma
chiaro il procedimento seguito. Ogni domanda sarà valutata fino a 4 punti.
Problema 1
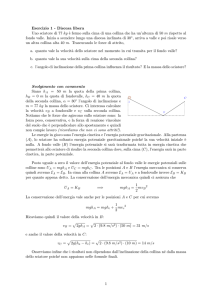
Uno sciatore di massa M = 70 kg si lancia partendo da fermo giù per un pendio di lunghezza d = 100m e angolo di
inclinazione costante θ rispetto al piano dell’orizzonte. Assumiamo che il coefficiente di attrito statico fra sci e neve
sia µs = 0.1 e che il coefficiente di attrito dinamico sia lo stesso. Si trascuri la resistenza dell’aria.
1. Qual è l’angolo θm di pendenza minima necessaria perchè lo sciatore possa iniziare a scivolare?
2. Assumendo θ = 2θm , qual è il tempo necessario perchè lo sciatore raggiunga la base del pendio?
3. Che velocità avrà raggiunto in quell’istante?
4. Quanto vale il lavoro fatto dalle forze di attrito?
Problema 2
Consideriamo un dipolo formato da un protone e un elettrone a distanza d = 2.0 × 10−10 m ed il piano ortogonale alla
retta congiungente le due cariche, passante per centro del dipolo O (il punto della retta equidistante dalle due cariche).
1. Calcolare il campo elettrico nel punto O e in un punto P del piano a distanza y = 1.0 × 10−10 m dal punto O
(perchè non serve specificare l’angolo?)
2. Supponiamo che il potenziale elettrico sul piano valga 0 per y → ∞. Quanto vale il potenziale elettrico nel punto
O? perchè?
Problema 3
Un elettrone penetra con velocità v = 4.5 × 105 m/s, diretta lungo l’asse x, in una zona di spazio (x > 0) dove è
presente un campo magnetico uniforme B = 0.12T, diretto lungo z.
1. Che traiettoria percorre l’elettrone nella zona dove è presente il campo magnetico?
2. A che distanza dal punto di ingresso l’elettrone esce dalla zona in cui il campo magnetico è presente, e in che
direzione viaggia?
3. Che energia cinetica ha l’elettrone quando esce dalla zona dove il campo magnetico è presente?
1
Esame Scritto di Fisica 1 per Biotecnologie - 25 Febbraio 2010 - Soluzioni
Problema 1
Scomponiamo la forza di gravità agente sullo sciatore in componente lungo il piano: f1 = M g sin θ, e normale al piano,
f2 = M g cos θ. La reazione vincolare del piano è uguale a −f2 (a meno che lo sciatore non stia sprofondando nella
neve!) normale al piano; la forza di attrito è dunque fµ ≤ µs f2 per sciatore fermo, fµ = µd f2 per sciatore in moto.
1. Lo sciatore è fermo se f1 = fµ , cioè sin θ ≤ µs cos θ. Da qui la “solita” condizione tan θm = µs , cioè θm = 5.71o .
2. Ora θ = 11.42o gradi. Lo sciatore percorre un tratto d con velocità iniziale nulla e accelerazione uniforme
a =p
g(sin θ − µd cos θ) = 0.1g, cioè a = 0.981m/s2 . Dall’equazione del moto: d = at2 /2 si ricava immediatamente
t = 2d/a = 14.3s.
3. Velocità finale: v = at = 14.0m/s.
4. Il lavoro fatto dalle forze di attrito (sempre negativo) è uguale alla differenza di energia meccanica (potenziale
2
3
+ cinetica) fra arrivo
R e partenza: Lµ = M v /2 − M gd sin θ = −6.73 × 10 J. E’ immediato verificare che questo
numero è uguale a f µ · dr = −µd M g cos θd.
Problema 2
Il campo elettrico è la somma vettoriale dei campi elettrici E+ e E− generati dalle due cariche. Prendiamo l’asse x
lungo l’asse del dipolo, l’origine delle coordinate nel centro O del dipolo, la carica positiva in −dx̂, quella negativa in
dx̂.
1. Nel punto O:
E+ =
con
E=
e
x̂ = E−
4π0 d2
−→
E = E x̂
e
1.602 × 10−19 C
=
= 2.88 × 1011 N C −1 .
2π0 d2
2 · 3.1415926 · 8.85 × 10−12 C 2 N −1 m−2 · 10−20 m2
Prendiamo il punto P sull’asse delle y, che prendiamo per comodità verticale. Nel punto P quindi:
E+ = Ex x̂ + Ey ŷ,
Ex =
e
cos θ,
4π0 r2
Ey =
e
sin θ,
4π0 r2
dove r2 = d2 + y 2 e θ è l’angolo fra l’asse del dipolo e la congiungente fra la carica positiva e il punto P : vale
cos θ = d/r. Analogamente si vede che E− = Ex x̂ − Ey ŷ da cui E = E x̂ con E = 2Ex . Questo risultato vale per
per tutti i punti su di una circonferenza di raggio y = d con centro in O, per via della simmetria del sistema di
cariche (una rotazione attorno all’asse del dipolo lascia il sistema immutato). Se y = d:
E = 2Ex =
e cos θ
1.602 × 10−19 C · 0.707
=
= 1.02 × 10−11 N C −1 .
2π0 r2
2 · 3.1415926 · 8.85 × 10−12 C 2 N −1 m−2 · 2 × 10−20 m2
2. Il calcolo precedente mostra che il campo elettrico su tutti i punti del piano è ortogonale al piano, quindi il
lavoro fatto dal campo per portare una carica di prova dall’infinito in O è nullo. In altre parole, il piano è
equipotenziale: il potenziale in O ha lo stesso valore che in un qualunque altro punto del piano, quindi VO = 0.
Problema 3
Assumiamo il campo B diretto lungo z. Sull’elettrone si esercita la forza di Lorentz, che è diretta lungo y: F = evB ŷ
(ricordarsi che x̂ × ẑ = −ŷ e che la carica dell’elettrone è negativa).
1. La forza di Lorentz è una forza centripeta che causa un moto circolare di raggio r, determinato dalla relazione
mv 2 /r = evB, e quindi
r=
9.1 × 10−31 kg · 4.5 × 105 m/s
mv
=
= 2.13 × 10−5 m.
eB
1.6 × 10−19 C · 0.12T
2
2. Dopo aver compiuto mezzo giro, l’elettrone torna nella zona priva di campo magnetico. Questo accade a distanza
d = 2r = 4.26 × 10−5 m = 42.6 micron dal punto di entrata. L’elettrone procede con velocità v lungo x, nella
direzione negativa.
3. Il campo magnetico non fa lavoro sulla particella, per cui la sua energia cinetica rimane invariata lungo tutta la
traiettoria:
mv 2
= 0.5 · 9.1 × 10−31 kg · (4.5 × 105 m/s)2 = 9.2 × 10−20 J.
E=
2
3