PROBLEMI DI FEM CINETICA 3
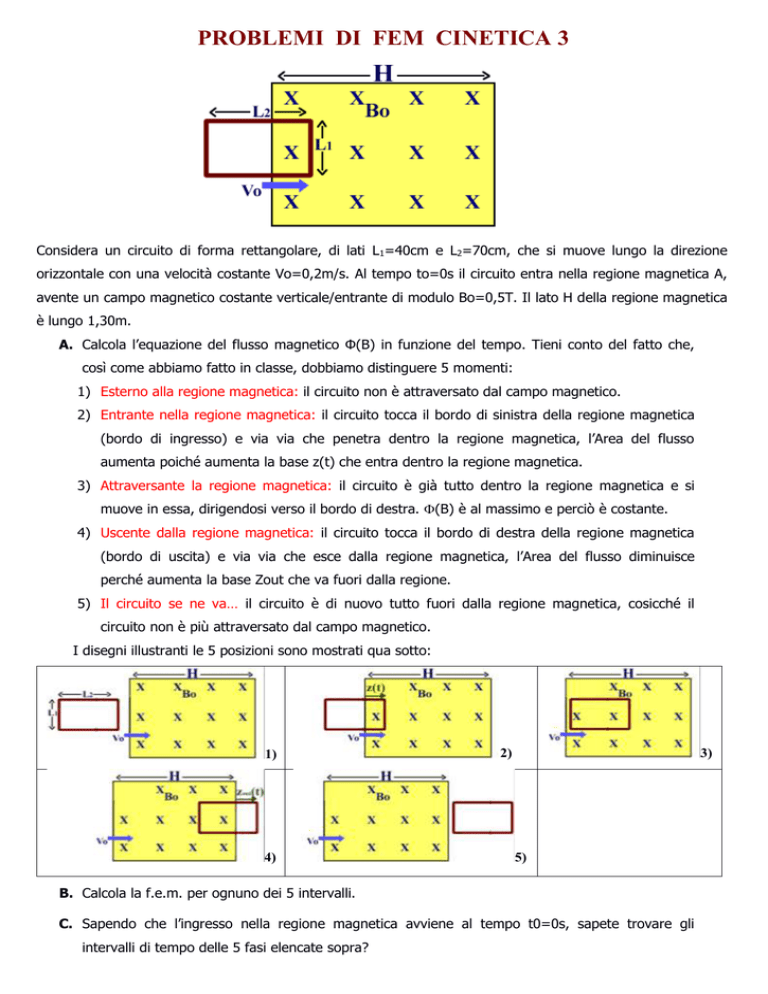
Considera un circuito di forma rettangolare, di lati L1=40cm e L2=70cm, che si muove lungo la direzione
orizzontale con una velocità costante Vo=0,2m/s. Al tempo to=0s il circuito entra nella regione magnetica A,
avente un campo magnetico costante verticale/entrante di modulo Bo=0,5T. Il lato H della regione magnetica
è lungo 1,30m.
A. Calcola l’equazione del flusso magnetico Φ(B) in funzione del tempo. Tieni conto del fatto che,
così come abbiamo fatto in classe, dobbiamo distinguere 5 momenti:
1) Esterno alla regione magnetica: il circuito non è attraversato dal campo magnetico.
2) Entrante nella regione magnetica: il circuito tocca il bordo di sinistra della regione magnetica
(bordo di ingresso) e via via che penetra dentro la regione magnetica, l’Area del flusso
aumenta poiché aumenta la base z(t) che entra dentro la regione magnetica.
3) Attraversante la regione magnetica: il circuito è già tutto dentro la regione magnetica e si
muove in essa, dirigendosi verso il bordo di destra. (B) è al massimo e perciò è costante.
4) Uscente dalla regione magnetica: il circuito tocca il bordo di destra della regione magnetica
(bordo di uscita) e via via che esce dalla regione magnetica, l’Area del flusso diminuisce
perché aumenta la base Zout che va fuori dalla regione.
5) Il circuito se ne va… il circuito è di nuovo tutto fuori dalla regione magnetica, cosicché il
circuito non è più attraversato dal campo magnetico.
I disegni illustranti le 5 posizioni sono mostrati qua sotto:
1)
4)
2)
3)
5)
B. Calcola la f.e.m. per ognuno dei 5 intervalli.
C. Sapendo che l’ingresso nella regione magnetica avviene al tempo t0=0s, sapete trovare gli
intervalli di tempo delle 5 fasi elencate sopra?
SOLUZIONI:
A. Per il calcolo di (B):
1) Esterno alla regione magnetica: (B)=0
2) Entrante nella regione magnetica:(B) = BoArea = BoL1Z(t) ; la base Z è indicata
come Z(t) in quanto essa cambia al passare del tempo: infatti: Z(t) = Vo(t-to) = (to=0s)
= Vot (B) = BoL1Vot
3) Attraversante la regione magnetica: (B) = BoArea e poiché il circuito è già tutto dentro
la regione magnetica, Area = L1L2 (B)=BoL1L2.
4) Uscente dalla regione magnetica: (B) = BoArea; poiché il circuito esce di un tratto Zout
(ho chiamato questo tratto Zout per distinguerlo da Z, che era il tratto quando il circuito
entrava dentro la regione magnetica), la base dentro la regione magnetica è (L2-Zout)
Area = L1(L2-Zout) (B) = BoL1[L2-Zout(t)]. E’ evidente che Zout = Vo(t-tout),
con tout il tempo di inizio dell’uscita del circuito (ho scritto tout per non confonderlo con to, il
tempo di ingresso nel circuito). Se ci pensate un attimo, tenendo conto della lunghezza del
tratto H, della lunghezza del lato L2 e della velocità Vo, risulta che tout=6,5s: ma per adesso
continuiamo a chiamare questo valore tout senza preoccuparci del suo valore:
(B)=BoL1[L2-Vo(t-tout)].
5) Il circuito se ne va… adesso esso è di nuovo tutto fuori dalla regione magnetica, cosicché il
flusso è sempre nullo: (B)=0.
B. Per il calcolo della f.e.m. è sufficiente applicare l’eq. = -D(B)/Dt = -̇ . Fate la derivata e
poi cambiate il segno. E fatela bene, sennò chiamo la Prof di matematica! Risulta subito:
1) =0 Volt ; 2) =-BoL1Vo ; 3) =0 Volt ; 4) =+BoL1Vo ; 5) =0 Volt
C. 1) Poiché è detto che il circuito tocca la regione magnetica per t=0s, esso è esterno ad essa
per t< 0s ; 2) Al tempo t=0s inizia ad entrare nella regione magnetica: l’ingresso finisce
quando tutto il lato L2 è penetrato dentro: è immediato calcolare che questo avviene dopo
3,5s e perciò: 0s<t<3,5s ; 3) L’attraversamento della regione magnetica inizia da
quando il lato L2 è tutto entrato dentro fino a quando il circuito tocca il lato esterno destro
della regione magnetica ed inizia ad uscire. E’ immediato capire che l’attraversamento
impiega uno spazio di H-L2=60cm alla velocità Vo=20cm/s e perciò esso dura 3s. Ne segue
che:
3,5s<t<6,5s
;
4) L’uscita dalla regione magnetica dura fintantoché il lato L 2
attraversa il confine: poiché L2=70cm e la velocità è Vo=20cm/s, esso dura 3,5s. Dunque:
6,5s<t<10s ; 5) A questo punto, è immediato capire che il circuito se ne va per t>10s]
INOLTRE RISOLVI QUESTI ALTRI PROBLEMI:
Disegna sul grafico A il flusso (B) rispetto al tempo (hint: il grafico sarà formato da una
spezzata: retta inclinata verso l’alto/retta orizzontale/retta inclinata verso il basso).
Disegna sul grafico B la fem indotta rispetto al tempo (hint: sarà una linea discontinua…).
Supponi che la resistenza del circuito sia R=10 Ohm: calcola la corrente indotta Io
[R:
Nei punti 1), 3), 5): Io=0 A . Nei punti 2) , 4) : Io=0,004 A (in val. assoluto)]
Calcola la forza magnetica (Fm) generata sul circuito [R: Fm=0,0008N]
(Questi ultimi problemi non li abbiamo ancora fatti: teneteli “al caldo” per la lezione in classe)
Calcola la potenza che Fm produce; [Potenza=0,00016 Watt]
Verifica che questa potenza è uguale a quella elettrica.
Commenta questa frase: “L’uguaglianza -in modulo- fra la potenza di Fm e quella elettrica è
una conseguenza della Legge di Conservazione dell’Energia e dimostra che l’induzione
magnetica trasduce l’energia.”












