A
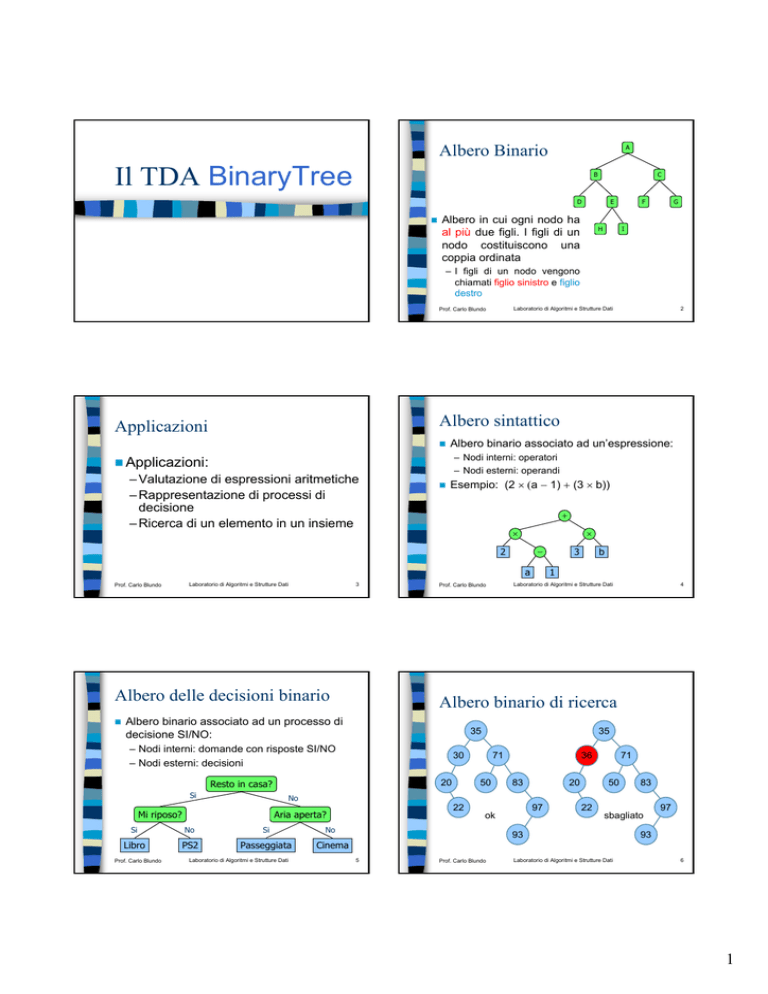
Albero Binario
Il TDA BinaryTree
B
C
D
E
Albero in cui ogni nodo ha
al più due figli. I figli di un
nodo costituiscono una
coppia ordinata
H
F
G
I
– I figli di un nodo vengono
chiamati figlio sinistro e figlio
destro
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
Albero sintattico
Applicazioni
Albero binario associato ad un’espressione:
– Nodi interni: operatori
– Nodi esterni: operandi
Applicazioni:
– Valutazione di espressioni aritmetiche
– Rappresentazione di processi di
decisione
– Ricerca di un elemento in un insieme
Esempio: (2 × (a − 1) + (3 × b))
+
×
×
−
2
a
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
3
Albero delle decisioni binario
b
1
4
Albero binario di ricerca
35
– Nodi interni: domande con risposte SI/NO
– Nodi esterni: decisioni
35
30
Resto in casa?
20
Si
3
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
Albero binario associato ad un processo di
decisione SI/NO:
71
50
36
83
20
71
50
83
No
Mi riposo?
22
Aria aperta?
Si
No
Si
No
Libro
PS2
Passeggiata
Cinema
Prof. Carlo Blundo
2
Laboratorio di Algoritmi e Strutture Dati
97
ok
22
sbagliato
93
5
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
97
93
6
1
Interfaccia BinaryTree
Il TDA BinaryTree
Il TDA BinaryTree è una specializzazione di
Tree che supporta tre metodi addizionali
leftChild(v)
– Restituisce il figlio sinistro di v oppure errore se v
non ha un figlio sinistro
rightChild(v)
– Restituisce il figlio destro di v oppure errore se v
non ha un figlio destro
sibling(v)
– Restituisce il fratello di v oppure errore se v non
ha un fratello
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
7
Gerarchia completa
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
8
Struttura dati per rappresentare BinaryTree
InspectableContainer
size – isEmpty – elements
Possiamo
rappresentare il TDA Position
tramite un nodo che contiene
InspectablePositionalContainer
positions
InspectableTree
PositionalContainer
root – parent – children isIntenal
– isExternal – isRoot
public interface InspectableBinaryTree
extends InspectableTree {
// Metodi di accesso
/** restituisce il figlio sinistro di un nodo */
public Position leftChild(Position v);
/** restituisce il figlio destro di un nodo */
public Position rightChild(Position v);
/** restituisce il fratello di un nodo */
public Position sibling(Position v);
}
public interface BinaryTree
extends InspectableBinaryTree, PositionalContainer { }
replaceElement – swapElement
InspectableBinaryTree
Tree
leftChild – rightChild – sibling
– un riferimento ad un elemento
– un riferimento al nodo genitore
– un riferimento al figlio sinistro
– un riferimento al figlio destro
Graficamente ….
BinaryTree
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
9
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
10
Classe BTNode – 1
∅
public class BTNode implements Position {
B
∅
B
A
A
D
∅
∅
∅
E
C
Prof. Carlo Blundo
public BTNode() {}
D
∅
C
private Object element;
private BTNode left, right, parent;
∅
Laboratorio di Algoritmi e Strutture Dati
E
11
public BTNode(Object o, BTNode u,
BTNode v, BTNode w) {
setElement(o); setParent(u);
setLeft(v); setRight(w);
}
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
12
2
Classe BTNode – 2
Un’altra rappresentazione
public Object element() { return element; }
public void setElement(Object o) { element = o; }
public BTNode getLeft() { return left; }
public void setLeft(BTNode v) { left = v; }
• p(v)=1
public BTNode getRight() { return right; }
– se v è il figlio sinistro di u allora
public void setRight(BTNode v) { right = v; }
• p(v)=2p(u)
– se v è il figlio destro di u allora
public BTNode getParent() { return parent; }
• p(v)=2p(u)+1
public void setParent(BTNode v) { parent = v; }
}
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
13
Esempio
1 B
2 A
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
14
Implementazione
statica: è necessaria
una stima del numero massimo di nodi
dell’albero
3 D
4
D
5
C
In A[0] potremmo memorizzare il numero di
elementi nell’albero binario
Problemi con gli array
B
A
Si usa un array A
Ogni nodo v è memorizzato in posizione p(v)
– se v è la radice allora
E
– può portare a spreco di risorse
– nel caso peggiore, un albero con n nodi
richiede un vettore con 2n-1 elementi (se
l’albero degenera in una catena)
6 C
7 E
• Provarlo come esercizio
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
15
Esercizi
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
16
Esercizi
Implementare l’interfaccia BinaryTree
(scrivere il codice della classe
LinkedBinaryTree) usando
l’implementazione BTNode per Position
Scrivere il codice della classe
ArrayBinaryTree che implementa
l’interfaccia BinaryTree utilizzando un array
per memorizzare i nodi dell’albero
Testare
le classi LinkedBinaryTree e
ArrayBinaryTree provando tutti i metodi
Valutare
le differenze della complessità
computazionale dei metodi implementati
nelle due classi
– In questo caso come possiamo implementare
Position?
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
17
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
18
3
Visita postorder
Visita preorder
Le visite in alberi attraversano
tutti i nodi dell’albero in
Algorithm preOrder(v)
maniera sistematica
visit(v)
Preorder:
un
nodo
è
ispezionato prima dei suoi
for each child w of v
discendenti
preOrder (w)
Applicazioni:
stampa
dell’indice di un documento
strutturato
1 Data Structures and Algorithms in Java
Un nodo è ispezionato dopo
i suoi discendenti
Applicazione:
calcola
lo
spazio usato dai file in
directory e sotto-directory
9
LASD/
3
2
5 2. OOP
4
1.2 Methods
1.8 Packages
9 Bibliography
7
6
3
2.1 Exception
8
2.7 Exercises
2.5 Casting
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
2
listaE.doc
200K
1
6
Stack.ppt
64.5K
6
Queue.ppt
96.5K
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
7
4
5
Intro.ppt
85.5K
20
Visita inorder in alberi binari
1
5
4
1
Ulteriori esempi
3
studenti.xsl
53K
Slide/
primaProva.doc
27.5K
19
8
7
ESAMI/
1. Java Programming
2
Algorithm postOrder(v)
for each child w of v
postOrder (w)
visit(v)
3
6
7
2
preorder
4
5
Un nodo è ispezionato dopo il suo sottoalbero sinistro e prima del suo sotto-albero
destro
Applicazione: disegnare un albero binario
– x(v) = # nodi sotto-albero sinistro di v
• rango inorder (numero di elementi visitati prima di v
durante la visita inorder)
postorder
– y(v) = profondità di v
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
21
Algorithm inOrder(v)
if isInternal (v)
inOrder (leftChild (v))
visit(v)
if isInternal (v)
inOrder (rightChild (v))
6
Specializzazione della visita
postorder
– chiamate ricorsive
calcolano i valori dei
sotto-alberi
– visitando un nodo,
combina i risultati ottenuti
dai sotto-alberi
+
8
4
1
3
Prof. Carlo Blundo
7
×
9
5
23
Prof. Carlo Blundo
Algorithm evalExpr(v)
if isExternal (v)
return v.element ()
else
x ← evalExpr(leftChild (v))
y ← evalExpr(rightChild (v))
⊗ ← operator stored at v
return x ⊗ y
×
−
2
5
Laboratorio di Algoritmi e Strutture Dati
22
Valutazione espressioni aritmetiche
Algoritmo ed esempio
2
Laboratorio di Algoritmi e Strutture Dati
Prof. Carlo Blundo
3
2
1
Laboratorio di Algoritmi e Strutture Dati
24
4
Esercizi
Suggerimenti
Aggiungere, alla classe LinkedTree, il
metodo preorder(). Deve restituire in una
LinkedList i nodi dell’albero memorizzari
secondo la visita preorder.
Aggiungere, alla classe ArrayBinaryTree, il
metodo preorder(). Deve restituire in una
LinkedList i nodi dell’albero memorizzari
secondo la visita preorder.
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
25
Esercizi
Il metodo preorder() restituisce quello che è
ritornato dalla funzione treePreorder(root(),L)
LinkedList treePreorder(TreeNode v, LinkedList L) è
la funzione che realmente visita l’albero ed
inserisce i nodi incontrati nella lista L
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
26
Gerarchia completa
Aggiungere a LinkedBinaryTree il metodo
toString() che restituisce il contenuto
dell’albero rappresentato tramite una stringa
– toString() può essere implementato tramite una
visita
Aggiungere a LinkedBinaryTree il metodo
eval() che restituisce il risultato della
valutazione
dell’espressione
aritmetica
rappresentata dall’albero
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
27
Prof. Carlo Blundo
Laboratorio di Algoritmi e Strutture Dati
28
5












