anodo catodo

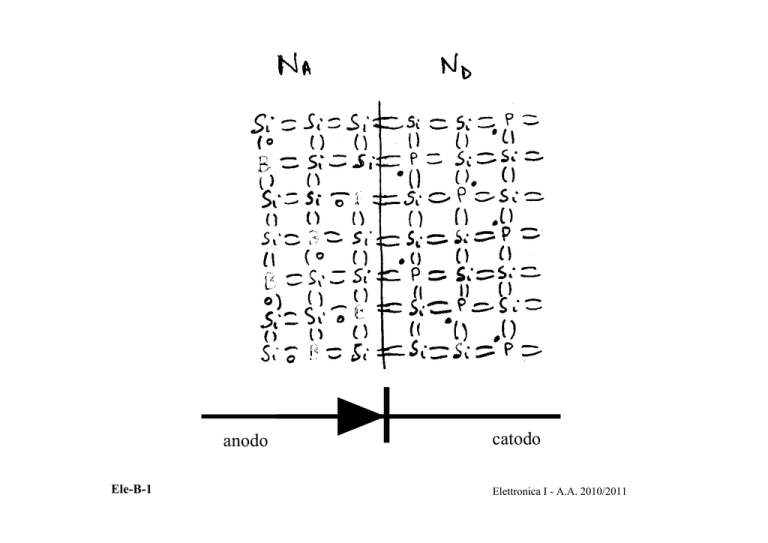
anodo
Ele-B-1
catodo
Elettronica I - A.A. 2010/2011
ASSENZA DI POLARIZZAZIONE
ND
NA
-
p
+
+
+
+
+
+
n
 (densità di carica)
qND
Wn
-Wp
x
ND Wn = NA Wp
-qNA
E (campo elettrico)
-Wp
Wn
x
Ele-B-2
Elettronica I - A.A. 2010/2011
Giunzione p-n in polarizzazione inversa: il
potenziale applicato dall’esterno (V) si
somma al potenziale interno di built-in
(Vo) (infatti il campo elettrico interno è
concorde con quello applicato dall’esterno)
Giunzione p-n in polarizzazione
diretta:
il
potenziale
applicato
dall’esterno (V) si sottrae al potenziale
interno di built-in (Vo) (infatti i campi
elettrici non sono concordi)
La barriera di potenziale interna diventa:
Vo+V
La barriera di
diventa: Vo-V

nel dispositivo non circola corrente
Ele-B-3
potenziale

nel dispositivo circola corrente
Elettronica I - A.A. 2010/2011
interna
CORRENTE IN UN DIODO P-N IN POLARIZZAZIONE DIRETTA
Per effetto della riduzione della barriera di potenziale, si determina un
flusso netto (iniezione) di lacune che attraversano la giunzione dal lato p al
lato n, e di elettroni che attraversano la giunzione nel verso opposto.
I due flussi danno vita ad una corrente Ipn di lacune minoritarie nel lato n e
ad una corrente Inp di elettroni minoritari nel lato p. Tali correnti hanno
verso concorde.
Queste correnti hanno in pratica la sola componente diffusiva. Infatti la
componente di trascinamento è trascurabile essendo E  0 al di fuori della
regione di carica spaziale.
Ele-B-4
Elettronica I - A.A. 2010/2011
Si definisce tensione di soglia
quella tensione V tale che:
I MAX
I V  
100
V,Ge  0.2 V
V,Si  0.6 V
V,GaAs  1.1 V
J. Millman - C.C. Halkias “Microelettronica” Ed. Boringhieri
Ele-B-5
Elettronica I - A.A. 2010/2011
Più in generale la corrente in un diodo vale:
 VV

I  I o  e T  1




 è detto fattore di idealità del diodo
1  2
Poiché ni è funzione della temperatura, la corrente di saturazione inversa
aumenta con con T:
I 0 (T )  I 01  2
Ele-B-6
T T1
10
Elettronica I - A.A. 2010/2011
CAPACITA’ DI GIUNZIONE
+V
p
n
W
Alla carica fissa presente nella regione di carica spaziale è associabile una
capacità detta capacità di giunzione o di transizione. Al contrario di un
normale condensatore, questa capacità è una funzione del potenziale applicato.
Si definisce quindi una capacità incrementale:
C j  dQ
A
  Si
dV
W
Una variazione dV del potenziale applicato determina una corrente ai terminali:
dQ
dV
i
 Cj
dt
dt
Ele-B-7
Elettronica I - A.A. 2010/2011
diodi VARICAP o VARACTOR
Ele-B-8
Elettronica I - A.A. 2010/2011
La corrente in un diodo è proporzionale all’accumulo di portatori
minoritari in eccesso.
L’accumulo di portatori minoritari determina la nascita di un’altra
capacità, detta capacità di diffusione, CD.
dQ
dI
I
p
p
CD 
dV
dV
VT
In polarizzazione diretta: CD >> CJ , in polarizzazione inversa: CD << CJ
Ele-B-9
Elettronica I - A.A. 2010/2011
Ele-B-10
Elettronica I - A.A. 2010/2011
Fig. 3.19 Graphical analysis of the circuit in Fig. 3.18.
Ele-B-11
Elettronica I - A.A. 2010/2011
26
Fig. 3.1 The ideal diode: (a) diode circuit symbol; (b) i-v characteristic; (c) equivalent circuit in the reverse direction; (d) equivalent
circuit in the forward direction.
Ele-B-12
Elettronica I - A.A. 2010/2011
15
Fig. 3.3 (a) Rectifier circuit. (b) Input waveform. (c) Equivalent circuit when (d) Equivalent circuit when v1  0 (e) Output
waveform.
Ele-B-13
Elettronica I - A.A. 2010/2011
16-24
Fig. 3.23 Development of the constant-voltage-drop model of the diode forward characteristics. A vertical straight line (b) is used to
approximate the fast-rising exponential.
Ele-B-14
Elettronica I - A.A. 2010/2011
29
=
Fig. 3.24 The constant-voltage-drop model of the diode forward characteristic and its equivalent circuit representation.
Ele-B-15
Elettronica I - A.A. 2010/2011
30
Fig. 3.20 Approximating the diode forward characteristic with two straight lines.
Ele-B-16
Elettronica I - A.A. 2010/2011
27
CARATTERISTICA LINEARE A TRATTI DEL DIODO
Per V < V il dispositivo è
un circuito aperto :
V  V
 I 0
Per V > V Il dispositivo è
una resistenza di valore Rf :
V  V
Ele-B-17
 I
V  V
Elettronica I - A.A. 2010/2011
Rf
=
Fig. 3.21 Piecewise-linear model of the diode forward characteristic and its equivalent circuit representation.
Ele-B-18
Elettronica I - A.A. 2010/2011
28
SIMBOLOGIA
IA, iA, ia
vA = tensione totale
VA = componente fissa (DC) della tensione
va = componente variabile (di segnale o AC)
della tensione
A
VA, vA, va
iA = corrente totale
IA = componente fissa (DC) della corrente
ia = componente variabile (di segnale o AC)
della corrente
Ele-B-19
31-I
Elettronica I - A.A. 2010/2011
Fig. 3.25 Development of the diode small-signal model. Note that the numerical values shown are for a diode with n = 2.
Ele-B-20
Elettronica I - A.A. 2010/2011
31
ID  ISe
In assenza di segnale variabile vd(t) si ha:
VD
nVT
In presenza del segnale variabile vd(t) si ha:
iD  I S e
Se vd(t) << n VT :
VD  v d
nVT
 ISe
VD
nVT

vd
iD  I D 1 
 nVT
e
vd
nVT
 I De
vd
nVT

ID
  I D 
vd  I D  id
nVT

nota come “approssimazione a piccolo segnale”
nVT
dvD
 rd 
ID
diD
Ele-B-21
31-II
resistenza differenziale del diodo valutata alla corrente ID
Elettronica I - A.A. 2010/2011
Nell’approssimazione a piccolo segnale, la caratteristica del diodo è sostituita,
nell’intorno del punto di funzionamento, dalla retta tangente:
1
iD  vD  VD 0 
rd
che è la caratteristica del bipolo:
Dal circuito si ottiene:
vD  VD 0  iD rd 
 VD 0  I D rd  id rd  VD  id rd
e cioè la componente continua (DC) della tensione
sul diodo può essere calcolata da:
VD  VD 0  I D rd
mentre la componente variabile (AC) può essere
calcolata da:
vd  id rd
Ele-B-22
31-III
Elettronica I - A.A. 2010/2011
In sostanza, per il calcolo della componente continua ci si può servire del circuito:
infatti in questo circuito:
VD  VD 0  I D rd
dove però occorrerebbe conoscere rd .
Pertanto nella maggioranza dei casi si
adotta l’approssimazione:
VD  VD 0  0.7 V
Invece per il calcolo della componente variabile ci si serve del circuito:
in cui infatti:
con:
Ele-B-23
rd 
vd  id rd
 VT
ID
Elettronica I - A.A. 2010/2011
DIODI A BREAKDOWN A VALANGA O ZENER
Per qualsiasi diodo polarizzato inversamente esiste una tensione VZ di breakdown oltre
la quale la corrente inversa aumenta rapidamente. Se il diodo non è progettato
opportunamente, il surriscaldamento che ne consegue ne determina la distruzione.
I meccanismi responsabili di questo fenomeno sono due, ed in genere agiscono in
maniera indipendente:
1) rottura Zener: il campo elettrico nella
regione di svuotamento supera il valore oltre il
quale si ha la ionizzazione diretta degli atomi
di silicio (0 < VZ < 8 V)
2) ionizzazione da impatto, o scarica a
valanga: il campo elettrico nella regione di
svuotamento accelera i portatori che, urtando
contro gli atomi del cristallo, li ionizzano
producendo altre coppie e-h. Queste a loro
volta sono accelerate e producono in cascata
altre coppie e-h (VZ > 6 V)
Ele-B-24
Elettronica I - A.A. 2010/2011
Fig. 3.31 The diode i-v characteristic with the breakdown region shown in some detail.
Ele-B-25
Elettronica I - A.A. 2010/2011
34-35
Fig. 3.32 Model for the zener diode.
Ele-B-26
Elettronica I - A.A. 2010/2011
36
Fig. 3.36 Block diagram of a dc power supply.
Ele-B-27
Elettronica I - A.A. 2010/2011
37
Fig. 3.37 (a) Half-wave rectifier. (b) Equivalent circuit of the half-wave rectifier with the diode replaced with its battery-plusresistance model. (c) transfer characteristic of the rectifier circuit. (d) Input and output waveforms, assuming that rD  R.
Ele-B-28
Elettronica I - A.A. 2010/2011
38
Fig. 3.39 The bridge rectifier: (a) circuit and (b) input and output waveforms.
Ele-B-29
Elettronica I - A.A. 2010/2011
40
Fig. 3.41 Voltage and current waveforms in the peak rectifier circuit with CR  T. The diode is assumed ideal.
Ele-B-30
Elettronica I - A.A. 2010/2011
41
CALCOLO DELL’INTERVALLO DI CONDUZIONE DEL DIODO
Il diodo comincia a condurre all’istante –tc
e si spegne in t=0.
Vr
–tc è l’istante in cui:
VP cos  tc   VP  Vr
 1
2
VP 1   tc    VP  Vr
 2

Vr
 tc  2
Vp
Quindi tc è piccolo se si richiede un “ripple” piccolo
Ele-B-31
41-II
Elettronica I - A.A. 2010/2011
Ele-B-32
41-III
Elettronica I - A.A. 2010/2011
CALCOLO DELLA CORRENTE MEDIA NEL DIODO
DURANTE L’INTERVALLO DI CONDUZIONE
Ele-B-33
41-IV
Elettronica I - A.A. 2010/2011
Uso di diodi Zener per la stabilizzazione della tensione sul carico
Obiettivo: rendere Vo indipendente da vs (variazioni della
tensione di alimentazione) e da RL (variazioni del carico)
Per lo studio della dipendenza da RL, esaminando il
circuito per le componenti DC si ottiene:
Del diodo Zener sono note rz e Vz
Se si sceglie R<<RL si ottiene:
Ele-B-34
VS
RL  VZ
R  RL
Vo 
rZ  VZ
R RL
 rZ
R  RL
VS  VZ
Vo 
rZ  VZ
R  rZ
e dunque tensione sul
carico indipendente dal
carico stesso
Elettronica I - A.A. 2010/2011
Uso di diodi Zener per la stabilizzazione della tensione sul carico
(2)
Per lo studio della dipendenza da vs, esaminando il circuito
per le sole componenti AC si ottiene:
vs
vs
RL rz  
vo 
rz
R  RL rz 
R  rz
in quanto rz è in genere molto più piccola di RL (alcuni )
Del diodo Zener sono note rz e Vz
Se poi si sceglie R>>rz , vo tenderà ad annullarsi.
Come regola di massima, conviene scegliere R in modo tale che IZ  10  IRL ,
ed inoltre dovrebbe risultare:
RL  R  rz
Ele-B-35
Elettronica I - A.A. 2010/2011