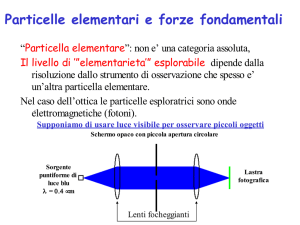
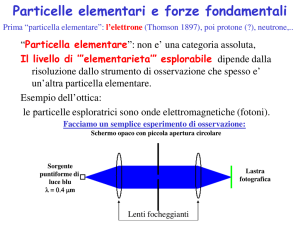
Particelle elementari e forze fondamentali
“Particella elementare”: non e’ una categoria assoluta,
l’”elementarieta’” dipende dallo strumento di osservazione
che spesso e’ un’altra particella elementare:
Risoluzione spaziale
energia dell’interazione
Con la luce in un microscopio abbiamo una risoluzione ∆r:
θ
∆r~λ/sinθ, nel caso di particelle: λ=h/p
∆r~λ/p sinθ ~ h/q
con q impulso trasferito nell’interazione. Piu’ é grande l’impulso
Trasferito maggiore é la risoluzione (potere separatore).
Aumentando l’energia dell’interazione abbiamo scoperto vari
“stati elementari”:
-Atomi (Democrito) e molecole (elementi chimici 1700-1800)
-Struttura atomica : fisica atomica (Rutherford inizio 1900)
E d KeV, rt10-8 cm
-Struttura del nucleo:fisica nucleare, anni 30, protoni e neutroni
E~MeV, r~10-13cm
-Struttura dei nucleoni: fisica subnucleare, dagli anni 50.
E > GeV, r < 10-13cm
Oggi disponiamo di ‘microscopi’ in grado di far interagire
le particelle con energie di TeV
Particella elementare
-Non ha struttura interna: e’ caratterizzata solo da una massa, carica
elettrica, spin (momento magnetico).
-Non ha dimensione: dd10-18 m.
Ex: distribuzione di carica di un elettrone ρ(r)=q δ(r)
distribuzione di carica di un protone: ρ(r)=(q /r0) exp(-r/r0) (r0~ 0.2 10-13cm)
-.Non ha stati eccitati.
Se l’energia dell’interazione e’ sufficiente si possono creare nuove
particelle, Ex : e+ e- π+ π− se s ≥ 2mπ , µ−
e- νµ νe
I fenomeni sperimentali sono inquadrati teoricamente in una:“Teoria
quantistica di campo” che incorpora sia la relativita’ che la meccanica
quantistica: quantizzazione del campo mediatore dell’interazione.
Particelle elementari oggi conosciute
a 10-18 m (103 GeV)
− 6 leptoni + 6 quark tutte a spin ½ e con “masse” che vanno da
0.5 MeV/c2 a 175 GeV/c2
−4 interazioni fondamentali:
1) gravitazionale;
Intensita’
2) debole;
crescente
3) elettromagnetica;
4) forte.
i quark sono soggetti a tutte e 4 le interazioni mentre
i leptoni sperimentano solo le prime 3.
Simmetrie
Simmetrie di spazio tempo
Parita’
P
Parita’ intrinseca
P
Inversione temporale T
Simmetrie interne
Isospin
I
Coniugazione di carica C
G parita’
G
Simmetrie locali della lagrangiana (gauge)
Generazione delle interazioni tra le particelle
i mediatori
Simmetrie
convervazione di osservabili fisiche (Noether)
Ex: in elettrodinamica: invarianza per cambiamento locale della fase:
ψ → eiϑψ (gruppo U(1))
conservazione della carica elettrica
Applicata alla lagrangiana dell’elettrone libero genera un campo vettoriale
il fotone e la QED
mediatore:
-Quali altre simmetrie (e mediatori) per le altre interazioni?
-Si possono unificare le 4 interazioni e sotto quale simmetria?
Oggi disponiamo di:
-Teoria unificata elettrodebole validata dalla scoperta di W/Z, quark top, molte
misure di precisione. Manca pero’ ancora un elemento: il bosone di Higgs
(scoperto nel 2007 ?)
-Teoria delle interazioni forti la QCD (simile alla QED)
-Ma la gravita’!?
Fisica delle particelle, cosmologia e astrofisica
Si va sempre piu’ consolidando il legame tra la fisica delle particelle e la
fisica del cosmo: l’origine e l’evoluzione dell’universo e la fisica delle
galassie e delle stelle (astrofisica) dipendono in maniera cruciale dalle
particelle e dalle loro caratteristiche e interazioni. Ex.
Il numero dei neutrini e la loro massa,
il problema della materia oscura,
l’origine dei raggi cosmici,
la stabilita’ della materia,
…
Il sole come laboratorio delle
4 forze
-Inizialmente condensazione gravitazionale da una nuvola di idrogeno fino a
una temperatura di 107 K: innesco della fusione termonucleare.
-Prima reazione di fusione e’ debole: pp
d+e++νe (“lenta”)
-Gli stadi successivi coinvolgono reazioni forti e elettromagnetiche ex:
p+d
3H +γ
e
L’energia liberata si trasmette essenzialmente come raggi X dal
centro del sole alla fotosfera con interazion elettromagnetiche
ma anche come radiazione di neutrini che trasportano
una frazione significativa di tutta l’energia emessa dal sole
Super-Kamiokande: Neutrini solari
νx + e− → νx + e− : energia di soglia: 5 MeV, sensibile ai neutrini solari del B
I neutrini vengono dal sole
Foto del sole con i neutrini
Il sistema di unita’ naturali i.e. c = 1, h = 1
Nel SI, c=2.998 108 m/s e h = 1.055 10-34 J s, 1 GeV= 1.6 10-10 J
−massa (mc2) e impulsi (pc) in GeV. Ex mp=1.7 10-27Kg=0.938 GeV
-lunghezza ( λC = h mc ) in GeV-1 ex 1 GeV-1 =0.197 10-13cm=0.197 fm
-aree in GeV-2 ex 1 GeV-2 =0.0388 fm2=0.388 10-27cm2=0.388 mbarn
-tempi (t=λc/c) GeV-1 ex 1 GeV-1=6.57 10-25 s
-forza: F=ma=mlt-2 = m2 i.e. GeV2
ex:1dyne=gr cm/s2=1.24 10-11 GeV2
q
ex: potenziale quark-antiquark (quarkonio):
a
V (r ) = br − + V0
r
q
Se b=0.18 GeV2 F=15 ton; se r=1fm ~ 5 GeV-1, V(r) = 0.9 GeV
q
q q
q
mπ=0.14 GeV
Ex. hc= 197 MeV fm (1 fm= 10-15m)
e2 1 e2
S .I . EC =
⇒
= MeV ⋅ fm ⇒
4πε 0 r
4πε 0
e2
1
e' adimensionale =
≡α
137
4πε 0 hc
ze
Ze
θ
Ex: scattering Rutherford:
σ (θ > θ ) =
πz 2 Z 2
4
=
e2 2 1
[
] 2
4πε0 T
πz 2 Z 2 1
4
1
tan
2
θ
=
πz 2 Z 2
2
197 2 2
[
][
] fm
137 T (MeV )
2
hc 2
α ( )
T
4
2
1
tan
2
θ
2
1
tan
2
θ
2
Se T= 1 MeV, θ = π/2, σ(θ>π/2)= 1.6 fm2, se z=1, Z=1
=
Per la sezione d’urto differenziale abbiamo (formula di Rutherford):
2
dσ ( Zz )
197
1
2
−1
=
sr
(fm
)
θ
dΩ
16 137 ⋅ T ( MeV ) sin 4
2
2
Ex. σ(Thomson) Eγ<<me
8 α2 8
σ (γe → γe) = π 2 = π ⋅ re2 = 0.7 barn
3 me 3
µ+µ− se s>>mµ2
Ex. Interazione e+e-
4 α2
s = ( p1 + p2 ) 2
σ (e e → µ µ ) = π
3 s
+ −
Se siamo nel c.m. e+
+
−
e-, se E(e+)=E(e-)= 1 GeV. s= 4 GeV2
2
4 1
1
−33
2
σ (e + e − → µ + µ − ) = π
⋅
=
2
.
1
⋅
10
cm
= 21 nb
2
3 137 4GeV
Forza gravitazionale
Potenziale Newtoniano:
V = GN
m 2p
r
GN = 6.67 ⋅10 −11 m 3 Kg −1s −2 = 4.17 ⋅10 −5 GeV ⋅ cm / gr 2 =
= 0.67 ⋅10 −38 GeV − 2 (incertezza ≈ 130 ppm)
se m p = massa protone ≈ 1 GeV
r = 10 −13 cm ≈ 1 fm ≈ 5GeV −1 ⇒ V ≈ 10 −39 GeV
1 e 2 hc
0.197 ⋅ GeV ⋅ fm
nel caso Coulombiano V =
=α
≈ 1.4 ⋅10 −3 GeV
4πε 0 r hc
1 fm
⇒ su scala microscopica (fm) la gravita' e' totalmente trascurabile
Notiamo:
1
GN ≡
≈ 0.8 ⋅10 −19 GeV −1 = 5.3 ⋅10 − 44 s = 1.6 ⋅10 −33 cm
MP
1
GN
≡ M P ≈ 1019 GeV (massa di Plack)
L’interazione gravitazionale diventa significativa (paragonabile
alle altre) a energie (masse) dell’ordine di MP oppure a distanze
r~10-33cm.
Se assumiamo che l’intensita’ dell’interazione gravitazionale sia come quella
elettromagnetica alla massa di Planck quanto vale la corrispondente costante
di accoppiamento gravitazionale, αGN, a basse energie (1GeV)?:
α GN
2
1GeV
−38
− 40
~
α ≈ 10 α ≈ 10
2
MP
Forza nucleare debole
Responsabile della radioattivita’ decadimento beta:
n
p+e-+νε
Ο14
Ν14+e+ νe (Τ1/2=71.4 s)
Dalla vita media si estrae la costante di accoppiamento
1
T = ∝ GF2
Γ
GF~10-5GeV-2
1
≈ 300GeV
GF
GF ≈ 0.7 ⋅10 −13 cm
Scala a cui le interazioni debole diventano significative.
paragonabili a quelle elettromagnetiche
A 1 GeV:
(1GeV ) 2
−5
−7
αW =
α
≈
10
α
≈
10
(300GeV ) 2
Forza elettromagnetica
Potenziale Coulombiano:
V=
e2
4πε 0 r
Ex. Nell’atomo di idrogeno l’energia di legame (formula di Bohr):
1 2
E1 = α ( µc 2 ), µ = massa ridotta ≈ m e , α = 1 / 137
2
E1 ≈ 14eV
Per un sistema legato p p , µ=mp/2=1000 me
E1 ≈ 14KeV
La forza dell’interazione e’ determinata da α
Forza nucleare forte
L’energia di legame elettromagnetica p p ~ 14 KeV ma se
prendiamo un sistema simile: il deutone : (pn) l’energia
di legame e’ molto piu’ grande ~ 2 MeV
la costante di accoppiamento delle interazioni forti αS
(e il deutone e’ un sistema legato per interazione forte):
αS~100 α (confinata entro r~10-13cm)
L’intensita’ relativa delle 4 forze vale:
10-40
10-7
10-2
1
Unificare la gravita?
GN m 2
2
2
F ≡ GeV , FN =
≡
GeV
,
abbiamo
gia'
visto
G
≡
1
/
GeV
N
2
r
1 / GN = M P ≈ 1019 GeV
2
Il flusso del campo gravitazionale H in 3 dimensioni vale:
Φ ( H ) = 4π ⋅ r 2 ⋅ H = m ⋅ GN ⇒ H ∝ GN / r 2
Teorema di Gauss in 3+d dimensioni:
H’=GD/r2+d
Con GD=
“costante di gravita’ in 3+d dimensioni”
Ma H’ deve avere le stesse dimensioni di H quindi se
GN = 1 / M P2 , GD = 1 / M D2+ d , ma H = H' (almeno a grandi distanze) ⇒
GN
1
1
GD
= 2 2 = 2+ d = 2+ d 2+ d
2
r
M Pr
r
MD r
Da cui MP2=MD2+d rd,
con d la dimensione degli spazi extra
Vogliamo unificare la gravita’ con l’interazione elettrodebole:
MD=1 TeV
32
2
M
r d = 2P+ d = 1032 (TeV ) − d ⇒ r = 10 d TeV −1
MD
Se d=2 r=1016 TeV-1= 2mm !!
La forza di gravita’ e’ cosi’ “debole” perche’ “diluita” nelle
extra dimensioni
Si dovrebbero osservare deviazioni alla gravita’ Newtoniana
a distanze ~ r (esperimenti di microgravita’)
Raggio di azione delle forze
A
A
X
B
t
A+B
A+B
B
Possiamo schematizzarlo come un “processo virtuale” con A che emette X
r
r
r
A( M A ,0) → A( E A , p ) + X ( E X ,− p )
con E A = M + p , E X = M + p
2
A
2
2
X
2
La differenza di energia finale-iniziale ∆E si puo’ scrivere come:
∆E = E X + E A − M A = M X2 + p 2 + M A2 + p 2 − M A > M X
Il processo puo’ avvenire solo se il tempo caratteristico τ vale:
h
h
τ≈
≤
∆E M X
La distanza massima di propagazione della particella X ,R vale:
hc
(range)
R = c ⋅τ ≤
MX
Se MX=0 (fotone) R
∞ , ma anche ∆Ε
0e τ
∞:
il fotone e’ reale
Nel caso di interazioni deboli MX=MZ=90 GeV.:
hc 0.197 ⋅ GeV ⋅ fm
=
~ 2 ⋅10 −3 fm
R≤
MZ
MZ
Se l’impulso p della particella A (o B) e’ tale che la lunghezza d’onda
De Broglie λΒ>>R, abbiamo in approssimazione di “interazione puntuale:
alla Fermi.
A
B
A
B
Nel caso di interazioni nucleari forti sappiamo che R~10-13cm da cui:
hc
MX ~
~ 100 MeV (Yukawa) Particella trovata nel 1947 (mesone π) con
R
Mπ=140 ΜeV.:
Ma questa tra nucleoni non e’ una forza veramente elementare…
Ordini di grandezza
Quantita’ fondamentali:
10 −5
1
m
, GF = 2 , me = 0.51 MeV , m p = 1800 me , mπ = p
=
α=
7
4πε 0 137
mp
e2
Raggio atomo di idrogeno:
Momemto angolare :
pr ~ 1 ⇒ p ~ 1 / r
Energia cinetica
p2
1
= 2
T =
2me 2 r me
−α
r
1
ET =
2 me
Energia coulombian a U =
Energia totale
Minimo di E T :
1 α
2 −
r r
∂ET
α
1
=0⇒
+
= 0 da cui :
∂r
me r 3 r 2
r = 1/αme = rB (raggio di Bohr) = 5 10-9 cm
In QED abbiamo 3 lunghezze fondamentali che differiscono di α:
Raggio di Bohr :
Lunghezza d’onda Compton:
Raggio classico elettrone:
rB= 1/αme ;
λc=1/me
re=α/me
Dimensioni degli adroni: se la costante di accoppiamento
forte αS~1 abbiamo solo una lunghezza caratteristica:
1/mπ ~ 0.8 fm ~ rp
(il π e’ il piu’ leggero degli adroni:mπ∼140 ΜeV)
Interazioni adroniche a grande energia, se rP~ 1 fm abbiamo:
rP
σ pp ≈ π ⋅ rp2 = 3 ⋅10 −26 cm 2 = 30 mb
Gli altri adroni sono mesoni composti da 2q (π,Κ) o barioni
composti da 3q. Quindi se σqq e’ la sezione d’urto qq mi aspetto:
σ(pp) = 3x3 σ(qq) ; σ(πp) = 2x3 σ(qq)
σ (πp ) σ ( Kp ) 2
~
~ ⇒ σ (πp ) = σ ( Kp ) ~ 20 ⋅ mb
σ ( pp ) σ ( pp ) 3
σ(pp) ~ σ(np) ~ σ(pp) ~ σ(np) ~ 40 mb
σ(πp) ~ 25 mb; σ(Κp) ~ 20 mb
Sperimentalmente:
Scarsamente dipendenti da
s , se s >> m p
Interazioni elettromagnetiche
a) e e → µ µ :
+ −
+
−
Unico invariante di Lorentz:
Per cui, dimensionalmente:
α
e-
q
t
e+
α
µµ+
r2
2
q = q − q = Ecm
≡s
2
σ =
2
0
α2
s
, se s >> m µ2
4π α 2
σ (vera) =
, se s = 1 GeV 2 , σ = 4 ⋅10 −32 cm 2
3 s
b) Scattering Compton : γ e → γ e
γ
e
α
α
q’
t
γ
e
σ=α2f(s,me), e sia Eγ l’energia del fotone:
1) Caso non relativistico: Eγ<<me (l’energia del fotone non cambia) e s ~ me2
α2
8π 2 8π α 2
σ = 2 , σ (vera) =
sezione d' urto Thomson
r0 =
2
3
me
3 me
2)Caso ultrarelativistico: s >> me2
α2
α2
s
, σ (vera) = 2π
ln 2
σ=
s
s m
La correzione logaritmica deriva da effetti di spin dell’elettrone e fotone:
ad alta energia prevale l’interazione magnetica (tra momenti magnetici).
νµ
Interazioni deboli
ν µn → µ − p
G
q
νµN → µ−X
n
G
µp
t
Ci aspettiamo: σ(νN)=G2 f(s,mN)
se s>>mN2, mN e’ trascurabile e, dimensionalmente essendo [G]=s-1:
lab
σ(νN) = G2s
= G2 mNEν ~ 10-10 Eν (GeV) GeV-2 ~ 4 10-38 Eν (GeV) cm2
σ(vera)= 0.6 10-38 Eν (GeV) cm2
Interazioni forti (scattering Compton forte)
π p → π p, σ Th
8π
=
3
2
αs
(*)
m
p
π
p
αS
t q’
αS
π
p
Ma sperimentalmente σ(πp)=2 10-26 cm2=5 10 (0.4 10-27 cm2) = 50 GeV-2
Per cui utilizzando la (*) α ∼ 2.4 !!!!
Problemi con la teoria delle perturbazioni: ex:
αS
αS
il processo O(αS3) non e’ un contributo di
ordine superiore!!
αS
Lo studio delle particelle elementari
attraverso misure:
• di scattering ex. eN
eN (struttura nucleone);
• stati legati ex. (e+e-) (livelli energetici, parita’…);
• vite medie di particelle instabili ex.
π+
µ+ νµ
µ−
e− ν e ν µ
Vita media
Particella instabile : P
a+b con una probabilita’ di decadere per unita’
di tempo ω, costante nel tempo. La variazione dn di popolazione n di P sara’:
dn = −n ⋅ ω ⋅ dt → n = n0 ⋅ e
−ω ⋅t
;
1
ω
≡ τ ≡ vita media della particella
L’incertezza sul tempo di decadimento implica anche
un’incertezza sull’energia dello stato (particella): ∆E=Γ:
∆E ≡ Γ = 1
τ
Γ ≡ larghezza della particella
ex. τ π ± = 2.6 ⋅10 −8 s ⇒
1
6.5 ⋅10 − 25
−17
Γπ ± =
=
GeV
≈
2
.
5
⋅
10
GeV
−8
−8
2.6 ⋅10 s 2.6 ⋅10
In termini di decadimento dello stato
r 2
r
2 − Γt
ψ (r , t ) = ψ (r , t = 0) e
r
ψ (r , t )
e la funzione d’onda ψ:
r
r
ψ ( r , t ) = ψ ( r , t = 0) ⋅ e
−
Γt
2
⋅ e − m0t (*)
Dove ei m t descrive l’evoluzione di uno stato stazionario (ω=0) di massa m0:
0
r
r
∂ψ
− im0t
ψ ( r , t ) = ψ ( r , t = 0) ⋅ e
(soluz. eq. di Schroedinger con H = m0 :
= −iHψ )
∂t
Facciamo la trasformata di Fourier della (*):
ψ ( m) =
1
2π
∫
∞
0
r
r
1
ψ (r , t = 0)
dt ⋅ e imtψ (r , t ) =
;
Γ
2π − + i (m − m )
0
2
Facendo il modulo quadro e integrando sulla parte spaziale (normalizzata a 1)
1
1
ψ =
2π Γ 2 / 4 + (m − m0 ) 2
2
Quindi la probabilita’ di osservare lo stato a una massa m vale:
1
Γ
P(m)dm =
dm
2
2
2π Γ + (m − m0 )
4
∞
(con la normalizzazione : ∫ P(m)dm = 1)
0
P(m)
La larghezza a meta’ altezza Γ
e’ una misura dell’intensita’della
interazione che ha prodotto il
decadimento
m0
m
ex. Γ( ρ ± → π ±π 0 ) = 150 MeV (interazioni forti)
Γ(π 0 → γγ )
Γ(π ± → µ ±ν )
= 8 ⋅10-6 MeV (interazioni elettromagnetiche)
= 2 ⋅10-14 MeV (interazioni deboli)
Attenzione: Γ e’ determinata anche dal numero di stati finali disponibili
(spazio delle fasi). Ex: Γ(W) ~ 2.1 GeV (interazione debole), ma il W(m=80 GeV)
decade in coppie di quark o leptoni che hanno m<<mW con un grande spazio
delle fasi e quindi grande probabilita’ di decadimento (larghezza).
Le prime particelle elementari
• Anni 30: p, e-, n, γ, e+ (antiparticella dell’elettrone predetta
teoricamente da Dirac nel 1931). Stabili eccetto il neutrone.
• Anni 40: π+−, π0, µ+−, con la corretta sequenza di decadimento:
π+−
µ+−ν
e+- ν ν
Instabili : τ π ± = 2.6 ⋅10 −8 s; τ µ ± = 2.2 ⋅10 −6 s; τ π 0 = 8.7 ⋅10 −17 s
spin π ± , π 0 = 0; spin µ ± , e ± = 1
2
Anni 50-60: altre particelle a vita media breve (10-23-10-25s)
e spin 1: ω,ρ che decadono in π: ρ
ππ, ω
π+π−π0
Ma anche particelle che decadono in π ma con vita media lunga
(10-8-10-10s) e per questo chiamate strane:
π +π0, Κ+
µ+ν, Κ0
π+π−, Λ
π−p
Κ+
Ma sono tuttavia prodotte in coppia nelle interazioni forti ex:
π−p
Κ 0Λ
Idea: associare a queste particelle strane un nuovo numero quantico“la stranezza”
che si conserva in produzione (forte) ed e’ violato nel decadimento (debole).
. Anni 70-80. Il fenomeno delle particelle “strane” si replica con altri adroni
ancora piu’ pesanti: ex: D+-, D0 (m~2 GeV), Λc; B+-., B0 (m~5 GeV), Λb
Introduzione di altre “qualita’”che caratterizzano la materia adronica:
charm (c) , beauty (b)
Anni 90: scoperto l’ultimo stato degli adroni: top (t) (m ~ 175 GeV),
ma non ha stati legati!!
Questi numeri quantici sono manisfestazioni di gradi di liberta’ interni
degli adroni (i costituenti): i quark. Modello:
u
d
c
s
t
b
Q = 2/3
Q = -1/3 + antiquark, tutti a spin = 1/2
Gli adroni misurati non sono elementari ma composti da quark:
[q q]: mesoni a spin intero ex. π+=[u d], π−=[u d], π0=[u u + d d]
[q q q]: barioni a spin semintero ex. p=[u u d], n=[u d d]
Sezione d’urto
Misura ‘l’intensita’ della interazione: consideriamo ad es. la reazione:
a+b
c+d
Flusso di particelle a sulle particelle bersaglio b:
Se la densita’ di particelle incidenti e’
ρa e la velocita’ vi, il flusso incidente sara’:
S
a
ρa
vi
σ
Φ=ρa vi
b
dx
La densita’ di bersagli e’ ρb e ciascuno copre un’area σ, il numero di interazioni
per unita’ di tempo e di area, R sarà:
R = Φ ⋅ σ ⋅ ρ b ⋅ dx = ρ a ⋅ vi ⋅ σ ⋅ ρ b ⋅ dx
Sul volume dV=S dx avro’ un numero di interazioni totali al secondo: dN/dt :
dN
= ρ a ⋅ vi ⋅ ρ b ⋅ σ
dtdV
Integrando sul tempo e sul volume (su dx) otteniamo il numero N di interazioni:
na ⋅ nb
N = nb ⋅ ρ a ⋅ ∫ vi dt ⋅ σ =
σ;
S
na/S= particelle incidenti per unita’ di superficie;
nb= numero totale di bersagli b
Se N = numero di Avogadro;
A= peso atomico;
ρ= densita’ del bersaglio
Da cui:
N = na
ρVN
AS
nb =
A
nb' (nucleoni) = ρVN
Mb
Nσ
AS
σ = na
ρVN
con M b = massa del bersaglio
n n
Riscriviamo N: N = a b ⋅ V ⋅ σ Se T e’ il tempo totale di misur e Φa=na/S
S V
Φa
N=
⋅ ρb ⋅V ⋅ T ⋅ σ = f ⋅ ρb ⋅V ⋅ T ⋅ σ
T
Φa
con f =
T
Vogliamo passare dal lab a un riferimento qualsiasi; nota che VT e N sono
invarianti di Lorentz; vogliamo che anche f ρb lo sia.
Partiamo dall’invariante:
ρ a ρb F =
Che si riduce a f ρb nel lab dove
ρ a ρb
( pa ⋅ pb ) 2 − (ma mb ) 2
ma mb
[ ]
r
r
pa = [Ea , pa ] , pb = mb ,0
r
r
r
r
Nel centro di massa di a e b (cms): pa = − pb e definiamo pa = pb ≡ q
F=
q ( Ea + Eb ) q s
=
, con s = (pa + pb ) 2
ma mb
ma mb
Occorre definire ρα e ρb. E’ conveniente scegliere la cosiddetta “normalizzazione
covariante” della funzione d’onda tale che
3
assicura che la densita’ di volume sia la
V =1
stessa in ogni sistema di Lorentz.
∫
ρ ⋅ d x = 2E
Se ρa,ρb sono le densita’ nel sistema di riposo: ρa=2ma, ρb=2mb, da cui:
ρ a ρ b F = 4ma mb
q s
= 4q s e nel cms N = 4q s ⋅ V ⋅ T ⋅ σ E il rate R (eventi/tempo)
ma mb
( E + Eb )
N
R = = ρ a ρb q a
V }⋅ σ ≡ L ⋅ σ
T
ma mb
L e’ definita come la luminosita’ del sistema e ha dimensioni cm-2s-1
( Ea + Eb ) 2
1
q
q
+γb
]=
L = ( ρ a ρb q
V ) = ρ aVρ bV [γ a
ma mbV
V
mb
ma
1
ρ aVρ bV γ aγ b [ β a + β b ]
V
con γ a,b =
E a ,b
ma ,b
e β a,b =
q
γ a ,b ma ,b
Se le particelle sono contenute in due pacchetti di sezione S e lunghezza l:
l
volume del pacchetto
S
nel suo sistema di
riferimento
L = ρ aγ aV ρ bγ bV
Ex. na= nb= 1010
l = 10 cm
S = 1 mm2
βa= βb = 1
βa βb
βa + βb
lS
= na nb
βa + βb
lS
L = 2 1031 cm-2 s-1
Questa, tuttavia e’ una luminosita’ istantanea: definisce il rate nel tempo
T=l/(βa+βb) di attraversamento dei due pacchetti.
In genere l’acceleratore e’ circolare con K pacchetti
per ciascun fascio e il rate R al secondo e’:
R = na ⋅ nb ⋅
βa + βb
lS
l
⋅
⋅ σ⋅ K⋅ f
βa + βb
K
K
Luminosita’ integrata sul
tempo di attraversamento
Luminosita’ al secondo:
se na e nb non sono uniformi ma
distribuite gaussianamente con
larghezze σx σy
Frequenza di
rivoluzione
na nb
L=
K⋅ f
S
L=
na nb
4πσ xσ y
K⋅ f
Ex. LEP : na = nb (e+ e-) = 5 1011, f = 104, K = 4, σx ∼ 2 10−2 cm , σy ∼ 8 10−4 cm
σ(e+ e-
L ~ 3 1031 cm-2 s-1
Z) ~ 50 nb = 5 10-32 cm2 (~ 10-1 Z al secondo)
Ex. LHC : na = nb (p p) = 1011, f = 104, K = 2800, σx ∼ σy ∼ 1.5 10−3 cm
L ~ 1034 cm-2 s-1
σ(pp
H) ~ 1pb = 10-36 cm2 (~ 10-2 H al secondo)
Ma σtot(pp) ~ 100 mb = 10-25 cm2
Rtot ~ 109 al secondo
Si introduce anche una luminosita’ integrata:
N = σ ∫ Ldt ( ∫ Ldt ha dimensioni di cm -2 )
La luminosita’ integrata si misura in µb-1, nb-1, pb-1, fb-1, …
∫
Ex. Se Ldt
=105 pb-1 ( 1 anno a LHC), per un processo con sezione d’urto
σ = 1 pb avro’ N= 105 pb-1 1 pb = 105 eventi
Ulteriore problema a alta luminosita’ e alto rate
A LHC σT = 100 mb e se L= 1034 cm-2 s-1, R= 109/s
Ci sono ~ 3000 pacchetti per fascio
tempo intercorrente tra due
attraversamenti successivi di pacchetti (bunch crossing) e’ 25 ns
Numero di eventi medio per bunch crossing NBC:
NBC = 109 25 10-9 = 25
p
p
15 µm
7 cm
Risultato: 25 eventi prodotti entro 25 ns (distribuiti poissonianamente) e
~ 25 x 30 ~ 1000 particelle cariche prodotte (+ quelle neutre) ogni 25 ns.
Le interazioni a LHC appariranno cosi:
A simulated event in ATLAS (CMS)
H
ZZ
4
34 cm-2 s
-1, bunch
pp collisions at
= 14 TeV L = 10
spacing 25 ns
inel. 70 mb
Interested in processes
with
fb
23 overlapping minimum bias events / BC
1900 charged + 1600 neutral particles / BC
Energia del fascio di LHC : ~ 300 MJ