Document

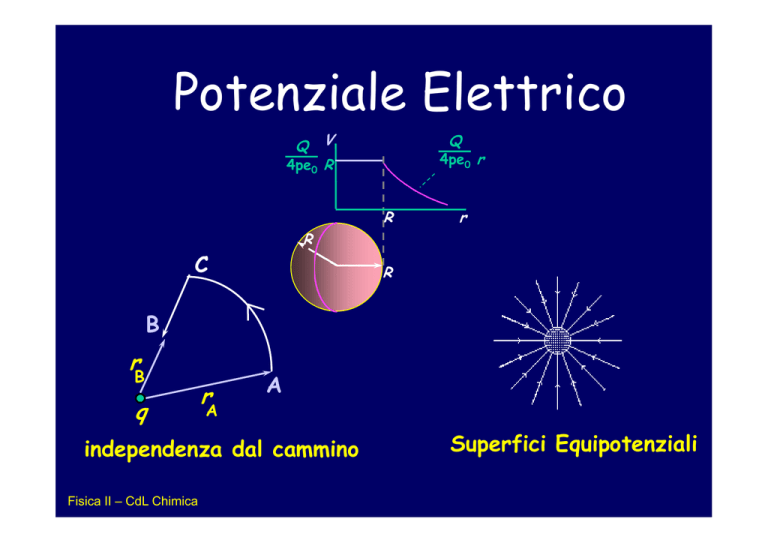
Potenziale Elettrico
Q
V
Q
4pe0 r
4pe0 R
R
r
R
C
R
B
r
B
q
r
A
A
independenza dal cammino
Fisica II – CdL Chimica
Superfici Equipotenziali
• Due modi per analizzare i problemi
– Con le forze o i campi (vettori) per determinare
posizione e velocità di un corpo in moto.
– Con l’energia (scalare) per determinare l’evoluzione di
un sistema da uno stato iniziale ad uno finale.
Energia Potenziale Elettrica
L’energia potenziale elettrica
di un sistema di particelle
puntiformi fisse è uguale al
lavoro che un agente esterno
deve fornire per aggregare il
sistema stesso.
b
b
rb
a
a
ra
ΔU = − ∫ Fids = − ∫ Fdr = ∫
⎛1 1⎞
ΔU = U b − U a =
q1q2 ⎜ − ⎟
4πε 0
⎝ rb ra ⎠
1
Fisica II – CdL Chimica
q1q2
dr
2
4πε 0 r
1
Forze Conservative e Conservazione Energia
• l’energia totale è costante ed è la somma di energia
cinetica e energia potenziale
Conservazione energia meccanica di una particella
1
− Energia Cinetica non-relativistica
K = mv 2
2
− Energia Potenziale
U ( x, y, z )
determinata dalla legge di forza
per Forze Conservative l’energia totale è costante:
energia totale = K+U = cost
− esempi di forze conservative
• gravità; energia potenziale gravitazionale U(x)=mgx
• elastica; molla (legge di Hooke): U(x)=kx2
• elettrica; energia potenziale elettrica U(x)=kq1q2/x
− esempi di forze non-conservative (dissipative)
• attrito
• moto viscoso (velocità limite)
Fisica II – CdL Chimica
Le forze elettriche sono conservative
• Consideriamo una particella carica che si
sposta attraverso una regione in presenza
di un campo elettrico statico:
+
• una carica negativa è attratta
verso la carica positiva fissa
• la carica negativa possiede più
energia potenziale e meno energia
cinetica lontano dalla carica fissa
positiva, e …
• più energia cinetica e meno energia
potenziale vicino la carica positiva
fissa.
• Tuttavia, l’energia totale si
conserva
• Introduciamo ora l’energia
potenziale elettrica ed il
potenziale elettrostatico ….
Fisica II – CdL Chimica
Potenziale Elettrico e Energia Potenziale
• Immaginiamo una carica di prova, Qo, in un campo elettrico
esterno, E(x,y,z) (Ciascuna componente Ex Ey Ez è una
funzione di x,y,z)
• Qual’è l’energia potenziale, U(x,y,z) della carica in questo
campo?
– Definiamo arbitrariamente dove U(x,y,z) è nulla: a
distanza infinita (per distribuzioni di carica che sono
finite)
– U(x,y,z) è eguale al lavoro necessario per portare Qo
dal punto dove U è nulla al punto (x,y,z)
• Definiamo V(x,y,z) mediante U(x,y,z) = QoV(x,y,z)
• U dipende da Qo , ma V è independente da Qo (che può
essere + oppure -)
• V(x,y,z) è il potenziale elettrico associato con E(x,y,z)
–V(x,y,z) è un campo scalare
Fisica II – CdL Chimica
Potenziale Elettrico ...
• Supponiamo che la carica q0 si muova da A
a B attraverso una regione di spazio in cui
è presente il campo elettrico E.
q0
E
A
B
• Poichè sulla carica agirà una forza dovuta ad E, una
certa quantità di lavoro WAB dovrà essere fatto per
ottenere questo risultato.
• Definiamo la differenza di potenziale elettrico come:
WAB è la differenza
di energia potenziale
per andare da A a B
W
W
VB − VA ≡ A→ B ≡ AB
q0
q0
• È una buona definizione ?
• È VB - VA indipendente da
q0?
• È VB - VA indipendente dal cammino?
Fisica II – CdL Chimica
ΔV ha una intensità
ed un segno: +/Se - (VB più basso),
il lavoro svolto dal
campo è negativo,
mentre è positivo
quello svolto dalla
forza Fe
Unità di misura:
Volt=Joule/Coulomb
Indipendente dalla carica di prova ?
Per muovere una carica in un campo E,
dobbiamo applicare una forza eguale ed
opposta a quella cui è soggetta la carica
a causa della presenza del campo E.
B
∫
Fapplicata = -Felet
Felet
q0
E
A
B
B
∫
lavoro = forza × spostamento WAB = − Felet idl = − q0 E idl
⇒
B
WAB
VB − VA ≡
= − ∫ E idl
A
q0
A
A
Indipendente dalla carica.
• una carica positiva “cadrà” da un potenziale più alto ad uno più
basso guadagnando Energia Cinetica, ovvero un lavoro negativo
esterno viene svolto.
• per far andare una carica positiva di prova dal punto a potenziale
più basso a quello più alto è necessario “spendere” energia –
svolgere un lavoro esterno (ovvero la particella potrebbe perdere
energia cinetica)
Fisica II – CdL Chimica
Esempio 1
• una carica singola ( Q = -1μC) è fissa
all’origine. Definire un punto A a
x=+5m e un punto B a x = +2m.
B
– Qual’è il segno della differenza di potenziale -1μC
tra A e B? (VAB ≡ VB - VA )
(a) VAB < 0
(b) VAB = 0
×
A
×
x
(c) VAB > 0
•La maniera più semplice per ricavare il segno della differenza di potenziale è
di immaginare di porre una carica positiva nel punto A e determinare se un
lavoro positivo o negativo debba essere svolto nl muovere la carica al punto B.
•Una carica positiva in A sarebbe attratta verso la carica da -1μC; pertanto un
lavoro esterno NEGATIVO dovrebbe essere svolto per muovere la carica da A
a B. (si noti, il campo E esegue un lavoro positivo su questa carica positiva)
•Si può anche determinare il segno direttamente dalla definizione:
Poichè
VAB <0 !!
Fisica II – CdL Chimica
,
Indipendente dal Cammino ?
B
W AB
VB − V A ≡
= −∫ E ⋅ d
q0
A
Felet
-Felet
q0
E
A
• Definizione della differenza di potenziale :
ΔVAB=VB - VA.
B
dl
• L’integrale è la somma delle componenti tangenziali
(al cammino) del campo elettrico lungo il percorso
da A a B.
• La questione è: Dipende questo integrale dallo
specifico percorso scelto per andare da A a B ?
Fisica II – CdL Chimica
Vediamo se è veramente indipendente
• Consideriamo il caso di un campo costante: B
– via diretta: A - B
h
B
VB − VA = − ∫ E idl = Eh
A
Notare che dℓ
punta in verso
opposto a E.
dℓ
A
θ
r
C
E
dℓ
– via più lunga: A - C – B
C
B
C
A
C
A
VB − VA = − ∫ E idl − ∫ E idl = − ∫
( −E d
sin θ ) − 0 = E sin θ r = Eh
ricordare cos ( 90 + θ ) = − sin θ
Abbiamo almeno un esempio di un caso in cui l’integrale è
lo stesso per ENTRAMBI i cammini.
Fisica II – CdL Chimica
Lavoro e differenza (') di Energia Potenziale
Gravità
W = F d cos(T)
• mattone spostato yi→ yf
• FG = mg (giù)
• WG = -mgh
• 'UG= +mgh
y f→
Fg=mg
Fg=mg
h
Fg=mg
Fg=mg
Fg=mg
Fg=mg
y i→
Fg=mg
Fg=mg
Fisica II – CdL Chimica
Elettrico
• carica spostata ∞ → rf
• FE = kq1q2/r2 (sinistra)
• WE = -kq1q2/rf
• 'UE= +kq1q2/rf
rf
1. Lavoro da eseguire per
avvicinare 3 cariche
(da +1, +2 e +3 μC rispettivamente)
• W1 = 0
• W2 = k q1 q2 /r
=(9×109)(1×10-6)(2×10-6)/5
=3.6 mJ
• W3 = k q1 q3/r + k q2 q3/r
(9×109)(1×10-6)(3×10-6)/5 + (9×109)(2×10-6)(3×10-6)/5 =16.2
•
•
•
Wtotale = +19.8 mJ
WE = -19.8 mJ
ΔEen.pot.elettrica = +19.8 mJ
(occhio ai segni!)
Fisica II – CdL Chimica
5m
1
3
5m
5m
2
mJ
2. Lavoro da eseguire per
avvicinare 3 cariche negative
(da -1, -2 e -3 μC rispettivamente)
Quanto lavoro ci costerà avvicinare 3 cariche negative ?
cariche simili si respingono, quindi
dovremo ancora eseguire un lavoro
positivo !
a) W = +19.8 mJ
b) W = 0 mJ
c) W = -19.8 mJ
Fisica II – CdL Chimica
5m
1
3
5m
5m
2
1
5m
3. Lavoro necessario per
avvicinare 3 cariche
(uguali in valore assoluto)
2
+
+
5m
5m
-
3
Il lavoro totale da eseguire (da parte vostra,
cioè dello sperimentatore) per mettere
insieme queste cariche è:
a)
positivo
portare (1): lavoro nullo
b)
nullo
portare (2): lavoro positivo
negativo
portare (3): lavoro negativo x 2
c)
Fisica II – CdL Chimica
Potenziale Elettrico
• Unità Joules/Coulomb ≡Volts
– Batterie
– Prese elettriche
– Celle fotovoltaiche
– Dinamo
• In realtà sono differenze di potenziale
• Linee Equipotenziali (equilivello)
• Le linee del campo puntano verso il basso
• a distanza r dalla carica q, avendo scelto
in particolare V(∞) = 0
Fisica II – CdL Chimica
q
V =k
r
Potenziale Elettrico: carica puntiforme
• Abbiamo considerato finora differenze di potenziale.
B
VAB ≡ VB − VA = − ∫ E idl
• Definiamo il potenziale elettrico di un punto nello spazio come la A
differenza di potenziale tra quel punto e un punto di riferimento.
• un buon punto di riferimento è l’infinito ... tipicamente si pone V∞=0
• quindi il potenziale elettrico è definito come:
V ( r ) ≡ Vr − V∞
per una carica puntiforme all’origine, integriamo dall’infinito lungo un
certo asse, p.es. l’asse x
• “r” è la distanza dall’origine
integrale
di linea
r
V ( r ) − V ( ∞ ) = − ∫ E i dl
∞
VAB
1
r
r
⇒ V = − ∫ Edr '
∞
r
q
q
1
q
′
′
=
−
=
−
V =−
dr
dr
4πε 0 ∞∫ r '2
4πε 0 ∞∫ r '2
4πε 0
dl
V (r ) ≡ V (r ) −V (∞) =
Fisica II – CdL Chimica
1 q
4πε 0 r
1
q
essendo E =
4πε 0 r '2
r
1 q
⎡ 1⎤
−
=
⎢⎣ r ' ⎥⎦
4πε 0 r
∞
Energia Potenziale Elettrica vs.
Potenziale Elettrico
• Energia Potenziale Elettrica (U) – l’energia di
una carica in un punto.
• Potenziale Elettrico (V) - proprietà di un punto
nello spazio – ci dice quale EPE avrebbe una
carica q se fosse posta in quel punto
(generalmente ci riferiamo a differenze di
potenziale tra due punti):
U = Vq
• Ciascuna delle due quantità è funzione solo del
posto (scalare). Il segno è importante !
Fisica II – CdL Chimica
Potenziale Elettrico
• Dati tre punti A, B, C in
un campo E uniforme
C
E uniforme →
A
B
Come è il potenziale elettrico nel punto A rispetto al punto B ?
1) maggiore
2) eguale
3) minore
Fisica II – CdL Chimica
Il campo elettrico va da A a B
Il campo è uniforme così il potenziale elettrico
è eguale in tutti i punti
Il potenziale elettrico in A è minore del
potenziale in B perchè il punto C interferisce
con il massimo del potenziale in A.
Potenziale Elettrico
• Dati tre punti, A e B
all’interno di un conduttore
e C all’esterno, immersi in
un campo E uniforme
C
E uniforme →
A
conduttore
B
Il potenziale elettrico nel punto A è __???__ che nel punto B
1) maggiore
2) eguale
3) minore
Fisica II – CdL Chimica
“perchè il campo elettrico è nullo in ogni
punto all’interno di un materiale
conduttore”
Potenziale Elettrico
+
Ε
C
A
B
Il potenziale elettrico (generato dall’unica carica positiva)
nel punto A è __???__ che nel punto B
1) maggiore
• Le linee del campo elettrico puntano “verso il
basso”
2) eguale
• La linea AC è equipotenziale (perpendicolare ad E)
3) minore
• La linea CB è “verso il basso”, così B è ad un
Fisica II – CdL Chimica
potenziale più basso di A
Potenziale Elettrico generato da
un Protone
Qual’è il potenziale elettrico ad una distanza
r=0.53×10-10m da un protone ? (Sia V(∞)=0)
V =U/q= k q/ r =(9×109C2N-1m-2)(1.6×10-19C) /0.53×10-10m=
27.2 volts
rf = 0.5×10-10 m
+
Fisica II – CdL Chimica
Potenziale dovuto ad un insieme di N cariche puntiformi
Il potenziale da un insieme di N cariche è
proprio la somma algebrica del potenziale
dovuto a ciascuna carica separatamente.
q1
DI NUOVO IL PRINCIPIO DI
SOVRAPPOSIZIONE.
q2
V (r ) = −
r =r
∫
r =∞
⇒
NN
E idl = −
r =r N
r1
x
r2
r3
q3
i
E
dl
∑
∫
r =∞ n =1
NN
qqnn
V ( r ) = ∑ Vnn ( rr) ==
∑
44πε 00 nn==11 rrnn
nn==11
11
In generale per un sistema di N cariche puntiformi, il
potenziale in un punto a distanza ri da ciascuna carica vale:
Fisica II – CdL Chimica
Due Cariche
•Calcolare il potenziale elettrico nel punto A dovuto
alle cariche presenti
–Calcolare V dalla carica +7μC
–Calcolare V dalla carica –3.5μC
–Sommarli
•V = kq/r
V7=(9×109C2N-1m-2)(7×10-6C)/5m = 12.6×103V
V3=(9×109C2N-1m-2)(-3.5×10-6C)/5m = -6.3×103V
4m
A
Vtot = V7+V3 = +6.3×103V
Q=+7.0μC
Quanto lavoro bisogna spendere per portare
una carica da 2 μC dall’infinito al punto A?
Fisica II – CdL Chimica
6m
Q=-3.5 μC
W=ΔU=ΔVq
=(+6.3×103V)(2μC)
=+12.6 mJ
Due Cariche
• Nella regione II (tra le due cariche) il
potenziale elettrico è :
1) sempre positivo
2) positivo in alcuni punti, negativo in altri.
3) sempre negativo
Ι
ΙΙ
Q=+7.0μC
ΙΙΙ
Q=-3.5 μC
Molto vicino alla carica positiva il potenziale è positivo
Molto vicino alla carica negativa il potenziale è negativo
Fisica II – CdL Chimica
• Quale delle seguenti distribuzioni di carica produce V(x)= 0
per tutti i punti sull’asse delle x ? (si definisca V(x) ≡ 0 per
x=∞)
+2μC
+1μC
+2μC
+1μC
x
-1μC
-2μC
(a)
+2μC
-2μC
x
-1μC
-2μC
(b)
x
-1μC
(c)
+1μC
La soluzione consiste nel rendersi conto che per calcolare il potenziale
totale in un punto, dobbiamo solo eseguire una somma ALGEBRICA dei
contributi individuali
Pertanto, per avere V(x)=0 per tutte le x, dobbiamo avere che i contributi +Q
e -Q si annullino a vicenda, il che significa che qualunque punto sull’asse x
deve essere equidistante da +2μC e -2μC ed anche da +1μC e -1μC.
Questa condizione è rispettata solo nel caso (a)!
Fisica II – CdL Chimica
Potenziale dovuto a un dipolo elettrico
1 ⎛ q −q ⎞
VP =
⎜ −
⎟
4πε 0 ⎝ r+ r− ⎠
Se il punto P è abbastanza distante
sarà r>>d e quindi
r− − r+ ≈ d cos θ
e
r− × r+ ≈ r 2
qd cos θ
1 p cos θ
VP =
=
2
4πε 0
4πε 0 r 2
r
1
Il potenziale presenta una simmetria cilindrica lungo l’asse z e varia come
1/r2, diversamente da quello di una carica puntiforme 1/r.
Si noti che per θ=90° si ha V=0 (nello spostare una carica nel piano xy il
dipolo non compie lavoro).
Si osservi che sul piano xy V=0 ma ciò non implica che E=0 !
Fisica II – CdL Chimica
Potenziale Elettrico
Curve Equipotenziali ed Energia
U = qV
Fisica II – CdL Chimica
Superfici Equipotenziali
Definizione: Il luogo dei punti con lo stesso potenziale.
•
Esempio: per una carica puntiforme, le superfici equipotenziali sono
sfere centrate sulla carica.
• PROPRIETA’ GENERALE :
– Il campo elettrico è sempre perpendicolare ad una superficie
equipotenziale.
B
VB − VA = − ∫ E idl
• Perchè ?
A
Sulla superficie, NON vi è variazione di
Pertanto,
V
(perchè è equipotenziale!)
B
− ∫ E • dl = Δ V = 0
A
Si può concludere allora, che E • dl
è nullo.
Se il prodotto scalare tra il campo vettoriale ed il vettore
spostamento è nullo, quindi i due vettori sono perpendicolari, ovvero il
campo elettrico è sempre perpendicolare alla superficie equipotenziale.
Fisica II – CdL Chimica
Superfici Equipotenziali di una sfera carica
Er
Superfici
Equipotenziali
• Il campo elettrico della sfera carica ha una simmetria sferica.
• Il potenziale dipende solo dalla distanza dal centro della sfera,
come ci si aspetta dalla simmetria sferica.
• Pertanto, il potenziale è costante su una sfera concentrica alla
carica puntiforme. Queste superfici sono dette “equipotenziali”.
• Notare che il campo elettrico è perpendicolare alla superficie
equipotenziale in tutti i punti.
Fisica II – CdL Chimica
Potenziale di una sfera
uniformemente carica
Esercizio
Una sfera isolante di raggio R ha una densità di carica
positiva ed uniforme con una carica totale Q.
Determinare il potenziale elettrico: (a) all’esterno e (b)
all’interno della sfera.
Fisica II – CdL Chimica
Potenziale di una sfera
uniformemente carica
Per il teorema di Gauss, al di fuori di
Q
Er = ke 2
( per r > R )
una sfera uniformemente carica
r
diretto radialmente verso l’esterno essendo Q positiva. Per
ottenere il potenziale nel punto B
dr
Q
VB = − ∫ Er dr = −keQ ∫ 2 =ke
∞
∞ r
r
r
r
( per r > R ≡ carica
puntiforme )
Per il teorema di Gauss, all’interno di una sfera uniformemente carica
(
qin = ρV ′ = ρ 4 π r 3
3
⇒ Er =
qin
4πε 0 r
2
Fisica II – CdL Chimica
=
)
2
4
π
=
EdA
E
r
(
)=
∫
e
(
ρ 43 π r3
4πε 0 r
2
)=
qin
ε0
4 π R3
Q
Q
ρ
3
r=
r = ke 3 r
R
3ε 0
3ε 0
( per r < R )
Potenziale di una sfera
uniformemente carica
D
Dalla relazione ΔV = − ∫ E ids
C
ke Q r
ke Q 2 2
VD − VC = − ∫ Er dr = − 3 ∫ r dr =
R −r )
(
3
R
R R
2R
Q
per continuità deve essere, VC = ke
( per r = R )
R
2
⎛
ke Q
r ⎞
3− 2 ⎟
sostituendo VC si ha VD =
( per r < R )
3 ⎜
2R ⎝
R ⎠
r
Fisica II – CdL Chimica
Potenziale di una sfera uniformemente carica
Fisica II – CdL Chimica
Potenziale di un guscio sferico
conduttore carico
V
• Campo E (Legge di Gauss)
•
•
Q
4πε0 a
r < a: Er = 0
Er =
r >a:
Q
4πε0 r
a
1
Q
4πε 0 r 2
r
a
• Potenziale
a
• r > a:
r =r
V (r ) = −
∫
r =r
E idl = −
r =∞
• r < a:
V (r ) = −
∫
Er dr =
r =∞
1 Q
4πε 0 r
E=0, quindi nessun ulteriore cambiamento in V fino a V(a)
r =r
∫
r =∞
Fisica II – CdL Chimica
r
a
r
∞
∞
a
E idl = − ∫ Er dr = − ∫ Er dr − ∫ Er dr =
1 Q
+0
4πε 0 a
Cosa significa questo risultato ?
• Grafico della componente radiale del campo elettrico di
Er
un guscio sferico carico:
Notare che dentro il guscio, il campo
elettrico è nullo. Fuori dal guscio, il
campo elettrico diminuisce come 1/r2.
a R
r
V
Il potenziale per r>a è dato
4πε0 a
dall’integrale di Er.
Questo integrale è semplicemente l’area
sotto la curva Er .
Q
Q
4πε0 r
a R
a
a
Fisica II – CdL Chimica
r
In definitiva ...
• Se conosciamo il campo elettrico
E,
B
VB − VA = − ∫ E idl
A
questa relazione permette di calcolare il potenziale V
ovunque (noto per definizione VA , p.es. VA = 0 )
N
•
N
qn
Potenziale dovuto ad n cariche: V ( r ) = ∑ Vn ( r ) =
∑
4πε 0 n =1 rn
n =1
1
• Le superfici equipotenziali sono superfici su cui il
potenziale è costante.
Fisica II – CdL Chimica
Conduttori
B
VB − VA = −∫ E ⋅ ds
A
Tesi
+
+
+
+
+
+
+
+
+
+
+
+
+
+
La superficie di un conduttore è sempre una superficie
equipotenziale (infatti, l’intero conduttore è
equipotenziale)
Perchè ?
Se la superficie non fosse equipotenziale, ci sarebbe una
componente del campo elettrico parallela alla superficie e le
cariche si muoverebbero di conseguenza !! Similarmente a quanto
avviene all’interno del conduttore.
Il campo elettrico è perpendicolare alla superficie equipotenziale in
tutti i punti lungo la superficie stessa, altrimenti, le cariche
all’interno si muoverebbero. Pertanto, spostandoci lungo la
superficie, il potenziale non cambia.
Fisica II – CdL Chimica
Carica sui Conduttori
• Come è distribuita la carica sulla superficie di un
conduttore ?
– Deve produrre
superficie.
E=0
dentro il conduttore e
esempio Sferico
+ +
+
- -- +
- +
+ -+q - +
+ - +
+ - +
+
+ + +
+
Fisica II – CdL Chimica
E
normale alla
(con piccola carica fuori-centro):
E=0
dentro il guscio conduttore.
la densità di carica indotta sulla
superficie interna è non-uniforme.
la densità di carica indotta sulla
superficie esterna è uniforme
E
esterno ha una simmetria sferica
rispetto al centro del guscio sferico
conduttore.
Carica sui Conduttori
• Come è distribuita la carica su un conduttore non-sferico ?
• Evidenza: la densità di carica è maggiore nelle zone con il più
piccolo raggio di curvatura.
piccola σ
grande σ
r
• 2 sfere, connesse da un filo e “distanti”
• Entrambe allo stesso potenziale
Inoltre
σS
=
σL
Fisica II – CdL Chimica
rS
QS
L
QS rS
=
⇒
=
4πε 0 rS 4πε 0 rL
QL rL
QL
La sfera più piccola
QS 4πε r
σ S rL ha la densità di
⇒
=
superficiale
QL 4πε r
σ L rS carica
maggiore !
Sulla superficie di un conduttore aguzzo il campo
elettrico può essere abbastanza intenso da ionizzare le
molecole dell’aria (scarica per effetto corona).
2
0 S
2
0 L
Superficie Equipotenziale (Esempio)
• Le linee del del campo sono
più “fitte” in prossimità delle
zone con grande curvatura.
• Le linee del campo sono A
alla superficie in prossimità
della stessa (poichè la
superficie è equipotenziale).
• Le linee equipotenziali hanno
forma simile a quella della
superficie (in prossimità della
stessa).
• Le linee equipotenziali sono
simili ad un cerchio (sfera in
3-D) per grandi r.
Fisica II – CdL Chimica
piccola σ
grande σ
piccolo E
grande E
σ
E=
ε0
Sfera conduttrice
z Il massimo potenziale su un conduttore è limitato dal
fatto che l’aria circostante diventa conduttrice se
Emax = 3 × 10 V / m
6
1 q
essendo E =
4πε0 r 2
z R=1 cm
z R=1m
V max
1 q
V=
4πε0 r
V=ER
V
−2
4
= 3 × 10
× 10 m = 3 × 10 V
m
V max = 3 × 10
Fisica II – CdL Chimica
→
6
6
V
× 1 m = 3 × 10 6 V
m
Calcolo di E da V
• Possiamo ottenere il campo elettrico E dal potenziale
invertendo la precedente relazione tra E e V:
V
B
VB − VA = − ∫ E ⋅ d s
A
∂V
Ex = −
∂x
r
V
∂V
Ey = −
∂y
r + xˆ dx
V+dV
∂V
Ez = −
∂z
ˆ = − Ex dx
dV = − E ⋅ xdx
• Espresso come un vettore,E è il gradiente negativo di
Fisica II – CdL Chimica
E = −∇ V
V
Calcolo di E da V
Che cosa significa che E è il gradiente
negativo di V ?
E = −∇ V ovvero E = −gradV
• coordinate cartesiane :
∇V =
• coordinate sferiche : ∇ V =
∂V
∂V
∂V
xˆ +
yˆ +
zˆ
∂x
∂y
∂z
∂V
1 ∂V ˆ
1 ∂V
θ+
ϕˆ
rˆ +
∂r
r ∂θ
r sin θ ∂ϕ
• a parole:
– la direzione della più “rapida diminuzione” di V, (massima
pendenza), è la direzione del campo E in quel punto, e
l’intensità (modulo) di E è esattamente la pendenza.
• Analogia con la gravità:
– Consideriamo il caso di un “paesaggio” (valli e monti)-- una palla accelera
verso il basso, e la componente della forza gravitazionale che agisce sulla
palla è il “gradiente” lungo il “terreno scosceso”. La palla inizia a muoversi
lungo la direzione della maggiore pendenza.
– Lasciando la palla il gradiente 3-D del potenziale gravitazionale punta verso
il centro della Terra, ed è la forza dovuta alla gravità.
Fisica II – CdL Chimica
Calcolo di E da V: linee equipotenziali
Le linee tratteggiate rappresentano i luoghi (geometrici)
equipotenziali (V=cos.)
Fisica II – CdL Chimica
Calcolo di E da V: dipolo elettrico
Si calcoli il campo elettrico in P.
Essendo
12
z
2
2
r = ( x + z ) e cos θ =
12
2
2
(x + z )
Da un problema precedente:
1 p cos θ e sostituendo
VP =
4πε 0 r 2
VP =
p
z
(
4πε 0 x 2 + z 2
∂V
p
=−
Ez = −
∂z
4πε 0
Fisica II – CdL Chimica
)
(x
Dalla relazione E = −∇ V si ha
32
2
+z
2
)
32
⎡3 2
− z ⎢ x + z2
⎣2
(
(x
2
+z
2
)
3
) ⎤⎥⎦ ( 2 z )
12
=−
x2 − 2z 2
p
(
4πε 0 x 2 + z 2
)
52
Calcolo di E da V: dipolo elettrico
Sull’asse del dipolo (x=0)
1 2p
Ez =
4πε 0 z 3
in accordo con precedenti
risultati, mentre lungo l’asse z
Ex=0 per simmetria.
Sul piano mediano del dipolo (z=0)
per punti lontani:
p Anche questo in accordo con quanto già ricavato,
Ez = −
4πε 0 x3 con maggiore difficoltà, dalla legge di forza.
1
Svolgere delle derivate è certamente più semplice che
combinare i contributi della varie cariche al campo elettrico !
Fisica II – CdL Chimica
Calcolo di E da V: Esempio
• Consideriamo il seguente potenziale elettrico:
V ( x, y, z ) = 3 x + 2 xy − z
2
2
• Quale campo elettrico descrive ?
∂V
Ex = −
= −6 x − 2 y
∂x
... esprimendolo
come un vettore:
si ha:
Fisica II – CdL Chimica
∂V
∂V
Ey = −
= −2 x Ez = −
= 2z
∂y
∂z
∂V
∂V
∂V
∇V =
xˆ +
yˆ +
zˆ
∂x
∂y
∂z
E ( x , y , z ) = ( −6 x −2 y ) xˆ − 2 x yˆ + 2 z zˆ
In definitiva ...
Se conosciamo il campo
WAB
VB − VA ≡
q0
Á
E ovunque,
B
VB − VA = − ∫ E • dl
A
possiamo calcolare la funzione potenziale V ovunque (si
rammenti, che spesso definiamo VA = 0 in qualche punto (∞))
Se conosciamo la funzione potenziale
V ovunque,
E = −∇ V
possiamo calcolare il campo elettrico
E
ovunque
• Unità di misura del Potenziale V = J/C
• Unità di misura del Campo Elettrico V/m
Fisica II – CdL Chimica