Prova Scritta di Fisica
Corso di Studi in Ingegneria Civile, Università della Calabria, 1 Luglio 2014
Esercizio 1: Una molla ideale è utilizzata per frenare un blocco di massa 50 kg che striscia su un
piano orizzontale di coefficiente di attrito dinamico
µd = 0.5 e coefficiente di attrito statico µs = 0.75.
Quando il blocco si trova a 80 cm dalla molla, la sua
velocità è pari a 4.5 m/s. Sapendo che la frenata
produce una compressione di 8 cm, determinare il
valore della costante elastica k. Quale valore massimo della costante elastica kmax permetterebbe al blocco di rimanere fermo dopo la frenata?
In un successivo esperimento, la molla in questione ha una costante elastica k = 2kmax ,
calcolare lo spazio percorso dal blocco dopo aver compresso la molla prima di fermarsi.
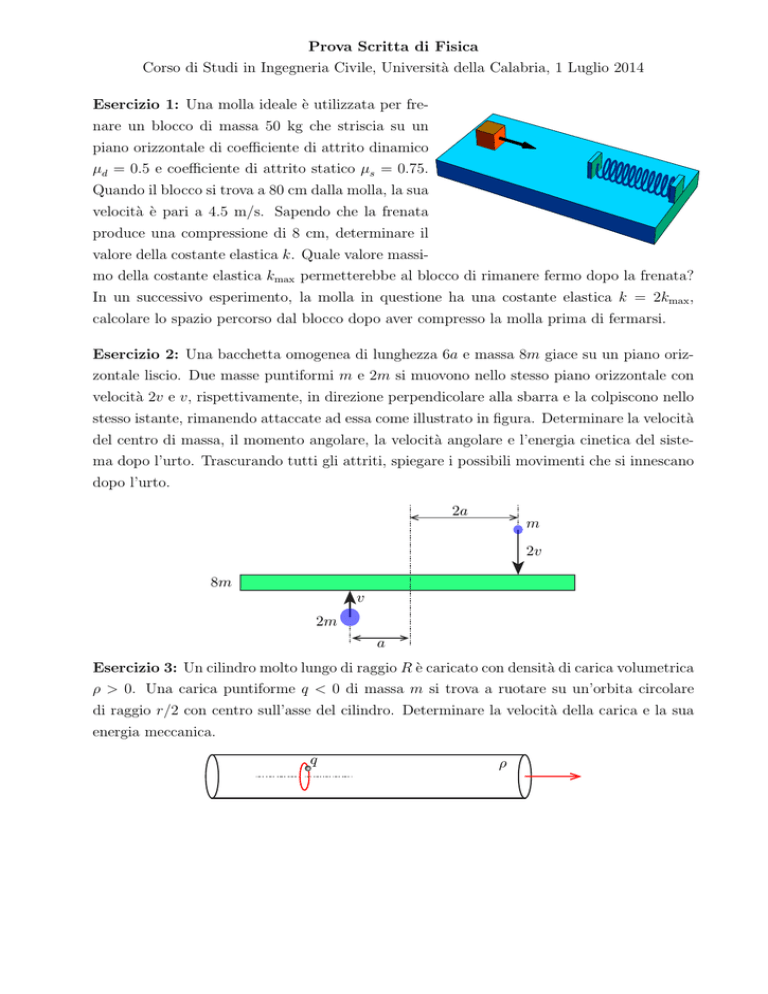
Esercizio 2: Una bacchetta omogenea di lunghezza 6a e massa 8m giace su un piano orizzontale liscio. Due masse puntiformi m e 2m si muovono nello stesso piano orizzontale con
velocità 2v e v, rispettivamente, in direzione perpendicolare alla sbarra e la colpiscono nello
stesso istante, rimanendo attaccate ad essa come illustrato in figura. Determinare la velocità
del centro di massa, il momento angolare, la velocità angolare e l’energia cinetica del sistema dopo l’urto. Trascurando tutti gli attriti, spiegare i possibili movimenti che si innescano
dopo l’urto.
2a
m
2v
8m
v
2m
a
Esercizio 3: Un cilindro molto lungo di raggio R è caricato con densità di carica volumetrica
ρ > 0. Una carica puntiforme q < 0 di massa m si trova a ruotare su un’orbita circolare
di raggio r/2 con centro sull’asse del cilindro. Determinare la velocità della carica e la sua
energia meccanica.
q
ρ
Soluzione 1:
Nel primo esperimento il blocco parte da una distanza d = 0.80 m, con velocità v0 =
4.50 m/s, e striscia sul piano orizzontale fino a comprimere la molla (di un tratto δ = 0.08 m).
Nel processo la sua variazione di energia meccanica
1
1
∆Em = kδ 2 − mv02
2
2
è pari al lavoro prodotto dalla forza di attrito dinamico
L = −µd mg (d + δ) .
Ne segue
1 2 1 2
kδ − mv0 = −µd mg (d + δ)
2
2
da cui
k=−
2dgµd m 2gµd m mv02
−
+ 2 = 90828.1 N/m.
δ
δ2
δ
La velocità del blocco nel punto di massima compressione è nulla. Se la costante elastica
avesse un valore inferiore a kmax tale da rendere la forza elastica completamente bilanciata
dalla forza di attrito statico,
kmax δ − µs mg = 0 ⇒ kmax =
µs mg
= 4593.75 N/m,
δ
il corpo rimarrebbe fermo con la molla compressa. Nel primo esperimento la costante elastica
consente alla molla di decomprimersi e al corpo di essere respinto.
Nel secondo esperimento la costante elastica della molla (k = 2kmax ) permette una compressione δ x maggiore di quella del primo esperimento. Infatti, procedendo come nella prima
parte del problema, si trova:
1
1
∆Em = L ⇒ kδ 2x − mv02 = −µd mg (d + δ x )
2
2
s
gmµd
⇒ δx =
k
!
kv02
2dk
+ 1 − 1 = 23.46 cm
−
g 2 mµ2d gmµd
Nella fase di decompressione la molla è frenata dalla forza di attrito dinamico. Il nuovo
punto di equilibrio x0 è dato dal punto di annullamento della forza elastica e della forza di
attrito dinamico:
−kx0 − µd mg = 0 ⇒ x0 =
µd mg
= 2.67 cm.
k
2
La molla si porta in posizione x0 poggiando sul blocco con energia cinetica massima mvmax
/2,
e il blocco subisce una variazione di energia meccanica pari a
2
mvmax
kx20 kδ 2x
∆Em =
+
−
.
2
2
2
Nello stesso processo la forza di attrito dinamico compie il lavoro
L = −µd mg(δ x − x0 ),
per cui
2
mvmax
kx20 kδ 2x
+
−
= −µd mg(δ x − x0 ).
2
2
2
Nella fase successiva il blocco si stacca dalla molla con un’energia cinetica iniziale
2
k δ 2x − x20
mvmax
=
− µd mg(δ x − x0 ) = 198.574 J
2
2
e si ferma dopo aver percorso un tratto s tale che
2
2
mvmax
vmax
−
= −µd mgs ⇒ s =
= 81 cm
2
2µd g
Lo spostamento complessivo dal punto di massima compressione è dato da
s + δ x − x0 = 1.02 m.
Soluzione 2: La quantità di moto iniziale del sistema è nulla
P = 2mvj + m (−2vj) = 0,
dove con j si è indicato il versore della direzione perpendicolare alla bacchetta. Dopo l’urto
la quantità di moto totale riferita al centro di massa, che per simmetria rimane nel centro
della bacchetta, è data dall’espressione
P0 = (2m + m + 8m)Vcm .
Nell’urto si conserva la quantità di moto totale del sistema, per cui il centro di massa si
trova a riposo
P = P0 ⇒ 0 =11mVcm ⇒ Vcm = 0.
Il moto della bacchetta è puramente rotazionale intorno al centro di massa, rispetto all’asse perpendicolare al piano (z). In assenza di attriti la bacchetta ruota di moto circolare
uniforme, con un momento di inerzia
bacchetta
Icm,z = Icm,z
+ m (2a)2 + (2m) a2
8m
=
(6a)2 + m (2a)2 + (2m) a2 = 30ma2 .
12
Nell’urto si conserva anche il momento angolare. Con riferimento al centro di massa, si può
scrivere
Lcm = −6mavk = L0cm = Icm,z ωk = 30ma2 ωk,
da cui (rotazione in senso orario):
ω=
−v
.
5a
y
2a
m
2v
8m
CM
v
2m
a
Infine, l’energia cinetica del sistema è data dalla relazione
2
1
1
−v
3mv2
2
2
.
Ec = Icm,z ω = 30ma
=
2
2
5a
5
Soluzione 3: Il primo passo è la determinazione del campo elettrico nei punti della traiettoria percorsa dalla carica negativa. A tal fine si considera una superficie gaussiana Σ di
forma cilindrica, avente lo stesso asse della distribuzione di carica, un raggio pari a r/2, ed
un’altezza arbitraria l. Il campo elettrico della distribuzione è diretto perpendicolarmente
alla superficie Σ e in verso uscente. Il suo flusso, dato dal prodotto
r
ΦΣ (E) = 2π lE.
2
Per il teorema di Gauss esso equivale a q (Σ) /ε0 dove
q (Σ) = ρπ
r 2
2
l
rappresenta la carica interna alla superficie Σ. Ne segue:
r
ρπ r 2
ρr
2π lE =
l⇒E=
.
2
ε0 2
4ε0
y
2
r/
ρ
r/2
Σ
z
ur
O
E
q
x
In un sistema di coordinate cartesiano, con origine sul centro della traiettoria della carica,
e asse z parallelo all’asse della superficie Σ, il campo elettrico ha il verso della direzione
radiale del piano xy. La forza elettrica esercitata sulla carica è di natura centripeta
Fq = −
ρ |q| r
ur .
4ε0
Non essendo presenti forze tangenziali, l’accelerazione della carica è centripeta ed il moto
circolare uniforme
2
ma = Fq ⇒
2
mv
ρ |q| r
ρ |q| r
=
⇒ v2 =
⇒v=
r/2
4ε0
8mε0
s
ρ |q|
r.
8mε0
Equivalentemente, nel sistema di riferimento accelerato della carica si ha un equilibrio tra
la forza centripeta legata al campo elettrico e la forza centrifuga, di natura non inerziale.
Per associare un’energia meccanica alla carica, si può porre lo zero dell’energia potenziale
Ep nel centro della traiettoria circolare. Allora, Ep è data dal lavoro compiuto dalla forza
elettrica per spostare la carica da tale centro a un punto della circonferenza, distante r/2
dal centro:
r0 =0
ρ |q| r02 ρ |q| r2
Ep =
Fq dr = −
.
=
4ε0 2 r0 =r/2
32ε0
r/2
Z
0
0
Infine l’energia meccanica è pari a
Em =
3ρ |q| r2
ρ |q| r2 ρ |q| r2
+
=
16ε0
32ε0
32ε0












