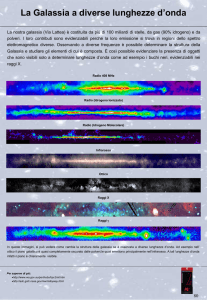
Cinematica di gas e stelle in galassie
Corso Astrofisica Gererale Mod.B - A.A. 2008-2009
Alessandro Pizzella
Dipartimento di Astronomia
Università di Padova
Novembre 2008 v3.5
1
Contents
1 Introduzione
3
2 Cenni di spettroscopia mono e bi-dimensionale
2.1 Spettroscopia a fenditura lunga (monodimensionale) . . . . . . . . . . . . . . . .
2.2 Unità a campo integrale (bidimensionale) . . . . . . . . . . . . . . . . . . . . . .
2.3 Cenni sulle misure di cinematica con HI . . . . . . . . . . . . . . . . . . . . . .
4
4
5
7
3 Misura della cinematica della componente gassosa
3.1 Misura del redshift . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Trasformare z in velocità . . . . . . . . . . . . . . . . . . . . . . .
3.3 Determinazione della velocità di sistema e del centro della galassia
3.4 Correzioni della velocità di sistema . . . . . . . . . . . . . . . . .
3.5 Distanza e scala della galassia . . . . . . . . . . . . . . . . . . . .
3.6 Deproiezione e passaggio a grandezze fisiche . . . . . . . . . . . .
3.6.1 Proiezione del campo di velocità di un moto rigido . . . .
3.6.2 Proiezione del campo di velocità V=costante . . . . . . . .
3.6.3 Campi di velocità reali . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Effetti strumentali e osservativi che influenzano le misure cinematiche
4.1 Convoluzione per Point Spread Function . . . . . . . . . . . . . . . . . . .
4.1.1 Metodo approssimato: convoluzione del campo di velocità . . . . .
4.1.2 Convoluzione del cubo di dati . . . . . . . . . . . . . . . . . . . . .
4.2 Fenditura grande rispetto alla galassia. . . . . . . . . . . . . . . . . . . . .
5 Misura della cinematica della componente stellare
5.1 Effetto del redshift sullo spettro . . . . . . . . . . .
5.2 Definizione di LOSVD . . . . . . . . . . . . . . . .
5.3 Spettro delle galassia come convoluzione . . . . . .
5.4 Determinazione della LOSVD . . . . . . . . . . . .
5.5 Fourier Quotient . . . . . . . . . . . . . . . . . . .
5.6 Momenti di ordine superiore: h3 ed h4 . . . . . . .
5.7 Esempi di campi di velocità mono e bidimensionali
A
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
17
19
21
21
22
23
24
24
25
.
.
.
.
26
26
27
28
30
.
.
.
.
.
.
.
33
33
34
34
36
37
37
38
42
A.1 Costanti utili . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
A.2 Formule utili . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
A.3 Distanze per z 6≪ 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2
Chapter 1
Introduzione
Lo studio della cinematica di una galassia si basa essenzialmente sull’analisi spettroscopica della
sua luce. In questa dispensa vengono illustrate le principali tecniche osservative utilizzate per
derivare la cinematica del gas ionizzato e della componente stellare. Viene inoltre illustrato,
ma in minor dettaglio, la misura della cinematica dell’idrogeno neutro.
Ricordiamo velocemente in questa introduzione quale è il fine scientifico della misura della
cinematica delle galassie. Senza dubbio lo scopo principale è lo studio della distribuzione
della massa. La cinematica di una galassia è determinata dalla somma dei contributi di tutte
le componenti, luminose e non, che contribuiscono alla massa di una galassia. Non mancano poi
ulteriori applicazioni. È possibile individuare componenti disaccoppiate cinematicamente.
La loro presenza è generalmente dovuta ad episodi di acquisizione nella storia evolutiva di una
galassia. La conoscenza della cinematica stellare è poi l’unico modo si ha per poter determinare
la funzione di distribuzione. Questa è legata alla storia di formazione della galassia. Diversi
scenari di formazione (clustering gerarchico, collasso monolitico) prevedono una diversa forma
della funzione di distribuzione.
3
Chapter 2
Cenni di spettroscopia mono e
bi-dimensionale
In questo capitolo vengono illustrate le principali tecniche utilizzate per ottenere informazioni
spettroscopiche mono e bi dimensionali. Quanto illustrato nei paragrafi 2.1 e 2.2 si applica tanto
a misure di cinematica della componente gassosa che della componente stellare. Nel paragrafo
2.3 tratteremo invece il caso di osservazioni radio della componente di gas neutro HI.
2.1
Spettroscopia a fenditura lunga (monodimensionale)
La tecnica osservativa maggiormente utilizzata in passato (e presente) per misure di cinematica di galassie è la spettroscopia a fenditura lunga (long slit spectroscopy). Uno spettroscopio tradizionale è infatti costituito da una fenditura, un collimatore, un elemento dispersore
(prisma, reticolo di diffrazione, grism) ed una camera CCD (Fig.2.3). La fenditura (slit in inglese) è posta nel piano focale ed è orientata perpendicolarmente alla direzione lungo cui verrà
dispersa la luce. Agisce di fatto come una maschera che blocca tutta la luce tranne una sottile
striscia. Questa striscia di luce è quella che entra nello spettroscopio e che verrà analizzata.
Dopo essere passata per il collimatore (che ha la funzione di rendere il fascio di luce parallelo)
l’elemento dispersore ”allarga” la luce deviando i vari fotoni con angoli che dipendono dalla
loro lunghezza d’onda. A questo punto la striscia di luce è diventata una immagine che viene
focalizzata e registrata dalla camera CCD. Essendo la fenditura orientata perpendicolarmente
alla direzione della dispersione, l’informazione spaziale (cioè ”dove” lungo la fenditura) e in
lunghezza d’onda non si mescolano. In pratica, se si immagina la fenditura come una serie di
piccole aperture contigue, lo spettro che si ottiene può essere visto come una serie di spettri
contigui ognuno relativo alla luce che passa attraverso una delle piccole aperture. Con spettri
a fenditura lunga posso quindi ottenere una informazione spettroscopica, e quindi cinematica, lungo un asse della galassia. Posso dire di avere una informazione monodimensionale.
(l’immagine CCD è bidimensionale ma una dimensione è la lunghezza d’onda) Generalmente si
orienta lo spettroscopio in modo da allineare la fenditura con l’asse maggiore della galassia in
esame, posizionandola sul centro di questa. (Nulla impedisce ovviamente di orientare la fenditura e posizionarla in altra maniera, su assi diversi dall’asse maggiore oppure lungo posizioni
non passanti per il centro della galassia). Nella figura 2.3 viene mostrato il tipico risultato
di uno spettro preso lungo l’asse maggiore di una galassia a disco. Nella figura 2.5 è stato
rimosso lo spettro del continuo stellare per meglio evidenziare le emissioni nelle regioni centrali.
Nella figura 2.6 è infine mostrato il profilo delle righe di emissione ad alcune posizioni lungo
la fenditura. Ogni posizione diversa sulla fenditura corrisponde ad una diversa posizione sulla
4
Figure 2.1: Schema ottico del funzionamento di uno spettrografo a fenditura lunga. Partendo
dall’altro verso il basso troviamo: piano focale con immagine della galassia; la fenditura che
lascia passare solo una striscia della luce della galassia; collimatore che rende i raggi paralleli;
grism che devia la luce a seconda della sua lunghezza d’onda (ogni lunghezza d’onda verrà
deviata di un determinato angolo); collimatore che focalizza lo spettro in uscita dal grism sul
CCD; il CCD
galassia.
2.2
Unità a campo integrale (bidimensionale)
Sono attualmente in fase di sviluppo strumenti che sono in grado di ottenere spettri non lungo
una fenditura ma su di un campo bidimensionale. Una classe di questo strumenti è quella
che utilizza la tecnica Fabbry-Perrot. Si tratta di un filtro interferenziale a banda stretta
(anche 1-2Å) tunabile. L’osservazione consiste nel prendere una serie di immagini della galassia
cambiando la lunghezza d’onda immagine dopo immagine. Ad esempio, volendo misurare
la cinematica della componente del gas ionizzato utilizzando la riga dell’Hα (λ6562.8Å) in
emissione, si regola il filtro a 6550Å (larghezza della banda passante 1Å) e si esegue la prima
integrazione. Si regola successivamente il filtro a 6551Å e si esegue la seconda esposizione, e
poi si prosegue fino a 6570Å. I maggiori ostacoli nell’utilizzo di questa tecnica sono:
1. il limitato intervallo in lunghezza d’onda ottenibile in un ragionevole tempo totale di
integrazione sull’oggetto. Ogni posa, data la piccola ampiezza in lunghezza d’onda del
filtro, deve durare diversi minuti.
2. la difficoltà di combinare assieme le immagini ottenute alle diverse lunghezze d’onda. Le
5
Figure 2.2: Spettro preso lungo l’asse maggiore di una galassia a spirale. L’immagine è orientata
in modo da avere la lunghezza d’onda lungo l’asse X e la posizione lungo la fenditura lungo
l’asse Y. Nella figura viene mostrata la regione spettrale che va da λ4700Åa λ5800Åmentre
l’estensione spaziale va da −70′′ a 70′′ (convenzionalmente indico come negative le posizioni che
nella figura sono al di sotto del centro della galassia e positive quelle al di sopra). Il centro della
galassia e’ in posizione centrale e il suo spettro appare come una riga orizzontale più intensa.
Sono visibili anche gli spettri di 2 stelle poste ai lati della galassia. Sono ben visibili le righe di
emissione Hβ4861.3Å,[OIII]λλ6958.9, 5006.8Å(vedi anche Fig.2.4). Le emissioni che percorrono
lo spettro verticalmente in tutta la sua estensione sono righe di emissione del cielo.
condizioni del cielo, la trasparenza e soprattuto il ”seeing” possono variare da una posa
all’altra e le immagini alle diverse lunghezze d’onda risultano quindi caratterizzate da una
differente risoluzione spaziale.
Uno dei principali vantaggi e’ invece l’ampio campo di vista, anche di alcuni minuti d’arco, che
è possibile ottenere.
Una classe di strumenti più moderna ed efficiente che sta subendo un rapido sviluppo è
quella delle unità a campo integrale (o IFU, integral field units). In questo caso il campo
viene diviso in una matrice rettangolare o quadrata di punti (con dimensioni che possono variare
indicativamente da 2” ×2” a 0.2” ×0.2”). Da ognuno di questi punti viene ottenuto uno spettro
con un normale spettroscopio. Mostriamo qui 2 esempio di come è possibile ottenere questo
utilizzando fibre ottiche (Fig.2.7) oppure una matrice di lenti (Fig.2.8). Nel primo caso la luce
viene portata sulla fenditura di uno spettroscopio tradizionale mediante delle fibre ottiche, nel
secondo caso si ottiene uno spettro senza fenditura ma dopo aver opportunamente indirizzato
la luce secondo una griglia opportunamente organizzata in modo che gli spettri relativi ad ogni
lente non si sovrappongano. In entrambi i casi il prodotto di una esposizione è allora una
6
Figure 2.3: Come al Fig.2.2 nell’intervallo spettrale che va da λ6430Å a λ6870Å mentre.
L’estensione spaziale va da −100′′ a 110′′ . Sono ben visibili le righe di emissione [NII]λ6548.0Å,
Hα6562.8Å,[NII]λ6583.4Å, [SII]λλ6716.4, 6730.8Å. L’emissione del cielo è stata sottratta.
immagine CCD (o più probabilmente un mosaico; VIMOS in uso presso il VLT (Cerro Paranal,
Cile, ESO) utilizza 4 CCD per registrare gli spettri) contenente molti spettri monodimensionali,
ognuno relativo ad una ben precisa posizione in cielo. Alternativamente è possibile utilizzare
degli ”image slicer” che letteralmente tagliano il campo in striscioline e le allineano lungo la
fenditura. Con questa seconda tecnica il prodotto di una esposizione è una serie di spettri
bidimensionali (Fig.2.9. I vantaggi dell’utilizzo di unità a campo integrale sono:
1. l’alta sensibilità;
2. l’alta risoluzione spettrale.
Una delle maggiori limitazioni è il limitato campo di vista. Ad esempio, una matrice di 40 × 40
punti produrrà 1600 spettri. Serve un CCD molto grande (tipicamente un mosaico di CCD)
per poter registrare tanta informazione.
Nella Fig.2.10 riassumiamo questi 3 tecniche principali di spettroscopia IFU con una semplice figura.
2.3
Cenni sulle misure di cinematica con HI
Un discorso a parte va invece fatto per quanto riguarda le osservazioni della componente di
gas neutro HI. Questo gas emette una riga di emissione alla lunghezza d’onda di 21cm. Si
tratta di una transizione proibita in qui l’atomo di idrogeno passa da uno stato in cui elettrone
e protone hanno spin parallelo (pi˘’ energetico) ad uno stato in cui gli spin sono antiparalleli
(minore energia). La differenza di energia fra questi due stati corrisponde alla lunghezza d’onda
7
Figure 2.4: Stesso spettro mostrato in Fig.2.2 dopo la sottrazione dell’emissione del cielo.
Oltre alle righe di emissione sono messe in evidenza le righe di assorbimento della banda del
Mg (queste sono visibili anche nello spettro delle 2 stelle).
di 21cm. Siamo nella banda radio e sono quindi necessari radiotelescopi per osservare questa
emissione. Le osservazioni radio sono eseguite con tecniche e strumenti molto diversi da quelli
ottici. Una proprietà molto utile a chi compie studi cinematici consiste nel fatto che è possibile
osservare contemporaneamente diverse lunghezze d’onda grazie ai diversi canali di cui è dotato
il radiotelescopio. Come tecnicamente questo sia possibile non è argomento di questa dispensa.
Il risultato pratico invece lo è. Di fatto si è in grado con un radiotelescopio di fare quello che fa
uno strumento Fabbry-Perrot (vedi par.2.2). In pratica possiamo misurare lo spettro attorno
alla riga 21cm nel piano del cielo ottenendo di fatto uno spettro bidimensionale. Da questi
dati si derivano facilmente campi di velocità bidimensionali cosı̀ utili per studi cinematici. Un
aspetto meno vantaggioso delle osservazioni radio è la limitata risoluzione spaziale. Non è
un problema di turbolenza atmosferica (che è il fattore limitante delle osservazioni ottiche da
terra) ma di dimensioni delle parabole. Il rapporto fra la lunghezza d’onda (21cm) e il diametro
della parabola non è cosı̀ piccolo come succede nelle osservazioni ottiche. Un radiotelescopio
a specchio unico può avere una risoluzione spaziale dell’ordine dei gradi! Per ovviare a questo
problema si utilizza la tecnica dell’interferometria. Si costruiscono più parabole distribuite su
un area molto estesa. Vi sono batterie di radiotelescopi lunghe diversi chilometri o addirittura
si accoppiano radiotelescopi posti in diversi continenti. In questo modo si riesce a migliorare
grandemente la risoluzione spaziale. Nel caso di oggetti brillanti si arriva a scale dell’ordine
dei milliarcsec. Per quanto riguarda le galassie e le osservazioni HI generalmente si riesce ad
ottenere una risoluzione spaziale dell’ordine di 20′′ − 30′′ . Per descrivere la risoluzione spaziale
di un radiotelescopio si indica in genere il beam. Questo è analogo a quello che è il seeing per
le osservazione ottiche ed è l’immagine con cui appare un oggetto puntiforme (ed è quindi una
misura della risoluzione spaziale, più il beam è piccolo e più posso risolvere oggetti vicini fra
8
Figure 2.5: Come la Fig.2.3 ma con il continuo stellare sottratto. Ora le righe di emissione
sono evidenti anche nella regione nucleare. Si riescono ad individuare anche alcune righe di
assorbimento. Ad esempio a sinistra di [NII]λ6548.0Å è presente una riga stellare inclinata a
causa della rotazione delle stelle. A destra di [SII]λ6730.8Å sono invece presenti delle righe di
assorbimento dovute all’atmosfera terrestre che appaiono dritte (λ costante lungo la fenditura).
loro)
Accenniamo infine alla tecnica detta single dish. In questo caso il radiotelescopio funziona
con una unica grande parabola e non è in grado di risolvere spazialmente la galassia avendo un
beam di diversi arcmin. Il risultato di una osservazione single dish di una galassia a spirale è un
profilo della riga a 21cm dalla quale si può misurare il redshift della galassia e si può ottenere
una buona stima della ampiezza della curva di rotazione.
9
Figure 2.6: Profili delle righe Hα e [NII]λλ6548.0, 6583.4Å ad alcune distanze dal centro della
galassia. Gli spettri sono stati spostati verticalmente per evitare che si sovrapponessero. Si può
notare come la lunghezza d’onda delle emissioni è diversa per raggi positivi e negativi a causa
della rotazione della galassia/.
10
Figure 2.7: IFU con fibre ottiche. Le fibre sono poste sul piano focale ed indirizzano la luce di
ogni celletta sulla fenditura di uno spettroscopio. Ogni fibra genererà uno spettro.
11
Figure 2.8: IFU con matrice di lenti. Le lenti dividono il piano focale in una matrice di punti
(in alto a sinistra). Ogni lente crea una immagine della luce (in alto a destra). In realtà la
matrice non è allineata con la direzione lungo cui viene dispersa la luce (in basso a sinistra).
In questo modo quando i piccoli fasci di luce vengono dispersi gli spettri non si sovrappongono
(in basso a destra).
12
Figure 2.9: IFU con image slicer. Opportuni elementi ottici sono in grado di dividere il piano focale (in basso a destra) letteralmente in strisce. La fenditura dello spettroscopio verrà
illuminata come indicato in alto a sinistra
13
Figure 2.10: Figura riassuntiva delle 3 principali tecniche di spettroscopia IFU: matrice di lenti,
fibre ottiche, image slicer.
14
Figure 2.11: Misure di HI. Le diverse immagini rappresentano l’emissione 21cm registrata dai
diversi canali. Si può notare come la lunghezza d’onda tende ad essere diversa dai due lati della
galassia a causa della rotazione del disco.
15
Figure 2.12: Osservazioni 21cm della galassia a spirale NGC 2403. Dal riquadro in alto a sinistra
troviamo in ordine: immagine in banda ottica (Digitalized Sky Survey); profilo di densità HI
(punti); mappa HI; campo di velocità; continuo radio; dispersione di velocità. Questi ultimi
4 sono stati ottenuti con un beam di 15′′ . Nel campo di velocità i livelli sono tracciati ogni
20 km/s. La linea più scura indica la velocità di sistema (133 km/s)
16
Chapter 3
Misura della cinematica della
componente gassosa
Una volta ottenuto lo spettro di un punto della galassia, sia esso un punto lungo la fenditura o
un punto della matrice bidimensionale di un IFU, vogliamo determinare la cinematica del gas.
I passi da seguire sono i seguenti:
1. determinare la lunghezza d’onda dell’emissione e quindi il redshift
2. trasformare il redshift in velocità
3. ”simmetrizzare” la curva di rotazione determinando l’esatta posizione del centro cinematico e la velocità radiale del centro cinematico della galassia
4. correggere la velocità della galassia per il moto della terra attorno al sole e per il moto
del sole rispetto al fondo cosmico
5. calcolare la distanza della galassia da noi e la scala (pc/arcsec)
6. deproiettare le grandezze osservate (velocità e distanze galattocentriche) per trasformarle
in unità fisiche.
3.1
Misura del redshift
Le righe di emissione del gas ionizzato sono generalmente caratterizzate da una bassa dispersione
di velocità (nella zona del disco σgas ≤ 20 km/s. Questo è dovuto alla natura dissipativa del
gas che lo costringe e muoversi in orbite circolari. La formula dell’asymmetric drift mostra
come nel caso in qui la velocità media di un tracciante coincide con la velocità circolare, la
dispersione di velocità è nulla. Un valore basso della dispersione di velocità genera una riga di
emissione stretta. Nelle regioni del bulge è possibile che le righe del gas ionizzato abbiano una
dispersione di velocità maggiore. Per misurare la lunghezza d’onda di una riga di emissione si
interpola il profilo della riga con una Gaussiana determinandone la lunghezza d’onda media, la
larghezza e l’intensità (Fig.3.1). Il redshift z è, per definizione,
z=
∆λ
λosservata
λosservata − λlab
=
−1
=
λlab
λ
λlab
(3.1)
Le principali righe di emissione nella regione visibile (compresa la riga ultravioletta Lyα che
17
Riga
λ
tipo Riga
Lyα
1215.67 EA Fe I
[O II]
3726.03
E
[O III] N1
[O II]
3728.82
E
[O III] N2
He II
3768.90
E
Mg I
He I
3833.57
E
Mg I
[Ne III]
3868.71
E
Mg I
He I
3888.65
E
[N I]
Hζ
3889.05 EA [N I]
Ca II K
3933.66 A Ca+Fe (E band)
[Ne III]
3967.41
E
He I
Ca II H
3968.47 A Na I
Hǫ
3970.07 EA Na I
Mn I
4033.00 A He II
Fe I
4045.81 A [O I]
Hδ
4101.73 EA [N II]
Ca I, g band 4226.73 A Hα
Fe I
4325.77 A [N II]
He II
4338.6
E
He I
Hγ
4340.46 EA [S II]
[O III]
4363.21
E
[S II]
Fe I
4383.55 A [Ar III]
He I
4471.50
E
[Ar IV]
Cr I
4666.00 A Ca II
He II
4685.68
E
Ca II
Hβ
4861.31 EA Ca II
λ
tipo
4920.51 A
4958.92
E
5006.84
E
5167.32 A
5172.70 A
5183.60 A
5197.90
E
5200.26
E
5269.00 A
5875.67
E
5889.95 A
5895.92 A
5977.00
E
6300.30
E
6548.03
E
6562.80 EA
6583.41
E
6678.15
E
6716.47
E
6730.85
E
7135.78
E
7237.30
E
8498.02 A
8542.09 A
8662.14 A
Table 3.1: Principali righe di emissione e assorbimento presenti negli spettri di galassie nella
regione ottica. E=emissione; A=assorbimento
18
Figure 3.1: Profilo delle righe di emissione interpolato con una gaussiana nelle regioni spettrali
dell’Hα e Hβ . le righe interpolate ed indicate con un numero sono [N II]λλ6548, 6583Å, Hα , [S
II]λλ6717, 6031Å, Hβ e [O III]λλ4959, 5007Å.
cade nel visibile in oggetti da alto z) con relative lunghezze d’onda a riposo sono elencate nella
tabella 3.1 . La misura di λ viene fatta lungo tutta la fenditura in modo da avere una misura
in diverse posizioni. Ricordiamo che diverse posizioni lungo la fenditura significano diverse
distanze dal centro della galassia (distanza galattocentrica). Questa distanza dal centro della
galassia sarà inizialmente misurata in arcsec (che è una unità legata all’osservazione) e verrà poi
trasformata in pc (che è una unità fisica, intrinseca della galassia) una volta nota la distanza
della galassia da noi. In Fig.3.2 è mostrato quello che si ottiene misurando la lunghezza d’onda
della riga Hα da uno spettro a fenditura lunga.
3.2
Trasformare z in velocità
La formula relativistica che lega il redshift z alla velocità radiale V di un oggetto è la seguente:
(z + 1)2 − 1
V =c
(z + 1)2 + 1
(3.2)
(c = velocità della luce nel vuoto = 299792.458 km/s) o anche
z=
v
u
u 1 + V /c
t
1 − V /c
(3.3)
Spesso si utilizza l’approssimazione valida per V << c (oppure z << 1). In questo caso
V = cz
(3.4)
È da notare però che si può commettere un errore sensibile anche a velocità dell’ordine del
migliaio di km/s come evidenziato nella figura 3.3
19
Figure 3.2: NGC 7339: misura della lunghezza d’onda della riga Hα in diverse posizioni lungo
la fenditura. in ordinata è riportata la distanza in arcsec dal centro della galassia.
Figure 3.3: (a) Differenza tra la velocità calcolata tramite la formula approssimate v = cz e
il valore corretto della velocità in funzione di quest’ultima; ((b) come (a) ma in funzione del
redshift z.
Il consiglio è quindi, quando possibile, di utilizzare sempre la formula corretta, specie se la
formula compare in un programma e non è necessario calcolare a mano la velocità. Questo è
anche il motivo per cui a volte nei cataloghi (ad esempio l’RC3) non si trova tabulato il valore
della velocità radiale di galassie ma il valore di cz.
20
Figure 3.4: Esempio di curva di rotazione e di dispersione di velocità lungo l’asse maggiore di
una galassia a spirale (NGC3717). I cerchi vuoti indicano le misure della componente di gas
ionizzato mentre i punti pieni rappresentano le misure della componente stellare. La velocità
di sistema è stata già sottratta. Nel riquadro superiore è riportata una immagine della galassie
nella stessa scala dei grafici e con la posizione della fenditura indicata. Nella scala superiore le
distanze sono indicate in kpc mentre la scala di velocità sul lato destro della figura indica la
velocità deproiettata.
3.3
Determinazione della velocità di sistema e del centro
della galassia
Assumendo che la curva di rotazione di una galassia sia simmetrica rispetto al suo baricentro,
è possibile determinare la posizione di questo trovando il centro di simmetria della curva di rotazione. Compiendo questa operazione si determina contemporaneamente la velocità di sistema
del baricentro della galassia che altro non è che la velocità radiale del centro stesso.
3.4
Correzioni della velocità di sistema
La velocita’ determinata nel paragrafo precedente è la velocità radiale osservata del nostro
oggetto astronomico (Vradiale ). Questa è il risultato della composizione di diversi moti. I principali sono (in ordine approssimativo di importanza):
21
i) Vcosmologica velocità della galassia dovuta all’espansione dell’universo
ii)Vp,gal velocità peculiare della galassia (cioè il moto della galassia rispetto a il sistema di riferimento in cui la radiazione di condo cosmico risulti ferma)
iii) Vp,Gal velocità peculiare della nostra galassia (ad esempio, sappiamo che la Galassia si sta
muovendo nella direzione del Grande Attrattore)
iv) Vsun moto di rotazione del sole attorno al centro della nostra galassia
v) Vrivoluzione moto di rotazione della terra attorno al sole
vi) Vdiurna moto di rotazione della terra attorno a se stessa
In altre parole
Vradiale = Vcosmologica + Vp,gal + Vp,Gal + Vsun + Vrivoluzione + Vdiurna
(3.5)
Avendo a che fare con velocità radiali siamo interessati solo alla proiezione delle velocità
lungo la linea di vista. Dato che per determinare la distanza di una galassia si utilizza in
genere la legge di Hubble che lega la distanza a Vcosmologica, quello che a noi interessa è derivare
quest’ultima.
Vdiurna è spesso trascurabile. Dipende dalla direzione ove si sta osservando (cioè coordinate
celesti R.A., dec. e dall’ora siderale) e dalla posizione dell’osservatore sulla terra. Può essere al
massimo di ∼ 0.5 km/s e quindi inferiore alla precisione degli strumenti normalmente impiegati
per la misura di cinematica di galassie.
Vrivoluzione Dipende dalla direzione ove si sta osservando (cioè coordinate celesti R.A., dec. e
dall’ora siderale) e dalla posizione dell’osservatore sulla terra. Può valere al massimo 33 km/s e
è quindi necessario tenere in considerazione tale correzione. La formula completa per calcolare
tale correzione è complessa. I normali pacchetti di riduzione dati comprendono algoritmi in
grado di eseguire tale conti (rvcorrect per IRAF, comp/bary per MIDAS)
Vsun e Vp,Gal . Non è necessario conoscere separatamente questi due termini. Le misure del moto
del sole rispetto alla radiazione di fondo cosmico forniscono infatti, e con buona precisione,
la attuale velocità e direzione di tale moto che è dovuto alla composizione di Vsun e di Vp,Gal .
la correzione da apportare alla velocità osservata dipende in questo caso solo dalla posizione
dell’oggetto sulla sfera celeste. Normalmente si fa uso delle coordinate galattiche l (longitudine)
e b (latitudine). I valori attuali della posizione dell’apice e del valore della velocità sono:
lapex = 264.14◦, bapex = +48.26◦ , Vapex = 371.0 km/s e la formula per calcolare la correzione è
∆V3KB = Vapex [sin(b) sin(bapex ) + cos(b) cos(bapex ) cos(l − lapex )]
(3.6)
Vp,gal Non vi è alcun modo per trovare questa quantità conoscendo solo la velocità radiale
osservata. In ammassi di galassie come quello del Virgo è possibile trovare galassie con Vp,gal ∼
1000 km/s.
Alla fine avremo quindi
Vcosmologica = Vradiale + ∆V3KB + Vrivoluzione
3.5
Distanza e scala della galassia
Nota Vcosmologica possiamo determinare la distanza del nostro oggetto tramite la legge di Hubble.
Nel caso di velocità piccole possiamo utilizzare la formula approssimata
D = Vcosmologica /H0 ; H0 = 73 km/s/Mpc
22
(3.7)
Ad esempio, una galassia con Vcosmologica = 2000 km/s si trova ad una distanza di 27. 4Mpc.
Misurando V in km/s otteniamo la distanza direttamente in Mpc. Nota la distanza possiamo
derivare la scala delle distanze sulla galassia:
scala = D/206264.8 = D(Mpc)/.2062648
(3.8)
Ad esempio, nel caso precedente abbiamo circa 133 pc/arcsec. Siamo quindi in grado di indicare
le distanze sulla galassia in unità fisiche. Diverso è il discorso nel caso di velocità relativamente
alte. In questo caso il formulario da utilizzare è più complesso. Innanzitutto si distingue fra
distanza angolare DA e distanza in luminosità DL . DA si usa per calcolare la scala angolare
secondo l’usuale formula
scala = DA /206264.8
(3.9)
mentre DL si usa per calcolare la luminosità
modulo di distanza = 5 − 5 log(DL(pc))
(3.10)
Per calcolare DL e DA è necessario calcolare la distanza comovente DM che dipende dal tipo
di universo che si considera ed è data da
c
DM (z) =
H0
Z
0
z
q
z′
ΩM (1 + z ′ )3 + ΩΛ
(3.11)
con DA = DM /(z + 1) e DL = DM (z + 1) (e quindi DA = DL /(z + 1)2 . Per comodità, in
appendice A.3 riportiamo una tabella con il valore di DM , DL e DA (e modulo di distanza e
“look back time”) per diversi valori di z.
3.6
Deproiezione e passaggio a grandezze fisiche
A questo punto non rimane che deproiettare le quantità osservate. Infatti noi vediamo le distanze proiettate sul piano del cielo e le velocità proiettate lungo la linea di vista. Consideriamo
il caso in cui il gas ionizzato sia disposto in un disco infinitamente sottile e che si muova di
moto circolare attorno al centro della galassia. Nel piano del cielo indichiamo al posizione con
Figure 3.5: Sistema di coordinate nel piano della galassia (destra) e del cielo (sinistra)
le coordinate x, y (3.5). Sempre nel piano del cielo indichiamo l’angolo rispetto all’asse maggiore apparente (che coincide con la linea dei nodi del disco) con φ e le distanze dal centro
della galassia con r. Nel pano del disco queste ultime due grandezze le indichiamo con θ ed R.
Indichiamo inoltre con i l’inclinazione del disco. i = 90◦ indica un disco visto di taglio mentre
23
i = 0◦ è l’inclinazione di un disco visto perfettamente di faccia. Con queste definizioni si può
dimostrare che valgono le seguenti formule di proiezione:
tan θ =
tan Φ
cos i
(3.12)
Se indico con V (r, Φ) la velocità osservata e con Vdep (R) la velocità intrinseca
V (r, Φ) = Vdep (R) cos θ sin i; R = r
cos Φ
cos θ
(3.13)
In questo modo per ogni punto osservato in cielo in posizione (r, Φ) posso calcolare la posizione
sul piano della galassia (R, θ) e calcolare la velocià deproiettata Vdep . Nel caso particolare e
frequente in cui le velocità sono state misurate lungo l’asse maggiore, posso scrivere Φ = 0◦ ,
θ = 0◦ e quindi R = r e V (r) = Vdep (R) sin i. Per deproiettare le velocità basta quindi dividere
le velocità osservate per il seno dell’inclinazione i mentre le distanze dal centro della galassia
non hanno bisogno di deproiezione. Esaminiamo ora 2 campi di velocità particolari: moto
rigido e velocità costante
3.6.1
Proiezione del campo di velocità di un moto rigido
Una legge di velocità in cui questa è proporzionale alla distanza dal centro si dice rigido:
V (R)dep = ΩR
Una velocità con queste caratteristiche si trova spesso nella zona centrale delle galassie. In
questo caso si vede che, dato che nel piano del cielo x = r cos φ, posso scrivere
V (x, y) = ΩR cos θ sin i = Ωr
cos Φ
cos θ sin i = Ωx sin i
cos θ
(3.14)
Il campo di velocità avrà un’aspetto come indicato in Fig.3.6 (sinistra)
Figure 3.6: Campo di velocità proiettato dato da un moto rigido (destra) e da una velocità
costante (sinistra)
3.6.2
Proiezione del campo di velocità V=costante
Le curve di rotazione nelle regioni esterne delle galassie a disco mostrano spesso un valore
costante di velocità. Vediamo quindi come appare in 2 dimensioni un campo di velocità di
questo tipo proiettato in cielo.
V (R)dep = V0
24
Si può vedere che le equazioni 3.12 e 3.13 possono essere scritte in questo caso
V (r, Φ) = V0 cos θ sin i = V0 √
sin i cos i
cos2 i + tan2 Φ
(3.15)
Questo è il campo di velocità proiettato e dipende solo da Φ, cioè l’angolo di posizione in cielo.
Il campo di velocità risultante è mostrato in Fig.3.6 (destra).
3.6.3
Campi di velocità reali
Un campo di velocità reale è simile ad un moto rigido nel le regioni centrali e tende ad avere
una V=costante nelle regioni esterne. Il risultato lo si può vedere dagli esempi mostrati in
Fig.3.7 Altrimenti siete in grado di riconoscere nel campo di velocità di Fig.3.8 quello generato
Figure 3.7: Campo di velocità proiettato dato un moto rigido al centro e V=costante nelle
regioni esterne (destra) e campo di velocità derivato dalla riga HI in un caso reale (sinistra)
Figure 3.8: Campo di velocità (sinistra) proiettato in cielo generato dalla curva di rotazione
mostrata (sinistra).
dalla curva di rotazione mostrata in quella stessa figura ?
25
Chapter 4
Effetti strumentali e osservativi che
influenzano le misure cinematiche
Vi sono due fattori che maggiormente influenzano le misure di cinematica a fenditura lunga.
Queste sono il seeing atmosferico e la larghezza della fenditura. Tipici valori di seeing e larghezza
della fenditura sono dell’ordine di qualche secondo d’arco o frazione di secondo d’arco (tipicamente da 0.5′′ a 3′′ per osservazioni da terra). Nel caso di galassie vicine la misura della
cinematica viene deteriorata in maniera minima e non è sempre necessario tenere conto di
questi effetti. E’ invece importante nel caso in cui le caratteristiche che vogliamo osservare
variano significativamente su scale angolari come quelle indicate. Nel caso di galassie lontane
siamo nella situazione in cui la fenditura comprende la luce di una significativa porzione di
galassia. In Fig.4.1 riportiamo come esempio come appaiono galassie a spirale a redshift vicino
ad 1. Una fenditura larga 1.5” copre una porzione notevole di galassia.
Figure 4.1: In questa figura mostriamo, come esempio, l’immagine di tre galassie a spirale a
redshift z=0.65, 0.68 e 0.97. Il campo di vista e’ di 6′′ × 6′′ .
4.1
Convoluzione per Point Spread Function
La Point Spread Function (PSF e cioè “funzione di allargamento”) non è altro che l’immagine
con cui viene vista una sorgente che per natura è puntiforme. Per immagini prese da terra la
PSF è per lo più dovuta al “seeing” atmosferico. Non è escluso che altri fattori possano però
contribuire (messa a fuoco del telescopio e dello strumento, cattivo inseguimento del telescopio
o anche PSF dovuta al CCD o all’apertura del telescopio, etc.). Per molte applicazioni la PSF
viene assunta avere forma gaussiana bidimensionale ed è caratterizzata dal valore di σ (NOTA.
quando si indica il valore del seeing spesso si dà il valore della FWHM che vale 2.3548σ).
26
L’espressione per una PSF gaussiana è
P SF (x, y) = exp(
−x2 − y 2
)
2
2σseeing
(4.1)
dove (x, y) sono le coordinate nel piano del cielo secondo un sistema di assi ortogonali.
Sia I(x, y) la luce proveniente da una galassia. A causa della PSF verrà osservata una
immagine Ioss (x0 , y0) che è la convoluzione di I(x, y) con la PSF e cioè:
I(x0 , y0 )oss =
4.1.1
Z
I(x, y)P SF (x − x0 , y − y0 )dxdy
(4.2)
Metodo approssimato: convoluzione del campo di velocità
Nel caso di misure cinematiche l’effetto è in prima approssimazione simile a quanto avviene per
le immagini. La PSF di fatto fa “muovere” l’immagine rispetto alla fenditura dello spettroscopio. Dato che diverse zone della galassia hanno diverse velocità radiali, la velocità Voss (x, y)
effettivamente misurata nella posizione (x, y) sarà la convoluzione del campo di velocità V (x, y)
intrinseco per la PSF pesata però per l’intensità I(x, y). In questo modo si tiene conto del fatto
che la posizione (x′ , y ′) ,vicina a (x, y), influisce sulla velocità Voss (x, y) non solo a seconda di
quanto tempo il punto (x′ , y ′) passa per la posizione (x, y) a causa della PSF ma anche della
sua intensità. In altre parole la convoluzione sarà data dall’integrale
Voss (x0 , y0) =
Z
V (x, y)I(x, y)P SF (x − x0 , y − y0 )dxdy
(4.3)
Lo stesso si può dire per altri parametri cinematici come la dispersione di velocità σ
σoss (x0 , y0) =
Z
σ(x, y)I(x, y)P SF (x − x0 , y − y0 )dxdy
(4.4)
È importante ricordare che anche se la convoluzione è una operazione univoca, la deconvoluzione non lo è. Sappiamo cioè convolvere una immagine perfettamente ma non deconvolverla. Questo è il motivo per cui generalmente, quando si confrontano i dati osservativi
con un modello si preferisce convolvere quest’ultimo piuttosto che deconvolvere le osservazioni.
Dato che i modelli dipendono da parametri, quello che si fa è il trovare i parametri relativi al
modello che meglio riproduce le osservazioni
Nelle equazioni 4.3 e 4.4 le quantità note sono Voss e σoss e la PSF. V e σ del modello sono
noti per ogni scelta dei parametri che li caratterizzano. la funzione I(x, y) non è nota a priori.
È l’intensità intrinseca della galassia che stiamo osservando. si potrebbe utilizzare Ioss (x, y) o
tentare di deconvolvere questa, introducendo però ulteriori incertezze nella convoluzione.
Una possibile soluzione sta nell’utilizzare immagini prese da telescopi orbitanti (come HST
l’archivio del quale, accessibile a tutti, contiene ormai molte immagini di galassie). Queste
immagini non sono affette da seeing atmosferico e sono caratterizzare da una PSF dovuta
esclusivamente allo strumento. HST ha una PSF che nelle bande ottiche e’ dell’ordine di 0.05”.
Combinando immagini da satellite con cinematica da terra è possibile quindi condurre una
analisi cinematica che tenga parzialmente conto della PSF.
Dal punto di vista concettuale possiamo notare che abbiamo prima misurato i parametri
cinematici (V , σ, etc.) e poi operato la convoluzione.
27
4.1.2
Convoluzione del cubo di dati
Il tipo di convoluzione descritto nella sezione precedente è valido nel caso in cui non vi sia una
variazione troppo brusca delle velocità su dimensioni paragonabili o inferiori a quelle della PSF.
Questo è il caso di galassie vicine dove il gradiente di velocità osservato è in genere inferiore a 100
km/s/arcsec. Questo può non essere vero per galassie più lontane dove la velocità massima può
essere raggiunta già a 1” dal centro o per galassie anche vicine ma con un gradiente di velocità
centrale particolarmente elevato. In questo caso il profilo della riga di emissione misurato sullo
spettro può assumere una forma a doppio picco o asimmetrica, comunque molto distante dalla
forma gaussiana. Il modo corretto di confrontare la previsione del modello cinematico (I(x, y),
V (x, y), σ(x, y) ed eventualmente ordini superiori quali, ad esempio, h3 (x, y) e h4 (x, y); vedi
sez.5.6) con le osservazioni è quello di convolvere il modello prima di operare la misura degli
osservabili. Questo è di fatto quello che avviene al telescopio.
Il modo più pratico di eseguire la convoluzione è quello di generare le immagini monocromatiche della nostra galassie, convolverle per la PSF e successivamente misurare i parametri cosı̀
come li abbiamo misurati sullo spettro ottenuto al telescopio. La PSF agisce sui fotoni modificando la forma dell’immagine che andranno a formare, ma non ne cambia la lunghezza d’onda.
Per ”immagine monocromatica” si intende la mappa di intensità nel piano del cielo ad una
lunghezza d’onda ben precisa. In pratica, dato che lo scopo è quello di simulare l’osservazione
della galassia modello, si utilizzeranno le stesse lunghezze d’onda a cui vengono presi i dati
spettroscopici. L’immagine monocromatica si costruisce dal modello. Nel caso in cui il modello
cinematico di galassia considera I(x, y), V (x, y) e σ(x, y) ed il profilo della riga è gaussiano
(plausibilmente il modello di galassia è tridimensionale ma nel nostro esempio partiamo dal
modello spazialmente già proiettato nel piano del cielo e le velocità proiettate lungo la linea di
vista) l’intensità alle varie lunghezze d’onda si può calcolare come
I(x, y, λ) = I(x, y)exp(
−(λ − λV (x, y))2
2σ 2 (x, y)
λV (x, y) = (V (x, y)/c + 1)λ(riga)
(4.5)
(4.6)
dove per λ(riga) intendiamo la lunghezza d’onda a riposo della riga di emissione che si sta
considerando (vedi Tab.3.1). In fig.4.2 mostriamo uno schema illustrativo di quanto descritto
dalla eq.4.5
La mia immagine monocromatica per λ = λ0 è allora I(x, y; λ0) e può essere convoluta per
la PSF
Z
Ioss (x0 , y0 ; λ0 ) = I(x, y; λ0)P SF (x − x0 , y − y0 )dxdy
(4.7)
Per completare la convoluzione del modello devo eseguire tante convoluzioni quante sono le
immagini monocromatiche che interessano la mia riga di emissione. (Dato che la convoluzione
è una delle operazioni più lente, questa tecnica risulta notevolmente più lenta come tempo di
calcolo rispetto alla semplice convoluzione del campo di velocità descritta nella sezione precedente.) Come si può notare, i dati sono rappresentabili con un grafico a 3 dimensioni in cui
2 dimensioni sono quelle spaziali e la terza è la lunghezza d’onda. Tale insieme di dati viene
definito ”datacube” o cubo di dati (Fig.4.3). Una volta convoluto il ”datacube”, e cioè sono
state convolute tutte le immagini, si può estrarre i singoli spettri
I(λ; x0 , y0) = Ioss (λ; x0 , y0)
ed interpolarli per ottenere Voss (x0 , y0 ), σoss (x0 , y0 ), h3,oss (x0 , y0 ), h4,oss (x0 , y0 ) per confrontarli
con quanto osservato. Volendo è anche possibile confrontare I(λ; x0 , y0 ) direttamente con le
osservazioni.
28
Figure 4.2: Esempio schematico di “datacube”. Per ogni posizione (x, y) il modello ci fornisce
l’intensità alle varie lunghezze d’onda. Possiamo quindi estrarre una immagine monocromatica,
ad esempio per λ0 . In questa figura le due posizioni poste più in alto per λ = λ0 danno una
intensità pari a 0 mentre nel terzo punto, a causa del particolare redshift, abbiamo una intensità
I 6= 0.
Figure 4.3: Un “datacube” può essere visualizzato come uno spettro a fenditura lunga se se ne
prende una sezione parallelamente all’asse della lunghezza d’onda o come immagine monocromatica se se ne prende una sezione perpendicolarmente all’asse della lunghezza d’onda.
29
4.2
Fenditura grande rispetto alla galassia.
Vi sono situazioni in cui la fenditura ha dimensioni maggiori della PSF. Questo è sempre vero
quando si utilizza lo spettroscopio STIS montato su HST (la quasi totalità dei dati relativi
a buchi neri supermassici in galassie viene da questo strumento). Quando ci troviamo nella
situazione appena descritta non si può trascurare la posizione entro la fenditura da cui viene
l’emissione. L’informazione spaziale si sovrappone alla informazione in lunghezza d’onda. Due
sorgenti posizionate nella stessa posizione x (vedi Fig.4.4) lungo al fenditura, ma in una diversa
includegraphics[width=6cm]slit.eps
Figure 4.4: In questo disegno due sorgenti di emissione si trovano nella stessa posizione x lungo
la fenditura, ma in una diversa posizione s ortogonalmente a questa. Pur emettendo una riga
identica come λ e σ, sembrano avere due lunghezze d’onda diverse.
posizione s. Pur emettendo una riga identica come λ e σ, sembrano avere due lunghezze d’onda
diverse solo perché sono in posizioni diverse l’una rispetto all’altra.
Un esempio pratico di quanto discusso nelle ultime due sessioni si puó trovare nell’articolo
di Metevier et al (2006 ApJ, 643, 764) che misurano la curva di rotazione di un campione di 15
galassie a z = 0.4 utilizzando spettrosocpia a fenditura lunga. Gli autori ricordano che
... Misurare le velocitá di rotazione di galassie distante da spettir ottici é un lavoro impegnativo che comporta il confronto tra le emissioni osservate e un modello di emissione. In
parte questo é dovuto al fatto che a z ∼ 0.4 le dimensioni tipiche di una galassia sono di 1′′ e
cioé equivalenti alle dimensioni del disco del seeing e alla larghezza della fenditura. Per questo
motivo lo spettro conterrá le informazioni di distribuzione della luce e delle velocitá di gran
parte della galassia. La curva di rotazione che si ricava é ben lungi da quella che si ottiene da
una usuale fenditura lunga e sottile posta lungo l’asse magigore di una galassia. Ecco un elenco
di quelli che possono essere i fattori di cui é necessario tenere conto quando si vul convertire lo
spettro di emissione grezzo in una velocitá di rotazione per galassie lontane:
1. La distribuzione spaziale della emissione della galassia
2. LOSVD dell’emissione
3. inclinazione del disco
4. effetto del seeing
5. effetto dello strumento
6. dimensione della fenditura rispetto alle dimensioni della galassie
7. angolo di posizione della fentitura
8. posizione della fenditura rispetto al centro della galassia
...
Gli autori utilizzano due approcci alternativi per determinare la curva di rotazione delle
galassie. Un primo approccio, che chiamano GAUS2D, consiste nel confrontare le velocitá
misurate con una interpolazione gaussiana degli spettro osservati e del modello. Il secondo
approccio, che chiamano GELFIT2D, consiste invece nel confrontare direttamente l’emissione
oservata con il modello senza interpolare le righe di emissione con gaussiane. Il punto 1) della
30
lista viene determinato da immagini ottenute con HST che, rispetto alle osservazioni di cinematica che sono effettuate da terra, sono considerate virtualmente non affette da seeing; il punto
2) viene risolto costruendo un modello per le velocitá che vengono considerate perfettamente
circolari e descritte dalla curva di rotazione che segue la legge empirica
V (r) =
r
2Varc
arctan( )
π
rto
(4.8)
dove Varc é la velocitá asintotica e rto é un raggio di scala (troveremo questa formula parlando
della curva di rotazione delle galassie a spirale e della materia oscura); il punto 3) viene risolto
derivando l’inclinazione dall’immagine HST; il punto 4) viene risolto convolvendo il modello
per il seeing; i punti 5) e 6) vengono tenendone conto nel modello; i punti 7) ed 8) vengono
risolti individuanto, in base all’immagine HST, l’esatta posizione ed orientazione della fentidura
sull’immagine della galassia ed estraendo quindi lo spettro in maniera appropriata. Per tre delle
galassie il risulltato é mostrato in fig.4.5.
31
Figure 4.5: Esempio di misura di cinematica da una riga di emissione per galassie a z = 0.4.
L’immagine indicata con F814W e’ ottenuta con HST in banda I ed é indicata la posizione della
fentidura. La label GIM2D indica come il modello ha riprodotto la distribuzione della luce della
galassia. residual indica l’immagine differenza tra le osservazioni HST e il modello fotometrico.
Le finestre successive mostrano lo spettro di una riga di emissione (Hα o [OIII]) osservata (a
sinistra), l’emissione del modello (nel centro) e il residuo osservato-modello (destra) secondo
il modello GELFIT2D. L’ultima finestra a destra mostrail confronto tra la curva di rotazione
misurata con le gaussiane ed il modello GAUS2D.
32
Chapter 5
Misura della cinematica della
componente stellare
Vi sono galassie prive di gas ionizzato per le quali è possibile ricavare informazioni dinamiche
solo dalla componente stellare. È il caso delle galassie ellittiche ed S0. A differenza del gas
ionizzato, il cui spettro è caratterizzato da forti righe di emissione, lo spettro della componente
stellare è caratterizzato da righe di assorbimento. La misura della cinematica risulta più difficoltosa essenzialmente per i seguenti motivi:
1) Gli assorbimenti sono più deboli delle emissioni. Più precisamente, la riga di assorbimento è
sempre più debole del continuo stellare. In altre parole, dove non ho luce, non ho assorbimento.
(Questo non è vero per la componente gassosa. È possibile individuare righe di emissione anche
in regioni del disco dove la brillanza superficiale è estremamente bassa.)
2) Non esistono righe di assorbimento isolate. Le righe di assorbimento sono spesso in “blend”
(sono cioè fuse) con righe vicine. Non vi sono righe di assorbimento isolate per le quali si possa
misurare la lunghezza d’onda e larghezza con una semplice interpolazione gaussiana come generalmente si fa per il gas ionizzato.
3) Il gas ionizzato ha una dispersione di velocità generalmente molto bassa e dinamicamente
spesso ininfluente. La componente stellare invece ha una dispersione di velocità che può essere
dinamicamente più rilevante della velocità stessa come nel caso delle galassie ellittiche. È quindi
necessario misurare sia V che σ.
Per questi motivi storicamente si è riusciti a misurare prima la rotazione delle galassie a
Spirale e solo successivamente la cinematica delle galassie ellittiche.
5.1
Effetto del redshift sullo spettro
La cinematica stellare viene misurata non dall’analisi di singole righe di assorbimento, ma
dall’analisi di una regione spettrale relativamente estesa. In passato veniva molto usata la
regione 3700 − 4100Å dove vi sono le forti righe CaII H e K, Ora è più frequente l’utilizzo
della regione 4700 − 5400Å dove incontriamo sia l’Hβ che le righe del MgI (tripletto) Fe e Ca
oppure nella regione più rossa 8400 − 8900Å attorno al tripletto del CaII (vedi Tab.3.1). Il
redshift agisce sullo spettro emesso dalle stelle della galassia spostandolo verso il rosso. È però
importante notare che tale spostamento non è lo stesso alle varie lunghezze d’onda. Essendo
∆λ
λ − λ0
z=
=
≈ V /c
(5.1)
λ0
λ0
(per piccoli valori di z). Si può facilmente ricavare che
λ = λ0 (1 + V /c)
33
(5.2)
o anche
∆λ = λ0 V /c ∝ λ0
(5.3)
Ad esempio, se la lunghezza d’onda di 3000Å viene spostata a 4000Å, la lunghezza d’onda
6000Å viene spostata a 8000Å. Se consideriamo ln(λ) anziché λ allora
ln(λ) = ln(λ0 ) + ln(1 + V /c)
(5.4)
ln(λ) − ln(λ0 ) = ∆(ln(λ)) = ln(1 + V /c) ≈ V /c
(5.5)
e quindi
La dipendenza da λ0 è sparita e lo spettro è spostato di una quantità costante ≈ V /c.
5.2
Definizione di LOSVD
Introduciamo il concetto di distribuzione delle velocità lungo la linea di vista o più brevemente LOSV D(v) (Line Of Sight Velocity Distribution). Questa non è altro che l’intensità
dell’emissione proveniente da gas con velocità radiale v oppure, se stiamo considerando la cinematica della componente stellare, la LOSV D(v) sarà la funzione che mi indica che percentuale
di stelle hanno velocità radiale v. Ad esempio una LOSVD gaussiana avrà la forma
√
(5.6)
LOSV D(v; V, σ) = NORM × exp(−((v − V )/ 2σ)2 )
In questo caso conoscere la LOSVD significa conoscere V e σ. Il gas ionizzato ha tipicamente
una LOSVD gaussiana con σ di poche decine di km/s. Essenzialmente la LOSVD è l’incognita
del nostro problema. Misurare la cinematica stellare (e anche gassosa) significa determinarne
la LOSVD.
5.3
Spettro delle galassia come convoluzione
In virtù della eq.5.5 possiamo vedere come lo spettro si (lnλ) (dove per comodità indichiamo
con lnλ il termine ln(λ)) di una generica stella i con velocità radiale v verrà visto da terra come
siv (lnλ)
=
Z
si (lnλ′ )δ(lnλ′ − lnλ − v/c)dlnλ′
(5.7)
(dove la funzione δ indica la “delta di Dirac”). si (lnλ) sarà sempre uguale a 0 e sarà diversa da
zero solo quando lnλ′ − lnλ − v/c = 0. Si tratta di una traslazione si si (lnλ) di una quantità
pari a v/c. Quando osserviamo una galassia, salvo galassie del gruppo locale, non riusciamo a
risolvere le singole stelle. Lo spettro che vediamo è la somma di migliaia di stelle. A rigore lo
spettro di una galassia potremmo quindi descriverlo matematicamente come
G(lnλ) = Σi
Z
si (lnλ′ )δ(lnλ′ − lnλ − v i /c)dlnλ′
(5.8)
dove la somma viene intesa su tutte le stelle i, ciascuna con il suo spettro si e la sua velocità
v i . Di fatto si può vedere che lo spettro di una galassia ellittica è ben riprodotto dallo spettro
di una stella gigante di tipo G8-K3 che indico d’ora in avanti semplicemente come s(lnλ). Tale
spettro viene indicato con il nome di spettro “template” o spettro campione. Si assume essere
uguale allo spettro di una galassia formata da stelle ferme. Galassie di questo tipo non esistono
per cui si supplisce utilizzando lo spettro di una stella gigante di tipo G8-K3. Dato che lo
spettro s(lnλ) non dipende più dalla stella i posso invertire la sommatoria con l’integrale, ma
34
la sommatoria delle delta ognuna con la velocità della stella non è altro che la LOSVD (se
vogliamo, per definizione di LOSVD). Posso allora riscrivere l’ultima equazione come
G(lnλ) =
Z
s(lnλ′ )LOSV D(lnλ − lnλ′ )dlnλ′
(5.9)
Le singole stelle di una galassia, a parte la velocità di allontanamento da noi dell’intero sistema
dovuto all’espansione dell’universo, avranno velocità leggermente diverse l’una dall’altra. Sappiamo ad esempio che nei dintorni solari nella nostra Galassia le stelle hanno una dispersione di
velocità (ellissoide delle velocità) dell’ordine di 20 − 40 km/s. Mi aspetto che lo stesso avvenga
per galassie a spirale diverse dalla nostra. Ci si può insomma aspettare che la LOSVD possa
avere una forma vicina a quella gaussiana. In questo caso, cioè se la LOSVD è rappresentata
da una distribuzione gaussiana, posso scrivere
G(lnλ) =
Z
−(lnλ′ − lnλ − V /c)2
√
s(lnλ )exp(
)dlnλ′
2
2(σ/c)
′
dove V e σ sono la velocità media e la dispersione di velocità lungo la linea di vista.
(5.10)
Nella
Figure 5.1: Convoluzione dello spettro della stella template (rosso) con una LOSVD gaussiana.
V e σ della LOSVD sono indicati per ogni grafico. In ascissa viene riportata la lunghezza
d’onda in Å.
figura 5.1 viene mostrato lo spettro di una galassia confrontato con quello si una stella convoluta
con LOSVD gaussiana e diversi valori di V e σ. Nelle varie figure 5.1(a)-(e) si può notare che:
(a) lo spettro di stella e galassia sono simili ma la stella deve essere spostata verso il rosso;
(b) non basta spostare verso il rosso, le righe della galassia sono più larghe. È quello che ci si
aspetta; (c) il valore di σ utilizzato ancora troppo basso; (e) σ utilizzata troppo alta; (d) qui lo
spettro della galassia sembra essere ben riprodotto, specie nella regione 5250 − 5900Å. Siamo
quindi riusciti a stimare sia il valore di V che di σ della galassia osservata.
35
Figure 5.1: continua.
5.4
Determinazione della LOSVD
Come abbiamo già detto, determinare la cinematica di una galassia significa in pratica determinare la LOSVD. L’esempio riportato in Fig5.1 è un utile esercizio, ma non permette una
misura accurata di V e σ. Diverse sono le tecniche che permettono di ottenere questa informazione. Tutte utilizzano lo spettro di una stella template (o eventualmente più d’uno nel caso
si voglia tenere conto della presenza di diversi tipi spettrali) e sono quindi tutti, chi in maniera
minore, chi maggiore, effetti dal problema del cosı̀ detto “template mismatching”, e cioè dal
fatto che lo spettro della stella template è simile ma non perfettamente uguale a quello della
galassia, che è composta da stelle di vario tipo spettrale. Tale differenza si propaga aumentando l’incertezza con cui viene misurata la LOSVD. Le tecniche principali di determinazione
della LOSVD sono: 1) interpolazione diretta. 2) Fourier quotient (vedi sec.5.5) 3) Funzione di
correlazione 4) Espansione in somma di gaussiane.
1) interpolazione diretta. In pratica si minimizza la differenza tra lo spettro della galassia e
36
della stella dopo averla convoluta con un opportuno valore di V e σ. O meglio, si trovano i valori
di V e σ (o altri parametri che definiscono la LOSVD che sto considerando) che minimizzano
lo scarto quadratico medio tra lo spettro della galassia e della stella convoluta. Vantaggi di
questo metodo vi sono la possibilità di mascherare (ovvero non considerare quando si esegue il
confronto tra spettro della template e galassia) le regioni dello spettro “disturbate” ad esempio
da forti righe spettrali del cielo. È un metodo molto sensibile al template mismatching in
quanto quando lo scarto è alto non è a priori noto se il problema consiste in un non adeguato
valore di V e σ oppure in una differenza intrinseca tra lo spettro della template e della galassia.
Questa caratteristica può essere utilizzata a proprio vantaggio se si vuole determinare, oltre alla
cinematica, la composizione della popolazione stellare. Per fare questo, una volta determinato il
valore migliore per V e σ anche se affetti da template mismatching, si genera uno spettro stellare
artificiale, da utilizzare come nuovo spettro template, come combinazione lineare di spettri di
stelle di diverso tipo spettrale. Una nuova interpolazione tra lo spettro della galassia e quello
della nuova template convoluta permetter di determinare quali sono i migliori coefficienti della
combinazione lineare di spettri, e cioè la percentuale dei vari tipi spettrali che compongono lo
spettro della galassia.
3) Funzione di correlazione.
4) Espansione in somma di gaussiane. La trasformata di Fourier di una gaussiana è sempre una
gaussiana. Parametrizzare la LOSVD come somma di gaussiane semplifica matematicamente
il problema nel caso si voglia considerare una LOSVD con forma diversa da una gaussiana.
5.5
Fourier Quotient
Un metodo molto usato in passato e didatticamente utile, è il Fourier Quotient. Tale metodo
si basa sulla considerazione che la convoluzione diventa, nello spazio di Fourier, una semplice moltiplicazione. Posso allora scrive l’equazione 5.9 , che è la convoluzione di s(lnλ) con
LOSV D(lnλ) come
g D
G̃ = s̃ × LOSV
(5.11)
dove il segno ∼ indica la trasformata di Fourier. I termini G̃ e s̃ sono noti dalle osservazioni.
Posso allora ricavare
g D = G̃/s̃
LOSV
(5.12)
g D posso ricavare LOSVD applicando una anti-trasformata di Fourier.
Una volta nota LOSV
L’operazione viene ripetuta per gli spettri G nelle varie posizioni della galassia in modo da
ottenere la misura della cinematica nella zona osservata (ad esempio lungo la fenditura se si
tratta di spettroscopia a fenditura lunga) e ricavare la curva di rotazione V(r), di dispersione
di velocità σ(r) etc.
5.6
Momenti di ordine superiore: h3 ed h4
Quando il rapporto segnale/rumore di uno spettro è sufficientemente alto, è possibile misurare
non solo l’intensità, la velocità e la dispersione di velocità di una riga, ma anche caratteristiche
di ordine superiore come la asimmetria (skewness) e la piattezza (kurtosis).
Dal punto di vista matematico posso caratterizzare la LOSV D in base al valore dei momenti
di diverso ordine. La velocità è il momento centrale di ordine 1:
V =
R
v × LOSV D(v)dv
R
LOSV D(v)dv
37
(5.13)
la dispersione è il momento di ordine 2 rispetto a V:
σ=
R
(v − V )2 × LOSV D(v)dv
R
LOSV D(v)dv
(5.14)
allo stesso modo si possono definire momenti di ordine superiore come
R
(v − V )3 × LOSV D(v)dv
R
LOSV D(v)dv
(5.15)
(v − V )4 × LOSV D(v)dv
R
kurtosis =
LOSV D(v)dv
(5.16)
LOSV D(v) = I0 exp(−y 2 /2)(1 + h3 H3 (y) + h4 H4 (y))
(5.17)
skewness =
R
In pratica però per parametrizzare la forma della LOSVD non si utilizzano l skewness e la
kurtosis ma si utilizza l’espansione di Gauss-Hermite. Si descrive la LOSVD secondo la forma
con y = (v − V0 )/σ0 , I0 , V0 e σ0 l’intensità, la velocità e la dispersione di velocità delle righe,
H3 ed H4 sono i polinomi di Hermite di 3zo e 4to grado.
√
1 √
1
H3 (x) = √ (2 2x3 − 3 2x); H4 (x) = √ (4x4 − 12x2 + 3)
6
24
(5.18)
H3 descrive le deviazioni asimmetriche dalla forma gaussiana e quindi il coefficiente h3 sarà
tanto più alto tanto più la LOSVD è asimmetrica. H4 descrive le deviazioni simmetriche dalla
forma gaussiana come la piattezza o l’acutezza e quindi il coefficiente h4 sarà tanto più alto
tanto più tali caratteristiche sono presenti. Una descrizione efficace è data dalla fig.5.2.
Il vantaggio di utilizzare tale parametrizzazione sta nel fatto che le grandezze h3 ed h4 non
sono correlate in quanto i polinomi di Hermite sono una base ortonormale nello spazio dei
polinomi. Un errore indotto dal rumore nella misura di h3 o h4 non si ripercuote in un errore
sull’altro parametro.
L’utilizzo dei parametri h3 e h4 ha trovato maggior impiego nello studio della cinematica
stellare. A differenza delle righe di emissione del gas, che hanno generalmente forma gaussiana,
la LOSV D stellare ha spesso valori di h3 ed h4 diversi da zero.
5.7
Esempi di campi di velocità mono e bidimensionali
Per concludere, mostriamo alcuni esempi di cinematica. In Fig.5.3 si può notare come il gas
abbia una dispersione di velocità vicina a zero. Le stelle hanno una dispersione di velocità
maggiore e velocità media inferiore rispetto al gas, per effetto dell’asymmetric drift. Nel caso
delle galassie ellittiche (Fig.5.4) si può invece notare che la velocità di rotazione è più piccola
della dispersione di velocità. Le galassie ellittiche hanno infatti una forma triassiale (e non
assisimmetrica) in quanto non sono supportate dalla rotazione ma dalla dispersione di velocità.
38
Figure 5.2: Descrizione della forma della riga o LOSVD al variare dei parametri h3 ed h4 .
39
Figure 5.3: Curva di rotazione lungo l’asse maggior di galassie a spirale. Punti pieni indicano
la cinematica delle stelle, punti vuoti del gas. Sull’immagine della galassia è stata riportata la
posizione e dimensione della fenditura. Sono inoltre indicate le distanze in kpc e le velocità
deproiettate.
40
Figure 5.4: Velocità e dispersione di velocità per 4 galassie ellittiche. I punti ai due lati della
galassia sono stato riportati dallo stesso lato ed indicati con simboli vuoti e pieni.
41
Appendix A
A.1
Costanti utili
c = 299792.458 km/s velocità della luce nel vuoto
G = 4.3106 10−3(km/s)2 pc/M⊙
A.2
Formule utili
• D(Mpc) = V /H0 = V(km/s)/73 (H0 attualmente è stimato valore 73km/s/Mpc)
• scala(pc/”) = D(Mpc)/.2062648
• M(r) = V 2 r/G (approssimazione distribuzione di massa sferica e moti circolari)
A.3
Distanze per z 6≪ 0
In questa appendice tabuliamo il valori di DL , DA , DL (vedi sec. 3.5) al variare di z. La
tabella è stata calcolata considerando i valori di ( H0 = 65km/s/Mpc, ΩM = 0.3, ΩΛ = 0.7).
Ricordiamo che
DL = distanza di luminosità = DM (z + 1)
DA = distanza angolare = DM /(z + 1)
DM = distanza comovente
Vengono inoltre indicati il “look back time”, cioè l’epoca, indietro nel tempo, a cui la luce è
stata emessa, e il valore di cz/H0 , spesso utilizzato per misurare la distanza a basse z (dove
DM =DL =DA ).
42
z
.005
0.01
0.02
0.03
0.04
0.05
0.07
0.10
0.15
0.20
0.25
0.30
0.40
0.50
0.70
1.00
1.50
2.00
2.50
3.00
4.00
5.00
6.00
7.00
8.00
9.00
10.0
15.0
DL
Mpc
23.2
46.5
89.0
141.5
185.4
239.4
335.1
490.9
768.0
1050.4
1357.1
1667.0
2339.3
3045.5
4582.0
7110.6
11748.7
16734.8
21965.2
27378.1
38609.3
50237.0
62165.4
74326.5
86677.5
99188.3
111829
176535
DA
Mpc
22.9
45.5
85.5
133.4
171.4
217.1
292.7
405.6
580.7
729.4
868.6
986.3
1193.5
1353.5
1585.4
1777.6
1879.7
1859.4
1793.0
1711.1
1544.3
1395.4
1268.6
1161.3
1070.1
991.9
924.2
689.6
43
DM
Mpc
23.0
46.0
87.2
137.4
178.2
228.0
313.2
446.2
667.9
875.3
1085.7
1282.3
1670.9
2030.3
2695.3
3555.3
4699.4
5578.2
6275.7
6844.5
7721.8
8372.8
8880.7
9290.8
9630.8
9918.8
10166
11033
LBT cz/H0
Gyr
Mpc
0.10 23.06
0.15 46.12
0.28 92.24
0.40 138.4
0.57 184.5
0.70 230.6
0.99 322.9
1.39 461.2
2.00 691.8
2.61 922.4
3.20
1153
3.67
1384
4.60
1845
5.42
2306
6.78
3229
8.31
4612
9.98
6918
11.03
9224
11.73 11530
12.23 13840
12.87 18450
13.26 23060
13.52 27670
13.70 32290
13.80 36898
13.90 41510
14.00 46120
14.20 69183