DIAGNOSTICA DEI RESIDUI
Per valutare la bontà dei residui in un modello di regressione lineare esistono diverse possibilità,
alcune di tipo esplorativo basate sulla costruzione di opportuni grafici ed altri affidati all’uso di
particolari misure o test statistici.
Si consideri un modello di regressione multivariata in cui il tasso di risparmio di 50 paesi è messo
in relazione con alcune variabili demografiche e con il pil. Il dataset a cui si fa riferimento
appartiene al pacchetto faraway. Lo si carichi e se ne esplori la struttura attraverso l’help:
data(savings)
help(savings)
Si costruisce quindi un modello di regressione in cui il tasso di risparmio, (la variabile sr) è messo
in relazione con tutte le altre 4 variabili:
g<-lm(sr~pop15+pop75+dpi+ddpi,savings)
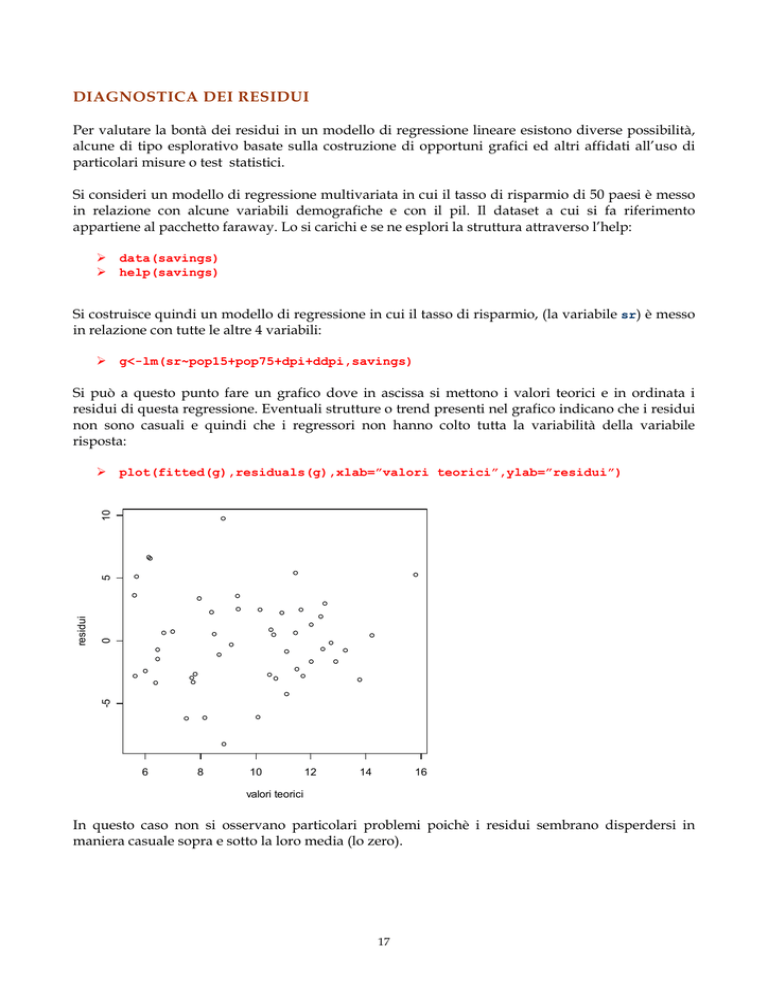
Si può a questo punto fare un grafico dove in ascissa si mettono i valori teorici e in ordinata i
residui di questa regressione. Eventuali strutture o trend presenti nel grafico indicano che i residui
non sono casuali e quindi che i regressori non hanno colto tutta la variabilità della variabile
risposta:
0
-5
residui
5
10
plot(fitted(g),residuals(g),xlab=”valori teorici”,ylab=”residui”)
6
8
10
12
14
16
valori teorici
In questo caso non si osservano particolari problemi poichè i residui sembrano disperdersi in
maniera casuale sopra e sotto la loro media (lo zero).
17
Verifica della normalità distributiva
La normalità distributiva dei residui si può esplorare innanzitutto in maniera grafica attraverso le
funzioni Q-Q plot.
Il comando qqnorm applicato ai residui del modello costruisce un grafico in cui riporta in ordinata
il valore osservato di ciascun residuo (i quantili campionari) mentre in ascissa rappresenta i valori
teorici (i quantili di popolazione) che delimitano la stessa frazione percentuale nella distribuzione
normale avente ugual media (nulla) e varianza di quella campionaria.
qqnorm(g$res)
Se la normalità distributiva è valida i punti tendono ad allinearsi lungo la bisettrice di questo
grafico. Per visualizzarne la bisettrice si digita il comando:
qqline(g$res)
0
-5
Sample Quantiles
5
10
Normal Q-Q Plot
-2
-1
0
1
2
Theoretical Quantiles
Alternativamente si può effettuare un test, noto come il test di Shapiro-Wilk, che saggia l’ipotesi
nulla di normalità distributiva di un insieme di dati:
shapiro.test(residuals(g))
Shapiro-Wilk normality test
data: residuals(g)
W = 0.987, p-value = 0.8524
Il p-value indica che l’ipotesi nulla non si rifiuta e dunque i residui sono normalmente distribuiti.
Se si costruisce un istogramma si osserva infatti la classica forma campanulare:
18
hist(residuals(g),15)
4
3
0
1
2
Frequency
5
6
7
Histogram of residuals(g)
-5
0
5
10
residuals(g)
(si provi a cambiare il valore 15 per vedere cosa succede al grafico).
Misure diagnostiche
Nella libreria faraway sono contenuti alcuni comandi che producono i leverages, i residui
studentizzati e la distanza di cook. Il comando influence si applica all’output di un modello di
regressione e produce una lista al cui interno (sotto il nome di hat) sono contenuti i valori di
leverages:
ginf<-influence(g)
ginf$hat
Australia
Austria
0.06771343
0.12038393
Canada
Chile
0.15840239
0.03729796
Denmark
Ecuador
0.06271782
0.06372651
Greece
Guatamala
0.09662073
0.06049212
Ireland
Italy
0.21223634
0.06651170
Malta
Norway
0.07940290
0.04793213
Panama
Paraguay
0.03897459
0.06937188
South Africa South Rhodesia
0.06510405
0.16080923
Belgium
0.08748248
China
0.07795899
Finland
0.09204246
Honduras
0.06008079
Japan
0.22330989
Netherlands
0.09061400
Peru
0.06504891
Spain
0.07732854
19
Bolivia
0.08947114
Colombia
0.05730171
France
0.13620478
Iceland
0.07049590
Korea
0.06079915
New Zealand
0.05421789
Philippines
0.06425415
Sweden
0.12398898
Brazil
0.06955944
Costa Rica
0.07546780
Germany
0.08735739
India
0.07145213
Luxembourg
0.08634787
Nicaragua
0.05035056
Portugal
0.09714946
Switzerland
0.07359423
Turkey
0.03964224
Zambia
0.06433163
Tunisia United Kingdom
0.07456729
0.11651375
Jamaica
Uruguay
0.14076016
0.09794717
United States
0.33368800
Libya
0.53145676
Venezuela
0.08628365
Malaysia
0.06523300
Questi due comandi producono un grafico dei Leverages in cui si mostrano le etichette dei paesi
con i 5 leverages più alti:
contries<-row.names(savings)
halfnorm(lm.influence(g)$hat,5,labs=contries,ylab="Leverages")
Si provi ancora una volta a modificare il valore 5 per valutarne gli effetti.
Per calcolare i residui studentizzati internamente si usa la loro formula definitoria basata sui valori
di leverages appena stimati:
gs<-summary(g) # mette in gs il summary di g
gs$sig # è la radice quadrata della varianza stimata
3.8027
stud.int<-residuals(g)/(gs$sig*sqrt(1-ginf$hat)) # formula per il calcolo
Invece per ottenere i residui studentizzati esternamente si può utilizzare direttamente la formula:
stud.est<-rstudent(g)
Infine per calcolare la distanza di Cook si utilizza il comando:
cook<-cooks.distance(g)
halfnorm(cook,3,labs=countries,ylab=”Cook’s distances”) # fa il grafico
Un esercizio
Il dataset star (libreria farway) contiene di dati sulla luminosità e sulla temperatura di alcune stelle
del sistema solare. Si vuole valutare se stelle molto luminose corrispondono a stelle con
temperature elevate e viceversa.
data(star)
plot(star$temp,star$light,xlab=”Temperatura”,ylab=”Luminosità”)
g<-lm(light~temp,star)
abline(g)
20
6.0
5.5
5.0
4.0
4.5
Luminosità
3.6
3.8
4.0
4.2
4.4
4.6
Temperatura
in cui si osserva purtroppo un andamento decrescente dovuto molto probabilmente alla presenza
di quattro punti anomali, che corrispondono a quattro stelle aventi una temperatura inferiore a 3.6.
Se si calcolano i leverages infatti si ha che quelli maggiori di 2(m+1)/n sono proprio quei 4 punti:
cbind(influence(g)$hat,star$temp)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
[,1]
0.02220190
0.03734096
0.02191917
0.03734096
0.02130230
0.02705977
0.07805447
0.03865181
0.02191917
0.02220190
0.19410341
0.02497782
0.02870476
0.04440927
0.02137941
0.02438666
0.02292159
0.02438666
0.02292159
0.19410341
0.02137941
0.02137941
0.02438666
0.02960436
0.02253604
0.02438666
0.02137941
0.02253604
0.02335854
[,2]
4.37
4.56
4.26
4.56
4.30
4.46
3.84
4.57
4.26
4.37
3.49
4.43
4.48
4.01
4.29
4.42
4.23
4.42
4.23
3.49
4.29
4.29
4.42
4.49
4.38
4.42
4.29
4.38
4.22
21
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
0.19834440
0.02253604
0.03734096
0.02631438
0.19410341
0.02292159
0.04597716
0.03371684
0.02631438
0.03371684
0.02497782
0.02253604
0.02631438
0.03055537
0.02631438
0.03608151
0.02631438
0.02438666
3.48
4.38
4.56
4.45
3.49
4.23
4.62
4.53
4.45
4.53
4.43
4.38
4.45
4.50
4.45
4.55
4.45
4.42
Dunque si può ristimare un modello di regressione escludendo le stelle con temperatura inferiori a
3.6:
g2<-lm(light~temp,star,subset=(temp>3.6))
abline(g2)
5.0
4.5
4.0
Luminosità
5.5
6.0
da cui si ottiene una relazione crescente fra le due variabili:
3.6
3.8
4.0
4.2
4.4
4.6
Temperatura
22









