UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II
SCUOLA POLITECNICA E DELLE SCIENZE DI BASE
DIPARTIMENTO DI MATEMATICA E APPLICAZIONI
RENATO CACCIOPPOLI
GUIDA DELLO STUDENTE
CORSO DI LAUREA IN MATEMATICA
Classe delle Lauree in Scienze Matematiche, Classe N. L-35
ANNO ACCADEMICO 2016/2017
Napoli, luglio 2016
Finalità del Corso di Studi e sbocchi occupazionali
La matematica e' nota come disciplina caratterizzata da un lato da un rigoroso
impianto teorico-formale che in maniera deduttiva ottiene risultati di notevole complessita'
ed astrazione, e dall'altro da pervasivi e diffusi risvolti applicativi finalizzati alla risoluzione
di problemi concreti in altre discipline. L'obiettivo del corso di studi triennale e' quindi
quello di presentare questo duplice aspetto della matematica offrendo insegnamenti adatti
al raggiungimento di tale obiettivo. Il corso di laurea in Matematica fornisce quindi una
solida preparazione di base in tutti i settori della disciplina, attraverso un unico percorso
formativo con insegnamenti quasi tutti obbligatori, concepito in modo che i laureati in
Matematica siano in grado di affrontare proficuamente gli studi successivi, in particolare il
corso di laurea magistrale in Matematica, e che abbiano la capacità di esprimere
concretamente le conoscenze acquisite nei diversi settori lavorativi in cui potranno essere
coinvolti.
Al trmine del percorso formativo, il laureato in matematica avra’ quindi la capacita`
di fornire dimostrazioni rigorose di risultati matematici anche in maniera originale, la
capacita` di formalizzare matematicamente problemi di moderata difficolta` formulati nel
linguaggio naturale, e di trarre profitto da questa formulazione per chiarirli o risolverli. A
questo scopo sono previsti esami in tutte le aree della matematica per complessivi 118
CFU, il cui superamento prevede prove individuali di varia natura (scritte e/o orali e/o di
laboratorio) sui contenuti dei singoli corsi. Il laureato in matematica avra’ altresi’ la
capacita di comprendere e/o sviluppare semplici modelli matematici formulati nel
linguaggio proprio delle discipline applicative, per esempio di ambito fisico e/o economico,
ed avra’ le competenze per utilizzare strumenti informatici e computazionali come
supporto per attività scientifiche, finanziarie e piu’ in generale dei servizi. A questo scopo
sono previsti esami in tali aree per complessivi 33 CFU, il cui superamento prevede prove
individuali di varia natura (scritte e/o orali e/o di laboratorio) sui contenuti dei singoli corsi.
Il laureato in matematica avra’ infine la capacita di interagire con altre figure professionali
in tutti gli ambiti lavorativi, e di comunicare in pubblico, sia per iscritto che oralmente, in
maniera chiara e ordinata, argomenti di matematica studiati autonomamente su testi ed
articoli scientifici anche redatti in lingua inglese. A questo scopo sono previsti
insegnamenti a scelta libera con cui gli studenti completano la preparazione secondo un
proprio progetto formativo, colloqui di lingua inglese, tirocini presso scuole o aziende, e
una prova finale che prevede la compilazione di un elaborato autonomo.
La maggior parte dei laureati in matematica prosegue gli studi con il corso di laurea
magistrale in matematica. In ogni caso, grazie alla attitudine e alla preparazione al
Problem Solving, i laureati in matematica possono svolgere compiti tecnici e professionali
legati al trattamento quantitativo di dati, anche con strumenti informatici, in vari campi del
settore industriale e dei servizi, come ad esempio gli ambiti informatico, finanziario,
sanitario, della pubblica amministrazione, ingegneristico e piu' in generale in tutti i contesti
ad alto contenuto tecnologico.
Requisiti di accesso
Per l’ammissione al Corso di Laurea, oltre alla capacità logico deduttiva, è richiesta allo
studente la predisposizione al rigore scientifico e la conoscenza di base degli argomenti
delle discipline scientifiche previsti dai programmi delle scuole medie superiori.
Tali conoscenze comprendono:
• conoscenze di base di matematica, comprendenti i fondamenti del calcolo algebrico ed
aritmetico, della trigonometria, della geometria analitica, delle funzioni elementari e dei
logaritmi ;
• conoscenze di base di fisica classica, con riferimento ai fondamenti della meccanica,
dell'ottica e dell'elettromagnetismo;
• conoscenze basilari ed utilizzo dei principali programmi informatici di larga diffusione;
• conoscenze elementari della lingua inglese relativamente ai principi della traduzione e
comprensione di testi scritti semplici.
Inoltre sono richieste:
• la capacità di interpretare il significato di un testo e di sintetizzarlo o di rielaborarlo in
forma scritta ed orale;
• la capacità di risolvere un problema attraverso la corretta individuazione dei dati ed il loro
utilizzo nella forma più efficace;
• la capacità di utilizzare le strutture logiche elementari (ad esempio, il significato di
implicazione, equivalenza, negazione di una frase, ecc.) in un discorso scritto e orale,
• la capacità di valutare criticamente un dato o un'osservazione e di utilizzarli
opportunamente nel loro contesto (es. saper cogliere una evidente incongruenza in una
misura scientifica).
Al fine di valutare l’adeguatezza della preparazione di base e l’attitudine agli studi
di Matematica, il Corso di Studi prevede un test di ammissione obbligatorio.
Informazioni sulle modalità di svolgimento del test e sulle eventuali prescrizioni
conseguenti
al
mancato
superamento
sono
reperibili
sul
sito:
http://www.scuolapsb.unina.it/index.php/studiare-al-napoli/ammissione-ai-corsi.
In
particolare, per gli studenti che non superano il test di ingresso, così come per quelli che
non hanno effettuato il test di ingresso e non godono delle condizioni per l'esonero del
test, e' prevista una prova di recupero nel mese di novembre. Gli studenti che in nessuna
occasione riusciranno a superare e/o sostenere il test, si vedranno attribuire un Obbligo
Formativo Aggiuntivo (OFA) di "Basi di Matematica" che impone di dover sostenere con
esito positivo, prima di tutti gli altri, l'esame di Analisi Matematica 1 previsto al primo anno
di corso. In ogni caso il debito formativo dovra' essere estinto entro il primo anno
Sito Web del Corso di Laurea
www.cs-matematica.unina.it
Referente del Corso di Studi
Coordinatore dei Corsi di Studio in Matematica: prof. Marco Lapegna– Dipartimento di
Matematica e Applicazioni Renato Caccioppoli - tel. 081/675623 - e-mail:
[email protected].
Manifesto degli Studi
Insegnamento o
attività formativa
Modulo
CFU
SSD
Ambiti
Tip.
Disciplin
(*)
ari
Propedeuticità
I Anno (immatricolati 2016-17)
Analisi matematica I
13
MAT/05
1
Geometria
12
MAT/03
1
Algebra
12
MAT/02
1
Laboratorio di
Programmazione
8
INF/01
1
Fisica 1 con laboratorio
10
FIS/01
1
Lingua inglese
5
5
II Anno (immatricolati 2015-16)
Analisi Matematica II
9
MAT/05
2
Geometria II
9
MAT/03
2
Algebra II
6
MAT/02
2
Fisica matematica
12
MAT/07
2
Probabilita’ e statistica
9
MAT/06
2
Laboratorio di
Programmazione e Calcolo
9
MAT/08
2
Fisica 2 con Laboratorio
9
FIS/01
4
Logica e Fondamenti di
Matematica
9
MAT/04-01
2
Geometria 3
6
MAT/03
2
6
MAT/05
2
6
MAT/07
2
Analisi Matematica I
Geometria I
Algebra I
.
Analisi Matematica I
Analisi Matematica I
Laboratorio di
Programmazione,
Analisi Matematica
1, Geometria 1
Fisica I con
Laboratorio
III Anno (immatricolati 2014-15)
Sistemi Dinamici
Sistemi Dinamici
mod.1
mod. 2
A scelta libera (a)
12
Corso di SSD consentito,
scelto nella Tabella A
6
Altre attivita’ formative (b)
6
6
seminario pre laurea
2
6
Prova finale
4
5
3
FIS/01, INF/01,
SECS S/06
4
Algebra I, Geometria
I
Geometria II
Analisi Matematica
II, Fisica Matematica
Analisi Matematica
II, Fisica Matematica
Alcuni insegnamenti del primo e secondo anno sono sdoppiati in gruppi. Appartengono al
primo gruppo gli studenti la cui prima lettera del cognome e’ compresa tra A e I.
Appartengono invece al secondo gruppo gli studenti la cui prima lettera del cognome e’
compresa tra J e Z.
Analisi Matematica I
Geometria I
Algebra I
Fisica 1 con Laboratorio
Geometria II
Laboratorio di Programmazione e Calcolo
Fisica Matematica
Note:
(a) Gli studenti possono scegliere insegnamenti per 12 CFU all’interno della seguente Tabella A, tra gli
insegnamenti della laurea magistrale in matematica o presso altri corsi di laurea dell’ateneo, purche’
coerenti con il percorso formativo (per indicazioni dettagliate, si veda regolamento sul sito web del
corso di laurea)
(b) ulteriori conoscenze linguistiche, nonché abilità informatiche e telematiche, relazionali, o comunque
utili per l'inserimento nel mondo del lavoro, nonché attività formative volte ad agevolare le scelte
professionali, mediante la conoscenza diretta del settore lavorativo cui il titolo di studio può dare
accesso, tra cui, in particolare, i tirocini formativi e di orientamento (per indicazioni dettagliate, si
veda regolamento sul sito web del corso di laurea)
Tabella A: Esami opzionali
Insegnamento o
attività formativa
Teoria di Galois
Modulo
CFU
SSD
Tipologia
(*)
Propedeuticità
Attivato
anno 16-17
6
MAT/02
3
Algebra II
SI
6
MAT/02
3
Geometria I
NO
6
MAT/03
3
Geometria I
NO
6
MAT/03
3
Algebra I; Analisi
Matem I; Geometria I
NO
6
MAT/04
3
Geometria I
SI
6
MAT/05
3
Analisi Matematica II
SI
6
MAT/05
3
Analisi Matematica II
SI
Calcolo delle Probabilità
6
MAT/06
3
Statistica Matematica
6
MAT/06
3
6
MAT/07
3
Fisica Matematica
NO
6
MAT/07
3
Fisica Matematica
NO
6
FIS/01
4
Fisica 2 con
Laboratorio
SI
Elementi di Geometria
Algebrica e Differenz.
Elem. di Topol. Algebr.
e Geom. Combinatoria
Elementi di Didattica
della Matematica
Matematiche
Complementari
Complementi di Analisi
Matematica
Misura e Integrazione
secondo Lebesgue
Elementi di Fisica
Matem. del Continuo
Introd. ai Met. e Modelli
Matematici per Applic.
Preparazione di
esperienze didattiche
Probab. e Statistica,
Analisi Matematica I
Probab. e Statistica,
Analisi Matematica I
SI
SI
Elementi di Fisica
Moderna
Elementi di Economia
Matematica
Laboratorio di
Programmazione 2
6
FIS/01
4
6
SECS
S/06
4
6
INF/01
4
Fisica 2 con
Laboratorio
SI
SI
Laboratorio di
Programmazione
SI
(*) Legenda delle tipologie delle attività formative ai sensi del DM 270/04
Attività
1
2
3
4
5
6
7
formativa
Art. 10
Art. 10
Art. 10
Art. 10
Art. 10
Art. 10
Art. 10
rif.
comma
comma
comma
comma
comma
comma
comma
DM270/04
1, a)
1, b)
5, a)
5, b)
5, c)
5, d)
5, e)
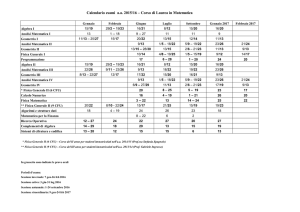
Calendario delle attività didattiche - a.a. 2016/2017
1° periodo didattico
1° periodo di esami
2° periodo didattico
2° periodo di esami
3° periodo di esami
Primo anno
Inizio
20 settembre 2016
27 dicembre 2016
6 febbraio 2017
15 maggio 2017
1 settembre 2017
Termine
22 dicembre 2016
3 febbraio 2017
12 maggio 2017
31 luglio 2017
29 settembre 2017
1° periodo didattico
1° periodo di esami
2° periodo didattico
2° periodo di esami
3° periodo di esami
Secondo e terzo anno
Inizio
20 settembre 2016
27 dicembre 2016
6 marzo 2017
12 giugno 2017
1 settembre 2017
Termine
22 dicembre 2016
3 marzo 2017
9 giugno 2017
31 luglio 2017
29 settembre 2017
E’ consentito sostenere esami anche durante la prima settimana di ciascun periodo didattico in
prosecuzione di appelli regolarmente effettuati durante il periodo di esami precedente
Gli studenti senza obbligo di frequenza possono sostenere esami tutti i mesi, escluso aprile e
agosto, previo accordo con il docente del corso.
Attività formative
Insegnamento: Algebra 1
Modulo Unico
Settore Scientifico - Disciplinare: MAT02
CFU 12:
Obiettivi formativi: Conoscenza critica dei contenuti e dei metodi dell’algebra moderna
Contenuti: Teoria degli insiemi, aritmetica, strutture algebriche fondamentali, teoria dei gruppi
Propedeuticità: Nessuna
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Geometria 1
Modulo Unico
Settore Scientifico - Disciplinare: MAT03
CFU 12:
Obiettivi formativi: Introdurre e formalizzare i concetti fondamentali dell’algebra lineare e della geometria
euclidea: spazi vettoriali, sistemi lineari, matrici e
diagonalizzazione, spazi euclidei, riferimenti e
rappresentazione analitica, luoghi geometrici notevoli (coniche e quadriche)
Contenuti: I concetti fondamentali dell’algebra lineare e della geometria euclidea: spazi vettoriali, sistemi
lineari, matrici e diagonalizzazione, spazi euclidei, riferimenti e rappresentazione analitica, luoghi geometrici
notevoli (coniche e quadriche)
Propedeuticità: Nessuna
Modalità di accertamento del profitto: Superamento di una prova scritta e di una prova orale
Insegnamento: Analisi Matematica 1
Modulo Unico
Settore Scientifico - Disciplinare: MAT05
CFU 13:
Obiettivi
formativi:
Obiettivo
del
corso
è
di
introdurre
e
formalizzare
fondamentali dell'Analisi Matematica, del calcolo differenziale e del calcolo integrale.
i
concetti
Contenuti: Numeri reali, limiti, continuità per le funzioni reali di una variabile reale,
calcolo differenziale, formula di Taylor ed applicazioni, concetto di area, integrali per
le funzioni di una variabile reale.
Propedeuticità: Nessuna
Modalità di accertamento del profitto: Superamento di una prova scritta e di una prova orale
Insegnamento: Probabilità e Statistica
Modulo Unico
Settore Scientifico - Disciplinare: MAT06
CFU 9
Obiettivi formativi: L’insegnamento si propone di presentare gli elementi di base della Probabilità sia con
riferimento ai loro aspetti concettuali e teorici che ai loro collegamenti con le applicazioni. In particolare, si
sottolinea l’intenzione di rendere consapevole lo studente del fatto che gli assiomi alla base del calcolo delle
probabilità formalizzano alcune idee-forza e che essi sono il risultato di un percorso scientifico e culturale con
contributi da diversi ambiti sviluppatosi nell’arco temporale di alcune decadi. Inoltre, si pone particolare enfasi
al tentativo di far coglier agli studenti l’importanza che strumenti propri dell’analisi matematica, dell’algebra e
della logica assumono nella determinazione dei risultati e nella coerenza dell’impianto assiomatico. I
contenuti e i metodi della Statistica inferenziale, oltre a completare una formazione iniziale nel contesto
disciplinare, saranno utili a mostrare l’applicazione di alcuni risultati ottenuti in ambito probabilistico.
Contenuti: I contenuti includono la definizione di spazio di probabilità e la presentazione di alcune
proposizioni da esso deducibili, il concetto di variabile aleatoria e della relativa distribuzione, alcune notevoli
distribuzioni di probabilità, momenti, cenni al caso multidimensionale, risultati asintotici, rappresentazioni dei
dati, stima di parametri, introduzione ai test di ipotesi.
Propedeuticità: Analisi Matematica 1
Modalità di accertamento del profitto: Superamento di una prova orale nella cui parte iniziale sarà
proposta la risoluzione di un esercizio.
Insegnamento: Laboratorio di Programmazione
Modulo Unico
Settore Scientifico - Disciplinare: INF01
CFU 8:
Obiettivi formativi: Il corso intende fornire una introduzione alle metodologie di progetto, sviluppo ed analisi
di algoritmi nonchè all’uso dei principali strumenti di calcolo (hardware e software) con particolare riguardo
alla influenza che questi ultimi esercitano sullo sviluppo degli algoritmi stessi. Parte integrante del corso è
l’attività di laboratorio.
Contenuti: Il concetto di algoritmo e la macchina di Von Neumann, la rappresentazione dei dati e delle
istruzioni, le strutture dati e di controllo per lo sviluppo di algoritmi, i principali algoritmi non numerici
(ordinamento, ricerche, merging e operazioni di base con matrici e vettori) la complessità computazionale,
l’aritmetica floating point, cenni alla stabilità degli algoritmi e ai criteri di arresto. Strumenti software di base
per il calcolo scientifico ( sistemi operativi con particolare riguardo a Unix, Fortran 90)
Propedeuticità: Nessuna
Modalità di accertamento del profitto: Prova di laboratorio e/o prova orale
Insegnamento: Fisica 1 con Laboratorio
Modulo Unico
Settore Scientifico - Disciplinare: FIS01
CFU 10:
Obiettivi formativi: Acquisizione di competenze metodologiche e disciplinari su contenuti di Meccanica
classica, Termodinamica ed elementi di Fisica Moderna
Contenuti: Meccanica classica, Termodinamica ed elementi di Fisica Moderna
Propedeuticità: Nessuna
Modalità di accertamento del profitto: Superamento di una prova scritta e di una prova orale
Insegnamento: Algebra 2
Modulo Unico
Settore Scientifico - Disciplinare: MAT02
CFU 6 :
Obiettivi formativi: Conoscenza critica dei contenuti e dei metodi dell’algebra moderna.
Contenuti: Teoria degli anelli, anelli di polinomi, teoria dei campi, cenni alla teoria di Galois
Propedeuticità: Algebra 1
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Geometria 2
Modulo Unico
Settore Scientifico - Disciplinare: MAT03
CFU 9
Obiettivi formativi: Introdurre allo studio degli spazi a più dimensioni. Studio di quadriche reali, curve e
superfici. Studio delle strutture topologiche e metriche, delle funzioni che conservano tali strutture,
connessione e compattezza
Contenuti: Studio degli spazi a più dimensioni. Studio di quadriche reali, curve e superfici. Studio delle
strutture topologiche e metriche, delle funzioni che conservano tali strutture, connessione e compattezza
Propedeuticità: Geometria 1
Modalità di accertamento del profitto: Superamento di una prova scritta e di una prova orale
Insegnamento: Analisi Matematica 2
Modulo Unico
Settore Scientifico - Disciplinare: MAT05
CFU 9 :
Obiettivi formativi: Il corso offre approfondimenti sul calcolo differenziale, riferito ad applicazioni tra spazi
euclidei, e sul calcolo integrale per funzioni di più variabili..
Contenuti: Calcolo differenziale per applicazioni tra spazi euclidei; curve e superfici; forme differenziali;
funzioni e sistemi di funzioni implicite. Integrazione multipla. Serie di potenze.
Propedeuticità: Analisi Matematica 1
Modalità di accertamento del profitto: Superamento di una prova scritta e di una prova orale
Insegnamento: Fisica Matematica
Modulo Unico
Settore Scientifico - Disciplinare: MAT07
CFU 12 :
Obiettivi formativi: L’obiettivo del corso è quello di introdurre (per gli studenti della laurea triennale in
Matematica) le strutture matematiche elementari che sono intrinseche alla dinamica classica, sia nella loro
formulazione geometrica globale (dopo Newton e D’Alembert), sia nella loro versione analitica locale (dopo
Lagrange ed Hamilton). Lo scopo è quello di mostrare la dinamica classica come una sorgente rilevante della
matematica teorica così come un’area paradigmatica della matematica applicata.
Contenuti:
Calcolo differenziale ed equazioni differenziali negli spazi euclidei. Meccanica Newtoniana, Lagrangiana ed
Hamiltoniana. Applicazioni alla dinamica celeste e terrestre.
Propedeuticità: Analisi Matematica 1
Modalità di accertamento del profitto: Superamento di una prova scritta e orale
Insegnamento: Laboratorio di Programmazione e Calcolo
Modulo Unico
Settore Scientifico - Disciplinare: MAT08
CFU 9:
Obiettivi formativi: Il corso intende fornire una introduzione alle metodologie di progetto, sviluppo ed analisi
dei metodi e degli algoritmi della matematica numerica. Parte integrante del corso e’ l’attività di laboratorio.
Contenuti:
L’analisi dell’errore di round-off degli algoritmi, analisi della stabilità degli algoritmi, il
condizionamento. Calcolo matriciale: algoritmi di Gauss e di Cholesky. Interpolazione polinomiale.
Interpolazione mediante spline; approssimazione di dati discreti con il metodo dei minimi quadrati, la
quadratura: formule elementari ed algoritmi adattativi; risoluzione di equazioni non lineari: metodi elementari
e ibridi; Metodi iterativi per equazioni lineari: Jacobi e Gauss Siedel; risoluzione di ODE: metodi elementari.
Lo sviluppo di software matematico.
Propedeuticità: Laboratorio di Programmazione, Analisi matematica 1, Geometria 1
Modalità di accertamento del profitto: Prova di laboratorio e/o prova orale
Insegnamento: Fisica 2 con Laboratorio
Modulo Unico
Settore Scientifico - Disciplinare: FIS01
CFU 9:
Obiettivi formativi: Acquisizione di competenze metodologiche e disciplinari
Elettromagnetismo, Ottica, ed elementi di Fisica Moderna
Contenuti: Elettromagnetismo, Ottica, ed elementi di Fisica Moderna
Propedeuticità: Fisica 1 con Laboratorio
sui
contenuti
di
Modalità di accertamento del profitto: Superamento di una prova scritta e di una prova orale
Insegnamento: Logica e Fondamenti di Matematica
Modulo Unico
Settore Scientifico - Disciplinare: MAT01 e MAT04
CFU 9 :
Obiettivi formativi: Acquisizione di una visione storico - critica delle teorie e dei metodi della matematica.
Teoria “ingenua” ed elementi di teoria assiomatica degli insiemi. La nozione di infinito. Ordinali e cardinali.
Concetti fondamentali della logica classica, ruolo della logica nella matematica e rapporti con la lingua
naturale.
Contenuti: Dalla teoria ingenua degli insiemi alla crisi dei fondamenti, alla teoria assiomatica. Gli assiomi
della teoria ZF. Numeri ordinali e cardinali. Costruzione dei numeri naturali come ordinali finiti e come
elementi di una terna di Peano. Induzione e ricorrenza sui naturali e sugli ordinali. Insiemi finiti e infiniti e
problematica storico-epistemologica dell'infinito. Costruzione dei sistemi numerici N, Z, Q, R. L'assioma della
scelta. L'assioma di fondazione e l'universo U degli insiemi. Cenni ad alcuni sviluppi più recenti. Concetti e
risultati fondamentali della logica classica delle proposizioni e dei predicati: linguaggio formale,
sintassi/semantica, dimostrazioni, modelli, ecc.
Propedeuticità: Algebra 1; Geometria 1
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Geometria 3
Modulo Unico
Settore Scientifico - Disciplinare: MAT03
CFU 6
Obiettivi formativi: Il corso si propone di sviluppare la conoscenza critica delle curve e superfici da un punto
di vista algebrico e differenziale
Contenuti: Curve e superfici, con particolare riferimento a quelle immerse nello spazio ordinario, da un
punto di vista algebrico e differenziale
Propedeuticità:
Geometria 2
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Sistemi Dinamici (mod.1)
Modulo 1
Settore Scientifico - Disciplinare: MAT05
CFU 6
Obiettivi formativi: : Acquistare padronanza delle principali tecniche analitiche per lo studio delle equazioni
differenziali ordinarie. Diffeomorfismi tra spazi euclidei. Fondamentali nozioni di analisi complessa. Studio di
fenomeni evolutivi delle Scienze Applicate tramite l’uso di sistemi dinamici.
Contenuti: Il teorema delle funzioni implicite e della funzione inversa con applicazioni in particolare allo
studio delle superfici. Cenni sulle funzioni olomorfe e funzioni analitiche, equazioni di Cauchy-Riemann,
teoremi di Cauchy. Equazioni differenziali ordinarie. Teoremi di esistenza e unicità locale e globale.
Classificazione dei punti critici di un sistema di ODE lineari 2x2.
Propedeuticità: Analisi Matematica 2; Fisica Matematica
Modalità di accertamento del profitto: Superamento di un esame integrato, eventualmente articolato in
piu’ prove, sui contenuti di Sistemi Dinamici (mod.1) e Sistemi Dinamici (mod.2)
Insegnamento: Sistemi Dinamici (mod.2)
Modulo 2
Settore Scientifico - Disciplinare: MAT07
CFU 6 :
Obiettivi formativi: : Acquistare padronanza delle principali tecniche analitiche per lo studio delle equazioni
differenziali ordinarie. Diffeomorfismi tra spazi euclidei. Fondamentali nozioni di analisi complessa. Studio di
fenomeni evolutivi delle Scienze Applicate tramite l’uso di sistemi dinamici.
Contenuti: Metodo diretto ed indiretto di Liapunov. Teoremi di stabilità e di instabilità. Teorema della varietà
centrale. Cenni di teoria della biforcazione. Analisi qualitativa delle soluzioni con particolare riferimento al loro
comportamento asintotico nel tempo. Teorema di Poincaré-Bendixon.
Propedeuticità: Analisi Matematica 2; Fisica Matematica
Modalità di accertamento del profitto: Superamento di un esame integrato, eventualmente articolato in
piu’ prove, sui contenuti di Sistemi Dinamici (mod.1) e Sistemi Dinamici (mod.2)
Insegnamento: Teoria di Galois
Modulo Unico
Settore Scientifico - Disciplinare: MAT02
CFU 6 :
Obiettivi formativi: Conoscenza critica dei contenuti e dei metodi dell’algebra moderna:
Contenuti: teoria dei campi, gruppi di Galois, risolubilità per radicali.
Propedeuticità: Algebra 2
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Elementi di geometria algebrica e differenziale
Modulo Unico
Settore Scientifico - Disciplinare: MAT03
CFU 6 :
Obiettivi formativi: Introduzione alle varietà algebriche e differenziabili
Contenuti: Introduzione alle varietà algebriche e differenziabili
Propedeuticità: Geometria 1
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Elementi di topologia algebrica e geometria combinatoria
Modulo Unico
Settore Scientifico - Disciplinare: MAT03
CFU 6 :
Obiettivi formativi: Varietà topologiche. Superfici e loro classificazione. Strutture geometriche in spazi
proiettivi su campi finiti.
Contenuti: Varietà topologiche. Superfici e loro classificazione. Strutture geometriche in spazi proiettivi su
campi finiti.
Propedeuticità: Geometria 1
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Elementi di Didattica della Matematica
Modulo Unico
Settore Scientifico - Disciplinare: MAT04
CFU 6 :
Obiettivi formativi: Introduzione alle problematiche dell'apprendimento della matematica e alle principali
teorie cognitive. Confronto tra la sistemazione deduttiva delle teorie matematiche e i processi euristici della
scoperta. Problem solving e problem posing. La metacognizione. Il laboratorio, che affianca il corso, e’
costituito da attività mirate sopratutto a prendere coscienza del proprio processo di apprendimento e di
comprensione.
Contenuti: Nel corso che ha carattere interattivo, si affrontano problematiche legate all'apprendimento della
matematica, a partire dai contenuti disciplinari già posseduti dagli studenti e dalle modalita’ di studio da essi
sperimentate. Gli approfondimenti riguardano nozioni di particolare rilievo (ad esempio il limite, l'infinito), le
procedure e il linguaggio dell'algebra, il metodo matematico (ad esempio, come si costruisce una
dimostrazione), il problem solving, ecc.
Propedeuticità: Algebra 1; Analisi Matematica 1; Geometria 1
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Matematiche Complementari
Modulo Unico
Settore Scientifico - Disciplinare: MAT04
CFU 6 :
Obiettivi formativi: I fondamenti del metodo assiomatico in geometria. Panorama dei principali filoni di studio
della geometria, con particolare riguardo alle geometrie non euclidee.
Contenuti: Aspetti fondazionali della geometria: l'impostazione assiomatica da Euclide a Hilbert. Fondazione
assiomatica
della
geometria
euclidea
del
piano
e
dello
spazio.
Il
problema
della
completezza/continuità/categoricità. Retta euclidea e numeri reali. L'assioma delle parallele e la sua storia. Le
geometrie non euclidee. Geometria iperbolica del piano. Inversioni circolari e birapporti. Il modello di
Poincare’. La geometria ellittica e la geometria sferica.
Propedeuticità: Geometria 1
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Complementi di Analisi Matematica
Modulo Unico
Settore Scientifico - Disciplinare: MAT05
CFU 6 :
Obiettivi formativi: Introduzione alla variabile complessa; funzioni armoniche; cenni sulle serie di Fourier ed
applicazioni alle equazioni a derivate parziali.
Contenuti: Introduzione alla variabile complessa; funzioni armoniche; cenni sulle serie di Fourier ed
applicazioni alle equazioni a derivate parziali.
Propedeuticità: Analisi Matematica 2
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Misura ed Integrazione secondo Lebesgue
Modulo Unico
Settore Scientifico - Disciplinare: MAT05
CFU 6 :
Obiettivi formativi: Obiettivo del corso è introdurre la teoria della misura e dell’integrazione secondo
k
Lebesgue in R e fornire semplici applicazioni.
k
Contenuti: Introduzione della teoria della misura e dell’integrazione secondo Lebesgue in R ed applicazioni.
Propedeuticità: Analisi Matematica 2
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Calcolo delle Probabilita’
Modulo Unico
Settore Scientifico - Disciplinare: MAT06
CFU 6 :
Obiettivi formativi: Considerare gli elementi fondamentali di teoria della misura nel contesto probabilistico e
presentare alcuni degli arricchimenti che in tale ambito sono stati determinati.
Contenuti: Teoremi di unicità ed estensione. La misura di Lebesgue. Il completamento di uno spazio di
probabilità. Variabile aleatoria e funzioni misurabili. Distribuzioni congiunte. Il concetto di indi-pendenza
stocastica e Leggi 0-1. Integrazione di funzioni misurabili e momenti. Disuguaglianze notevoli (di Markov, di
Jensen, di Schwarz, di Hölder, di Chebyshev)e interpretazione mediante i momenti. Indipendenza e misura
prodotto. Estensione n-dimensionale. Aspettazione condizionata rispetto a sigma-algebre.
Propedeuticità: Probabilità e Statistica; Analisi Matematica 1
Modalità di accertamento del profitto: Superamento di una prova orale includente la risoluzione di un
esercizio
Insegnamento: Statistica Matematica
Modulo Unico
Settore Scientifico - Disciplinare: MAT06
CFU 6 :
Obiettivi formativi: Oltre a rivisitare alcuni contenuti già presentati nel corso di base e a presentarne
ulteriori, l’impostazione dell’insegnamento mira ad ottemperare a esigenze di rigore matematico e al
contempo mira a far cogliere la concretezza nella genesi e nelle applicazioni attraverso un esplicito e
costante riferimento ad istanze specifiche, sia pure opportunamente schematizzate..
Contenuti: Campioni casuali. Campioni da popolazioni normali. Momenti campionari. Statistiche d’ordine.
Stimatori: proprietà e metodi di costruzione. Stima intervallare. Regione critica, errori di I e II tipo, ampiezza e
potenza di un test. Test semplicemente più potenti. Metodo del rapporto di verosi-miglianze. Test chiquadrato, test per il confronto di più di due proporzioni, test per le tabelle di contingenza. Metodo di
approssimazione ai minimi quadrati. Regressione.
Propedeuticità: Probabilità e Statistica; Analisi Matematica 1
Modalità di accertamento del profitto: Superamento di una prova orale includente la risoluzione di un
esercizio
Insegnamento: Elementi di Fisica Matematica del Continuo
Modulo Unico
Settore Scientifico - Disciplinare: MAT07
CFU 6 :
Obiettivi formativi: Il corso si propone di fornire gli elementi per lo studio sia cinematico che dinamico della
modellizzazione macroscopica dei sistemi materiali
Contenuti: Studio cinematico e dinamico della modellizzazione macroscopica dei sistemi materiali
Propedeuticità: Fisica Matematica
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Introduzione ai Metodi e Modelli Matematici per le Applicazioni
Modulo Unico
Settore Scientifico - Disciplinare: MAT07
CFU 6 :
Obiettivi formativi: L’obiettivo formativo è quello di presentare modellizzazioni matematiche di
fenomenologie reali attraverso equazioni alle differenze, differenziali ordinarie e/o alle derivate parziali
fornendo le tecniche ed i metodi necessari per il loro studio.
Contenuti: Modellizzazioni matematiche di fenomenologie reali attraverso equazioni alle differenze,
differenziali ordinarie e/o alle derivate parziali, tecniche e metodi necessari per il loro studio.
Propedeuticità: Fisica Matematica
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Preparazione di esperienze didattiche
Modulo Unico
Settore Scientifico - Disciplinare: FIS01-FIS08
CFU 6 :
Obiettivi formativi: Fornire ai futuri insegnanti una panoramica di base su metodi sperimentali della fisica
con enfasi su esperimenti didattici da proporre in aula.
Contenuti: 1. difficoltà di apprendimento, 2. approcci laboratoriali inquiry- e context-based, 3. conflitto
cognitivo e ciclo previsione-esperimento-confronto 4. modellizzazione
1. Esperimenti con sensori connessi al calcolatore su argomenti di cinematica e dinamica: moto rettilineo
uniforme, moto accelerato, moto armonico, principi di Newton, conservazione della quantità di moto e
dell'energia.
2. Richiami e semplici esperimenti su termologia e termodinamica: scambi termici, calore specifico
3. Esperimenti su circuiti elettrici in corrente continua: corrente elettrica, potenziale, circuiti serie/parallelo
4. Ottica geometrica e ottica ondulatoria: leggi di rifrazione e riflessione, diffrazione
5. Fisica moderna: approccio e formalismo alla Dirac
6. Natura della scienza e dell'indagine scientifica.
Propedeuticità: Fisica 2 con Laboratorio
Modalità di accertamento del profitto: Superamento di una prova orale e di un’eventuale prova di
laboratorio
Insegnamento: Elementi di Fisica Moderna
Modulo Unico
Settore Scientifico - Disciplinare: FIS01-FIS08
CFU 6 :
Obiettivi formativi: Acquisizione di competenze metodologiche e disciplinari su contenuti di Fisica Moderna,
con enfasi sulla transizione dalla Meccanica Classica alla Meccanica Relativistica e Quantistica, la fisica
atomica, la fisica nucleare e la fisica dello stato solido
Contenuti: Acquisizione di competenze metodologiche e disciplinari su contenuti di Fisica Moderna, con
enfasi sulla transizione dalla Meccanica Classica alla Meccanica Relativistica e Quantistica, la fisica atomica,
la fisica nucleare e la fisica dello stato solido
Propedeuticità: Fisica 2 con Laboratorio
Modalità di accertamento del profitto: Superamento di una prova orale e di un’eventuale prova di
laboratorio
Insegnamento: Elementi di Economia Matematica
Modulo Unico
Settore Scientifico - Disciplinare: SECS-S/06
CFU 6 :
Obiettivi formativi: L’insegnamento intende far acquisire gli elementi fondanti dei principali modelli
economici come esempio di possibile applicazione della matematica.
Contenuti: Scelte e preferenze, equilibrio economico, aste, scelte di investimento in condizioni di incertezza.
Propedeuticità: Nessuna
Modalità di accertamento del profitto: Superamento di una prova orale
Insegnamento: Laboratorio di Programmazione 2
Modulo Unico
Settore Scientifico - Disciplinare: INF01
CFU 6 :
Obiettivi formativi: L’insegnamento intende fornire un approfondimento delle metodologie di progetto,
sviluppo ed analisi di algoritmi con particolare riguardo a quelli che fanno uso della ricorsione e delle
strutture dati dinamiche, nonchè una introduzione alla struttura e funzioni dei moderni sistemi operativi.
Contenuti: Algoritmi ricorsivi, strutture dati dinamiche: liste, pile, code. Struttura e funzioni dei moderni
sistemi operativi, la gestione dei processi, della memoria e del file system.
Propedeuticità: Laboratorio di programmazione
Modalità di accertamento del profitto: Superamento di una prova orale