UNIVERSITÀ DEGLI STUDI DI NAPOLI
“FEDERICO II”
FACOLTÀ DI SCIENZE MM.FF.NN.
CORSO DI LAUREA MAGISTRALE IN FISICA
CURRICULUM: SPERIMENTALE
ORIENTAMENTO: SUBNUCLEARE E ASTROPARTICELLARE
TESINA DI ELETTRODINAMICA CLASSICA
EFFETTO CHERENKOV E FISICA DELLE
ALTE ENERGIE: ILC (INTERNATIONAL
LINEAR COLLIDER)
PROFESSORE:
STUDENTE:
Salvatore Solimeno
Luigi Marchese - Matr. N94/97
ANNO ACCADEMICO 2010/2011
“Oggi, più che mai, le persone colte hanno il dovere di seminare dubbi, non di
raccogliere certezze”
Norberto Bobbio
2
Indice
Introduzione......................................................................................................4
Capitolo 1
Effetto Cherenkov.............................................................................................5
...1.1 Introduzione e Cenni storici..........................................................................5
...1.2 Fenomenologia dell’effetto Cherenkov...........................................................9
...1.3 Aspetti Microscopici e Macroscopici............................................................12
...1.4 La Teoria di Tamm e Frank..........................................................................13
...1.5 Effetto Cherenkov nel riferimento proprio....................................................19
...1.6 Relazioni costitutive....................................................................................21
.......1.6.1 Introduzione.........................................................................................21
.......1.6.2 Proprietà Strutturali............................................................................23
.......1.6.3 Proprietà di Simmetria.........................................................................26
...1.7 Radiazione Cherenkov dal punto di vista quantomeccanico..........................29
...1.8 Soglia della radiazione Cherenkov................................................................30
...1.9 Intensità della radiazione Cherenkov e distribuzione spettrale......................31
Capitolo 2
Rivelatori Cherenkov......................................................................................33
...2.1 Caratteristiche generali................................................................................33
...2.2 Contatori ad effetto Cherenkov....................................................................34
...2.3 Contatori a soglia.........................................................................................35
...2.4 Contatori differenziali..................................................................................36
Capitolo 3
Rivelatori Cherenkov e Fisica delle Alte Energie: ILC..............................38
...3.1 Introduzione ................................................................................................38
...3.2 I Progetti e la Struttura ...............................................................................40
...3.3 Il 4th Concept ..............................................................................................45
...3.4 Calorimetri a Readout multiplo....................................................................47
.......3.4.1 Il Calorimetro adronico (HCAL)............................................................48
.......3.4.2 Il Calorimetro Elettromagnetico (ECAL)...............................................48
Capitolo 4
Calorimetro a Compensazione........................................................................49
...4.1 Introduzione .................................................................................................49
...4.2 Difficoltà e caratteristiche .............................................................................49
...4.3 Calorimetro DREAM ....................................................................................52
...4.4 Risoluzione energetica adronica .....................................................................55
...4.5 Risoluzione energetica elettromagnetica ........................................................62
Conclusioni..........................................................................................................64
Bibliografia..........................................................................................................65
3
Introduzione
Questa tesina vuole essere uno studio dell’effetto Cherenkov con
una particolare attenzione alle sue applicazioni nell’ambito della
fisica delle Alte Energie. Era necessario scegliere un determinato
esperimento per studiarne, seppur per sommi capi, le possibili applicazione dell’effetto Cherenkov. La scelta è ricaduta su ILC, il
nuovo acceleratore lineare tuttora in fase di progetto, che sarà il
futuro erede di LHC. Si è deciso in questo modo, perchè si è intesa questa tesina come uno spunto per approfondire e allargare le
proprie conoscenze sugli acceleratori che costituiranno il futuro di
LHC e dunque dello scrivente. Il lavoro è stato suddiviso in quattro
capitoli. Doveroso è il rinoscimento nei confronti del lavoro di tesi
di Vito di Benedetto, “Study of a Compensating Calorimeter for a
e+ e− Linear Collider at Very High Energy” per tutto lo sviluppo
della parte sperimentale - applicativa.
Nel Capitolo 1 è sviluppata la teoria dell’effetto Cherenkov. In
primo luogo sono sviluppati gli avvenimenti storici che condussero
Cherenkov a suddetta scoperta. Segue una trattazione dell’effetto
Cherenkov da un punto di vista più strettamente fenomenologico,
con riferimenti ad un punto di vista macroscopico e microscopico. Inoltre è presentato il modello teorico proposto da Tamm e
Frank con alcuni riferimenti alle relazioni costitutive che legano i
vari campi.
Nel Capitolo 2 è invece trattato per sommi capi il principio di
funzionamento dei rivelatori Cherenkov impiegati nella fisica delle
Alte Energie. Sono messi in rilievo i contatori a soglia e quelli differenziali.
Nel Capitolo 3 è invece mostrato in maniera sintetica, ma esaustiva il progetto di ILC (International Linear Collider). In particolare
sono evidenziati i vari progetti proposti, naturalizzati come “Concept” nell’ambiente scientifico. E’ stato riservato un intero paragrafo
al 4th Concept, essendo questo il progetto analizzato in dettaglio nel
successivo capitolo.
Nel Capitolo 4 è discusso il modulo DREAM che è alla base del
Calorimetro a Compensazione che il 4th Concept prevede di implementare in ILC. In particolare è trattata la risoluzione energetica
visto che in questo prototipo si ha la possibilità di determinarla
scindendo i due effetti, quello Cherenkov e quello di scintillazione.
4
Capitolo 1
Effetto Cherenkov
1.1 Introduzione e cenni storici
La storia dell’effetto Cherenkov inizia un po’ prima dell’ufficiale
scoperta per mano dell’omonimo fisico russo. Negli anni 1926 - 1929
il radiochimico francese Mallet pubblicò tre articoli sullo spettro
di luminescenza prodotto da alcuni liquidi organici puri e determinati materiali solidi se eccitati da raggi gamma. Gli spettri osservati
risultavano continui con la regione di piccola lunghezza d’onda dominante. Tutto ciò suggeriva a Mallet che la radiazione osservata non
poteva essere attribuibile alla luminescenza. Mallet non approfondì
questa singolare osservazione e dunque ciò non condusse alla scoperta di un nuovo tipo di radiazione.
Nel 1934 Cherenkov, giovane dottorando russo di Vavilov, stava
studiando la luminescenza di alcune soluzioni di sale di uranile eccitate da raggi gamma provenienti da una sorgente radio quando
osservò un singolare e sconosciuto fenomeno. L’acido solforico puro
posto in un crogiolo di platino vicino alla sorgente radio emetteva
una debole radiazione blue. Cherenkov fu così affascinato da questa
nuova radiazione da decidere di condurre molti altri accurati esperimenti nei successivi quattro anni al fine di investigare le proprietà della radiazione appena scoperta. Irradiò molte sostanze
pure con raggi gamma provenienti da una sorgente radio e tutti
emettevano una debole luce visibile. La sua analisi fu molte dettagliata: studò in dettaglio lo spettro della radiazione, la sua vita
media, lo stato di polarizzazione nonché il ruolo della sorgente di
raggi gamma. Nel 1928 due fisici indiani, Venkateswaran e Karl,
avevano scoperto la radiazione blue irragiando sostanze pure con
luce ultravioletta. Essi avevano interpretato il fenomeno come un
nuovo tipo di luce di scattering. Tuttavia, Vavilov e Tumerman,
qualche anno dopo avevano investigato gli effetti di questo nuovo
nuovo fenomeno scoprendo che in realtà si trattava di ordinaria
luminescenza. La radiazione blue proveniente dall’acqua poteva
subire quenching sia riscaldando l’acqua che aggiungendo ioduro
5
di potassio e inoltre aveva una costante di tempo pari a τ = 1.9 ·
10−9 s. Successivamente fu chiarito che la radiazione blue appena
scoperta era principalmente dovuta alla fluorescenza di piccole impurità organiche che il liquido assorbiva dall’aria. La comunità
scientifica era dunque molto scettica nel riconoscere la radiazione
Cherenkov come di un nuovo tipo, visto la recente smentita. Al fine
di chiarire la differenza fra la nuova radiazione e la comune fluorescenza, Cherenkov ne misurò l’intensità a partire da campioni di
acqua di differenti gradi di purezza. La radiazione risultò scorrelata alle impurità presenti in acqua. Gli esperimenti che fecero luce
sulla natura della nuova radiazione furono esperimenti di quenching e misure delle proprietà di polarizzazione. Cherenkov dimostrò
che la nuova radiazione non era influenzata da agenti di quenching
attivi, quali nitrato d’argento, ioduro di potassio etc...anche se le
loro concentrazioni variavano di un fattore 100. Inoltre, al contrario
dell’ordinaria luminescenza, la nuova radiazione non era influenzata
dal riscaldmento della soluzione. Misure realizzate a partire da diversi liquidi evidenziarono che la radiazione è fortemente polarizzata. Il massimo di polarizzazione era 21.4% e non era influenzato
dal riscaldamento della soluzione, a differenza della forte dipendenza
dalla temperatura della polarizzazione di luminescenza. La scoperta
più inaspettata fu tuttavia l’allineamento dl vettore campo elettrico
della radiazione con la direzione dei raggi gamma incidenti. Per
rendere conto della differenza, basta pensare che in soluzioni luminescenti, come quelle di nitrati di uranile in acqua, la polarizzazione
stimata era inferiore al 1-3%. Inoltre Cherenkov mostrò che la radiazione era eccitata solo dai raggi gamma più energetici, mentre
non risentiva di quelli meno energetici. In altre parole la radiazione
sembrava mostrare un comportamento a soglia. Infatti la radiazione
fu osservata in diversi liquidi ( olio di paraffina, acetone etc...) anche se eccitati da raggi gamma soft, ma subiva quenching in tutti
questi casi semplicemente riscaldando la soluzione e risultava essere
dunque ordinaria luminescenza.
Sulla base dei risultati sperimentali di Cherenkov, Vavilov concluse che suddetta radiazione non poteva essere un nuovo tipo di
luminescenza. Vavilov provò a dare anche una spiegazione circa la
causa di questa nuova radiazione: il bremsstrahlung degli elettroni
Compton allorquando scagliati contro gli atomi di liquido per mezzo
della radiazione gamma. I suggerimenti di vavilov furono subito ac6
colti da Cherenkov che effettuò delle misure in un campo magnetico.
Suddetti esperimenti mostrarono come la radiazione era effettivamente causata dagli elettroni Compton. In aggiunta l’esperimento
mostrò una forte asimmetria della radiazione: nei liquidi la radiazione è emessa principalmente lungo la direzione del fascio gamma
incidente. Tuttavia, i tentativi di spiegare la radiazione Cherenkov
come parte della radiazione di bremsstrahlung degli elettroni Compton anche nella regione del visibile furono poco soddisfacenti, soprattutto perchè l’intensità osservata risultava molto più grande di quella
teorica prevista dalla radiazione di bremsstrahlung nella regione del
visibile.
Così prima dello sviluppo della teoria della radiazione Cherenkov
dovuta a Tamm e Frank, Cherenkov e Vavilov stabilirono le seguenti
proprietà di questa nuova radiazione:
1.
la radiazione è prodotta in tutti i liquidi puri e i solidi trasparenti;
2.
lo spettro è continuo per tutte le sostanze idagate e si estende
o
per l’acqua sotto ai 2200 A;
3.
l’intensità è concentrata principalmente nella regione blue-viola
dello spettro;
4.
la costante di tempo della radiazione è τ = 10−11 s e dunque
non può trattarsi di luminescenza;
5.
la radiazione è eccitata solo dai raggi gamma hard;
6.
la radiazione è fortemente polarizzata, ma la polarizzazione ha
differenti proprietà da quelle della luminescenza;
7.
la radiazione non è causata direttamente dai raggi gamma provenienti dalla sorgente radio, ma è causata dagli elettroni Compton ad alta velocità creati dall’interazione fra i raggi gamma
incidenti e gli elettroni atomici del materiale irradiato;
8.
la radiazione è fortemente asimmetrica ed è diretta lungo la
direzione degli elettroni Compton;
9.
le proprietà della radiazione eccitata dai raggi gamma o dagli
elettroni sono identiche;
7
10.
la nuova radiazione non è riconducibile a nessuna precedentemente studiata.
Dopo questa serie di osservazioni fenomenologiche iniziò una vera
sfida fra i maggiori esperti di Elettrodinamica del tempo per inquadrare in un modello teorico consistente l’effetto appena scoperto.
Era ben chiara la portata innovativa di questa nuova radiazione, a tal
punto che Mallet rivendicò la paternità della scoperta, sostenendo
che Cherenkov, a parte lo studio di polarizzazione, non avesse aggiunto nulla di nuovo ai suoi risultati. Tuttavia la profondità degli
studi condotti da Cherenkov mostrarono come le pretese di Mallet
non fossero sostenute dai fatti.
Nel 1937 Tamm e Frank, basandosi sull’Elettrodinamica classica, svilupparono una teoria perfettamente capace di spiegare le
proprietà dell’effetto appena scoperto e capace di predirre nuove
proprietà e relazioni. La conclusione principale della loro teoria
fu che un elettrone (o qualsiasi particella carica) in moto in un
mezzo trasparente con velocità costante e maggiore della velocità
della luce in quel mezzo emette radiazione in una ben definita direzione. I detrattori della teoria muovevano due obiezioni: la prima
era sostanzialmente la comune assunzione in elettrodinamica secondo cui solo una particella carica accelerata irragia. Frank e Tamm
verificarono come ciò fosse vero solo nel vuoto. La seconda era più
che altro pregiudiziale: esisteva una certa esitazione nello studiare
il moto di particelle a velocità superiore a quella della luce, visto il
recente riconoscimento del postulato limte della velocità della luce
dovuto ad Einstein. Chiaramente questa obiezione era del tutto infondata su una base rigorosamente scientifica, visto che qui si stava
studiando il moto di una particella in un mezzo, dove la velocità
della luce è inferiore a quella della luce nel vuoto e dunque non si
entrava affatto in contraddizione con il postulato einsteniano. La
teoria sviluppata prediceva la dipendenza dell’angolo di emissione
dalla velocità della particella e dall’indice di rifrazione del mezzo,
la distribuzione spettrale e l’intensità totale dell’energia. Le previsioni teoriche furono confermate sperimentalmente da Cherenkov
che definitivamente validò la teoria. Cherenkov pubblicò i risultati
completi delle sue ricerche nel 1944. Nel 1940 Ginzburg sviluppò la
teoria della radiazione Cherenkov in un mezzo anisotropo e aggiunse
una trattazione quantistica di suddetto effetto. Le sue conclusioni
erano molto simili a quelle di Tamm e Frank.
8
L’importanza di questo effetto può essere riconosciuta se si pensa
che durante i primi 30 anni dalla sua scoperta i fisici di tutto il
mondo hanno scritto più di 500 articoli sui suoi aspetti teorici e le sue
applicazioni. Ad oggi non esistono ancora osservazioni sperimentali
che contraddicano le conclusioni di Tamm e Frank. Inoltre, tutti gli
esperimenti condotti non hanno fatto altro che confermare, a livelli
di maggior precisione, i risultati di Cherenkov. Nel 1943 fu conferito
il premio di Stato USSR a Cherenkov, Vavilov, Tamm e Frank per
la scoperta di questo nuovo tipo di radiazione. Nell’Ottobre del
1958 il Premio Nobel per la fisica fu conferito a Cherenkov, Tamm
e Frank. Vavilov non potè riceverlo giacchè secondo il regolamento
non è possibile conferirlo post mortem.
Fino ad oggi l’effetto è noto come radiazione Cherenkov. Frank,
nondimeno, ha sempre rimarcato la paternità di Vavilov nella scoperta, suggerendo che esso dovesse esser chiamato “radiazione Cherenkov
- Vavilov ” e infatti con questo nome è tuttora nota nei paesi dell’ex
Unione Sovietica.
1.2 Fenomenologia dell’effetto Cherenkov
Per la teoria della relatività nessuna particella può viaggiare a velocità superiore a quella della luce nel vuoto. In un mezzo denso però,
la velocità della luce risulta più bassa di quella di propagazione
nel vuoto, e in un mezzo con indice di rifrazione n, risulterà pari
a c/n. Può dunque avvenire che una particella superi la velocità
di propagazione della luce nel mezzo, pur tuttavia restando al di
sotto di c. Se tale particella è carica elettricamente allora si verifica
l’effetto Cherenkov.
Consideriamo una particella carica che viaggia a velocità v costante
attraverso un mezzo trasparente il cui indice di rifrazione, n, risulti
maggiore di 1. La particella che attraversa il mezzo genera un
campo elettromagnetico che polarizza gli atomi del mezzo in questione. Immaginiamo che la particella carica sia un protone, allora
gli atomi vengono deformati in modo che gli elettroni vengono a
trovarsi più vicini alla particella con carica positiva. Gli elettroni ritornano alla posizione d’equilibrio dopo che la particella (e dunque
il campo di polarizzazione) è passata, emettendo fotoni. Questo
fenomeno avviene solo se il mezzo materico è un dielettrico, giacchè se si tratta di un conduttore, gli elettroni possono ritornare in
9
Figure 1:
sferica.
Polarizzazione in condizioni normali: si evidenzia una simmetria
posizione d’equilibrio anche senza emettere fotoni.
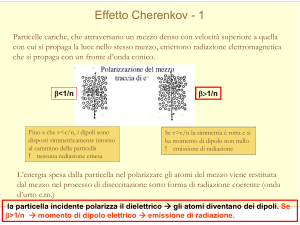
In condizioni normali, cioè per v<c/n, la polarizzazione ha simmetria sferica (vedi Figura 1), i fotoni emessi interferiscono distruttivamente e quindi la radiazione emessa risultante è nulla.
Invece, in condizioni superluminali, cioè per v>c/n, la particella viaggia più velocemente del campo di polarizzazione e quindi
il mezzo è polarizzato soltanto dietro la particella, mentre gli atomi
davanti alla particella non hanno subito polarizzazione (vedi Figura
2). In questo caso i fotoni emessi interferiscono costruttivamente
e dunque viene emessa la radiazione Cherenkov. Vale la pena di
sottolineare che questa radiazione è generata dal mezzo stesso e non
direttamente dalla particella che lo attraversa.
Come nell’aria, quando un oggetto supera il muro del suono, si
forma un cono d’onda (onde meccaniche), allo stesso modo, con le
onde elettromagnetiche, nelle condizioni sopra enunciate, si assiste
alla produzione di un cono d’onda del tutto simile al cono di Mach
per il suono.
Il fronte d’onda Cherenkov può essere costruito utilizzando il
principio di Huygens: nell’intervallo di tempo t l’onda percorre una
distanza tcn e la particella percorre una distanza tβc. Da queste due
10
Polarizzazione in condizioni superluminali: il mezzo è polarizzato solo dietro alla particella.
Figure 2:
distanze, con semplice trigonometria, si può ottenere la direzione di
propagazione dell’onda Cherenkov, come si può vedere osservando
la Figura 3.
Risulta:
cosθ =
tc
n
tβc
=
1
.
βn
(1)
La radiazione viene emessa solo se si verifica la condizione: β > n1 .
Se la velocità della particella è uguale a quella della luce nel mezzo,
non si verifica alcuna radiazione. Invece l’angolo massimo si ha
quando la particella si muove a velocità c. In tal caso la relazione
diviene cosθ= n1 .
Il rilevamento di radiazione Cherenkov è oggi sfruttato ampiamente in astronomia delle sorgenti gamma e per gli esperimenti
condotti sui neutrini, rilevando ad esempio i neutroni prodotti in
acqua, i quali, essendo negativamente carichi, e viaggiano ad una velocità superiore a quella della luce in acqua, danno luogo all’effetto
Cherenkov.
11
Costruzione del fronte d’onda della radiazione emessa a partire
dal cono Cherenkov.
Figure 3:
1.3 Aspetti Microscopici e Macroscopici
Gli elettroni superluminali prodotti dallo scattering Compton dei
raggi γ incidenti con gli atomi di materia attraversata, muovendosi nel mezzo dielettrico con moto rettilineo uniforme irradiano
raggi γ, ossia generano la radiazione Cherenkov. La spiegazione del
fenomeno data da Tamm e Frank parte dalle equazioni di Maxwell
in un mezzo dielettrico, che forniscono una descrizione macroscopica della dinamica del campo elettromagnetico. Come è noto, queste
equazioni rappresentano un metodo nobile ed efficace per tener conto
delle cariche di polarizzazione che si creano nel mezzo per azione
delle cariche “libere”. Infatti, il campo elettromagnetico, risulta dalla
sovrapposizione del campo prodotto dalla particella nel vuoto e dal
campo prodotto dalle cariche di polarizzazione. Siccome una particella in moto rettilineo uniforme nel vuoto non origina alcun campo
di radiazione, a livello microscopico, la radiazione Cherenkov deve
dunque originare dalle cariche di polarizzazione. A livello microscopico, infatti, l’elettrone in moto nel mezzo modifica le molecole
conferendo loro un momento di dipolo elettrico che scompare immediatamente dopo il passaggio dell’elettrone. Le cariche che compongono i momenti di dipolo sono così sottoposte ad un’accelerazione
quasi - istantanea, e divengono dunque sorgenti impulsive di onde
12
elettromagnetiche elementari, che si manifestano a livello macroscopico come radiazione Cherenkov. Tuttavia, non è immediato valutare il campo macroscopico, valutando esplicitamente la sovrapposizione coerente di queste infinte onde elementari “microscopiche”.
Viceversa, le equazioni di Maxwell in un mezzo costituiscono uno
strumento molto efficace per valutare il campo elettromagnetico
prodotto a livello macroscopico dalla particella e dalle cariche di
polarizzazione da essa indotte. Per semplicità è tuttavia usuale parlare di “campo prodotto e energia irradiata dalla particella” piuttosto
che dalle cariche di polarizzazione, come in realtà risulta.
1.4 La teoria di Tamm e Frank
Consideriamo un dielettrico isotropo, infinito e omogeneo, con permeabilità magnetica uguale a quella del vuoto, � = 1, e con costante
dielettrica ε > 1 e reale. Stiamo così trascurando l’assorbimento
del mezzo, ipotesi giustificata per frequenze lontane dalla frequenza
di risonanza. La teoria sviluppata da Tamm e Frank applica le
equazioni dell’elettrodinamica classica al caso di una particella carica che attraversa un mezzo dielettrico, le cui proprietà sono descritte dal solo parametro macroscopico ε. Tale analisi può essere
affrontata in suddetto modo poichè la lunghezza d’onda della radiazione considerata ( λ ∼ 10−5 cm ) è molto maggiore delle distanze interatomiche nel mezzo ( λ ∼ 10−8 cm ). Consideriamo una
particella carica che si muove di moto rettilineo uniforme in un
mezzo dielettrico con queste caratteristiche, le equazioni di Maxwell
si scriveranno:
� ×H
� = 4π�j + 1 ∂ D
�
∇
c
c ∂t
(2)
� ×E
� = −1 ∂ B
�
∇
c ∂t
(3)
� ·B
� =0
∇
(4)
� ·D
� = 4πρ
∇
(5)
13
� = εE.
� Introducendo il potenziale vettore A
� e quello scalare
con D
�
�
φ si ottiene per i campi E ed H:
� =∇
� ×A
�
H
(6)
� = −∇φ
� −1 ∂A
�
E
c ∂t
(7)
I potenziali soddisfano inoltre la gauge di Lorentz:
� ·A
�+ε ∂φ=0
∇
c ∂t
dando luogo alle seguenti equazioni disaccoppiate:
(8)
�−
�A
ε2 ∂ 2 �
4π
A = − �j
2
2
c ∂t
c
(9)
�φ −
ε2 ∂ 2
4π
φ=− ρ
2
2
c ∂t
c
(10)
In un mezzo dispersivo la costante dielettrica dipende dalla frequenza ω del campo elettromagnetico e dunque anche la relazione
� ed E
� dipenderà dalla frequenza:
fra D
�
�
�
D(ω)
= ε(ω)E(ω)
= n2 (ω)E(ω)
con n(ω) indice di rifrazione del mezzo alla frequenza ω.
Tutte le grandezze fisiche fino ad ora introdotte possono essere
scritte in termini della frequenza semplicemente facendo la trasformata di Fourier:
´
´
´
iωt
iωt
iωt
� = +∞ E(ω)e
�
� = +∞ D(ω)e
�
� = +∞ A(ω)e
�
E
dω;
D
dω;
A
dω
−∞
−∞
−∞
etc...
e quindi, ad esempio, l’equazione dell’elettromagnetismo disac� esplicita le seguenti dipendenze funcoppiata per il potenziale A
zionali:
2
2
�
�
�A(ω)
− ε2 ∂ 2 A(ω)
= − 4π�j(ω).
c ∂t
c
In seguito supporremo che la particella si muove lungo l’asse z ,
quindi con traiettoria �y (t) = (0, 0, vt). In questo caso conviene introdurre le coordinate cilindriche vista la simmetria assiale del nostro
problema, �x(t) ←→ (z, r, φ), dove r e φ sono coordinate polari bidimensionali, nel piano ortogonale alla traiettoria della particella. In
particolare r indica la distanza di �x(t) dall’asse z . La densità di
carica della particella in moto si scriverà:
14
jz (ω) = 2πe2 ρ e−
iωz
v
δ(ρ); jx (ω) =jy (ω) = 0.
In coordinate cilindriche, Aρ (ω) =Aφ (ω) = 0, si ottiene dunque
la seguente equazione:
∂ 2 Az
1 ∂ ∂Az (ω)
ω2 ε
2e − iωz
+
(ρ
) + 2 Az (ω) = −
e v δ(ρ)
2
∂z
ρ ∂ρ
∂ρ
c
πρc
(11)
Se si assume che la soluzione abbia una forma del tipo:
Az (ω) =
e − iωz
e v a(ρ)
2c
(12)
allora a(ρ) soddisfa la seguente equazione:
∂ 2 a(ρ, ω) 1 ∂a(ρ, ω)
4
+
) + s2 a(ρ, ω) = − δ(ρ)
2
∂ρ
ρ ∂ρ
πρ
(13)
dove
s2 =
ω2 2 2
v
(β n - 1 ) = - σ�2 ; β =
2
v
c
(14)
Si può provare che la funzione a(ρ, ω) è una funzione cilindrica
che soddisfa un caso speciale dell’equazione normale di Bessel:
��
�
u + z1 u + u = 0.
In questo caso la variabile è z = ρs. Si ha allora l’equazione per
a(ρ) valida per ogni ρ tranne che per ρ = 0:
∂ 2 a(z, ω) 1 ∂a(z, ω)
+
+ a(z, ω)=0
∂z 2
z ∂z
(15)
La soluzione generale è del tipo:
(1)
(2)
a(z, ω) = C1 H0 + C2 H0
(1)
dove H0
specie:
(2)
e H0
(16)
sono le funzioni di Hankel di prima e seconda
(1)
H0
(2)
=
H0 =
�
�
2 i(sρ− π )
4
e
πρs
2 −i(sρ− π )
4
e
πρs
15
(17)
(18)
e C1 e C2 sono costanti di normalizzazione determinate fissando
le condizioni al contorno del problema.
La scelta delle soluzioni dell’equazione necessita una distinzione
di due casi. Il primo, quando si hanno piccole velocità, cioè quando
βn < 1 e dunque s è un numero immaginario. Dall’espressione per
(2)
le funzioni di Hankel si vede che per ρ �−→ ∞ la funzione H0 �−→
∞. Quindi si ha C2 = 0 e dal calcolo delle condizioni al contorno
possiamo determinare C1 = i. Dunque la soluzione risulta:
a(z, ω) =
(1)
iH0 (sρ)
=i
�
2 i(sρ− π )
4
e
πρs
(19)
per ρ �−→ ∞ e s2 < 0, a(sρ) �−→ 0, cioè a grandi distanze il campo
decresce esponenzialmente o alternativamente a piccole velocità la
particella non irraggia.
Un risultato completamente differente si ottiene per βn > 1. In
(1)
questo caso s è reale, e per ρ �−→ ∞ entrambe le funzioni H0 e
(2)
H0 rappresentano un’onda cilindrica. In guisa da ottenere delle
soluzioni che soddisfano il principio di radiazione, cioè vogliamo ottenere delle onde uscenti (solo in questo caso otteniamo onde la cui
fase va all’infinito), ritorniamo alla rappresentazione di Az secondo
la trasformata di Fourier:
´ +∞
Az = −∞ Az (ω)eiωt dω
iωz
con Az (ω) = 2ce e− v a(ρ, ω). Dalla forma asintotica delle funzioni
di Hankel ne segue che per soddisfare il principio di radiazione (ωt
e sρ di segno diverso), bisogna scegliere le soluzioni:
(1)
(20)
(1)
(21)
a(ρ, ω) = iH0 (sρ); ω < 0
a(ρ, ω) = iH0 (sρ); ω < 0
ottenendo così la soluzione:
Az (ω) =
ˆ+∞
−∞
e − iωz iωt
(2)
e v e (−iH0 (sρ))dω = −
2c
ˆ+∞
−∞
16
z
π
ei
�
eiω(t− v )−isρ+i 4 dω
c 2πsρ
(22)
con ω > 0.
c
n
Ricordando la definizione di s2 e ponendo (βn)−1 = cosθ e u =
= vcosθ si ottiene:
Az = −
+∞
ˆ
−∞
Az = −
ρsenθ+zcosθ
ei
)+i π4
u
√
eiω(t−
dω
c 2πsρ
(23)
ρsenθ+zcosθ
)+i π4
√ei eiω(t−
u
dω
−∞ c 2πsρ
´ +∞
o equivalentemente:
Az = −
�
2
π
con
η = ω(t −
+∞
ˆ
−∞
ei
c
�
1
cosηdω
sρ
ρsenθ+zcosθ
)
u
(24)
+ π4 .
L’equazione 24 è nota come Prima formula della teoria di
Tamm e Frank.
In questo modo Az risulta la somma di onde coniche di frequenza
ω che si propagano ad un angolo θ lungo l’asse z, coincidente con
la direzione di moto della particella. Ciò può essere evidenziato
facilmente. Infatti, l’equazione di un’onda che si propaga dall’origine
nella direzione R con velocità v ha la forma:
R
A ∼ eiω(t- v )
In coordinate polari, per un’onda che si propaga lungo R ad un
angolo θ rispetto a z, si ha che R = ρsenθ+zcosθ (vedi Figura 4 )
e quindi l’equazione di un’onda conica, usando l’espressione appena
data diviene:
A ∼ eiω(t-
ρsenθ+zcosθ
)
v
ma questa è proprio l’espressione che compare nella 23.
Quindi per βn > 1 la radiazione si propaga solo nella direzione θ
rispetto alla direzione di moto. Quest’angolo è legato alla velocità
β = vc dalla semplice relazione:
cosθ (ω)=
17
1
n(ω)β
(25)
Figure 4:
Un’ onda conica in coordinate polari.
dove n(ω) è l’indice di rifrazione assoluto del mezzo per una data
frequenza ω. L’equazione 25 esprime una delle proprietà basilari
della radiazione Cherenkov: il suo carattere fortemente collimato
in avanti. Le direzioni di emissione dunque giacciono su
un cono in avanti, coassiale con la traiettoria della
particella e di apertura θ, che viene a ragione detto
cono Cherenkov.
Per trovare l’energia che si propaga all’infinito, bisogna calcolare
il flusso del vettore di Poynting attraverso una superficie cilindrica
unitaria:
ˆ+∞
dW = 2πρdl
Sρ dt
(26)
−∞
dove Sρ è la componente radiale del vettore di Poynting, vettore
S. Per determinare il vettore di Poynting è necessario conoscere le
varie componenti del campo elettrico e magnetico, i cui orientamenti
rispetto alla direzione di moto sono mostrati in Figura 5.
E’ possibile dimostrare con un po’ di conti [1] che la Seconda
Formula della teoria di Tamm e Frank è la seguente:
18
� , H
� eS
� per il cono radiativo
Mutua direzione dei vettori E
Cherenkov.
Figure 5:
dW
e2
= 2
dl
c
ˆ �
nβ>1
1
1− 2 2
βn
�
ωdω
(27)
Essa determina l’energia irradiata per unità di cammino libero
medio. Fornisce sia il flusso di energia totale di una singola particella
che la distribuzione spettrale della radiazione Cherenkov.
1.5 Effetto Cherenkov nel riferimento proprio
L’approccio di Tamm e Frank fornisce una trattazione completa
dell’effetto Cherenkov, tuttavia la trattazione è svolta nel sistema
di riferimento del laboratorio. E’ possibile ricavare le espressioni
dei potenziali in modo più semplice e molto più diretto partendo
dal riferimento proprio, che chiameremo S, in moto con velocità
v (in verso opposto rispetto all’asse x, direzione di moto) rispetto
al sistema del laboratorio. Qui la particella è in quiete per cui le
19
equazioni di Maxwell assumono la seguente forma:
� ·D
� = 4πρ
∇
(28)
� ·B
� =0
∇
(29)
� ×E
� = −1 ∂ B
�
∇
c ∂t
(30)
� ×H
� =1∂D
�
∇
(31)
c ∂t
Queste equazioni rappresentano un campo eletrrostatico, per cui
il quadripotenziale è:
�
�
ie
�
A� = 0,
(32)
Rε
dove ε è la costante dielettrica del mezzo considerato e R è la
distanza, nel riferimento proprio, tra la particella ed il punto in cui
agisce il potenziale. Il calcolo di R si ottiene utilizzando ancora una
volta le trasformazioni di Lorentz, �
partendo dal sistema di riferi�
mento
del
laboratorio,
in
cui
R
=
x� 2 + y � 2 + z � 2 e dunque si ha
�
�
2
R = x� 2 + y � 2 + γ� 2 (ct� + βx ) .
�
Per ritornare al sistema del laboratorio, che chiameremo S è
necessario applicare la trasformata di Lorentz al quadripotenziale
A� :
�
Ax
0
1
0 0
0
A�y 0
1 0
0 0
� =
Az γ
0 0 −iγβ 0
�
ie
−iγβ 0 0
γ
V
Rε
otteniamo così:
�
A� =
�
eγβ ieγ
0, 0,
,
εR Rε
20
�
(33)
Il problema ha simmetria cilindrica, come già chiarito nei paragrafi precedenti, per questo è possibile passare in coordinate cilindriche utilizzando la trasformazione:
x
ρcosφ
y → ρsenφ
z
z
La trasformata di Fourier nel dominio della frequenza della componente z del potenziale (l’unica diversa da zero in quanto Az =
Aρ = 0 per la simmetria) è :
A(ω)=
ˆ
Az (t)e
−iωt
dt =
�
2
π BesselK
�
�
0,
Abs[ω]
�
c2 β2 γ2
c 2 β 2 γ2
a2
�
(34)
Questo risultato è perfettamente in accordo con quello determinato a partire dalla teoria di Tamm e Frank. Il calcolo dell’energia
irradiata per effetto Cherenkov procede esattamente come descritto
nel paragrafo precedente.
Partire dal riferimento proprio è stato molto vantaggioso perché
ha consentito di calcolare i potenziali semplicemente partendo da
una trasformazione di Lorentz. Tuttavia questo metodo di procedere
è valido solo se siamo in un mezzo non dispersivo (cioè l’indice di
rifrazione risulta indipendente dalla frequenza ω). In questo caso,
infatti, la trasformata di Lorentz, mescolando le coordinate spaziali
con quelle temporali, non consentirebbe di giungere alle corrette
espressioni per i potenziali.
1.6 Relazioni costitutive
1.6.1 Introduzione
Analizzando le equazioni di Maxwell in un mezzo materico, cioè le
equazioni 1, 3, 4 e 5, è possibile notare che esse contengono una densità di corrente elettrica, che è stata indicata come �j. Una denistà
di corrente è sempre costituita da cariche in movimento, ma il moto,
nel caso in esame, può essere dovuto a due diverse cause:
1.
Forze esterne al campo elettromegnetico che stiamo considerando;
21
2.
La forza di Lorentz dovuta al campo descritto dalle equazioni
di Maxwell.
Di conseguenza è possibile dividere la densità di corrente in due
parti:
�j = �j 0 + �jind
dove �j0 viene detta densità di corrente impressa ed è attribuibile
alla prima causa, laddove �jind è detta densità di corrente indotta o
sostenuta dal campo ed è attribuibile alla seconda causa.
Entrambe le correnti risultano essere sorgenti del campo elettromagnetico. Tuttavia, mentre la corrente indotta risulta un’incognita
del problema, quella impressa è da considerarsi un dato (�j0 è un termine noto nelle equazioni di Maxwell).
Ricordando che le quazioni alle divergenze contengono informazioni
già presenti nelle equazioni ai rotori, le equazioni di Maxwell in� B,
� E,
�
dipendenti sono solo 2, per un totale di 5 incognite ( D,
� �j). Sono dunque necessarie 3 equazioni vettoriali per risolvere
H,
il problema dell’elettromagnetismo nei mezzi materici. Queste relazioni sono comunemente dette Relazioni Strutturali.
Lo studio del campo elettromagnetico in un mezzo non può prescindere da quelle che sono le proprietà del mezzo che stiamo considerando. Fisicamente i costituenti elementari reagiscono al campo
elettromagnetico, dando vita a fenomeni di polarizzazione e magnetizzazione, dipendenti dal campo stesso, che quindi entrano nella
definizione degli altri vettori di campo.
Ovviamente ogni mezzo ha il suo proprio insieme di equazioni
costitutive, ma è possibile classificarle in base alle proprietà che
soddisfano e studiare quindi il campo in un mezzo che gode di certe
proprietà (lasciandone i parametri non specificati).
Nel caso del vuoto queste relazioni sono:
� = ε0 E
�
D
� =� H
�
B
0
�j = �0
In un mezzo materico qualunque, le relazioni costitutive saranno
diverse in quanto i costituenti microscopici de mezzo si polarizzano.
22
E’ conveniente introdurre il vettore polarizzazione P� e magnetiz� , definite da:
zazione M
� = ε0 E
� + P�
D
(35)
� =�H
� +M
�
B
0
(36)
1.6.2 Proprietà Strutturali
E’ possibile dividere le proprietà strutturali di un qualsiasi mezzo
materiale in proprietà di Simmetria e proprietà Strutturali. Tra
queste ultime hanno notevole importanza l’indipendenza da una
delle due cause e la linearità.
� dipende solo da H,
�
Per la maggiorparte dei materiali si ha che B
�
�
�
mentre D, j solo da E. E’ evidente che si stanno trascurando sia
� oppure i mezzi chirali, in
l’effetto Hall, dove �j dipende anche da E,
�
�
�
�
cui B e D dipendono sia da E che da H.
� (oppure P� ) ed E
�
Consideriamo ad esempio la relazione fra D
(che è quella del comportamento più vario), ma anche per le altre
valgono discorsi analoghi.
Si dice che il mezzo è Lineare, se ad una qualunque
combinazione lineare delle cause corrisponde una combinazione lineare degli effetti con gli stessi coefficienti.
Un mezzo è lineare se e solo se tutte le relazioni sono lineari
(ovviamente in un mezzo non lineare due possono esserlo e una no
e così via).
Se si assume anche che il mezzo sia stabile (ossia l’effetto tende
a zero se la causa tende a zero) è possibile scrivere la relazione tra
� in forma integrale generalizzato:
P� ed E
P�(�r, t) =
ˆ
R3
ˆ+∞
�
� r�� , t� )dt� dV �
G(�r, r�� ; t, t )E(
(37)
−∞
dove G è una matrice 3x3 di funzioni1 che si annullano in modo
sufficientemente rapido all’infinito. Ovviamente tutti i materiali
1 Gli elementi di G possono più in generale essere distribuzioni. Ad esempio la relazione
� ed E
� nel vuoto, può essere espressa nella forma precedente usando come G una matrice
fra D
diagonale i cui elementi sono delle δ di Dirac.
23
sono, a rigore, non lineari in quanto, per campi sufficientemente
intensi si ha la scarica disruptiva. Allo stesso tempo, per opportuni
� ogni mezzo soddisfa ad una relazione
intervalli di variazione di E,
costitutiva lineare(fa eccezione il solo vuoto, che nell’ambito della
fisica classica, è sempre lineare).
In altri termini studiamo come mezzi lineari quei mezzi che non
hanno soglia (per campi di interesse) e che non vengono sollecitati
con campi così intensi da provocare effetti di saturazione o di rotture
del dielettrico. Esempi di mezzi non lineari sono:
P�(�r, t) = χ
ˆ
R3
�
�
�
� � �� � �2
� =
�E(r , t )� dV− e_D
�
ε0 E
� �2
���
�E �
1 + E2
(38)
M
dove E M e χ sono delle costanti. Nel primo caso, in particolare,
i coefficienti della combinazione lineare sono diversi. Notiamo però,
� � EM , il mezzo può essere considerato
nel secondo caso, che se E
lineare.
Prima di passare alle proprietà, che discuteremo solo nel caso lin�
eare, conviene analizzare più in dettaglio il significato di G(�r, r�� ; t, t ).
Per un ingresso impulsivo si ha:
e quindi si ha:
� r, t) = E�0 δ(�r − �r0 )δ(t − t0 )
E(�
(39)
P�(�r, t) = G(�r, r�0 ; t, t0 ) · E�0
(40)
con E�0 vettore costante.
�
Quindi G(�r, r�� ; t, t ) è la risposta impulsiva (generalizzata per
tener conto che ingresso e uscita sono vettori) del mezzo in esame.
La richiesta di causalità (l’effetto non può precedere la causa) e
la considerazione che i rapporti causa - effetto devono andare alla
velocità della luce fanno sì che:
�
�
��r − r�0 �
.
(41)
G(�r, r�0 ; t, t0 ) = 0−se−t < t0 +
c
La relazione precedente deriva dal fatto che G(�r, r�0 ; t, t0 ) è l’effetto
in (�r, t) di una causa posta in (�
r0 , t0 ) .
24
Un’ulteriore importante proprietà strutturale è la non dispersività. Un mezzo si dice non dispersivo nello spazio (locale) se l’effetto dipende solo dalla causa nel medes� non vi è l’integrale
imo punto. In tal caso nella relazione fra P� ed E
�
�
in dV− (o, equivalentemente, G(�r, r�� ; t, t ) ha come fattore, δ(�r − r�� ) ).
Analoga definizione vale per la non dispersività nel tempo (mezzo istantaneo). Si noti tuttavia che se un mezzo è dispersivo nello spazio
deve necessariamente esserlo anche nel tempo (chiaramente, negando la precedente proposizione logica, la non dispersività spaziale
implica la non dispersività temporale). Infatti se l’effetto in r�1
dipendesse dalla causa in r�0 (�= r�1 ), dovrebbe dipendere dal valore
di questa causa in istanti precedenti, in quanto la relazione causa
- effetto non viaggia istantaneamente. Quindi i mezzi fiscamente
realizzabili possono essere solo:
•
istantanei;
•
non dispersivi nello spazio;
•
dispersivi.
Poichè l’interazione campo - materiale che ne determina le proprietà
dielettriche avviene come reazione del campo sul moto dei costituenti
elementari, sarà sempre presente un effetto d’inerzia e quindi una
dispersività nel tempo. La sua importanza dipende dalla velocità di
variazione del campo: per frequenze molto basse la risposta si può
assumere, in genere, istantanea, (almeno per costituenti in qualche
modo legati) e a frequenze elevate si può assumere nulla (assenza di
effetti dielettrici). Tra questi due estremi il mezzo va invece considerato dispersivo.
La dispersività spaziale tende invece ad annullarsi per distanze
� r0 ) ha effetto
grandi rispetto a quelle
atomiche.
In altri termini E(�
�
�
su P� (�r) se e solo se ��r − r�0 � < a con a confrontabile alla dimensione
� è, alle frequenze d’interesse (siamo nel dominio
atomica. Poichè E
delle onde radio), sostanzialmente costante su tale scala, allora la
dispersività spaziale comporta solo una piccola variazione alle relazioni dispersive e può essere in genere trascurata.
Diverso è il discorso in presenza di moti di cariche libere dovute
a cause diverse dal campo elettrico (metalli, soluzioni elettrolitiche,
plasmi), oppure a frequenze molto elevate (infrarosso, visibile).
25
1.6.3 Proprietà di Simmetria
Consideriamo ora le proprietà di simmetria, ovvero di invarianza
rispetto alle trasformazioni spaziali e temporali. Un mezzo si dice:
•
Stazionario (Omogeneo nel Tempo) se ad una traslazione
temporale della causa corrisponde una traslazione temporale
dell’effetto;
•
Omogeneo nello Spazio se ad una traslazione spaziale della
causa corrisponde una traslazione spaziale dell’effetto;
•
Isotropo se ad una rotazione della causa corrisponde una
rotazione dell’effetto.
L’esistenza di proprietà di simmetria ha ovviamente dei riflessi sulle
relazioni costitutive. Ci occuperemo nel dettaglio della sola omoegenità.
OMOGENEITA’
Fisicamente ogni sistema isolato all’equilibrio è stazionario. Mezzi
non stazionari sono quindi dovuti a cause esterne che includiamo per
comodità nelle relazioni costitutive. Un esempio tipico è la dipendenza dalla temperatura delle relazioni costitutive: se facciamo variare T dall’esterno con legge nota il mezzo diviene non stazionario.
Viceversa, ogni materiale è, su scala atomica, non omogeneo a causa
della natura atomica delle fluttuazioni. Se però la scala di variazione
del campo è grande rispetto alla scala atomica possiamo considerare il materiale omogeneo (a meno che non sia intenzionalmente non
omogeneo, come materiali plastici riempiti di sferette di vetro).
�
Se un mezzo è stazionario, allora G(�r, r�� ; t, t ) non dipende sepa�
�
ratamente da t−e−t , ma solo dalla differenza t−t . Per dimostrarlo
si consideri una qualunque causa E�0 (t) e il corrispondente effetto
P�0 (�r). Si ha allora2 ∀�r, τ:
+∞
ˆ
P�0 (t) =
G(t, t� ) · E�0 (t� )dt�
(42)
−∞
P�0 (t + τ) =
+∞
ˆ
G(t + τ, t� ) · E�0 (t� )dt�
−∞
2 In
questa dimostrazione non indichiamo per semplicità la dipendenza spaziale
26
(43)
Trasliamo ora la causa di −τ, ovvero consideriamo come
´ +∞causa �
�
�
E0 (t−τ). La polarizzazione corrispondente vale P0 (t−τ) = −∞ G(t, t )·
E�0 (t� − τ)dt� e, se il mezzo è omogeneo, tale polarizzazione deve essere uguale a P�0 (t) traslato di −τ, ossia P�0 (t − τ). Dall’uguaglianza
delle due espressioni di P�0 (t − τ) segue che:
ˆ+∞
ˆ+∞
�
�
�
G(t − τ, t ) · E�0 (t )dt =
G(t, t� ) · E�0 (t� − τ)dt� −−∀τ
−∞
−∞
��
�
Ponendo nel secondo integrale t = t − τ, e portando tutto al
primo membro:
ˆ+∞
ˆ+∞
��
��
��
�
�
�
G(t − τ, t ) · E�0 (t )dt −
G(t, t + τ) · E�0 (t )dt = 0−−∀τ
−∞
−∞
ˆ+∞�
G(t − τ, t ) − G(t, t + τ) · E�0 (t� )dt� = 0−−∀τ
ˆ+∞�
�
�
G(t − τ, t� ) − G(t, t + τ) · E�0 (t� )dt� = 0−−∀τ
−∞
�
�
�
Il prodotto scalare coinvolto è un prodotto matrice per vettore.
�
Possiamo per semplicità scegliere E�0 (t ) lungo un qualunque asse,
ad esempio l’asse x e la relazione precedente fornisce, se proiettata
sugli assi, tre relazioni scalari:
ˆ+∞�
−∞
−∞
�
�
Gix (t − τ, t� ) − Gix (t, t + τ) · E�0 (t� )dt� = 0−−∀τ e ∀ i = x,y,z.
�
Questa relazione vale ∀E0 (t ) e ∀t. Possiamo allora scegliere
�
un E0 (t ) pari alla quantità in parentesi quadre e si ottiene che
l’integrale di una grandezza non negativa è nullo:
ˆ+∞�
−∞
�
Gix (t − τ, t� ) − Gix (t, t + τ)
27
�2
dt� = 0−−∀τ,t.
Tuttavia questo integrale può essere nullo se e solo se l’integrando
è nullo e dunque, ripetendo il tutto per ciascuna componente, otteniamo:
�
G(t − τ, t� ) = G(t, t + τ)−−∀τ,t,t’.
Scelto t� = 0 segue che
�
G(t − τ, 0) = G(t, t )−−∀τ,t.
(44)
ovvero la tesi.
� r, t)
Se poi il mezzo è anche non dispersivo si ha P� (�r, t) = G(�r)· E(�
ovvero G non dipende dal tempo. Analogamente, considerando un
mezzo che riempie tutto lo spazio, si trova che in un mezzo omogeneo
nello spazio, G dipende solo da �r − r�� .
DOMINIO DELLA FREQUENZA
Si consideri un mezzo omogeneo e lineare nel tempo. Per esso si ha,
in luce di quanto su detto:
´ ´ +∞
�
� r�� , t� )dt� dV �
P�(�r, t) = R3 −∞ G(�r, r�� ; t − t )E(
ed è possibile passare nel dominio della frequenza.
�
�
� = Re E�0 ej(ωt+Φ) , con E�0 ≡
Infatti se il campo elettrico è E
E�0 (�r) e Φ ≡ Φ(�r), allora:
�´ ´
�
�
�
�
�
+∞
P�(�r, t) = Re R3 −∞ G(�r, r�� ; t − t )E�0 ej(ωt +Φ) dt dV =
�´ ´
�
�
�
�
�
+∞
P�(�r, t) = Re R3 −∞ dt G(�r, r�� ; t − t )ejωt E�0 ejωΦ dV
operando il cambiamento di variabile t� = t − τ otteniamo:
� ´ ´
�
�
+∞
P�(�r, t) = Re − R3 −∞ dτG(�r, r�� ; τ)e−jωτ E�0 ejωΦ dV
ma l’integrale in dτ non è altro che la trasformata di Fourier di
G. Poniamo:
´ +∞
�
� r�� , t� )dt� dV �
T = ε0 I + −∞ G(�r, r�� ; t − t )E(
dove I è la matrice identità.
Considerando le grandezze nel DF si ha:
28
� r, ω) = ε0 E(�
� r, ω) + P�(�r, ω) = ´ 3 T (�r, r�� )E(
� r�� )dV �
D(�
R
� = E�0 ejΦ . Ovviamente T dipende dalla frequenza e va
essendo E
quindi utilizzato il valore delle frequenza delle sorgenti.
Se il mezzo è anche non dispersivo nello spazio, allora nella relazione precedente scompare l’integrale. La trasformata di G viene
indicata con ε - ε0 I e risulta:
� r, ω) = ε(�r, ω) · E(�
� r, ω)
D(�
(45)
dove ε(�r, ω) generalizza il concetto di costante dielettrica. Essendo una trasformata di Fourier essa dipende da ω: tuttavia, per
mezzi non dispersivi nel tempo, ne risulta indipendente. In assenza
di dispersione segue facilmente che se il mezzo è omogeneo, allora
ε non dipende da �r. Si può inoltre dimostrare [2] che, in assenza
di campi magnetici esterni, la matrice ε è simmetrica e ovviamente
diventa uno scalare in caso di isotropia.
� e tra B
� e H,
� esse
Per quanto riguarda le relazioni tra J� ed E
sono, nei casi più semplici:
�
� =�·H
�
J� = σ� · E−−e−−
B
(46)
dove σ� (che può anche essere nulla) e � dipendono al più da �r.
Per frequenze elevate, però, suddette relazioni divengono dispersive,
ovvero σ� dipende anche da ω. Eccezioni notevoli sono le ferriti mag� e H
� è fortemente non lineare
netizzate: in esse la relazione fra B
ma, se applichiamo un campo magnetico statico che saturi la ferrite
� l’induzione che
e a questo sovrapponiamo un campo variabile H,
� (con ottima approssiquest’ultimo crea dipende linearmente da H
mazione). Il materiale è però anisotropo e dispersivo nel tempo.
1.7 Radiazione Cherenkov dal punto di vista
quantomeccanico
Consideriamo una particella con massa a riposo m0 con velocità v
che viaggia attraverso un mezzo trasparente il cui indice di rifrazione
è n. La particella può emettere un fotone di frequenza ν ad un angolo
θ rispetto alla sua direzione di moto. La particella acquisterà un
ulteriore momento dovuto al rinculo e cambierà la sua direzione.
Sia u la velocità della particella dopo l’emissione del fotone e Φ
29
l’angolo del cambiamento di direzione. Allora per la conservazione
del quadrimpulso si ha:
n
m0 v
h
m0 u
asse−x:− �
= cosθ+ �
cosΦ
2
2
λ
1 − vc2
1 − uc2
asse−y : −0 =
h
m0 u
sinθ+ �
sinΦ
2
λ
1− u
c2
m0 v
h
m0 c2
conservazione−E : − �
= +�
2
2
λ
1 − vc2
1 − uc2
Risolvendo per cosθ si ottiene:
�
c
cos θ = nv
+h 1−
cos θ =
h
√
v 2 n2 −1
c2 2m0 vn2 λ
1
n2 − 1
+Λ
βn
2n2 λ
(47)
1−β2
dove Λ = m0 v è la lunghezza d’onda di De Broglie della particella prima dell’emissione del fotone. Si vede che l’espressione differisce da quella classica (vedi la 1)per un termine additivo. Tuttavia, la grandezza di questo termine è molto piccolo, ed anche per
un elettrone è solo dell’ordine di 10−6 , impossibile da rivelare sperimentalmente.
1.8 Soglia della radiazione Cherenkov
La soglia per la radiazione Cherenkov in un mezzo isotropo dipende
dal rapporto tra la velocità della particella v e la velocità della luce
nel mezzo nc . La radiazione avviene solo quando v > nc . Dal momento che cos θ ≤ 1 si ha sempre nβ ≥1 o equivalentemente v ≥ nc .
La soglia della reazione è dunque:
nβ = 1
(48)
Se tale relazione è soddisfatta non c’è radiazione. E’ usuale in
letteratura indicare la velocità di Threshold (soglia) come segue:
30
c
.
(49)
nmax
La soglia per la radiazione Cherenkov è caratterizzata non solo
dal fatto che l’angolo va a zero, am anche da un’intensità nulla.
Questa relazione è molto utilizzata in esperimenti nei quali l’intensità
della radiazione è misurata in funzione della velocità della particella.
Nella tabella che sugue è possibile vedere l’Energia di Soglia per alcune particelle elementari considerando un indice di rifrazione pari
a naria :
vth =
Particella
Elettrone
Muone
Mesone
Protone
Energia a riposo (MeV)
0.511
106
140
938
E th (MeV) naria = 1.00029
20.7
43
5670
38000
1.9 Intensità della radiazione Cherenkov e
distribuzione spettrale
Considerando l’equazione 27 possiamo constatare che l’energia emessa
per unità di cammino e unità di frequenza è:
�
�
dW
e2
1
= 2 1 − 2 2 ωdω
(50)
dldω
c
βn
Integrando quest’equazione si ottiene l’energia in funzione di ω
oppure della frequenza ν:
�
�
dW
e2
1
= 2 1 − 2 2 (ω22 - ω21 )
(51)
dl
2c
βn
�
�
dW
e2
1
= 2 1 − 2 2 (ν22 - ν21 )
(52)
dl
2c
βn
Inoltre è possibile fornire l’espressione dell’energia emessa nell’intervallo
di lunghezza d’onda (λ1 , λ2 ):
dW
= 4π2 e2
dl
ˆλ2 �
λ1
1
1− 2 2
βn
31
�
1
dλ
λ3
(53)
L’Intensità della radiazione Cherenkov risulta inversamente proporzionale al cubo della lunghezza d’onda, cioè principalmente concentrata nelle regioni dello spettro elettromagnetico con piccole lunghezze
d’onda. In particolare, a piccole λ lo spettro è limitato dalla regione
dei raggi X (λ ∼ [1−10]Å), dove l’indice di rifrazione diventa minore
di uno e non sono più soddisfatte le condizioni per la radiazione. In
molte applicazioni bisogna conoscere il numero di fotoni emessi da
una particella. Dunque, tenendo presente che W = N hν, dividiamo
l’espressione dell’energia in funzione di ω:
dN
4π2 e2
=
dl
hc2
ˆν2 �
ν1
1
1− 2 2
βn
�
dν
(54)
1
dλ
λ2
(55)
oppure in termini di lunghezza d’onda:
dN
4π2 e2
=
dl
hc2
ˆλ2 �
λ1
1
1− 2 2
βn
d2 N
�
Ne segue che essendo dldλ ∼ λ12 , la maggior parte dei fotoni, e
quindi dell’energia è concentrata nella parte blue dello spettro.
32
Capitolo 2
Rivelatori Cherenkov
2.1 Caratteristiche generali
Una singola particella emette, per effetto Cherenkov, una quantità
di luce molto minore di quella che si genera nei materiali attraverso
il processo di scintillazione. In genere per gli scintillatori si ha
un’efficienza di conversione di 1 fotone per ogni 100 eV di energia persa. Ad esempio, un protone con β = 0.8 che attraversa 1
g/cm2 di uno scintillatore di materiale plastico (�E ∼ 2.5 MeV)
emette circa 2 · 104 fotoni, mentre lo stesso protone nell’attraversare
1 cm di un rivelatore Cherenkov emette solo 150 - 200 fotoni nella
regione del visibile, quindi un fattore 102 in meno. Se il trasporto di
un fotocatodo di un fotomoltiplicatore è dell’1% nello scintillatore
saranno prodotti 100 fotoelettroni, mentre dal rivelatore Cherenkov
si avranno solo 1 - 2 fotoelettroni che possono addirittura essere confusi con fondo dello strumento. Per assicurarsi che le fluttuazioni
nel numero di fotoelettroni emessi dal fotomoltiplicatore non falsino
l’efficienza del rivelatore, bisogna che quest’ultimo sia progettato per
produrre almeno 20 fotoelettroni per particella.
Il metodo migliore di raccolta è quello di utilizzare all’interno di
un rivelatore Cherenkov riflessioni interne totali (TIR), che assicurano la raccolta di tutta la radiazione senza perdite. Per una particella con β = 1 che viaggia in un rivelatore, la condizione di riflessione
interna è automaticamente soddisfatta. Per particelle con β < 1 la
condizione di riflessione è soddisfatta solo se l’angolo Cherenkov è
minore di:
� �
� �
1
1
∗
arccos
≤ θ = arcsin
(56)
nβ
n
Questa condizione è soddisfatta per un rivelatore contenente aria.
E’ conveniente utilizzare radiatori che abbiano un grande indice di
1
rifrazione ( dato che E ∼ (βn)
2 ), una densità ed un numero atomico
piccoli, in modo da ridurre al minimo le perdite d’energia per ionizzazione e scattering multipli. L’indice di rifrazione del radiatore,
33
del fotomoltiplicatore devono essere quanto più simili possibile.
2.2 Contatori ad effetto Cherenkov
I contatori Cherenkov sfruttano un gas radiatore e sono particolarmente usati per la rivelazione di particelle con β > 0.90. La luce
emessa per effetto Cherenkov (solitamente in una banda che va dal
visibile all’ultravioletto) dipenderà principalmente dalla presenza di
bande d’assorbimento da parte del materiale. L’indice di rifrazione
del gas è legato alla sua densità ρ attraverso la legge di Lorentz:
n2 − 1 M
=R
n2 + 2 ρ
(57)
dove M è il peso molecolare ed R il coefficiente di rifrazione
molecolare. Dato che per i gas n � 1, possiamo riscrivere l’equazione
come:
3R
ρ
2M
dalla legge dei gas ideali si ha che:
(58)
n−1�
�
P = ρR T/M
�
dove P è la pressione, T la temperatura assoluta e R la costante
dei gas. Sostituendo nell’equazione 57, si ottiene:
n − 1 = (n0 − 1)P/P0
(59)
η = η0 P/P0 .
(60)
dove il pedice 0 sta ad indicare che la grandezza è misurata alla
pressione atmosferica. Usando la notazione η = n − 1, l’equazione
59 diventa:
La soglia di un contatore può essere modificata variando la pressione. Infatti, se si considera un fascio di particelle tutte uguali,
nota la relazione (ricordando che mβγ è l’impulso della particella
relativistica):
βs γs = √
1
n2
1
��
2η
−1
34
(61)
si ricava che:
βs γs = �
1
2η0 PP0
(62)
il pedice s sta ad indicare la soglia al di sotto della quale non
avviene effetto Cherenkov. Si vede che incrementando la pressione,
la soglia sull’impulso decresce come √1P . In questo modo è possibile
creare un discriminatore di velocità (per fasci di particelle con uguale
impulso).
2.3 Contatore a soglia
La condicio sine qua non affinché si verifichi l’effetto Cherenkov
riguarda la velocità della particella che deve superare il valore minimo, ossia di soglia, βt = n1 . Dunque un contatore Cherenkov può
essere usato come il dispositivo di soglia per indicare la presenza di
particelle con velocità superiore ad un certo valore minimo (modificabile variando n e dunque P, come visto nell’eq.59). Dunque, dato
un fascio di particelle tutte con lo stesso impulso, l’apparecchio può
essere utilizzato al fine di identificare particelle di masse differenti.
Una classe di contatori Cherenkov a soglia usa la riflessione totale
interna come un filtro alla luce.
Consideriamo una particella che attraversa normalmente una lastra relativamente sottile di materiale limitata all’esterno dall’aria.
La luce Cherenkov uscirà dal materiale solo se l’angolo Cherenkov
sarà inferiore al valore dell’angolo critico. Precisamente la particella
potrà essere rivelata se e solo se risulta verificata la relazione:
� �
� �
1
1
∗
cos
≤ θ = sin
(63)
nβ
n
Dato un fascio di particelle tutte dello stesso impulso e fissato n,
il contatore rivelerà particelle che producono radiazione Cherenkov
con velocità superiori alla soglia stabilita nell’equazione appena fornita.
35
Figure 6:
Contatore a soglia (in alto) e differenziale (in basso).
2.4 Contatori differenziali
A differenza di un contatore a soglia, un contatore differenziale
può misurare la velocità di una particella accettando radiazione
Cherenkov solo di un piccolo anello intorno ad un dato angolo θ.
Usando questo contatore è possibile ottenere un segnale solo in
presenza di una particella di una certa massa. Mentre un contatore a soglia, dato un fascio di particelle di pari impulso, stabilisce
una velocità di soglia al di sotto della quale non vengono rivelate
le particelle e le identifica, un contatore differenziale stabilisce un
range di velocità per cui vengono rivelate le particelle (più stretto
è l’intervallo più si stima con precisione la velocità della particella,
quindi la massa).
Un contatore differenziale molto semplice può essere creato utilizzando uno specchio sferico all’interno del gas radiatore, come
mostrato in Figura 6. In suddetta Figura è mostrato anche un contatore a soglia oltre che uno differenziale.
Il cono di luce creato dalla particella che attraversa il mezzo radiatore appare allo specchio come un oggetto a forma di anello situato
all’infinito. L’immagine sarà allora un anello, situato nel piano focale dello specchio, con raggio:
r = f · tgθ
36
(64)
dove f è la lunghezza focale dello specchio.
Un diaframma contenente una fessura di lunghezza �r piazzata
di fronte al fotorivelatore farà passare solo luce nel range angolare
�θ dato da (propagazione dell’errore dall’eq. 64):
�r
(65)
f
che corrisponde, fissato un certo indice di rifrazione n, ad una
risoluzione in velocità:
�θ = cos2 θ
�β
= tanθ�θ
β
(66)
Questo mostra che piccoli θ e/o �θ sono richiesti per una buona
risoluzione in velocità.
37
Capitolo 3
Rivelatori Cherenkov e Fisica
delle Alte Energie: ILC
3.1 Introduzione
L’erede naturale di LHC è L’International Linear Collider (ILC), un
futuro acceleratore di particelle lineare progettato per far collidere
elettroni e positroni. Allo stato attuale non è ancora stato deciso
il sito che ospiterà l’acceleratore. Il progetto prevede la costruzione
di due acceleratori lineari di 12 km che sfrutterebbero intensi campi
elettrici per accelerare particelle attraverso una serie di camere a
vuoto chiamate cavità. Le cavità acceleratrici superconduttive lavoreranno ad una temperatura prossima allo zero assoluto e accelereranno le particelle fino a che queste non si scontreranno al centro
della macchina. I fasci collideranno circa 14000 volte in un secondo
a energia incredibilmente alta, 500 bilioni di eV (GeV), una scala energetica dove si ci aspetta che l’origine delle masse sia svelata e dove
nuove particelle, fondamentali in cosmologia, potranno essere scoperte. E già previsto un upgrade che porterà l’energia complessiva
nel Sistema del Centro di Massa al valore di 1 TeV. L’acceleratore
dovrebbe essere 10 volte più lungo del famoso Stanford Linear Accelerator Center (SLAC), il più lungo acceleratore lineare fino ad
oggi esistente. Le particelle avranno energia e elicità ben definite
e inoltre il fondo sarà molto contenuto, consentendo così di rivelare flebili segnali di nuove particelle e magari processi fino ad ora
sconosciuti.
Gli ulimi venti anni di scoperte nel settore delle Alte Energie
hanno permesso la creazione di un quadro organico e unitario sul
mondo del microscopico. Il quadro prevede che le tre generazioni di
fermioni fondamentali appartengano al gruppo di SU (3) × SU (2) ×
U (1) e che interagiscano mediante forze di natura debole, forte ed
elettromagnetica, osservando il rispetto del principio di gauge. Secondo questo modello si crede che la massa delle particelle sia generata dalla rottura spontanea di simmetria di SU (2) × U (1), causata
38
dal bosone di Higgs, ancora da rivelare. Sembra ormai certo che il
bosone di Higgs verrà osservato per la prima volta a LHC, in luce
dell’ultima conferenza di Dicembre 2011. Una volta rivelato, sarà
necessario studiare in profondità tutta una serie di sue proprietà,
tipo l’accoppiamento alle altre particelle e lo spin, al fine di completare il quadro attuale di conoscenza. D’altro canto, la scoperta
del bosone di Higgs porrà un nuovo problema, ormai noto in letteratura come problema di gerarchia. Esso indica che possa esserci
nuova fisica alla scala del TeV. Inoltre lo Standard Model non fornisce modelli per la dark matter di cui sembra costituito circa 1/4
della massa del nostro Universo.
Il lavoro di ILC è da sempre, fin dalla fase di progetto, visto
come complementare a quello di LHC. Esistono fondamentalmente
due tipi di acceleratori: quelli lineari (come ILC) e quelli circolari
(come LHC). Gli acceleratori di particelle circolari forniscono energie
maggiori dato che le particelle possono effettuare molte rotazioni e
quindi possono acquisire molta più energia di quella ottenibile in
un accelartore lineare, in cui, una volta terminato il percorso le
particelle devono per forza collidere con il bersaglio. Gli acceleratori di particelle circolari usualmente accelerano adroni dato che
l’accelerazione di elettroni sarebbe disturbata dalla perdita della radiazione di sincrotone.
ILC rapportato a LHC fornirà un’energia relativamente ridotta,
nella migliore delle ipotesi 1/14 dell’energia di collisione di LHC.
Tuttavia, mentre in LHC l’energia viene ripartita fra tutte le componenti adroniche, in ILC l’intera energia verrà utilizzata dagli elettroni per la collisione. Inoltre, come già detto, il fondo sarà notevolmente ridotto, e dunque sarà possibile effettuare misure di precisione
delle particelle scoperte a LHC. In conclusione LHC e ILC sono due
macchine del tutto complementari.
Al fine di adempiere alla sua funzione, ILC dovrebbe avere un alto
grado di precisione nella misura di jets e particelle cariche. Dunque,
durante questa fase di progettazione, si stanno valutando tante diverse ipotesi costruttive al fine di raggiungere l’obiettivo prefissato.
In sintesi, gli obiettivi prefissati per ILC sono:
•
Misurare la massa, lo spin e le interazioni del bosone di Higgs.
•
Misurare eventuali dimensioni extra, come postulato da alcuni
modelli teorici.
39
•
Studiare nel dettaglio le particelle supersimmetiche, particelle
che potrebbero comporre la materia oscura.
•
Vidimare sperimentalmente la teoria d’unificazione totale.
In Figura 7 è mostrato scherzosamente il passaporto e la mappa delle
terre e degli oceani dell’universo quantico che si spera ILC scoprirà.
Le dimensioni delle terre sono in relazione alle fattive possibilità di
ILC di fare luce su quei “territori” quantici. Invece in Figura 8 è
mostrata la simulazione MC di un evento collisionale che si presume
verrà osservato in ILC.
3.2 I Progetti e la Struttura
Nell’agosto 2004 l’International Techonology Recommendation Panel
(ITRP) raccomandò l’utilizzo di tecnologie superconduttori per lo
sviluppo del nuovo acceleratore. Dopo la decisione, i progetti dei tre
acceleratori, il Next Linear Collider (NLC), il Global Linear
Collider (GLC) e il Teraelectonvolt Energy Superconducting
Linear Accelerator (TESLA) vennero fusi per creare un unico
progetto, ILC. L’8 Febbraio 2007 il Draft Reference Design Report
per lo sviluppo dell’ILC venne presentato. Stando a quest’ultimo, la
realizzazione dell’ILC, i prototipi, il costo del terreno, il costo dgli
scavi, il costo dei rivelatori di particelle e l’inflazione, verranno a
costare circa 6.65 miliardi di dollari. Dopo l’approvazione finale, la
realizzazione dell’impianto e dei rivelatori dovrebbe richiedere sette
anni.
Dal 2004 fisici, ingengneri e tecnici di tutto il mondo stanno collaborando al fine di disegnare 4 differenti prototipi per ILC. Sono
ormai noti in ambiente strettamente particellare come Detector Concept Studies. Essi sono:
1.
Il Global Large Detector (GLD), basato su un tracciatore a
gas.
2.
Il Large Detector Concept (LDC), basato su un grande tracciatore a gas circondato da un calorimetro granulare.
3.
Il Silicon Detector (SiD), basato su un tracciatore al Si.
4.
Il 4th Concept, l’innovativo detector per ILC.
40
”Passaporto” e “Mappa” dell’Universo Quantico che sottolineano gli scenari di scoperta di ILC (Graphical courtesy of ILC)[3].
Figure 7:
41
Figure 8:
Simulazione di un evento collisionale in ILC.
In questa tesina ci occuperemo dello studio di un calorimetro a compensazione per il 4th Concept.
In Figura 9 è schematizzata la struttura composita di ILC.
La sorgente di elettroni sarà un laser da 2 ns che emetterà elettroni tramite un fotocatodo; gli elettroni saranno accelerati a 5 GeV
da uno stadio lineare da 250 metri (Main Linac in blue in Figura
9). I positroni, i partners antimaterici degli elettroni non esistono
naturalmente sulla Terra. Per produrli saranno inviati gli elettroni
di alta energia attraverso un ondulatore, un set speciale di magneti
in cui gli elettroni sono inodotti ad emettere radiazione di sincrotone
a seguito dell’ondulazione cui sono sottoposti. E’ come se gli elettroni fossero mandati sulle “montagne russe” per diversi giri alla fine
dei quali emetteranno un fascio di fotoni. Immediatamente dopo
l’ondulatore gli elettroni vengono reindirizzati verso l’acceleratore
primario, mentre i fotoni prodotti impatteranno su una targhetta in
lega di Titanio per produrre una coppia e+ /e− . In pratica la radiazione di sincrotone produrrà un accoppiamento elettrone positrone
su una targhetta di lega di titanio. Il processo di creazione dei
positroni è mostrato schematicamente in Figura 10.
42
Figure 9:
Rappresentazione in scala dei vari acceleratori componenti ILC.
Produzione dei positroni: facendo incidere un e− contro un
materiale ad alto numero atomico si produce uno sciame di positroni
(e+ ), fotoni (γ) ed elettroni (e− ). Con l’ausilio dei magneti i positroni
vengono raccolti e guidati verso una struttura accelerante da un lato,
gli elettroni dall’altro.
Figure 10:
43
Sezione di una cavità superconduttiva di ILC, almeno stando
all’ultimo progetto. La cavità è relazionata all’uomo per avere un’idea
della scala.
Figure 11:
I positroni verranno raccolti e accelerati fino a 5 GeV da uno stadio lineare separato (Main Linac in verde in Figura 9). Ciascuno dei
due Main Linac è costituito da 8000 cavità superconduttive congiuntamente con una serie di contenitori refrigeranti al fine di realizzare
dei moduli criogenici. I moduli utilizzano elio liquido per raffreddare
le cavità a circa - 271°C. In Figura 11 è mostrato come dovrebbe
essere la sezione di una delle cavità in proporzione all’uomo, almeno
secondo l’ultimo progetto.
Appena creati, nè i bunches di elettroni nè quelli di positroni posseggono una densità sufficiente per poter produrre collisioni nel detector. Per compattare gli elettroni e i positroni in modo da rendere
probabile la collisione questi verranno fatti circolare per 0.2 secondi
in un anello circolare di 7 km di circonferenza (in Figura 9 è rappresentato in blue il Damping Ring per gli elettroni e in verde quello
per i positroni ). Ogni bunch circolerà nell’anello circa 10000 volte
in poche decine di secondi. In ciascun anello il bunch sarà forzato ad
emettere fotoni concentrando così le particelle in pacchetti da pochi
44
mm di lunghezza e da 100 �m di diametro, in pratica più sottili
di un capello umano. Dopo il Damping Ring i pacchetti verranno
reindirizzati verso il Linac che fornirà loro un’accelerazione di circa
250 GeV per pacchetto. Cinque pacchetti verranno prodotti ogni
secondo.
Viaggiando l’uno contro l’altro a velocità prossima a quella della
luce, i bunches elettronici e positronici si scontreranno con un’Energia
totale nel Sistema del Centro di Massa pari a 500 GeV. Le spettacolari collisioni saranno registrate grazie a due grandi rivelatori
di particelle, che fungeranno come due camere fotografiche pronte
a scattare numerose snapshots degli eventi collisionali. In questo
modo sarà possibile inferire la segnatura, si spera, di nuove particelle e dunque di nuova fisica.
3.3 Il 4th Concept
Molti dei processi fisici d’interesse a ILC saranno caratterizzati da
stati finali multi-jet, spesso accompagnati da leptoni carichi e/o
MET (Missing Energy Transverse) associati a neutrini o a particelle supersimmetriche più leggere. La ricostruzione della massa
invariante di due o più jets fornirà uno strumento potente per la
ricostruzione e identificazione dell’evento.
A differenza di LEP, dove i fit cinematici permettevano un’accurata
ricostruzione di massa invariante jet-jet, praticamente indipendente
dalla risoluzione energetica dei jet, a ILC questa ricostruzione di
massa invariante dei jets è strettamente legata ad un buon grado di
risoluzione energetica del calorimetro. Dei quattro concepts proposti
per ILC, tre di questi sono basati su una “Particle Flow Analysis”
(PFA), un metodo che consente di misurare con estrema precisione
l’Energia dei jets.
L’obiettivo di ILC è raggiungere una risoluzione di massa per i
�
processi W �→ q q e Z �→ qq, paragonabile alla loro larghezza natuΓW
ΓZ
rale, cioè σ�mm = 2.7% ≈ m
≈m
. Per un calorimetro tradizionale,
W
Z
una risoluzione energetica del jet di σ�EE = √ α
conduce a una
risoluzione di massa del di-jet pari a circa
E(GeV )
σ�m
= √ α
,
m
Ejj (GeV )
dove
Ejj è l’energia del sistema di-jet e α è il termine stocastico, dovuto
cioè a fluttuazioni statistiche. A ILC, le tipiche energie del sistema
di-jet saranno dell’ordine 150 - 300 GeV, suggerendo così l’obiettivo
45
σ�E
E
= √
0.3
,
E(GeV )
che è più di un fattore 2 più grande della migliore
risoluzione energetica dei jets registrata a LEP.
Anni di misure di frammentazione di jets a LEP hanno fornito
dettagliate informazioni della composizione in particelle dei jets. In
media, dopo il decadimento di una particella di breve vita, circa il
62% dell’energia dei jets è dovuta a delle particelle cariche (principalmente adroni), circa il 27% a fotoni, circa il 10% a adroni neutri
di breve vita (ad es. n oppure KL0 ) e approssimativamente l’1.5% a
neutrini. Assumendo una risoluzione calorimetrica di σ�EE = √ 0.15
E(GeV )
per i fotoni e
σ�E
E
= √ 0.55
E(GeV )
per gli adroni, si ottiene una risoluzione
energetica del jet complessiva pari a
σ�E
E
= √ 0.19
E(GeV )
.
In pratica non è tuttavia possibile raggiungere questo livello di
performance per due ragioni. Innanzitutto, particelle viaggianti a
piccoli angoli dall’asse del fascio non possono essere rivelate. In
secondo luogo, e cosa più importante, non è possibile associare perfettamente tutti i depositi energetici con le giuste particelle. Ad
esempio, se un fotone non è risolto da una cascata adronica carica,
la sua energia non è tenuta in conto. Analogamente, se parte della
casacata adronica carica è identificata come un cluster separato,
l’energia verrà contata due volte. Questa confusione degrada la ricostruzione del flusso delle particelle e a causa di essa, la risoluzione
eneretica del jet non sarà, in generale, della forma σ�EE = √ α
.
E(GeV )
L’aspetto cruciale nella ricostruzione dell’evento sarà l’abilità di
assegnare correttamente i depositi energetici calorimetrici alle giuste
particelle ricostruite. Tutto cio’ pone precise richieste alla granularità dei calorimetri elettromagnetici e adronici. Conseguentemente,
la performance del flusso di particelle è uno degli aspetti principali
nella progettazione di ILC. Va osservato che la risoluzione energetica del jet ottenuta per un particolare Concept è la combinazione
delle performance intrinseche del detector e delle performance del
software PFA.
Le Particle Flow Analysis sono pensate per connettere direttamente gli hits provenienti dal calorimetro alle particelle neutre o
cariche per completare la ricostruzione dell’evento. Infatti la PFA
richiede la ricostruzione dei quadrivettori di tutte le particelle visibili
in un evento. L’energia ricostruita del jet è la somma delle energie
individuali di ciascuna particella. Nella PFA i momenti delle par46
ticelle cariche sono misurati nei detectors di tracciamento, mentre
le misure energetiche dei fotoni e degli adroni neutri sono ottenuti
direttamente a partire dai calorimetri. Lo step cruciale nella PFA è
dunque l’assegnazione dei corretti hits calorimetrici alle particelle ricostruite richiedendo un’efficiente separazione delle contigue cascate.
Questo implica che il calorimetro non deve semplicemente misurare
l’energia della particella che lo attraversa guardando al segnale totale
lasciato dalla particella, ma esso piuttosto fornisce un’immagine 3D
delle particelle. In altri termini il calorimetro diviene così un “Tracciatore”: tutte le particelle che passano nel detector possono essere
riscostruite, particella per particella, neutra e carica, in energia e
direzione. L’unico modo per far ciò è implementare un calorimetro
√
granulare. Ciò vuol dire che ci sarà alta precisione (30%/ E), ma
anche molti canali di lettura e dunque alti prezzi di costruzione.
Il 4th Concept è il solo dei concepts che non si avvale di un PFA
per la ricostruzione dell’evento. Il calorimetro previsto nel progetto
del 4th Concept utilizza il nuovo principio del Dual Readout: si ha
una lettura separata della luce di scintillazione proveniente da tutte
le particelle, cariche e neutre, e, separatamente, della luce Cherenkov
predominantemente legata alle particelle cariche. Questa tecnica
migliora la risoluzione energetica ad un basso prezzo e le energie
misurate sono indipendenti dal tipo di particella (fotoni, elettroni,
adroni etc...).
Il 4th Concept è deliberatamente studiato e progettato per essere
semplice, composto da solo quattro componenti. Muovendosi dal
punto d’interazione verso l’esterno troviamo nell’ordine: un tracciatore al Silicio, una Time Projection Chamber (TPC), un calorimetro
Dual Readout e uno spettrometro muonico senza ferro. Fra le varie
componenti, il calorimetro e lo spettrometro sono progetti innovativi. Il Vertex Detector è lo stesso progettato dal SiD Concept e la
TPC è la stessa prevista dai GLD e LDC Concepts.
3.4 Calorimetri a Readout multiplo
L’idea principale alla base dei calorimetri a readout multiplo è la
possibilità di misurare indipendentemente quelle quantità fisiche che
fluttuano in una cascata adronica e che conducono a fluttuazioni
nella risposta energetica. Inoltre essi consentono di mediare su quelle
grandezze che non conducono a fluttuazioni nella risposta energetica.
47
Così le grandi variazioni nella frazione energetica elettromagnetica,
fem , sono misurate direttamente per mezzo della luce Cherenkov che
è principalmente sensibile agli elettroni fortemente relativistici presenti nella cascata, e le grandi fluttuazioni spaziali sono campionate
su scala millimetrica con fibre ottiche evento per evento. L’idea innovativa è che se uno strumento misura le componenti importanti
che fluttuano da cascata a cascata, non importa quanto differentemente il mezzo sensibile sul calorimetro risponderà, infatti gli effetti
di queste fluttuazioni possono essere rimossi per raggiungere un buon
grado di risoluzione energetica.
3.4.1 Il Calorimetro Adronico (HCAL)
Il 4th Concept ha proposto un calorimetro in rame costituito sia
da fibre scintillanti che Cherenkov. Le fibre scintillanti campionano
il contenuto di particella carica totale di ciascuna cascata, mentre
quelle Cherenkov campionano predominantemente la componente
elettromagnetica di ciascuna cascata elettromagnetica. In questo
modo è misurata la frazione elettromagnetica di ciascun evento.
3.4.2 Il Calorimetro Elettromagnetico (ECAL)
L’HCAL ha una risoluzione elettromagnetica aspettata di σ�EE =
√ 20%
limitata solo dalla statistica fotoelettronica. Dunque un
E(GeV )
Calorimetro elettromagnetico (ECAL) con doppia lettura (Dual Readout) è stato preso in considerazione come aggiunta. Tutto ciò condurrà a ottime risoluzioni elettromagnetiche. Sono state considerate
due possibili soluzioni:
•
una torre con pile alternate di scintillatore plastico e vetro piombo. In questo caso, il readout individuale di ciascuna pila
fornisce le due componenti della cascata lungo il profilo longitudinale
•
un singolo cristallo di tungsteno piombo. In questo caso le
due componenti sono separate da proprietà fisiche differenti
dei meccanismi di produzione della luce di scintillazione e della
luce Cherenkov.
48
Capitolo 4
Calorimetro a Compensazione
4.1 Introduzione
Il calorimetro proposto dal 4th Concept deriva dal lavoro originale
proposto negli articoli [4], [5], [6], [7] e [8]. In questi articoli è
descritto un calorimetro, ormai noto con l’acronimo di DREAM
(Dual REAdout Module), sviluppato al Texas Tech University
(TTU).
Questo calorimetro fu proposto come uno strumento per misure
d’alta precisione di singoli adroni e di jets adronici e non soggetto alle
limitazioni imposte dai calorimetri a compensazione tradizionali. Il
detector è basato su una struttura assorbitrice in rame, attrezzata
con due tipi di mezzi attivi, ognuno dei quali misura caratteristiche
indipendenti dello sviluppo della cascata. Le idee sulle quali è basato
il modello teorico sono state confermate sperimentalmente. I risultati ottenuti non solo hanno permesso un progetto consistente per
il calorimetro di ILC, ma anche per migliorare i calorimetri tuttora
esistenti. Nel seguito svilupperemo i seguenti punti:
1.
come si pensa di sfruttare il progetto di un calorimetro a compensazione per costruire un calorimetro adronico.
2.
lo studio di un modulo DREAM.
4.2 Difficoltà e caratteristiche
In Fisica delle alte Energie un detector che consente di misurare le
proprietà delle particelle per mezzo dell’assorbimento totale (calorimetro)
è ormai divenuto un problema cruciale nello sviluppo di quasi tutti
gli esperimenti. Sebbene la rivelazione di elettroni, fotoni e altre particelle che sviluppano sciami elettromagnetici può essere fatta con
alta precisione, lo stesso non è vero per particelle che interagiscono
mediante interazione forte. Le misure calorimetriche di particelle
adroniche sono state un incubo per molti anni perché:
49
•
√
bassa risoluzione energetica, tipicamente 80 − 120% E per
grandi detectors. Ci sono poche eccezioni, tipo ZEUS a DESY,
con e/h ≈ 1, utilizzando un’appropriata scelta del rapporto
sensore/assorbitore.
•
risposta non Gaussiana. Usualmente, una lunga coda nella
risposta energetica è una caratteristica dei rivelatori adronici.
•
non linearità con l’energia. La risposta calorimetrica non è
lineare con l’energia della particella incidente.
Si sono ormai comprese le ragioni che originano queste problematiche: una risposta non uguale alla componente elettromagnetica
e adronica dei depositi energetici delle cascate (e/h �= 1), la caduta
della risposta calorimetrica per adroni poco energetici nella regione
di pochi GeV; le grandi fluttuazioni nella frazione d’energia elettromagnetica da cascata a cascata; la variazione della frazione di cascata elettromagnetica media al crescere dell’energia adronica; possibili rotture fra le celle calorimetriche; la non uniforme risposta delle
celle.
Tuttavia negli anni sono state sviluppate diverse soluzioni per
cercare di trattare i problemi descritti sopra:
1.
Calorimetri a Compensazione: sono disegnati per fornire un
uguale risposta alla componente della cascata elettromagnetica
e non. In pratica sono tali che il rapporto e/h �= 1. Quindi le
fluttuazioni nella frazione energetica dovute alla componente
della cascata elettromagnetica, f em , sono eliminate già in fase
di design. Ciò può essere ottenuto in calorimetri con idrogeno
come mezzo attivo, che è molto sensibile ai neutroni soft, abbondantemente prodotti nello sviluppo della cascata adronica. Questi calorimetri richiedono una precisa calibrazione della
frazione di campionamento. Siccome la frazione di campionamento è estremamente piccola, la risoluzione energetica elettromagnetica
di tali calorimetri è in pratica limitata a circa il
√
15%/ E.
2.
Compensazione Off-line: è una tecnica applicata in mezzi con
e/h �= 1, in cui i segnali provenienti da diverse sezioni longitudinali del calorimetro sono opportunamente pesati. E’ stato
mostrato che questa tecnica introduce una serie di indesiderabili effetti collaterali [9].
50
3.
Metodo del Flusso di Energia: l’informazione proveniente del
calorimetro è opportunamente combinata con le misure provenienti da un sistema di tracciamento, al fine di migliorare la performance per i jets. Questo metodo sfrutta il fatto che la traccia
carica dei jets può essere misurata con maggiore precisione con
un sistema di tracciamento piuttosto che con un calorimetro.
Ad ogni modo l’informazione calorimetrica è comunque necessaria per tenere in conto il contributo delle particelle neutre.
Il miglioramento di questa tecnica dipende dalla granularità
del calorimetro. Un buon grado di granularità del calorimetro
dovrebbe contribuire a identificare e eliminare tutti i contributi
delle particelle cariche dal segnale complessivo del calorimetro.
Il segnale rimanente potrebbe così essere attribuito con buona
certezza alla componente neutra del jet. In un tipico ambiente
collisionale, il miglioramento in risoluzione energetica è stimato
essere circa il 30%.
4.
Misura della componente della cascata elettromagnetica: con
questa tecnica si cerca di misurare la f em , evento per evento,
attraverso il profilo spaziale dello sviluppo delle cascate. Specialmente nei detectors basati su materiale assorbitore ad alto
Z, questi profili sono molto differenti per le cascate adroniche
e elettromagnetiche e questo metodo si è rivelato molto soddisfacente se applicato a singole particelle. Tuttavia, la distinzione diviene molto complessa per i jets molto energetici,
che consistono di una collezione di fotoni e adroni che entrano
in un’area del detector di area comparabile alle dimensioni
trasverse della cascata e/o della granularità del detector.
Ormai c’è però anche un metodo alternativo per superare questi inconvenienti per i calorimetri adronici. L’idea principale alla base
di questo nuovo prototipo di calorimetro adronico a compensazione
è misurare indipendentemente quelle quantità che fluttuano in una
cascata adronica e che conducono a fluttuazioni nella risposta energetica e di mediare su quelle quantità che invece non conducono a
fluttuazioni nella risposta energetica.
Un detector che implementa tutte queste caratteristiche con grande
successo è il modulo DREAM costruito alla Texas Tech University
(TTU) e testato al CERN [4], [5], [6], [7] e [8]. Questo detector è organizzato con due tipi di mezzi attivi (fibre al quarzo e scintillanti)
51
che misurano indipendentemente le caratteristiche dello sviluppo
della cascata.
Le fibre scintillanti sono utilizzate per misurare l’energia totale
depositata dalle particelle della cascata, in modo tale da poter campionare sulla scala millimetrica le enormi fluttuazioni d’energia spaziale.
Le fibre al quarzo invece sono utilizzate per misurare la luce
Cherenkov, che è quasi sempre esclusivamente prodotta nella componente della cascata elettromagnetica (em) (inizialmente originata
dal processo π0 −→ γγ nelle cascate adroniche). Un paragone
fra i due segnali rende possibile una misura della frazione energetica trasportata dalla seconda componente della cascata, f em ,
per ciascun evento. Come risultato, gli effetti delle fluttuazioni in
questa componente, responsabili di tutti i problemi tradizionali nei
calorimetri non compensati (non linearità, bassa risoluzione energetica, funzione di risposta non gaussiana), possono essere eliminati ed
è ottenuto un notevole miglioramento delle performance di analisi
della componente adronica.
L’idea di misurare la componente elettromagnetica della cascata
adronica risale a circa venti anni fa, ma solo recentemente è stata
fattivamente realizzata nei DREAM test. In una cascata adronica
occorrono molti processi, molto spesso con complesse dipendenze di
natura nucleare. Infatti sulla scala di bassa energia coinvolta anche
gli effetti nucleari divengono significativi. L’idea di base è che se
un mezzo misura le componenti importanti che fluttuano da cascata
a cascata, non importa quanto differentemenete i mezzi sensibili
del calorimetro rispondono, infatti gli effetti di queste fluttuazioni
possono essere rimossi per avere una migliore risoluzione energetica.
4.3 Calorimetro DREAM
Il calorimetro DREAM ha le seguenti caratteristiche principali:
√
• eccellente risoluzione energetica, circa 20 − 25%/ E per i π e
i jets in un modulo con trascurabili fluttuazioni di perdita;
•
in buona approssimazione la risposta è gaussiana;
•
la risposta è lineare nell’energia di fascio adronico in un calorimetro
che è stato calibrato con solo elettroni da 40 GeV.
52
Elemento base del detector DREAM in sezione. Sono 4 × 4
mm2 di sezione trasversa di una bacchetta di rame cavo estruso lunga
2m e di circa 2.5 mm di diametro della cavità centrale. Sette fibre
ottiche (di cui quattro Cherenkov - le bianche in figura - e 3 scintillanti
- le blue in figura) di diametro di 0.8 mm ciascuna sono inserite nella
cavità centrale.
Figure 12:
Di questi tre incredibili benefici, il terzo è probabilmente il più interessante. A ILC, un detector dovrebbe essere calibrato alla Z 0 (cioè
45 GeV e+/− , �+/− e jets), ed è previsto che misuri con alta precisione l’energia di particelle e jets fino a circa 500 GeV. Questo fattore
10 di estrapolazione implica una perdita di garanzia giacchè non ci
sono fasci di test disponibili. Ad ogni modo, nel calorimetro del 4th
Concept, questa potenzialità sarà una caratteristica intrinseca del
calorimetro stesso. Questo detector sarà lineare sulla scala spaziale
del mm e le misure simultanee di energie adroniche e elettromagnetiche sono accoppiate in guisa che una calibrazione con elettroni
risulterà in una risposta energetica adronica lineare.
L’ elemento basilare di questo detector, rappresentato schematicamente in Figura 12, è una bacchetta di rame estruso (processo industriale di deformazione del materiale al fine di ottenere una sezione
costante per il pezzo), lunga 2 m e 4×4−mm2 in sezione trasversale.
53
Questa bacchetta è cava con il cilindro centrale con diamtero di
2.5 mm. Nella cavità sono inserite sette fibre. Tre di queste sono
fibre scintillanti plastiche mentre le altre quattro sono non drogate.
Queste ultime sono utilizzate per la rivelazione della luce Cherenkov
e dunque, da adesso in poi, ci riferiremo ad esse definendole fibre
Cherenkov. Nel modulo DREAM sono stati testati due diversi prototipi di fibre Cherenkov. Per la regione centrale del detector sono
state utilizzate fibre di quarzo ad elevata purezza, laddove per le
zone periferiche del detector sono state utilizzate fibre di plastica
acrilica, che sono circa un fattore 20 meno costose. Tutte le fibre
hanno un diametro di 0.8 mm e sono lunghe 2.5 m. Il prototipo
delle fibre è lo stesso per tutte ed è quello mostrato in Figura 12.
Il detector DREAM consiste di 5580 di queste bacchette di cui
5130 riempite con fibre. Le bacchette vuote sono utilizzate come
riempitivo nelle zone periferiche del detector. Il volume strumentale
complessivo risulta quindi lungo 2.0 m e di raggio effettivo pari a
16.2 cm con una massa di 1030 kg.
La composizione della parte strumentale del calorimetro è la
seguente: 69.3% del volume del detector consiste di materiale assorbitore (rame), mentre le fibre scintillanti e Cherenkov occupano
il 9.4% e il 12.6% rispettivamente. L’aria conta per il restante 8.7%.
Nota la perdita energetica specifica di una particella a minimo di
ionizzazione (mip) nel rame (12.6 MeV/cm) e nel poliestere (2.00
MeV/cm), la frazione di campionamento della struttura Rame/Fibre
scintillanti per le mip è stata testata essere circa 2.1%.
Le fibre sono raggruppate per formare 19 torri. Ogni torre consiste di circa 270 bacchette e ha un contorno approssimativamente
esagonale (80 mm apice - apice). Il layout è schematicamente mostrato
in Figura 13. Una torre centrale è circondata da due anelli esagonali, un anello Interno (6 torri) e uno esterno (12 torri). Le torri non
sono segmentate longitudinalmente. La profondità della struttura
in rame è 200 cm o 10.0 λint . Le fibre poste nel retro di questa struttura sono separate in due bunches: un bunch di fibre scintillanti e
un bunch di fibre Cherenkov per ogni torre, 38 bunches in totale.
Questo bunch è collegato attraverso 2 mm di interstizio d’aria al
tubo fotomoltiplicatore (PMT).
In Figura 14 è mostrato il detector assemblato. Nella Figura
14.a è possibile vedere i bunches di fibre che fuoriescono dal retro
del calorimetro e i 38 PMTs utilizzati per rivelare i loro segnali.
54
Layout del detector DREAM. Il detector consiste di 19 torri
esagonali. Una torre centrale è circondata da due anelli esagonali,
l’anello Interno (6 torri) e quello Esterno (12 torri). Le torri non sono
segmentate longitudinalmente.
Figure 13:
In totale il detector contiene circa 90 km di fibre ottiche. Nella
Figura 14.b è mostrata la zona frontale del calorimetro con le fibre
illuminate da una luminosa lampada posta sul retro. La struttura
esagonale è chiaramente visibile.
Con questo tipo di calorimetro sono state raggiunte ottime performance calorimetriche. Le fibre Cherenkov campionano predominantemente la componente elettromagnetica di ogni cascata adronica e
le fibre scintillanti campionano il contenuto di particella carica totale di ogni cascata. In questo modo la frazione elettromagnetica
(EM) è misurata per ciascun evento. Le misure per ogni evento di
fascio corrispondono al segnale Cherenkov (C) contato per mezzo del
suo segnale fotoelettronico (pe) con una precisione statistica di 18
pe/GeV e il segnale di scintillazione (S) contato con una precisione
statistica di 200 pe/GeV. Le fibre Cherenkov e quelle scintillanti
sono mischiate attraverso il volume assorbitore, e così uno può pensare al modulo DREAM come a due calorimetri separati, ciascuno
calibrato indipendentemente con un fascio di elettroni da 40 GeV.
4.4 Risoluzione energetica adronica
La risoluzione energetica misurata del DREAM per π− da 200 GeV
è mostrata in Figura 15.a e corrisponde a una risoluzione in energia
55
Il detector DREAM: a) bunches di fibre uscenti dal retro del
detector, b) struttura frontale con il retro illuminato da una sorgente
brillante. Risulta molto visibile la struttura esagonale del detector.
Figure 14:
di:
σ�(E)
≈ 14%
(67)
E
che include la grande fluttuazione nella frazione EM in aggiunta
alle fluttuazioni delle perdite pari a circa il 4%.
Per ridurre lo spread energetico dovuto alla frazione EM, fem ,
sia S che C sono combinati per misurare fem evento per evento. Il
rapporto componente elettromagnetica/adronica per ciascuna componente risulta essere approssimativamente:
�e�
≡ ηC ≈ 5
(68)
h C
�e�
≡ ηS ≈ 1.4
(69)
h S
e le risposte energetiche all’energia della cascata adronica possono
essere scritte direttamente per la componente Cherenkov come:
�
�
1 − fem
C = fem +
E
(70)
ηC
56
a) Distribuzione del segnale di scintillazione S per π− di 200
GeV. Tipica risoluzione che un calorimetro a campionamento scintillante riporterebbe. b) Distribuzione d’energia calcolata a partire dalle
equazioni 70 e 71 utilizzando solo i segnali S e C per ogni evento.
Questo risultato tiene conto di fluttuazioni di perdita di circa il 4% che
contribuiscono alla risoluzione. c) Distribuzione energetica utilizzando
un’energia di fascio nota (200 GeV) per fare una migliore stima di f em
evento per evento, sopprimendo gli effetti delle fluttuazioni dovute a
perdite.
Figure 15:
57
e per la componente di scintillazione si ha:
�
�
1 − fem
S = fem +
E.
ηS
(71)
Quindi la frazione elettromagnetica, fem , può essere facilmente
estratta dai dati scrivendo l’equazione 70 in questo modo:
�
�
C
1
1
=
+ fem 1 −
,
(72)
E
ηC
ηC
e poiché η1 ≈ 0.2, il segnale Cherenkov per eventi con attività
C
EM pari a 0 conta per circa il 20% dell’energia della cascata. Ciò è
immediatamente visibile in Figura 16 dove per fem = 0 l’intercetta
C
si ha a 40 GeV, corrispondente ad un rapporto E
≈ 0.2.
Il segnale Cherenkov è dunque ampiamente correlato con
la fem . Per ogni evento di fascio, sono stati misurati C e S, e le
funzioni di risposta nelle equazioni 70 e 72, possono essere risolte
per fem e per Ecascata , fornendo la migliore stima di E. L’energia
della cascata stimata, Ecascata , è troppo bassa e fluttua di circa il
4%. In effetti, la frazione elettromagnetica calcolata dall’equazione
72 risulta:
�
�
��
ηC
C
1
fem ≈
−
(73)
Ecascata ηC
ηC − 1
fluttua del 4% giacchè il denominatore Ecascata fluttua della stessa
quantità. Sostituendo la stima della fem nell’equazione 71, la risoluzione
energetica migliora dal 14% fino a:
σ�E
≈ 5.1%
(74)
E
Questa stima include ancora fluttuazioni di perdite laterali del
4% in fem .
Ad ogni modo, al fine di ottenere la migliore stima teorica per
la risoluzione energetica, in questa fase di test del fascio è possibile perfino ottenere una migliore stima di fem per ciascun evento,
calcolando fem come:
�
��
�
ηC
C
1
fem ≈
−
(75)
Ef ascio ηC
ηC − 1
58
Altezza del impulso Cherenkov medio vs fem per jets
d’interazione a 200 GeV. Si noti che per fem = 0, il segnale Cherenkov
è circa il 20%, ossia, per attività elettromagnetica nulla in una cascata
adronica, il 20% della luce Cherenkov viene dai π+/− , K+/− e p. Per
fem = 1, il segnale Cherenov è quasi pari all’Energia della cascata.
Figure 16:
59
dove il denominatore non fluttua e, infatti, è esatto. Tutto ciò
effettivamente elimina gli effetti delle fluttuazioni dovute
alle perdite. Ciò nonostante, la stima della fem data sopra è
troppo ottimistica. Infatti essa fluttua solo a causa della fotostatistica di C, senza tenere in conto alcuna fluttuazione statistica dovuta
a Ecascata e quindi fornisce un ottimo risultato allorquando sostituita
nell’equazione 71. Ciò è evidente in Figura 15.c dove la risoluzione
energetica migliora dal 5.1% a :
σ�E
≈ 2.2%
(76)
E
Vale la pena di sottolineare che l’E f ascio è stata introdotta solo
per fare una migliore stima della f em evento per evento. La cascata
primaria e le fluttuazioni sono ancora contenute in S e in C.
Introducendo analiticamente la risoluzione della cascata, le fluttuazioni per la fissata energia di fascio risultano in una risoluzione
di:
σ�E
≈ 3.2%.
(77)
E
La risoluzione energetica di questo modulo dual-readout, in assenza di fluttuazioni di perdita, non è nota sperimentalmente, ma
presumibilmente è compresa fra 2.2% e 5.1% per π− di 200 GeV.
Partendo dai fit a tutte le energie, risulta che questo modulo ha un
termine costante pari a circa il 2%, verosimilmente dovuto a piccoli effetti, quasi tutti controllabili. Per “jets d’interazione” queste
risoluzioni sono le stesse o leggermente migliori. Ciò è mostrato nei
fits di Figura 17.
Il modulo test DREAM non è stato progettato e disegnato per
produrre la migliore risoluzione energetica possibile, ma piuttosto
per essere una prima prova dell’effettivo successo dell’idea che è
alla base del modulo DREAM. Chiaramente una fluttuazione delle
perdite, nota e attesa, pari a circa il 4%, limiterà drasticamente la
risoluzione energetica, ma non inficerà la valutazione della tecnica
del dual read-out.
In Figura 17 è mostrata la risoluzione energetica per singoli π− e
jets per tutte le energie di fascio testate sperimentalmente. E’ chiaro
che questa tecnologia calorimetrica scala bene come √1E e con un termine costante relativamente piccolo, sebbene ci siano miglioramenti
in fase di progettazione.
60
I dati relativi alle varie scale energetiche testate per i π−
e i jets d interazione mostrano un perfetto scaling della risoluzione
energetica del tipo √1E . La frazione elettromagnetica è stata calcolata
��
�
�
ηC
C
con la relazione: fem ≈ Ef ascio
− η1
.
η −1
Figure 17:
�
C
61
C
4.5 Risoluzione energetica elettromagnetica
Il modulo DREAM è stato inoltre esposto ad un fascio elettronico
da 20 a 200 GeV e, poiché le fibre scintillanti e quelle Cherenkov
sono ugualmente sensibili alle cascate elettromagnetiche, le funzioni di risposta sono essenzialmente le stesse. Ad ogni modo, la
risoluzione Cherenkov è limitata da una bassa statistica fotoelettronica, laddove la luminosità di scinitllazione è un fattore 20 più
grande. La risoluzione energetica del DREAM è mostrata in Figura
18, in cui le fibre scintillanti
misurano una risoluzione energetica su√
periore di 20.5%/ E + 1.5%. La misura Cherenkov è indipendente
da quest’ultima. Una misura migliore potrebbe dunque essere fatta
combinando queste due misure.
Le cascate elettroniche nel modulo DREAM sono molto strette
e depositano circa il 92% di Energia in ciascuna cella. Quindi gli
elettroni possono essere identificati dalla loro stretta profondità e
dalla richiesta S ≈ C.
62
Risoluzione energetica elettronica per fibre Cherenkov e di
scintillazione separatamente. La risoluzione energetica finale può essere
leggermente migliorata eseguendo una combinazione dei due segnali.
Ciò non è tuttavia ancora stato fatto.
Figure 18:
63
Conclusioni
Il calorimetro proposto dal 4th Concept per ILC sarà un potenziamento nonché un miglioramento del modulo DREAM già testato
ed esposto per sommi capi in questo lavoro di tesina.
Sono al vaglio ulteriori possibili suggerimenti che potrebbero favorire un certo miglioramento delle prestazioni calorimetriche. Ossia:
•
ogni fibra sarà inserita nella propria cavità consentendo così un
aumento notevole della statistica DREAM e riducendo la correlazione nei segnali di multi-fibra (sia per quelle Cherenkov che
per quelle di scintillazione) dovuti al passaggio di una singola
traccia.
•
la geometria di un singolo modulo potrebbe essere una piramide
rettangolare con la sommmità troncata ( “piramide rettangolare
monca”). Questo tipo di geometria fornirebbe un mosaico senza
possibili fratture far i vari moduli ed è stata studiata per essere
compatibile con una geometria cilindrica del tracciatore e della
bobina.
E’ inoltre sotto studio il progetto di una sezione di cristallo EM
di fronte a questo calorimetro a multiple-readout. Esso stesso sarà
dual-readout, in modo da ottenere due benefici: una crescita della
statistica fotoelettronica per le cascate elettromagnetiche e una migliore
risoluzione spaziale per i fotoni.
Il progetto del 4th Concept prevede la costruzione di due moduli
che sfruttino questi ulteriori suggerimenti, oltre al principio di funzionamento del modulo DREAM, e che diverranno proprio moduli
operativi di ILC. I test ulteriori saranno effettuati al FERMILAB.
64
Bibliografia
[1] V.P. Zrelov Cherenkov Radiation in High-Energy Physics.
[2] Arnold Sommerfeld Lectures on Theoretical Physics, Vol.IV:Optics.
[3] www.linearcollider.org
[4] “Hadron and Jet Detection with a Dual-Readout Calorimeter”,
N. Akchurin, et al., Nucl. Instrum. and Methods A537
(2005) 537-561.
[5] “Electron Detection with a Dual-Readout Calorimeter”, N.
Akchurin, et al., Nucl. Instrum. and Methods A536 (2005)
29-51.
[6] “Muon Detection with a Dual-Readout Calorimeter”, N. Akchurin,
et al., Nucl. Instrum. and Methods A533 (2004)
305-321.
[7] “Comparison of Scintillation and Cˇerenkov Light in Highenergy Electromagnetic Profiles”, N. Akchurin, et al., Nucl.
Instrum. and Methods
A548 ( 2005) 336-354.
[8] “Separation of Scintillation and Cˇerenkov Light in an Optical
Calorimeter”, N. Akchurin, et al., Nucl. Instrum. and
Methods A 550 (2005)
185-200.
[9] M. Albrow et al. , Nucl. Instr. and Meth. in Phys. Res.
A487 (2002) 381.
[10] Vito di Benedetto, “Study of a Compensating Calorimeter
for a e+ e− Linear Collider at Very High Energy”.
[11] Francesco Cirotto, Marco Mirra, Giuseppe Ferone, Nello Bruscino, “Effetto Cherenkov e sue applicazioni”, Tesina di Elettrodinamica Classica.
65