AE1 - ESERCIZI

(6(5&,=,
$5&+,7(7785$'(*/,(/$%25$725,DD
±/(,6758=,21,0(72',',,1',5,==$0(172
– /(,6758=,21,
1.
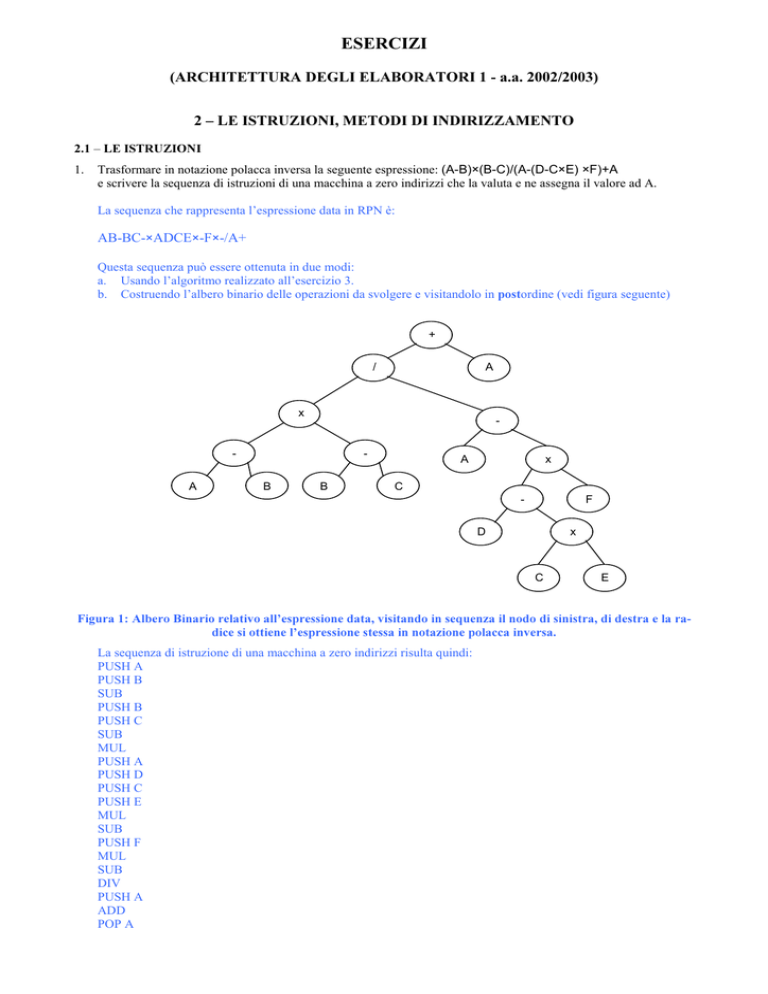
Trasformare in notazione polacca inversa la seguente espressione: (A-B)×(B-C)/(A-(D-C×E) ×F)+A
e scrivere la sequenza di istruzioni di una macchina a zero indirizzi che la valuta e ne assegna il valore ad A.
La sequenza che rappresenta l’espressione data in RPN è:
AB-BC-×ADCE×-F×-/A+
Questa sequenza può essere ottenuta in due modi:
a. Usando l’algoritmo realizzato all’esercizio 3.
b. Costruendo l’albero binario delle operazioni da svolgere e visitandolo in SRVWordine (vedi figura seguente)
+
/
A
x
-
A
B
B
A
x
C
-
F
D
x
C
E
)LJXUD$OEHUR%LQDULRUHODWLYRDOO¶HVSUHVVLRQHGDWDYLVLWDQGRLQVHTXHQ]DLOQRGRGLVLQLVWUDGLGHVWUDHODUD
GLFHVLRWWLHQHO¶HVSUHVVLRQHVWHVVDLQQRWD]LRQHSRODFFDLQYHUVD
La sequenza di istruzione di una macchina a zero indirizzi risulta quindi:
PUSH A
PUSH B
SUB
PUSH B
PUSH C
SUB
MUL
PUSH A
PUSH D
PUSH C
PUSH E
MUL
SUB
PUSH F
MUL
SUB
DIV
PUSH A
ADD
POP A
2.
Utilizzando le direttive assembly, definire le aree di memoria che contengono (vedi T4, pg. 160 – 162);
ƒ il vettore V di 80 elementi lunghi 32 bit,
V: .DS% 80*4 ;
ƒ la matrice M di 5 righe e 8 colonne, con elementi di 16 bit,
M: .DS% 5*8*2 ;
ƒ il vettore V5 di 5 elementi di 8 bit, contenenti, nell’ordine, i primi 5 numeri dispari (1, 3, 5, 7, 9),
V5: .DC% 1,3,5,7,9 ;
ƒ il vettore S5 contenente i codici ASCII dei primi 5 numeri dispari,
S5: .DC% 49,51,53,55,57 ;
ƒ il vettore S contenente la stringa ‘Auguri di buona Pasqua!’.
S: .DCB ‘Auguri di buona Pasqua!’,0
3.
progettare, in pseudocodice o in JAVA, un algoritmo che trasformi una stringa contenente un’espressione aritmetica tradizionale (con priorità degli operatori e parentesi e con operandi rappresentati da singoli caratteri) in una
stringa contenente una equivalente espressione in notazione polacca inversa;
[suggerimento: si scandiscano i caratteri della stringa in input:
ƒ se si incontra uno spazio, lo si ignora,
ƒ se si incontra un operando, lo si ricopia subito nella costruenda stringa di output,
ƒ se si incontra un operatore o una parentesi, lo si inserisca (push) in uno stack temporaneo;
la decisione di quando estrarre (pop) da questo stack temporaneo l’ultimo elemento inserito (per trasferirlo nella
stringa di output, se è un operatore; per buttarlo via perché non serve più ,se è una parentesi), sarà basata
sull’esame del carattere successivo nella stringa di output: si costruisca una tabella che contempli tutti i casi che
possono presentarsi e la si utilizzi nella codifica dell’algoritmo.]
[Vedi http://www.dei.unipd.it/corsi/ae1/RPN.java]
– 0(72',',,1',5,==$0(172
1.
Calcolare il numero di accessi alla memoria effettuati ad ogni iterazione del ciclo di pg 145;.
MOVB
MOVB
LOOP MOVW
ADDW
MOVW
ADDL
SUBB
JNZ
#100,R2 ;
#0,R2 ;
300(R1),R0 ;
500(R1),R0 ;
R0,100(R1);
#2,R1;
#1,R2;
LOOP;
fetch(OL) + fetch(EL)
=2
fetch(OL) + fetch(EL)
=2
fetch(OL) + fetch(EL) + VAL (L) = 3
fetch(OL) + fetch(EL) + VAL (L) = 3
fetch(OL) + fetch(EL) + VAL (S) = 3
fetch(OL) + fetch(EL)
=2
fetch(OL) + fetch(EL)
=2
fetch(OL) + fetch(EL)
=2
_____________
= 19 ACCESSI
2.
Definire, con le apposite direttive assembly, un’area di memoria di 4096 byte da usare come stack e scrivere le istruzioni assembly del PD32 con cui si realizzano le operazioni di push e di pop su di esso (vedi T4, pg. 164 –
165);
STL = 4096
.DSB STL
ST:
.DSB 1
MOVL #ST,R7
MOVL R0, -(R7) ; R7 – 4 , R0 -> L[R7] - OPERAZIONE DI PUSH
MOVL (R7)+, R1 ; L[R7] -> R1, R7 + 4 - OPERAZIONE DI POP
3.
Definire, con le apposite direttive assembly due vettori A e B contenenti entrambi 100 elementi di 4 byte ciascuno;
scrivere quindi un segmento di programma che inserisca nell’elemento B[i] del vettore B la somma dei primi i+1
elementi del vettore A. (B[0]=A[0], B[1]=B[0]+A[1], … B[i]=B[i-1]+A[i],…)
N = 100
L = 4
A:
.DSB
B:
.DSB
MOVEL
MOVL
MOVL
MOVEL
LOOP: ADDL
MOVL
ADDL
SUBL
JNZ
N*L
N*L
A, B
#N-1, R2
#L, R1
B, R0
A(R1),R0
R0, B(R1)
#L,R1
#1, R2
LOOP
; A[0] -> B[0] (primo caso trattato a parte)]
; contatore (N-1 iterazioni: tutti gli elementi meno il primo)
; l’offset dei secondi elementi (A[i] e B[1]) nel registro indice R1
; B[0] in R0, per sommarvi A[1] la I volta (B[i]=B[i-1]+A[i], con i=1)
; B[i-1] + A[i] -> R0
; … -> B[i]
; i++
; contatore -; contatore = 0 ?
4.
Supponendo che il processore PD32, dal quale vengono eseguite le istruzioni del ciclo iterativo di pg.145, abbia un
clock da 600 MHz, che ogni accesso alla memoria richieda 4 cicli di clock, che ciascuna delle istruzioni del ciclo
richieda, per la sua esecuzione, un ciclo di clock ulteriore rispetto a quelli necessari per gli accessi alla memoria,
calcolare i il tempo impiegato dal PD32 per eseguire una iterazione e quello complessivo per sommare i 2 vettori.
Il numero di accessi alla memoria necessari per ogni singola istruzione è già stato calcolato nell’esercizio 1; tenendo conto delle ipotesi poste, si può ora calcolare il numero di cicli occorrenti per l’esecuzione delle stesse .
MOVB
MOVB
LOOP MOVW
ADDW
MOVW
ADDL
SUBB
JNZ
#100,R2 ;
#0,R2 ;
300(R1),R0 ;
500(R1),R0 ;
R0,100(R1);
#2,R1;
#1,R2;
LOOP;
fetch(OL) + fetch(EL)
fetch(OL) + fetch(EL)
fetch(OL) + fetch(EL) + VAL (L)
fetch(OL) + fetch(EL) + VAL (L)
fetch(OL) + fetch(EL) + VAL (S)
fetch(OL) + fetch(EL)
fetch(OL) + fetch(EL)
fetch(OL) + fetch(EL)
= 2 -> 4*2 +1= 9
= 2 -> 4*2 +1= 9
= 3 -> 4*3 +1= 13
= 3 -> 4*3 +1= 13
= 3 -> 4*3 +1= 13
= 2 -> 4*2 +1= 9
= 2 -> 4*2 +1= 9
= 2 -> 4*2 +1= 9
Pertanto avremo:
ciclo iterativo: 66
*
iterazioni
100
=
totale
6600
+
inizializzazione 18
=
totale cicli
6618
Quindi, considerando che 1 ciclo del clock del processore dura 1 / FHz = 1 / (600 * 106) = 1, 667 ns, il tempo complessivo è pari a 6618 * 1,667 ns = 11.032,206 ns = 11,032 µs
5.
Con riferimento alla fig. 4.9 (T4, pg. 149), supponendo che si vari tra siMIN = -10 V e siMAX = +10 V,
− calcolare il valore digitale corrispondente ai seguenti valori di si: 3.5 V, -3.5 V, 1 V, -1 V;.
Il valore digitale prodotto sarà proporzionale al valore del segnale rilevato pertanto avremo che:
•
•
•
•
32.767 : 10V = X : 3,5V quindi X = (32.767 * 3,5)/10 = 11.468,45 che, convertito in binario con 16bit e
rappresentato in esadecimale, viene approssimato con &&&;
eA = |Valore Reale – Valore Discretizzato| = |3,5 - ((11.468 *10 )/32.767)| = 0.14 mV
eR = ( eA / Valore Reale) * 100 = (0.14 mV / 3,5 * 103 mV ) * 100 = 0.004 %
32.767 : 10V = X : -3,5V quindi X = (32.767 * -3,5)/10 = -11.468,45 che con 16bit in complemento a 2
viene approssimato con ';
eA = |Valore Reale – Valore Discretizzato| = |-3,5 - ((-11.468 *10 )/32.767)| = 0.14 mV
eR = ( eA / Valore Reale) * 100 = (0.14 mV / 3,5 * 103 mV ) * 100 = 0.004 %
32.767 : 10V = X : 1V quindi X = (32.767 * 1)/10 = 3.276,7 che con 16bit viene approssimato con
&&';
eA = |Valore Reale – Valore Discretizzato| = |1 - (( 3.277*10 )/32.767)| = 0.09 mV
eR = ( eA / Valore Reale) * 100 = (0.09 mV / 1 * 103 mV ) * 100 = 0,009 %
32.767 : 10V = X : 1V quindi X = (32.767 * -1)/10 = -3.276,7 che con 16bit in complemento a 2 viene
approssimato con );
eA = |Valore Reale – Valore Discretizzato| = |-1 - (( -3.277*10 )/32.767)| = 0.09 mV
eR = ( eA / Valore Reale) * 100 = (0.09 mV / 1 * 103 mV ) * 100 = 0,009 %
− calcolare il valore di tensione si corrispondente al seguente valore digitale: $8A00;
Per considerazioni analoghe alle precedenti abbiamo che:
$8A00 in complemento a 2 corrisponde a –30.20810 e quindi 32.767 : 10V = -30.208 : X
X = (-30.208*10)/32.767 = 9
− calcolare l’errore assoluto di discretizzazione in mV e quello relativo.
6.
Con riferimento alla fig. 4.10 (T4, pg. 150), supponendo che il periodo di clock sia T = 100 µs, indicando con t0 e
ti gli istanti in cui si verifica il fronte di salita di due impulsi successivi del segnale START, si valuti il campo di
variabilità dell’intervallo d = ti – t0 tale da garantire che i due impulsi di START provochino due conversioni in
corrispondenza di due impulsi di clock successivi [suggerimento: deve essere d = T = 100 µs];
d<T
T
d
COMPLE TE
START
CLOCK
d>T
d
COMPLE TE
START
CLOCK
1
2
3
4
5
6
Affinché vengano rispettate le specifiche richieste (due impulsi START tali da provocare due conversioni in due
clock successivi) deve essere che d = ti – t0 = T = 100 µs perché:
• Se d < T (primo caso in figura) avremo che i segnali di START si susseguirebbero troppo velocemente e
otterremo delle situazioni come quella presentata nel periodo 2 dove il primo dei due segnali verrebbe
“perso”
• Se d > T (secondo caso in figura) invece otterremo che avremo fronti di salita del clock in cui non effettueremo conversioni come ad esempio al termine del periodo 3
7.
Con riferimento al codice riportato in T4, pg. 158 e alla fig. 4.12 (T4, pg 159), supponendo che il tempo di conversione tc dei 5 convertitori sia compreso tra 1 µs e 1.2 µs, e nell’ipotesi che il tempo di esecuzione delle istruzioni
del PD32 (comprese le operazioni di fetch) sia di 84 ns per le istruzioni la cui codifica occupa 1 longword, 150 ns
per quelle da 2 longword, 217 ns per quelle da 3 longword, si calcoli il periodo minimo TMIN del clock che garantisce la contemporaneità dei campioni acquisiti e la non perdita di dati.
>YHGL(VHUFL]LSUHSDUDWRULDOSULPRFRPSLWLQR6ROX]LRQHGHOO¶HVHUFL]LR@
Prima che sia trascorso un periodo del clock, il processore deve fare in tempo a completare l’acquisizione dei 5
campioni e a comandare l’acquisizione dei 5 successivi; deve, cioè, completare l’esecuzione di tutte le istruzioni
comprese tra V1: … e JMP V1
Qui sotto è riportato il tempo di esecuzione di ciascuna di esse.
Va tenuto inoltre presente il fatto che le istruzioni di attesa (Vx: JNR Adx, Vx) sono destinate ad essere eseguite
più volte, in attesa che, trascorso il tempo di conversione, il dato sia pronto.
&RQVLGHUD]LRQH
Per rispettare le specifiche del problema, bisogna considerare il caso peggiore che si ha quando il primo dei dispositivi che vengono esaminati dal programma (AD1) è il più lento (ha un tempo di conversione pari a 1200ns).
In questa ipotesi il primo ciclo di attesa (V1: JNR AD1, V1) viene eseguito tante volte quante servono a far trascorrere i 1200ns (si tenga anche presente il fatto che, per rispettare la specifica sulla simultaneità dei 5 campioni
acquisiti, il fronte di salita che avvia le conversioni non può verificarsi prima che siano state eseguite tutte 5 le istruzioni START, quindi al più presto nel corso della esecuzione di JMP V1).
&RQVLGHUD]LRQH
Il caso più sfortunato è che, trascorso questo tempo, debba ancora iniziare il fetch della istruzione V1: JNR AD1,
V1 la cui esecuzione trova READY = 1 e consente di uscire dal ciclo di attesa. Pertanto la durata di questo primo
ciclo di attesa è, nel caso peggiore, 1200+150ns.
Sommando i tempi indicati accanto a ciascuna istruzione, si ottiene un totale di 3720ns.
Per rispettare le specifiche del problema, tra due fronti di salita del clock devono trascorrere almeno 3720ns. Questo è pertanto il valore minimo del periodo di clock richiesto.
V1: JNR AD1, V1 ;
INW AD1, TAB1(R1) ;
V2: JNR AD2, V2;
INW AD2, TAB2(R1) ;
V3: JNR AD3, V3;
INW AD3, TAB3(R1) ;
V4: JNR AD4, V4;
INW AD4, TAB4(R1) ;
V5: JNR AD5, V5;
INW AD5, TAB5(R1) ;
ADDL #2, R1 ;
SUBB #1, R0 ;
JZ FINE ;
START AD1 ;
START AD2;
START AD3;
START AD4;
START AD5 ;
JMP V1 ;
2L
2L
2L
2L
2L
2L
2L
2L
2L
2L
2L
2L
2L
1L
1L
1L
1L
1L
2L
1200+150ns
150ns
150ns
150ns
150ns
150ns
150ns
150ns
150ns
150ns
150ns
150ns
150ns
84ns
84ns
84ns
84ns
84ns
150ns