Correnti e circuiti a corrente continua

Correnti e circuiti a corrente
continua
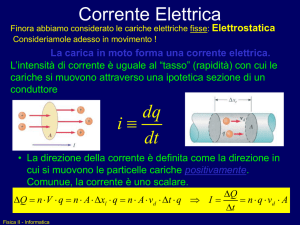
La corrente elettrica
Corrente elettrica: carica che
fluisce attraverso la sezione di un
conduttore in una unità di tempo
∆Q
I=
∆t
Intensità di corrente media
∆Q dQ
I = lim
=
∆t →0 ∆t
dt
Intensità corrente istantanea
Unità di misura nel S.I.: ampere (A)
1 A equivale al passaggio della carica di 1 C attraverso
una superficie in un’unità di tempo di 1 s
1C
1A =
1s
Verso della corrente elettrica: per convenzione il
verso attribuito alla corrente elettrica è opposto al
moto degli elettroni.
I
In un conduttore ordinario (es. filo di rame) la corrente è
dovuta al moto degli elettroni (carica negativa).
Nei gas e liquidi (es. soluzione elettrolitica) la corrente
è il risultato del moto sia delle cariche positive che di
quelle negative (vd. elettrolisi)
Dal punto di vista microscopico:
q: carica di ciascun portatore
n: densità di portatori di
carica (numero di portatori
per unità di volume)
V: volume dell’elemento
di conduttore:
V=
∆Q: carica mobile
A ⋅ ∆x
∆Q = (n ⋅ V ) ⋅ q = (n ⋅ A ⋅ ∆x ) ⋅ q
vd: velocità di deriva. Velocità media dei
portatori di carica all’interno del conduttore
∆x
vd =
∆t
Dal punto di vista microscopico:
∆Q: carica mobile
∆Q = (n ⋅ V ) ⋅ q = (n ⋅ A ⋅ ∆x ) ⋅ q
∆Q = (n ⋅ A ⋅ ∆x ) ⋅ q = (n ⋅ A ⋅ vd ⋅ ∆t ) ⋅ q
Dividendo ambedue i membri per l’intervallo di tempo si
ottiene la corrente media:
∆Q
I=
= n ⋅ A ⋅ vd ⋅ q
∆t
Espressione della corrente media in
funzione dei parametri microscopici
Densità di corrente (J): corrente che
circola nel conduttore per unità di
area. Unità di misura nel S.I. :
ampere su metro-quadrato
I
J ≡ = n ⋅ vd ⋅ q
A
Velocità di deriva:
Si è definita come velocità media dei portatori di carica
(elettroni) lungo il conduttore (filo elettrico). Ciò non vuol
dire che gli elettroni si muovono in linea retta.
In assenza di una differenza di
potenziale il moto è casuale, simile a
quello delle molecole di un gas (vd.
modello della teoria cinetica dei gas).
Le velocità medie degli elettroni nel
conduttore sono dell’ordine di 106 m/s
Sotto l’azione di un campo elettrico, gli elettroni sono
soggetti ad una forza e vengono accelerati, originando la
corrente elettrica. Il moto dovuto alla forza elettrica si
sovrappone al moto casuale e il risultato è una velocità
media il cui modulo è la velocità di deriva.
Velocità di deriva: esempio
Un filo di rame con sezione di area 3.31 x 10-2 cm2 trasporta una
corrente di 10 A. Calcolare la velocità di deriva assumendo che
vi è un elettrone libero di conduzione per ciascun atomo di Cu.
(Densità del Cu: 8.95 g/cm3; massa molare del Cu: 63.5 g/mol)
∆Q
I=
= n ⋅ A ⋅ vd ⋅ q
∆t
I
vd =
n ⋅ A⋅ q
Volume occupato da una mole (da 63.5 g):
63.55 g / mol
3
V=
=
=
7
.
09
cm
/ mol
3
8.95 g / cm
ρ
M
In una mole vi sono un numero di atomi (e quindi per ipotesi
anche un numero di elettroni di conduzione) pari al numero di
Avogadro (6.02 x1023 atomi)
Velocità di deriva: esempio
Un filo di rame con sezione di area 3.31 x 10-2 cm2 trasporta una
corrente di 10 A. Calcolare la velocità di deriva assumendo che
vi è un elettrone libero di conduzione per ciascun atomo di Cu.
(Densità del Cu: 8.85 g/cm3; massa molare del Cu: 63.5 g/mol)
La densità di elettroni liberi è quindi pari a:
6.02 ⋅10 23 elettroni / mole
23 elettroni
0
.
85
10
n=
=
⋅
3
3
cm
7.09 cm / mole
I
10 C / s
vd =
=
n ⋅ A ⋅ q 0.85 ⋅10 23 cm −3 ⋅ 3.31⋅10 − 2 cm 2 ⋅1.6 ⋅10 −19 C
I
− 2 cm
−4 m
vd =
= 2.22 ⋅10
= 2.22 ⋅10
Molto bassa!
n⋅ A⋅ q
s
s
Velocità di deriva: esempio
Un filo di rame con sezione di area 3.31 x 10-2 cm2 trasporta una
corrente di 10 A. Calcolare la velocità di deriva assumendo che
vi è un elettrone libero di conduzione per ciascun atomo di Cu.
(Densità del Cu: 8.85 g/cm3; massa molare del Cu: 63.5 g/mol)
I
−4 m
vd =
= 2.22 ⋅10
n ⋅ A⋅ q
s
∆x
Tempo impiegato per percorrere 1m:
vd =
∆t
∆x
1m
∆t =
=
≈ 4504 s ≈ 75 min
−4
v d 2.22 ⋅10 m / s
Ad essere pressoché istantaneo è il campo elettrico che si
stabilisce nel conduttore. E’ per questo che la luce si
accende subito quando si preme l’interruttore.
Dal punto di vista energetico:
Durante il passaggio di corrente elettrica in un conduttore si
ha una trasformazione di energia:
Energia chimica della batteria
Energia potenziale del campo elettrico
necessario a far circolare corrente
Energia cinetica degli elettroni
Energia termica trasferita al sistema a seguito dei continui
urti degli elettroni in moto con gli atomi del metallo
Correnti e circuiti a corrente
continua
Resistenza elettrica e legge di Ohm
Applicando una differenza di
potenziale ∆V ai capi di un conduttore
metallico si origina un campo elettrico,
responsabile del moto degli elettroni e
quindi della corrente. ∆V = E ⋅ l
La velocità di deriva degli elettroni è direttamente proporzionale
al campo elettrico (vedi poi).
Allora la corrente che circola nel conduttore (che si è visto
essere proporzionale alla velocità di deriva) risulta
direttamente proporzionale alla differenza di potenziale
applicata. La costante di proporzionalità prende il nome di
resistenza del conduttore.
∆V
R≡
I
Unità di misura nel S.I.: Ohm (Ω
Ω).
Se la differenza di potenziale di 1V ai capi di un
conduttore determina una corrente di 1A, allora la
resistenza del conduttore è pari a 1 Ω
Resistenza: esempio
Quanto vale la resistenza di un conduttore metallico in cui
circola una corrente di 6 A sotto l’azione di una differenza
di potenziale pari a 120V?
∆V 120V
R≡
=
= 20 Ω
I
6A
Cosa ne è della resistenza se si raddoppia la differenza di
potenziale ai capi del conduttore?
R resta costante: raddoppiando ∆V raddoppierà anche
l’intensità di corrente, ma il rapporto (resistenza) resta
costante.
Questo è vero per i conduttori Ohmici, per i quali cioè la
resistenza resta costante in un grande intervallo di tensioni.
Legge di Ohm:
Dalla definizione di resistenza elettrica si ha:
∆V = I ⋅ R
Per i conduttori Ohmici (i metalli)
vale la legge di Ohm. La corrente
cresce linearmente con la
tensione in un ampio intervallo.
Esistono anche dispositivi che
non seguono la legge di Ohm.
Un esempio è il diodo,
dispositivo a semiconduttore
caratterizzato da una curva
corrente-tensione non lineare.
Resistenza, resistività e conducibilità:
La resistenza di un filo conduttore ohmico è proporzionale alla
lunghezza del filo ed inversamente proporzionale alla sua
sezione:
l
R= ρ⋅
A
La costante di proporzionalità ρ prende il nome di resistività.
Unità di misura nel S.I.: Ohm per metro (Ω
Ω⋅m).
Il reciproco della resistività è definita come conducibilità:
La resistenza, espressa in
funzione della conducibilità è:
1 l
R= ⋅
σ A
σ=
1
ρ
Un elemento circuitale che fornisce una specifica resistenza
all’interno di un circuito elettrico è detto resistore. Il simbolo
in un diagramma circuitale è una linea a zig-zag.
R
La resistività (e quindi anche la conducibilità) varia molto a
seconda della particolare sostanza. A temperatura ambiente
(20°C) i buoni conduttori (argento, rame, oro, alluminio,
tungsteno, ferro) hanno una resistività dell’ordine di 10-8 Ω⋅m.
Un isolante come il vetro è caratterizzato da una resistività
molto più alta, dell’ordine di 1010-1014 Ω⋅m
Resistività vs. Temperatura
e
Superconduttori
Variazione della resistività con la temperatura
La resistività dipende dalla temperatura.
Per molti metalli in un intervallo limitato di
temperature, la resistività aumenta
linearmente con la temperatura secondo
la legge:
ρ = ρ ⋅ +α ⋅( − )
0
[1
T T0
]
ρ0: resistività alla temperatura di
riferimento T0 (20°C)
α: coefficiente termico della resistività
Essendo la resistenza direttamente proporzionale alla resistività,
la variazione della resistenza con la temperatura è esprimibile
come:
Questa proprietà può essere
R = R0 ⋅ [1 + α ⋅ (T − T0 )] usata per ottenere misure precise
di temperatura.
Esiste una classe di metalli e composti per i quali la resistenza
diminuisce bruscamente al di sotto di una particolare
temperatura critica Tc. Essi sono noti come superconduttori
La resistività dei superconduttori al di
sotto di Tc sono inferiori a 4x10-25 Ω⋅m
(ricordiamo che i buoni conduttori hanno
resistività dell’ordine di 10-8 Ω⋅m)
L’interesse è ricercare materiali con
comportamento di superconduttore a Tc
relativamente alte.
Al
1.19 K ; -271.96°C
HgBa2Ca2Cu3O8
134 K ; -139.15°C
Un modello strutturale per la
corrente elettrica
Abbiamo già introdotto un modello che lega la corrente elettrica
alle grandezze microscopiche del conduttore
I = n ⋅ A⋅v ⋅ q
d
Cerchiamo ora di spiegare l’origine microscopica della resistenza
Ipotesi del modello:
1) Energia cinetica degli elettroni → energia vibrazionale degli
atomi del conduttore → riscaldamento del conduttore
2) Moto dell’elettrone dopo l’urto indipendente dal suo moto
prima dell’urto
L’elettrone è accelerato dalla forza elettrica e tra due urti si
muove di moto uniformemente accelerato
r
r
r
r Fe − eE
r r r
r eE
=
v = v0 + a ⋅ t = v0 −
⋅t
a=
me
me
me
r r r
r
v = v0 + a ⋅ t = v0 −
r
eE
me
⋅t
Il moto dell’elettrone è caratterizzato da
un grande numero di urti al secondo.
Consideriamo quindi il valore medio della velocità su un intervallo
lungo rispetto al tempo tra due collisioni, che corrisponde proprio
alla velocità di deriva
Le velocità iniziali sono distribuite casualmente lungo le varie
direzioni (per l’ipotesi 2) quindi il valor medio di v0 è zero
Carica, campo elettrico e massa sono costanti quindi il solo
fattore che influenza la media è il tempo
r
eE
r
r r
Dove τ è il tempo medio fra gli urti
vd = v0 + a ⋅ t = −
⋅τ
me
Velocità di deriva proporzionale al
campo elettrico
I = n ⋅ A ⋅ vd ⋅ q
r
vd = −
r
eE
⋅τ
me
Sostituendo l’espressione trovata per la velocità di deriva si ha:
e⋅ E
ne 2 E
I = n ⋅ A ⋅ vd ⋅ e = n ⋅ A ⋅
⋅τ ⋅ e =
⋅ A ⋅τ
me
me
Considerando inoltre la legge di Ohm, il legame resistenzaresistività, e il legame differenza di potenziale-campo elettrico
in un conduttore si ha:
∆V ∆V
E ⋅l
E
I=
=
⋅A=
⋅A= ⋅A
R
ρ ⋅l
ρ ⋅l
ρ
Eguagliando le due espressioni della corrente e risolvendo
per la resistività si ottiene:
ne 2 E
E
m
I=
⋅ A ⋅τ = ⋅ A → ρ = 2e
me
ρ
ne τ
Modello classico
me
ρ= 2
ne τ
lmed
τ=
v med
Libero cammino medio
Velocità media
E’ possibile usare questa espressione per calcolare la
resistività dei conduttori che obbediscono alla legge di Ohm.
Ci sono delle problematiche:
-I valori teorici sono inferiori a quelli reali di circa un fattore 10
-La resistività dovrebbe variare con la temperatura come la
velocità media che, in accordo con il modello dei gas perfetti,
è proporzionale a T
Tali limitazioni si superano migliorando il modello tenendo
conto dei fenomeni quantistici (carattere ondulatorio degli
elettroni): modello quantomeccanico
Correnti e circuiti a corrente
continua
Energia e potenza elettrica
L’energia chimica fornita dalla batteria viene trasferita al
resistore. Calcoliamone l’espressione:
Si immagini di seguire una carica Q positiva che si muove
lungo il circuito:
- parte dal punto a con potenziale nullo (riferimento),
- attraversa la batteria acquistando un’energia potenziale
elettrica pari a U=Q·∆V (a discapito dell’energia chimica della
batteria),
- si muove da b a c senza perdere energia (supponendo trascurabile la resistenza
del filo)
- attraversa il resistore perdendo energia a seguito delle collisioni con gli atomi
del resistore (trasformazione in energia interna al resistore associata ai moti
vibrazionali) aumento di temperatura del resistore (effetto Joule)
- ritorna in a senza ulteriore perdita di energia (filo di R trascurabile)
La variazione nel tempo dell’energia potenziale elettrica è quindi:
dU d (Q∆V ) dQ
=
=
⋅ ∆V = I ⋅ ∆V
dt
dt
dt
dU d (Q∆V ) dQ
=
⋅ ∆V = I ⋅ ∆V
=
dt
dt
dt
Tale variazione nel tempo dell’energia potenziale
elettrica rappresenta la potenza fornita al resistore:
P = I ⋅ ∆V
Questa espressione è valida per qualsiasi dispositivo che trasporti una
corrente I e avente una differenza di potenziale ∆V ai suoi capi
Ricordando inoltre la legge di Ohm:
∆V = I ⋅ R
si ha:
P = I2 ⋅R
P = I ⋅ ∆V
2
(
∆V )
P=
Unità di misura nel S.I.: Watt (W)
R
1 W è la potenza che in 1 s produce l’energia di 1 J.
Un’unità di misura pratica per l’energia è il chilowattora, che è l’energia
fornita dalla potenza di 1 kW per 1h:
3
6
1 kWh = 10 W ⋅ 3600 s = 3.6 ⋅10 J
Energia e potenza elettrica: esempi
Si considerino le due lampadine in figura. Quale ha resistenza
maggiore? Quale trasporta una corrente maggiore?
La potenza fornita a ciascuna lampadina dipende
dalla resistenza:
2
(
∆V )
P=
R
la lampadina con resistenza minore
assorbirà una potenza maggiore. RA > RB
Dalla legge di Ohm si ricava inoltre che la
corrente attraverso la lampadina B sarà maggiore
che in A
In quale caso è più probabile che una lampadina “bruci”? Al
momento dell’accensione o quando è accesa già da un po’?
Al momento dell’accensione il filamento della lampadina è freddo e quindi la sua
resistenza è bassa. Di conseguenza la corrente che circola è alta (così pure la
potenza fornita) e può portare alla rottura del filamento.
Via via che la lampadina è accesa il filamento si riscalda e quindi la sua
resistenza elettrica aumenta e corrente e potenza fornita diminuiscono
Energia e potenza elettrica: esempi
Per una comune lampadina di 60 W funzionante a 220 V
A) trovare la corrente nella lampadina e la sua resistenza
B) calcolare quanto costa tenere accesa la lampadina per 24 ore
considerando un costo dell’elettricità pari a 0.11 €/kWh
A) La sigla 220V /60 W significa che la lampadina ha una tensione di
funzionamento di 220 V ed una potenza di 60 W.
La corrente che attraversa la lampadina si ricava dall’espressione della potenza:
P = I ⋅ ∆V ⇒ I =
P
60W
=
≅ 0.273 A
∆V 220V
La resistenza si ottiene dalla legge di Ohm:
∆V 220V
∆V = I ⋅ R ⇒ R =
=
≅ 807 Ω
I
0.27 A
Energia e potenza elettrica: esempi
Per una comune lampadina di 60 W funzionante a 220 V
A) trovare la corrente nella lampadina e la sua resistenza
B) calcolare quanto costa tenere accesa la lampadina per 24 ore
considerando un costo dell’elettricità pari a 0.11 €/kWh
B) La lampadina ha una potenza di 60 W=0.060 kW, per cui il costo di
funzionamento per 24 ore è:
Euro
costo = 0.06 kWh ⋅ 24 h ⋅ 0.11
= 0.158 Euro
kWh
Correnti e circuiti a corrente
continua
Sorgenti di f.e.m.
(“forza elettromotrice”)
L’elemento che mantiene costante la differenza di potenziale
in un circuito è detto sorgente di f.e.m. (forza elettromotrice).
Tipici esempi sono batterie, pile, alimentatori.
La f.e.m. ε di una sorgente esprime il lavoro svolto per unità di
carica. L’unità di misura nel S.I. è quindi il volt (non è una forza!)
La f.e.m. della batteria non coincide con la
differenza di potenziale ai capi della batteria. La
batteria possiede infatti una resistenza interna r
che comporta una piccola caduta di tensione:
∆V = ε − I ⋅ r
∆V = I ⋅ R
I=
ε
R+r
Da cui si osserva che la corrente nel circuito dipende sia dalla
resistenza esterna (di carico) R, sia dalla resistenza interna r.
Se r << R si può comunque considerare
ε
∆V
I= =
R
R
In termini di potenza:
I=
ε
R+r
ε = I ⋅R + I ⋅r
I ⋅ε = I 2 ⋅ R + I 2 ⋅ r
moltiplicando per I si ottiene:
Cioè la potenza totale erogata dalla sorgente di f.e.m. si
ripartisce tra il resistore e la batteria stessa
Se r<<R la maggior parte della potenza è fornita alla resistenza di carico
Se r>>R la maggior parte della potenza rimane all’interno della sorgente di f.e.m.
(esempio: collegamento dei capi di una pila con del filo elettrico riscaldamento
della batteria)
Correnti e circuiti a corrente
continua
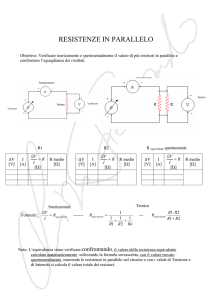
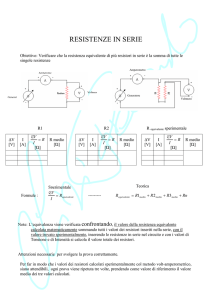
Resistori in serie e in parallelo
Resistori (resistenze) in serie
Due resistori sono collegati in serie
quando hanno un estremo in comune
La corrente che circola nei due
resistori è la stessa I = I = I
1
2
La differenza di potenziale fornita dalla
batteria si ripartisce tra i due resistori
∆V = ∆Vab + ∆Vbc
∆Vab = I ⋅ R1
∆V = I ⋅ (R1 + R2 )
Essendo
∆Vbc = I ⋅ R2
si ha:
Resistori (resistenze) in serie
∆V = I ⋅ (R1 + R2 )
∆V = I ⋅ Req
Si può pensare al circuito come costituito
da una sola resistenza equivalente, pari
alla somma delle due singole resistenze.
Generalizzando la resistenza equivalente
di un insieme di n resistori collegati in
serie è uguale alla somma delle singole
resistenze.
Req = R1 + R2 + K + Rn
In un collegamento in serie la resistenza equivalente è
sempre maggiore di ciascuna singola resistenza
Resistori (resistenze) in parallelo
Due resistori sono collegati in parallelo quando
hanno entrambi gli estremi in comune
Ciascun resistore è collegato direttamente
ai capi della batteria e quindi la differenza di
potenziale ai capi dei resistori è la stessa
∆V = ∆V1 = ∆V2
La corrente totale che circola si ripartisce
nei due resistori I = I + I
Essendo
1
∆V = I1 ⋅ R1
∆V = I 2 ⋅ R2
2
si ha:
1
1 
∆V ∆V
I = I1 + I 2 =
+
= ∆V ⋅  + 
R1
R2
 R1 R2 
Resistori (resistenze) in parallelo
1
1 
∆V
I = ∆V ⋅  + 
I=
Req
 R1 R2 
Si può pensare al circuito come costituito da
una sola resistenza equivalente, legata alle
singole resistenze dalla relazione:
1
1
1
= +
Req R1 R2
R1 ⋅ R2
Req =
R1 + R2
Generalizzando il reciproco della resistenza
equivalente di un insieme di n resistori
collegati in parallelo è uguale alla somma dei
reciproci delle singole resistenze.
In un collegamento in parallelo la resistenza equivalente è
sempre minore della più piccola resistenza del circuito
Resistenze in serie e in parallelo: esempio
A.
B.
Trovare la resistenza equivalente tra a e c.
Qual è la corrente che passa in ciascun
resistore se viene mantenuta una differenza
di potenziale di 42 V tra a e c?
Resistenze in serie e in parallelo: esempio
A.
B.
Trovare la resistenza equivalente tra a e c.
Qual è la corrente che passa in ciascun
resistore se viene mantenuta una differenza
di potenziale di 42 V tra a e c?
A) I due resistori da 8 Ω e 4 Ω sono collegati in
serie, e quindi la resistenza equivalente tra a e b
è pari a: 8+4= 12 Ω.
I due resistori da 6 Ω e 3 Ω sono collegati in
parallelo, e quindi la resistenza equivalente tra b
e c è pari: 6x3/(6+3)=18/9=2 Ω
Le due resistenze calcolate sono in serie, quindi
la resistenza equivalente è pari a 12+2 =14 Ω
Resistenze in serie e in parallelo: esempio
A.
B.
Trovare la resistenza equivalente tra a e c.
Qual è la corrente che passa in ciascun
resistore se viene mantenuta una differenza
di potenziale di 42 V tra a e c?
B) Essendo la resistenza equivalente pari a 14 Ω e la
differenza di potenziale 42 V, la corrente si ricava
dalla legge di Ohm come:
∆V 42V
I=
=
=3A
Req 14 Ω
Questo è la corrente che circola tra a e b e quindi nei resistori di 8 Ω
e 4 Ω. Nel nodo b la corrente si divide tra le due resistenze in
parallelo. Qui vale:
∆Vbc = I1 ⋅ 6 Ω = I 2 ⋅ 3 Ω

 I1 + I 2 = 3 A
Da cui:
 I 2 = 2 I1
I 2 = 2 A
⇒

 I1 + 2 I1 = 3 A  I1 = 1 A
Resistenze in serie e in parallelo: esempio
Tre resistori sono collegati in parallelo. Tra i punti a e b viene
mantenuta una differenza di potenziale di 18 V.
A. Trovare la corrente che passa in ciascun resistore
B. Calcolare la potenza fornita a ciascun resistore e la potenza
totale fornita ai tre resistori
C. Calcolare la resistenza equivalente dei tre resistori
A) I tre resistori sono collegati in parallelo e ai capi di ciascuno di essi
la differenza di potenziale è di 18 V. Dalla legge di Ohm si ottiene:
∆V 18V
∆V 18V
∆V 18V
I
=
=
=2A
3
I1 =
=
=6A
I2 =
=
=3A
R3
9Ω
R
3Ω
R
6Ω
1
2
B) Sapendo che P = I 2 ⋅ R per ciascun resistore si ha:
2
P1 = I12 ⋅ R1 = (6 A) ⋅ 3 Ω = 108W
2
P2 = I 22 ⋅ R2 = (3 A) ⋅ 6 Ω = 54 W
2
P3 = I 32 ⋅ R3 = (2 A) ⋅ 9 Ω = 36W
Ptot = P1 + P2 + P3 = 198W
Resistenze in serie e in parallelo: esempio
Tre resistori sono collegati in parallelo. Tra i punti a e b viene
mantenuta una differenza di potenziale di 18 V.
A. Trovare la corrente che passa in ciascun resistore
B. Calcolare la potenza fornita a ciascun resistore e la potenza
totale fornita ai tre resistori
C. Calcolare la resistenza equivalente dei tre resistori
C) I tre resistori sono collegati in parallelo, vale quindi:
1
1
1
1
= +
+
Req R1 R2 R3
1
1
1
1
11
=
+
+
=
Req 3 Ω 6 Ω 9 Ω 18 Ω
18 Ω
Req =
= 1.64 Ω
11
Lo stesso risultato di può ottenere dalla legge di Ohm considerando la
differenza di potenziale tra a e b e la corrente totale (somma delle tre
correnti):
∆V
18V
Req =
=
= 1.64Ω
I tot 6 A + 3 A + 2 A
Elettrolisi e costante di
Faraday
Cella elettrolitica: soluzione elettrolitica + due elettrodi
Passaggio di corrente nella soluzione: moto degli ioni positivi e negativi →
spostamento di materia verso gli elettrodi
La massa delle sostanze liberate agli elettrodi è proporzionale alla carica
elettrica che ha attraversato la cella e, per ogni elemento, al rispettivo
equivalente chimico (rapporto tra peso atomico M e valenza z)
Al catodo: se Q è la carica che attraversa la cella, il numero n di ioni
positivi, di valenza z che migrano al catodo è:
Q
n=
z ⋅e
(dove e = 1.602 ⋅10 −19 C )
M
23
−1
m
=
(
dove
N
=
6
.
022
⋅
10
mol
)
La massa mi di ciascuno ione:
i
Avo
N Avo
La massa totale trasportata e depositata al catodo è quindi:
m = n ⋅ mi =
Q M
⋅
z ⋅ e N Avo
m=
Q⋅M
z⋅F
F = e ⋅ N Avo = (96485.3399 ± 0.0024) C ⋅ mol −1 Costante di Faraday
Esercizi corrente
Un tostapane assorbe 600 W quando è collegato a una tensione di 220 V. Quale
corrente attraversa il tostapane e qual è la sua resistenza?
2
P = I ⋅ ∆V = I
2
(
∆V )
⋅R =
R
P
600W
P = I ⋅ ∆V ⇒ I =
=
= 2.7 A
∆V 220V
∆V = I ⋅ R
∆V 220V
∆V = I ⋅ R ⇒ R =
=
= 81Ω
I
2.7 A
Si consideri il circuito in figura. Trovare la resistenza equivalente tra i punti a e b.
Se una differenza di potenziale di 34 V è applicata tra i punti a e b , calcolare la
corrente in ogni resistore.
R2=7 Ω
La resistenza equivalente delle due
resistenze in parallelo R2 ed R3:
R4=9 Ω
R1=4 Ω
1
1
1
17
=
+
=
R23 7 Ω 10 Ω 70 Ω
70 Ω
R23 =
= 4.12 Ω
17
R3=10 Ω
a
Complessivamente si hanno ora tre resistenze in serie.
La resistenza equivalente totale:
Req = R1 + R23 + R4 = ( 4 + 4.12 + 9) Ω = 17.12 Ω
b
Si consideri il circuito in figura. Trovare la resistenza equivalente tra i punti a e b.
Se una differenza di potenziale di 34 V è applicata tra i punti a e b , calcolare la
corrente in ogni resistore.
R2=7 Ω
Essendo la resistenza equivalente pari
a 17.12 Ω e la differenza di potenziale
34 V, la corrente si ricava dalla legge
di Ohm come:
∆V
34V
I=
=
= 1.98 A
Req 17.2 Ω
R4=9 Ω
R1=4 Ω
R3=10 Ω
a
Questa è la corrente che circola in R1 ed R4.
Nel nodo dopo R1 la corrente si divide tra R2 ed R3. Essendo R2 ed R3
collegate in parallelo, vale:
 I 2 ⋅ 7 Ω = I 3 ⋅10 Ω

 I 2 + I 3 = 1.98 A
Da cui:
 I 2 = 1.16 A

 I 3 = 0.82 A
b
Si consideri un costo dell’elettricità di 0.12 Euro per kWh. Calcolare il costo:
a) Per una lampada da 40 W lasciata accesa per due settimane
b) Per l’uso per tre minuti di un tostapane di 970 W
c) Per il lavaggio di un carico di vestiti per 40 minuti in una lavatrice di 5200 W
a)
Euro
costo = 40 ⋅10 kW ⋅ (2 ⋅ 7 ⋅ 24) h ⋅ 0.12
= 1.62 Euro
kWh
b)
3
Euro
costo = 970 ⋅10 kW ⋅ h ⋅ 0.12
= 5.8 ⋅10−3 Euro
60
kWh
−3
c)
−3
40
Euro
costo = 5.2 kW ⋅ h ⋅ 0.12
= 0.42 Euro
60
kWh
La Capacità e i circuiti RC
Un condensatore consiste di due conduttori di
forma qualsiasi elettricamente isolati l’uno
dall’altro e da mezzo in cui sono contenuti. Una
volta che il condensatore è stato caricato i due
conduttori portano cariche uguali ed opposte
La differenza di potenziale ai capi del
condensatore è direttamente proporzionale
alla carica del condensatore (definita come la
carica presente su una delle due armature)
La costante di proporzionalità prende il
nome di capacità:
Q
C≡
∆V
Unità di misura
nel S.I.: farad (F).
farad =
coulomb
volt
CARICA DI UN CONDENSATORE
Alla chiusura del circuito circola corrente che porta all’accumulo di carica sulle
armature del condensatore. Il processo si arresta quando il condensatore è
completamente carico.
q
ε = + IR
C
dq Cε − q
=
dt
RC
q dq
ε= + R
C dt
dq ε
q
= −
dt R RC
Equazione differenziale: separo le
variabili (carica e tempo) e integro
CARICA DI UN CONDENSATORE
dq Cε − q
=
dt
RC
Equazione differenziale: separo le variabili (carica e tempo)
e integro
q
dq
1
=−
dt
q − Cε
RC
dq
1
∫0 q − Cε = − RC ∫0 dt
t
 q − Cε 
ln
=
−

RC
 − Cε 
−
q − Cε
= e RC
− Cε
t
t
t
−


RC
q(t ) = Cε ⋅ 1 − e 


Andamento temporale della carica presente
sulle armature del condensatore
Il valore massimo della carica è Cε per
t →∞
Il parametro τ (dimensioni di un tempo) è
detto costante di tempo del circuito RC
CARICA DI UN CONDENSATORE
t
−


RC
q(t ) = Cε ⋅ 1 − e 


Differenziando l’espressione si ricava l’andamento temporale della
corrente nel circuito RC:
dq
I (t ) =
dt
I (t ) =
ε
R
⋅e
−
t
RC
ε
Il valore massimo della corrente, per t=0 è
R
SCARICA DI UN CONDENSATORE
Prima della chiusura del circuito il condensatore è
completamente carico. Una volta chiuso il circuito
inizia a circolare corrente. Sia la carica che la corrente
diminuiranno esponenzialmente con il tempo
dq q
−R
=
dt C
q
+ IR = 0
C
dq
1
=−
dt
q
RC
q
t
ln  = −
RC
Q
Differenziando l’espressione si
ricava l’andamento temporale della
corrente nel circuito RC:
q
t
dq
1
∫Q q = − RC ∫0 dt
q(t ) = Q ⋅ e
t
−
t
RC
t
−
Q − RC
⋅e
= − I 0 ⋅ e RC
I (t ) = −
RC
Si considerino i seguenti parametri del circuito RC di un defibrillatore: C=32 uFe
R=47kΩ. Per caricare il circuito di applica una differenza di potenziale di 5000 V.
Trovare la costante di tempo del circuito, la massima carica del condensatore, la
massima corrente nel circuito durante il processo di carica e la carica e corrente in
funzione del tempo
τ = RC = 47 ⋅103 Ω × 32 ⋅10−6 F = 1.5 s
Q = C ⋅ ε = 32 ⋅10−6 F × 5000V = 0.160 C
ε
5000V
I0 = =
= 0.106 A
3
R 47 ⋅10 Ω

q(t ) = 0.160 C ⋅ 1 − e

t
−
1.50 s




I (t ) = 0.106 A ⋅ e
−
t
1.50 s