Document

Sommario
•
Le Variabili Casuali o Variabili
Aleatorie
Corso di Statistica
Facoltà di Economia
a.a. 2010
2010--2011
francesco mola
Lezione n° 13
Lez.13_a.a. 20109-2011
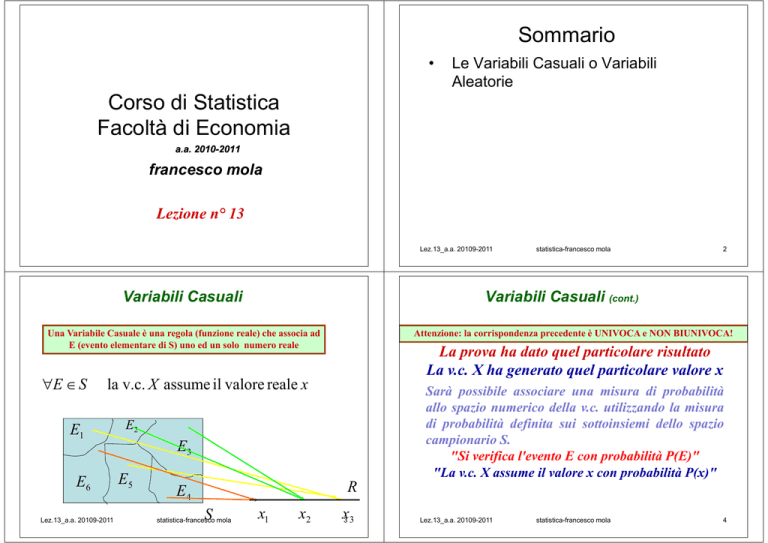
Variabili Casuali
Attenzione: la corrispondenza precedente è UNIVOCA e NON BIUNIVOCA!
La prova ha dato quel particolare risultato
La v.c. X ha generato quel particolare valore x
la v.c. X assume il valore reale x
E1
E6
Lez.13_a.a. 20109-2011
Sarà possibile associare una misura di probabilità
allo spazio numerico della v.c. utilizzando la misura
di probabilità definita sui sottoinsiemi dello spazio
campionario S.
"Si verifica l'evento E con probabilità P(E)"
"La v.c. X assume il valore x con probabilità P(x)"
E2
E3
E5
2
Variabili Casuali (cont.)
Una Variabile Casuale è una regola (funzione reale) che associa ad
E (evento elementare di S) uno ed un solo numero reale
∀E ∈ S
statistica-francesco mola
R
E4
S
statistica-francesco mola
x1
x2
x3 3
Lez.13_a.a. 20109-2011
statistica-francesco mola
4
Variabili Casuali (cont.)
Variabili Casuali
1
p3
Una v.c. X è una variabile che assume valori nello spazio
dei numeri reali secondo una funzione di probabilità P(X).
E2
E1
E3
E6
E5
p2
R
E4
x1
S
Lez.13_a.a. 20109-2011
statistica-francesco mola
5
Esempio:consideriamo una famiglia con 3 figli
E1
E2
E3
E4
E5
E6
E7
E8
S={MMM,MMF,MFM,FMM,MFF,FMF,FFM,FFF}
1/8
1/8
1/8
1/8
1/8
1/8 1/8 1/8
Lez.13_a.a. 20109-2011
X
0
1
2
3
x2
p1
0
x3
statistica-francesco mola
6
Px
0.125
0.375
0.375
0.125
1
Definiamo la variabile casuale X=“ numero dei figli maschi”
{E8 }
{E5 ∪ E6 ∪ E7 }
{E2 ∪ E3 ∪ E4 }
{E1}
Lez.13_a.a. 20109-2011
X
0
1
2
3
statistica-francesco mola
0.375
pi
1/8
3/8
3/8
1/8
E1
E2
E3
E4
0.125
E5
7
E6
Lez.13_a.a. 20109-2011
E7
E8
0
statistica-francesco mola
1
2
3
8
X
0
1
Consideriamo come esempio due variabili: Titolo di studio e
condizione occupazionale
A =titolo di studio
E= elementare
M= media
S= superiore
B=condizione occupazionale
O= occupato
D= inoccupato
Px
0.5
0.5
1
EO
Possiamo definire i seguenti possibili eventi elementari.
MO
S= A*B= {EO, ED, MO, MD, SO, SD}
1/6 1/6 1/6 1/6 1/6 1/6
SO
Dato l’insieme S è possibile da cui derivare diverse variabili casuali
ED
0.5
MD
SD
Consideriamo la variabile casuale X= “ condizione occupazionale”
X = {1
o
occupato
inoccupato
Lez.13_a.a. 20109-2011
statistica-francesco mola
X
0
1
Px
0.5
0.5
9
Sempre partendo da S consideriamo la variabile casuale
Y=“ studi superiori”
0
Y =
1
Y
Py
0 0.667
1 0.3333
S
ED
MD SO
Event p(E)
i
1
0.33
0
Lez.13_a.a. 20109-2011
statistica-francesco mola
1
statistica-francesco mola
10
Esempio: lancio di un dado, di una moneta, estrazione di un
numero al lotto (a k eventi sono associati k valori della V.C.)
MO
SD
Lez.13_a.a. 20109-2011
0
Schematicamente
0.66
EO
0
1
0
11
V.c.X
px
E1
E2
p1
p2
x1
x2
p x1
p x2
E3
⋮
Ek
p3
⋮
pk
x3
⋮
xk
p x3
⋮
p xk
Lez.13_a.a. 20109-2011
statistica-francesco mola
12
Tipi di variabili casuali
Schematicamente
V.C.
Esempio: #figli, condizione occupazionale. Ecc.
(a k eventi sono associati h<k valori della V.C.)
Eventi
p(E) V.c.X
E1
E2
p1
p2
E3
⋮
Ek
p3
⋮
pk
Lez.13_a.a. 20109-2011
px
x1
x2
⋮
p x1
p x2
⋮
xh
p xh
con h ≠ k
Discrete
(S,A,p) = spazio di
probabilità e A è
l’insieme di tutti gli
eventi generabili da
S con l’unione e la
negazione
statistica-francesco mola
13
In natura
Continue
discretizzate
Lez.13_a.a. 20109-2011
statistica-francesco mola
14
Una variabile casuale discreta può
essere
rappresentata graficamente
variabili casuali discrete
Una Variabile Casuale è nota se
conosciamo la sua distribuzione di probabilità
pi
Le x possono essere arbitrarie, mentre le probabilità
non possono essere arbitrarie perché:
∀i = 1, ⋯ , k
 pi ≥ 0

∑ pi = 1

Lez.13_a.a. 20109-2011
statistica-francesco mola
x1
15
Lez.13_a.a. 20109-2011
x2
x3
statistica-francesco mola
xi
16
Variabili Casuali continue
f(x)
Attenzione, f(x) non è
la probabilità!!!!!!
• Ammette infiniti valori, quindi non è
possibile attribuire le singole probabilità
ad ogni x.
• Si associa ad ogni intervallo una
funzione f(x) detta funzione di densità.
X
_ f(x)
è proporzionale (a meno di un infinitesimo) alla
probabilità di un intervallo sufficientemente piccolo
Lez.13_a.a. 20109-2011
statistica-francesco mola
17
Se X è una variabile casuale che assume valori in [a,b], essa
è definita se:
∃f ( x ) : ∀ x0 ∈ (a, b )
Esempio:
(− ∞,+∞ )
statistica-francesco mola
18
Condizione necessaria affinché una funzione di densità f(x) individui
una v.c. X continua è :
Nota bene:
con la conseguenza che la funzione di densità è nulla per
quei valori compresi in intervalli esterni al campo di
definizione!
Lez.13_a.a. 20109-2011
statistica-francesco mola
∀x : −∞ < X < +∞
 f (x ) ≥ 0
+ ∞

 ∫ f (x )dx = 1
−∞
P( x0 ≤ X ≤ xo + dx ) = f ( x0 )dx
le variabili casuali continue sono definite in
Lez.13_a.a. 20109-2011
19
P( X = x0 ) =
Lez.13_a.a. 20109-2011
x0
∫ f (x )dx = 0
x0
statistica-francesco mola
20
Funzione di ripartizione
Funzione di ripartizione (proprietà)
La funzione di ripartizione fornisce la probabilità di un
qualsiasi evento
∑p
xi ≤ x
F (x ) = P( X ≤ x ) =
x
∫
statistica-francesco mola
∀xi < x j ⇒ F (xi ) ≤ F (x j )
0 ≤ F ( x) ≤ 1
2) è sempre compresa tra 0 ed 1
Variabili Casuali
Discrete
3) si ha che:
f (ω )dω
−∞
Lez.13_a.a. 20109-2011
i
1) è non decrescente
lim F ( x ) = 0
Variabili Casuali
Continue
∀x ∈ (− ∞,+∞ )
lim F ( x ) = 1
x →−∞
x → +∞
4) F ( x) è continua da destra
21
Lez.13_a.a. 20109-2011
statistica-francesco mola
22
caso X discreta
Grafico della funzione
Esempio: lancio di un dado
F(x) 1
0
Lez.13_a.a. 20109-2011
statistica-francesco mola
X
1
2
3
4
5
6
X
23
P(x)
1/6
1/6
1/6
1/6
1/6
1/6
Lez.13_a.a. 20109-2011
pi
1
1/6
1
statistica-francesco mola
2
3
4
5
6
xi
24
Analizziamo la F(X)
0 −∞ ≤ x <1
F(x)
1/ 6 1 ≤ x < 2
1
2/6 2 ≤ x < 3
5/6
3/ 6 3 ≤ x < 4
4/6 4 ≤ x < 5
5/6 5 ≤ x < 6
1 6≤ x<∞
Lez.13_a.a. 20109-2011
caso X continua
P( x0 ≤ X ≤ x1 ) = P( X ≤ x1 ) − P( X ≤ x0 ) =
= F ( x1 ) − F ( x0 ) =
4/6
3/6
2/6
∫ f ( x)dx
x0
1/6
0
1
2
statistica-francesco mola
3
4
5
6
25
graficamente
x
Lez.13_a.a. 20109-2011
F ( x)
f ( x)
statistica-francesco mola
26
graficamente
F ( x1 )
F ( x0 )
x 0 x1
Lez.13_a.a. 20109-2011
x1
Funzione
a gradini o
step function
x
statistica-francesco mola
x0
27
Lez.13_a.a. 20109-2011
x1
x
statistica-francesco mola
28
…una relazione importante
Momenti centrali
Valore medio; valore atteso; Expectation
x
F ( x) =
∫
µ = E ( X ) = ∑ xi pi
f (ω )dω
+∞
−∞
µ = E ( X ) = ∫ xf (x )dx
d
F ( x) = f ( x)
dx
Lez.13_a.a. 20109-2011
statistica-francesco mola
V.c. discrete
V.c continue
−∞
µ r = E (X
29
Momenti centrali: casi particolari
r
)= ∑ x
V.c continue
Lez.13_a.a. 20109-2011
r
i
In generale abbiamo:
pi
V.c. discrete
µ = E (X
r
statistica-francesco
mola
+∞
r
) = ∫ x f (x )dx
r
−∞
30
Momenti scarto dalla media
(x − µ )
( )
r = 0 ⇒ µ 0 = E X 0 = ∑ xi0 p i = ∑ p i = 1
r
(
)
x
−
µ
pi
∑ i
r = 1 ⇒ µ1 = E ( X ) = ∑ xi p i = µ
V.c. discrete
µr = E(X − µ ) =
r
V.c continue
+∞
r
(
)
x
−
µ
f ( x )dx
∫ i
Lez.13_a.a. 20109-2011
statistica-francesco mola
31
Lez.13_a.a. 20109-2011
−∞
statistica-francesco mola
32
Momenti scarto dalla media:
casi particolari
Momenti scarto dalla media:
casi particolari
µ1 = E ( X − µ ) = ∑ (xi − µ ) pi =
µ 2 = E ( X − µ )2 = ∑ ( xi − µ )2 pi =
(
∑x
2
i
Lez.13_a.a. 20109-2011
statistica-francesco mola
33
Momenti standardizzati
 x−µ 


 σ 
x
 X −µ 
µr = E
 =
 σ 
Lez.13_a.a. 20109-2011
r
Lez.13_a.a. 20109-2011
statistica-francesco mola
 X −µ  1
=
σ

 σ
µ1 = E 
2
V.c continue
 xi − µ 
∫−∞ σ  f (x )dx
statistica-francesco mola
µ 2 − µ 2 = σ 2 = VAR( X ) = VARIANZA
∑ (xi − µ ) pi =
1
 X −µ 
µ2 = E
 = 2
 σ  σ
V.c. discrete
+∞
pi + µ 2 ∑ pi − 2 µ ∑ xi pi = µ 2 + µ 2 − 2µ 2 =
34
Momenti standardizzati:
casi particolari
 i −µ 
∑  σ  pi
r
)
= ∑ xi2 + µ 2 − 2 µxi pi =
= ∑ xi pi − µ ∑ pi = µ − µ = 0
0
σ
∑ (xi − µ )2 pi =
=0
1
σ
2
σ
=1
2
r
35
Lez.13_a.a. 20109-2011
statistica-francesco mola
36
Momenti standardizzati: casi particolari
1
 X −µ
3
(
)
=
x
−
µ
pi =
µ3 = E 

∑
i
3
 σ  σ
1
= 3 µ 3 = γ 1 = coefficiente di asimmetria
3
σ
1
 X −µ 
µ4 = E
 = 4
 σ  σ
1
4
=
σ
4
µ4
⇒ µ4 − 3 = γ 2 =
Lez.13_a.a. 20109-2011
4
(
)
x
−
µ
pi =
∑ i
µ4
− 3 = Coefficiente di Curtosi
σ4
statistica-francesco mola
37