Document

Tecniche nel dominio delle frequenze: Assorbimento Multifotonico (1)
Spettroscopia di assorbimento multifotonico
Il processo di assorbimento multifotonico descrive l’assorbimento di più
fotoni in maniera istantanea o sequenziale da parte del mezzo materiale.
Questi processi sono processi di tipo non parametrico e quindi sono
considerati dei processi attivi.
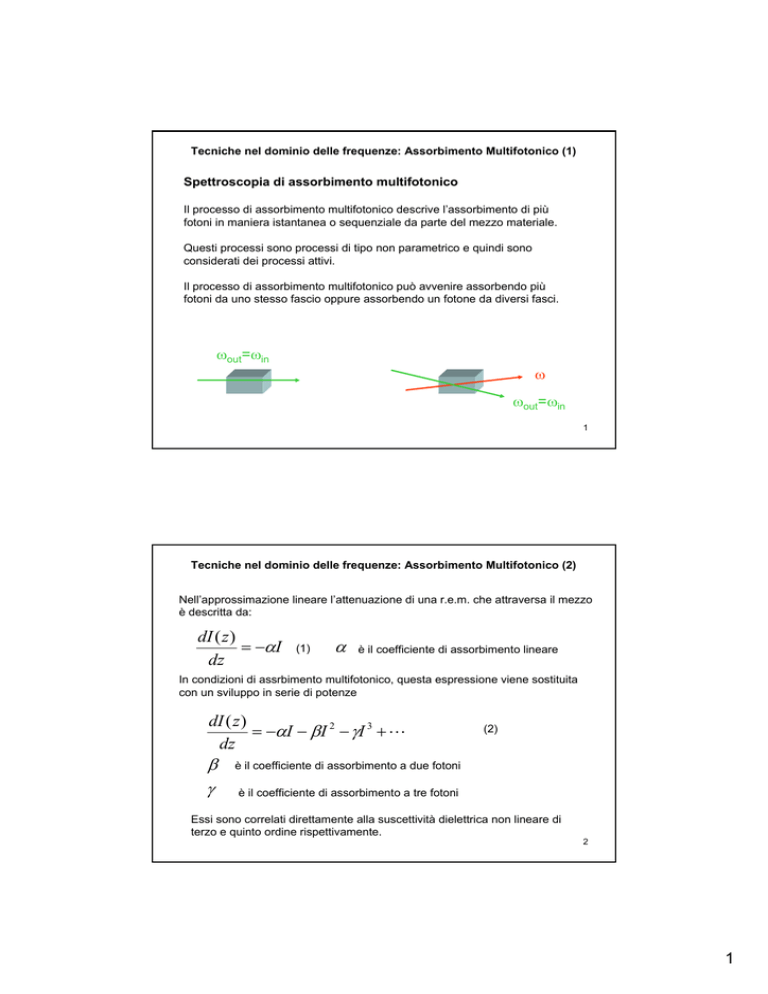
Il processo di assorbimento multifotonico può avvenire assorbendo più
fotoni da uno stesso fascio oppure assorbendo un fotone da diversi fasci.
ωout=ωin
ω
ωout=ωin
1
Tecniche nel dominio delle frequenze: Assorbimento Multifotonico (2)
Nell’approssimazione lineare l’attenuazione di una r.e.m. che attraversa il mezzo
è descritta da:
dI ( z )
= −αI
dz
(1)
α
è il coefficiente di assorbimento lineare
In condizioni di assrbimento multifotonico, questa espressione viene sostituita
con un sviluppo in serie di potenze
dI ( z )
= −αI − β I 2 − γI 3 + L
dz
β
γ
(2)
è il coefficiente di assorbimento a due fotoni
è il coefficiente di assorbimento a tre fotoni
Essi sono correlati direttamente alla suscettività dielettrica non lineare di
terzo e quinto ordine rispettivamente.
2
1
Assorbimento a due fotoni: TPA (1)
Focalizziamo l’attenzione sul processo TPA: Two Photon Absorption
Consideriamo il caso in cui si ha l’attenuazione di un solo fascio
ωout=ωin
Nel risolvere l’equazione di Maxwell relativa al campo elettrico che viene
attenuato, dobbiamo inserire come termine sorgente una polarizzazione non
lineare che oscilla alla stessa frequenza del campo applicato. Se ci limitiamo a
considerare il primo termine e non-lineare: ovvero il termine al terzo ordine la
allora la polarizzazione non lineare sarà data dalla combinazione di frequenze:
ω = ω +ω −ω
(3)
Poiché si tratta di un processo attivo, non parametrico l’attenuazione del
segnale sarà proporzionale alla parte immaginaria della polarizzazione non
lineare.
3
Assorbimento a due fotoni: TPA (2)
dI (ω , z )
4πω
= −I
Im[P(ω , z ) E (ω , z )]
dz
cn
(4)
P(ω , z ) = χ ( 3) (ω , ω ,−ω , ω ) E (ω , z )E * (ω , z )E (ω , z )
(5)
Sostituendo la (5) nella (4) si ha:
dI (ω , z )
16π 2ω
= − I 2 2 2 Im χ ( 3) (ω , ω ,−ω , ω )
dz
c n
[
]
(6)
Confrontandola con l’espressione (2) si ha:
β=
16π 2ω
Im χ ( 3) (ω , ω ,−ω , ω )
2 2
c n
[
]
c è la velocità della luce e n l’indice di rifrazione
(7)
4
2
Assorbimento a due fotoni: TPA (3)
Definiamo ora il valore medio della sezione d’urto TPA per una singola molecola
attiva presente nel materiale e per singolo fotone:
σ TPA =
hωβ 16π 2ω 2 h
= 2 2
Im χ ( 3) (ω , ω ,−ω , ω )
N
c n N
[
]
(9)
N è il numero di molecole per unità di volume. E le parentesi <> indicano
media orientazionale
In letteratura in genere si trova la seguente formula:
hωβ 8π 2ω 2 h 4
= 2 2 L Im γ (3) (ω , ω ,−ω , ω )
N
c n
χ ( 3) (ω , ω ,−ω , ω )
γ (3) (ω , ω ,−ω , ω ) =
N
γ(3) viene definita iperpolarizzabilità molecolare. L è il fattore di campo
[
σ TPA =
]
(10)
(11)
locale e rende conto del campo effettivo che influenza la molecola nel
mezzo materiale ed il fattore 8 dipende da come è stato definito il campo
elettrico
5
Assorbimento a due fotoni: TPA (4)
Il processo di assorbimento a due fotoni può aver luogo attraverso due
modalità: processo istantaneo e processo sequenziale:
istantaneo
Impulsi laser corti
(~100 fs)
sequenziale
Impulsi laser lunghi
(~10 ns)
6
3
Assorbimento a due fotoni: TPA (5)
Istantaneo
¾ Emissione laser indotta da TPA
¾ Fofto-polimerizzazione indotta da TPA
¾ Fluorescenza indotta da TPA per imaging di materiali e
sistemi biologici
Sequenziale
¾ Limitazione ottica di r.e.m. intense
¾ Terapia fotodinamica indotta da TPA
7
Assorbimento a due fotoni: TPA (6)
Nel seguito centriamo l’attenzione sui processi istantanei, ovvero i
processi in cui due fotoni di energia confrontabile con la metà dell’energia
di transizione delle molecole esaminate, vengono assorbiti
contemporaneamente dalla molecola.
Le molecole che risultano avere una sezione d’urto TPA di notevole
ampiezza sono molecole che presentano gruppi elettron-attrattori (A) e
gruppi elettron-donatori (D) collegati attraverso ponti π coniugati che
permettono una efficiente delocalizzazione della carica elettronica.
Tra queste molecole ci sono composti:
Dipolari
Quadrupolari
Ottupolari
D-π-A
D-π-A-π-D
A-π-D-π-A
D-π-D
A-π-A
D
π
π
D
A
π
D
8
4
Assorbimento a due fotoni: TPA (7)
Descrizione della iperpolarizzabilità molecolare per un semplice sistema a
due livelli: adatto per descrivere molecole di tipo push-pull D-π-A.
e
g
Dei 48 termini che compongono la suscettività dielettrica non lineare solo 24
sono indipendenti, dal momento che due frequenze sono identiche, inoltre
trascuriamo tutti i termini che non danno risonanza a due fotoni e tra questi
manteniamo solo quelli che non presentino antirisonanze:
rimangono solo due termini i cui diagrammi sono:
1.
e
ω
−ω
2.
e
ω
i,j
ω
ωeg + ω. In tutto
i,j
ω
−ω
g
g
9
Assorbimento a due fotoni: TPA (8)
Utilizzando la tecnica diagrammatica si ha:
γ 1(.3) =
µ gi µie µ ej µ jg ρ gg
1
3 ∑
h i , j =e, g (ωig − ω − iΓig )(ωeg − 2ω − iΓeg )(ω jg − ω − iΓ jg )
γ 2(3. ) =
µ gi µie µ ej µ jg ρ gg
1
3 ∑
h i , j =e, g (ωig − ω − iΓig )(ωeg − 2ω − iΓeg )(ωej − ω − iΓej )
(12)
(13)
Sostituendo i e j con e e g si ottengono 4 termini nella somma, se si fanno le
seguenti approssimazioni:
Γij << ωij
Γii << ω
Γeg << ωeg − ω
ωeg − ω ≈ ω
10
5
Assorbimento a due fotoni: TPA (9)
µ ge (µ ee − µ gg ) ρ gg
2
= 3
h (ωeg − ω )2 (ωeg − 2ω − iΓeg )
2
γ
( 3)
=γ
( 3)
1.
+γ
( 3)
2.
2
0
(14)
Quindi la parte immaginaria da cui dipende la sezione d’urto TPA risulta:
σ TPA ∝ Im[γ
( 3)
]
µ ge (µ ee − µ gg ) ρ gg Γeg
2
= 3
h (ωeg − ω )2 (ωeg − 2ω )2 − Γeg2
2
0
[
]
(15)
Maggiore è il momento di dipolo di transizione e maggiore è la variazione
tra il momento di dipolo di stato fondamentale e stato eccitato, maggiore
sarà la sezione d’urto di assorbimento a due fotoni. Per questo motivo
molecole polari come quelle precedentemente descritte risultano avere la
risposta non lineare più intensa.
11
Assorbimento a due fotoni: TPA (10)
Per descrivere i due stati g ed e nel sistema dipolare: D-π-A si parte da due
configurazioni limite:
D+ -π- A¯
D-π-A
CT
N
Si suppone che queste due forme limite si trovino a distanza di energia pari
a V e che l’interazione tra le due, che permette il trasferimento di carica, si
uguale a -t
V = CT Hˆ CT − N Hˆ N
t = − CT Hˆ N
(16)
(17)
tan ϑ =
2t
V
(18)
Risolvendo l’hamiltoniano si ottengono i due stati:
g = cos(ϑ 2) N + sin (ϑ 2) CT
(19.a)
e = − sin (ϑ 2 ) N + cos(ϑ 2 ) CT
(19.b)
Barzoukas et al., J. Chem. Phys., 113, (2000), 3951
12
6
Assorbimento a due fotoni: TPA (11)
e
CT
V
V + V 2 + 4t 2
2
V 2 + 4t 2
N
g
V − V 2 + 4t 2
2
Definiamo il parametro MIX che descrive il grado di mescolamento delle due
forme nei vari stati:
V
ϑ
ϑ⎞
⎛
MIX = −⎜ cos 2 − sin 2 ⎟ = − cos ϑ = −
2
2
2⎠
⎝
V + 4t 2
(20)
Barzoukas et al., J. Chem. Phys., 113, (2000), 3951
13
Assorbimento a due fotoni: TPA (12)
MIX = 1 cos ϑ = −1 ϑ = π
MIX = 0 cos ϑ = 0 ϑ = π 2
MIX = −1 cos ϑ = 1 ϑ = 0
g = CT
e = N
g = e =1
g = N
2 CT + 1
e = CT
2N
(21)
Barzoukas et al., J. Chem. Phys., 113, (2000), 3951
14
7
Assorbimento a due fotoni: TPA (13)
E’ possibile descrivere la suscettività dielettrica al secondo ordine in funzione
del parametro MIX, dal momento che:
V
MIX
µ + µCT + µCS ⋅ MIX
µ gg = N
2
µ + µCT − µCS ⋅ MIX
µ ee = N
2
µ ⋅ 1 − MIX
µ eg = CS
2
µCS = µCT − µ N
hωeg = −
Dove:
µ N e µCT
Sono i momenti di configurazioni
limite.
(22)
Se sostituiamo queste espressioni nell’equazione (15) ,
consideriamo di trovarci sul massimo della risonanza a due fotoni (ωeg
e poniamo uguale a 1 la popolazione iniziale nello stato g, allora:
= 2 ω)
15
Assorbimento a due fotoni: TPA (14)
σ TPA ∝
4
µCS
16t 2
(1 − MIX )2 MIX 2
La sezione d’urto raggiunge il suo
massimo valore quando
MIX=±1/√3. Ovvero quando lo
stato fondamentale ed ecitato
sono una giusta mescolanza
delle due forme limite
Inoltre essa risulta tanto
maggiore quanto più forte è la
coppia D/A, e quindi µCS e
qunato più lunga sarà la distanza
tra D e A purchè il trsferimento di
carica non perda in efficienza.
Barzoukas et al., J. Chem. Phys., 113, (2000), 3951
16
8
Assorbimento a due fotoni: TPA (15)
Modelli simili sono stati sviluppati anche per sistemi quadrupolari ed ottupolari.
Inoltre nei modelli sono stati inseriti anche accoppiamenti con modi vibrazionali
propri della molecola come pure interazioni con il solvente che viene descritto
come un mezzo continuo caratterizzato dalla sola costante dielettrica.
Vedi M. Cho , A Painelli
Contemporanemente sono stati approntati calcoli computazionali che permettono
di ottenere i valori dei parametri che entrano nell’espressione della
iperpolarizzabilità in maniera più accurata, senza far ricorso a qeusto tipo di
odellini semplici, ma estendendo la somma anche a stati diversi dal primo livello
eccitato.
Vedi A. Agren, e S. Tretiak.
17
Assorbimento a due fotoni: TPA (16)
Metodi di misura del coefficiente di assorbimento TPA
• Tecnica di Z-scan in condizioni open aperture
• Tecnica di IR Pump- White Light Continuum Probe Spectroscopy
• Tecnica di Fluorescenza indotta da TPA
18
9
Assorbimento a due fotoni: TPA (17)
Esperimenti di Z-scan Open aperture
F
Sample
z0
L
Z
D
PD
L
TN
dI
= −(α + β I ) I
dz
1
M. Sheik-Bahae, E.W. Van Stryland, et al, IEEE
J. of Quantum Electronics 26, (1990), 760.
z0
Z
19
Assorbimento a due fotoni: TPA (18)
Integrando l’equazione differenziale, nell’ ipotesi che l’assorbimento sia piccolo,
si ottiene la trasmittanza normalizzata del fascio
β I 0 Leff
I ( z)
= 1−
I (− ∞ )
1 + ( z − z0 ) 2 z w2
TN =
βI 0 Leff < 1
Dove:
Leff =
zw =
I0 =
1 − exp(− α L )
π w02
λ
Lz == spessore del campione della direzione
w
di propagazione del fascio
α
Rayleigh Range: permette di determinare w0 il diametro
del fascio sul fuoco
π 3 / 2 w02 E ( J )σ τ
2 ln 2
E (J ) Energia dell’impulso
στ
Controllare con Elisabetta
Durata dell’impulso
20
10
Assorbimento a due fotoni: TPA (19)
β
E’ una proprietà macroscopica del materiale che ha come unità di
misura cm/GW
Se si conosce la densità di molecole attive nel materiale e la loro disposizione,
è possibile calcolare la sezione d’urto TPA efficace per ogni singola molecola
σ TPA =
βhω
N
Che ha come unità di misura:
cm4 s photon-1 molecule-1
Si definisce come unità di misura
GM = Göppert Mayer (dalla sceinziata che per prima
Ipotizzò uesto processo negli anni ’30)
1 GM = 10-50 cm4 s photon-1 molecule-1
Per ottenere lo spettro TPA bisogna ripetere l’esperimento di Z-scan per ogni
lunghezza d’onda di interesse.
21
Assorbimento a due fotoni: TPA (20)
IR Pump-White Light Continuum Probe (IRP-WLPC)
τpulse = 150 fs
Il fascio in uscita dal laser viene separato in
due fasci (entrambi non risonanti ad un
fotone):
pump
probe
detector
sample
Pump (90%) che mantiene la λ del laser fissa
λpump = 812 nm
Probe(10%): il fascio laser focalizzato sua
una finestra di zaffiro generando una luce
bianca impulsata ce si estende in tutto
l’intervallo del visibile
λprobe = 450 - 1100 nm
R.A.Negres, E.W. Van Stryland, E.W. IEEE
J. of Quantum Electronics 38, (2002), 1205.
22
11
Assorbimento a due fotoni: TPA (21)
Quando il probe arriva
normalized transmittance
I due impulsi vengono incrociati spazialmente sul campione e misura
l’attenuazione del probe in funzione del ritardo temporale tra l’appplicazione
del pump e del probe
Prima del pump:
non subisce attenuazione non lineare
perché è troppo poco intenso
Contemporaneamente al pump:
Assorbimento a due fotoni: uno dal
pump ed uno dal probe
1,0
0,9
0,8
-2
Dopo il pump:
non subisce attenuazione non lineare
perché è troppo poco intenso
-1
0
1
2
delay time (ps)
23
Assorbimento a due fotoni: TPA (22)
L’attenuazione del probe in presenza del pump viene descritta, in forma
differenziale da:
dI probe
dz
T probe =
= − β ' I probe I pump
I probe (t = 0)
I probe (t = −∞ )
= 1 − β '⋅I pump ⋅ k
t = ritardo temporale tra pump e probe
k = costante che dipende dalle caratteristiche geometriche dell’esperimento
N.B
IRP-WLCP
Z-scan
β ' (ω probe , ω pump ,−ω pump , ω probe ) ≠ β (ω pump , ω pump ,−ω pump , ω pump )
I dati vengono normalizzati usando la misura di Z-scan nell’unico
punto in cui ωpump = ωprobe
24
12
Assorbimento a due fotoni: TPA (23)
Two Photon induced Fluorescence (TPF)
pump
detector
sample
Utilizzabile solo se le
molecole sono fluorescenti
filter/
momochrom.
Il fascio laser viene focalizzato sul campione e si raccoglie la fluorescenza che
Viene emessa a 90°. Si utilizzano dei filtri o un monocromatore per separare la
fluorescenza dalla luce laser eccitatarice.
Caratteristiche del laser :
λ = 700 - 1000 nm τpulse = 150 fs
C. Xu, W.W. Webb, J.Opt. Soc. Am. B, 13, 1996, 481
25
Assorbimento a due fotoni: TPA (24)
Con questo set-up si possono effettuare due tipi di misure:
TPF Emission : Misura dello spettro di fluorescenza eccitato da TPA:
Si misura la dispesione spettrale della fluorescenza eccitando ad una
certa lunghezza d’onda fissa. Da questa misura si può vedere se lo
stato che emette è lo stesso sia che il sistema venga eccitato ad uno
che a due fotoni.
TPF Excitation : Misura dello spettro di eccitazione di fluorescenza
dovuto a TPA. Si raccoglie tutta la fluorescenza emessa e la si misura
in funzione della lunghezza d’onda di eccitazione usata , cioè variando
la lunghezza d’onda del laser incidente. Da questa misura è possibile
ricavare lo spettro a due fotoni.
26
13
Assorbimento a due fotoni: TPA (25)
TPE- Emission:
Spettro di emissione della fluoresceina in acqua a pH basico eccitata a 488 nm
(un fotone) linea continua ed a due fotoni (900 nm) linea tratteggiata.
C. Xu, W.W. Webb,
J.Opt. Soc. Am. B,
13, 1996, 481
27
Assorbimento a due fotoni: TPA (26)
TPF Excitation
λecc. = 800 nm
5
Emissione (A.U.)
Per ogni lunghezza d’onda di
eccitazione si misura l’intensità del
segnale di fluorescenza in
funzione dell’inetnsitò del laser
incidente.
Se il processo è TPA si deve
osservare un andamento
quadratico.
6
2
Emiss. = P1 I
4
3
2
1
0
0
1
F (t ) = η 2σ TPAΦCV I 2 (t )
2
1
2
3
Intensità incidente (A.U.)
4
F = Segnale di fluorescenza
η2 = quantum yield di fluorescenza
Φ= funzione responso strumentale
V = volume attivo
C = concentrazione di molecole attive
C. Xu et al., J. Opt. Soc. Am. B, 1996, 13, 481
28
14
Assorbimento a due fotoni: TPA (27)
Poiché non è facile valutare la funzione responso strumentale, dopo le prime
misure di Xu e Webb, si sono utilizzati i loro dati come riferimento per
standardizzare le altre misure, in questo la sezione d’urto di assorbimento a due
fotoni viene ricavata dalla relazione
P1S nS2ηR CR R
σ =
σTPA
P1R nR2 ηS CS
S
TPA
S = campione incognito, R = riferimento
n = indice di rifrazione
P1i= coefficienti della funzione quadratica usata per effettuare il fit dei dati di
intensità del segnale di fluorescenza in funzione dell’intensità laser incidente.
I riferimenti più usati sono al momento
La fluoresceina in acqua a pH > 10
Derivati del bistirilbenzene in toluene.
29
Assorbimento a due fotoni: TPA (28)
Applicazioni della tecnica TPA
1. Caratterizzazione delle proprietà di composti: dipolari, quadrupolari e
ottupolari
2. Emissione stimolata indotta da TPA
3. Fotopolimerizzazione indotta da assorbimento a due fotoni
4. Generazione di ossigeno di singoletto
5. Tecniche di imaging a livello microsocopico in campo bio-medico
6. Confronto con la tecnica SHG
30
15
Assorbimento a due fotoni: TPA (29)
1. Esempio 1: composti: dipolari, quadrupolari e ottupolari
31
Assorbimento a due fotoni: TPA (30)
Sistema modello che descrive gli stati eccitati CT del sistema (uno per ogni
ramo) e suppone che ci sia un interazione di tipo eccitonico (V) tra essi.
N.B.
Nel sistema D-A lo stato eccitato è accessibile a uno e due fotoni
Nel sistema a V (quasi-quadrupolare) entrambe i livelli eccitati sono
permessi sia ad uno che a due fotoni,
Nel sistema ottupolare i primi due stati degeneri sono accessibili ad uno e
due fotoni, mentre lo stato eccitato di maggiore solo a due fotoni.
32
16
Assorbimento a due fotoni: TPA (31)
Spettri ad un fotone ~ 1x10-6 M
Spettro di emissione
Spettro di assorbimento
Mentre nell’assorbimento si nota lo spostamento del massimo di minore
energia, come previsto dal modello, nella fluorescenza gli spettri
coincidono. Indice del fatto che , dopo l’eccitazione iniziale delocalizzata
si ha una localizzazione (intrappolamento) dell’eccitazione su uno dei
rami che quindi emette.
33
Assorbimento a due fotoni: TPA (32)
TPA Set-Up sperimentale
700-1000 nm, 80 fs 80 MHz
34
17
Assorbimento a due fotoni: TPA (33)
Spettri TPA
Si nota un aumento dell’intensità di TPA
Andando dal dipolare all’ ottupolare come
pure una distribuzione di intensità molto
diversa.
Ad es nel V-shaped le due transizioni
hanno intensità opposta nei due casi.
C ~ 1x10-4 M
35
Assorbimento a due fotoni: TPA (34)
Effetti di amplificazione cooperativa del segnale:
Mentre attorno a 800 nm non si
osserva una netta amplificazione del
segnale, si ha invece una
amplificazione sia al di sopra degli
850 nm che al di sotto dei 750 nm.
36
18
Assorbimento a due fotoni: TPA (35)
1. Esempio 2: aggregati di porfirine
Spettro di assorbimento lineare
(2E -6)
(4E -6)
(8E -6)
(5E -5)
(8E -5)
(2E -4)
(4E -4)
(8E -4)
ε
400000
M
M
M
M
M
M
M
M
200000
0
400
600
Lunghezza d'onda (nm )
O. Ohno, Y. Kaizu, and H. Kobayashi,
J. Chem. Phys. 99, (1993), 4128
37
Assorbimento a due fotoni: TPA (36)
Z-scan of H4TPPS2- misurato @ 810 nm con impulsi : τ = 150 fs
I0 = 1.67x1011 W/cm2, w0 = 20 ± 5 µm
• aggragto in acqua a pH<1 C = 1x10-3 M
• monomero in acqua/DMSO/urea C = 1x10-2 M
σTPA (GM)
Normalized Transmittance
1,0
aggregato
1000±200
monomero
30*±15
0,9
0,8
0,7
-20
0
Z (mm)
20
* In agreement with data
by M. Drobizhev et al.,
Chem.Phys.Lett., 355,
(2992), 175
E. Collini, et al , J. Phys. Chem. B, 109, (2005), 2
38
19
Assorbimento a due fotoni: TPA (37)
Influenza dell’irradianza del fascio incidente su σTPA
60
λexc = 810 nm
τpulse = 150 fs
σTPA (GM)
1200
40
Aggregato in acqua
C = 1x10-3 M
800
20
400
0
2
0
4
monomero in
acqua /DMSO/urea
C = 1x10-2 M
0
2
11
4
2
I0 (10 W/cm )
Mentre l’aggreagto mostra un aumento della σTPA all’aumentare
dell’irradianza, il monomero pare rimanere costante (problemi di
S/N)
39
Assorbimento a due fotoni: TPA (38)
Spettro TPA misurato con IR Pump-WLPC technique
aggregato in acqua
C = 1x10-3 M
12
TPA
150
σ
8
0
380
3
σTPA (10 GM)
(G M )
300
400
42 0
monomero in
acqua/DMSO/urea
C = 1x10-2 M
λ (n m )
4
0
380
400
420
440
Dati normalizzati
rispetto alla misura di Zscan effettuata a 810
nm.
λpump+probe (nm)
λ pump + probe =
λ pump ⋅ λ probe
λ pump + λ probe
E. Collini, et al J. Phys. Chem. B,
109, (2005), 2
40
20
Assorbimento a due fotoni: TPA (39)
Conclusioni:
• Si osserva una netta amplificazione del responso non lineare in tutto l’intervallo
di lunghezze d’onda indagato passando dal monomero diacido all’aggregato
che noi attribuiamo ad effetti coopertivi: ovvero alla presenza degli stati
eccitonici.
• Osserviamo una spalla a 410 nm nello spettro dell’aggregato che non sembra
essere presente in quello del monomero. Questa spalla può essere dovuta a.
• Formazione di un dimero CT tra due unità di porfirina adiacenti
• Transizione permessa a due fotoni del monomero di bassa
intensità, che viene amplificata per interazione con lo stato
due-eccitonico della banda Q dell’aggregato
41
Assorbimento a due fotoni: TPA (40)
2. Esempio 3: Emissione laser indotta da TPA
Polimero HEMA contenente dei gruppi D-π-A dotati di buona fluorescenza e
buon TPA
In HEMA
(2-hydroxyethylmethacrilate)
polymer
C=2x10-2M
Laser Output: 1064 nm, 50 ps, 10Hz
Rivelatore: Streak Camera 2 ps risoluzione temporale
Le pareti del polimero funzionano da specchi di fine cavità
D. Wang et al, Chem. Phys. Lett., 354, (2002), 423
42
21
Assorbimento a due fotoni: TPA (41)
λexc = 1064 nm , τpulse= 50 ps
pulse
ASE
laser
Caratteristiche di emissione in
funzione della lunghezza d’onda
Caratteristiche di emissione in
funzione del tempo
D. Wang et al, Chem. Phys. Lett., 354, (2002), 423
43
Assorbimento a due fotoni: TPA (42)
2. Esempio 4: Emissione laser indotta da TPA
H3C
522 nm
1,2
532 nm
0,6
reference
H3C
555 nm
0,4
0,2
0,0
480
CH3
N
N
CF3SO3
0,8
790 nm
N
H3C
1,0
150 fs
N
CF3SO3
557 nm
500
520
540
nm
560
580
H3C
H3C
CH3
N
CH3
N
CF3SO3
600
CH3
N
CH3
N
CF3SO3
576 nm
N
CF3SO3
CH3
N
Soluzioni dei coloranti in DMSO C ~ 2x10-2 M.
Pompate con un laser a Ti-zaffiro a 790nm,
Le pareti della cuvetta agiscono da specchi di fine cavità
Adv. Mater. 2000, 12, 1963 (review); Synth. Met. 2001, 121, 1755
44
22
Assorbimento a due fotoni: TPA (43)
3. Esempio 5: Fotopolimerizzazione TPA
The TPA process promotes
a photopolimerization
process, by a two-photon
excitation of the
polimerization initiator
Sub-micrometric resolution,
thanks to the higher spatial
discrimination of the TPA
process (I2 dependence)
Scale bar = 200 nm, λexc = 780 nm , τpulse= 150 fs, Epulse = 120 pJ
S. Kawata et al., Nature, 412, (2001), 697
45
Assorbimento a due fotoni: TPA (44)
The TPA process promotes
a photopolimerization
process, by a two-photon
excitation of the
polimerization initiator
Sub-micrometric resolution,
thanks to the higher spatial
discrimination of the TPA
process (I2 dependence)
Scale bar = 200 nm, λexc = 780 nm , τpulse= 150 fs, Epulse = 120 pJ
46
23