(t) + - Università degli Studi di Roma "Tor Vergata"

M. Salerno
Tor Vergata
Laplace
1
Interruttore ideale
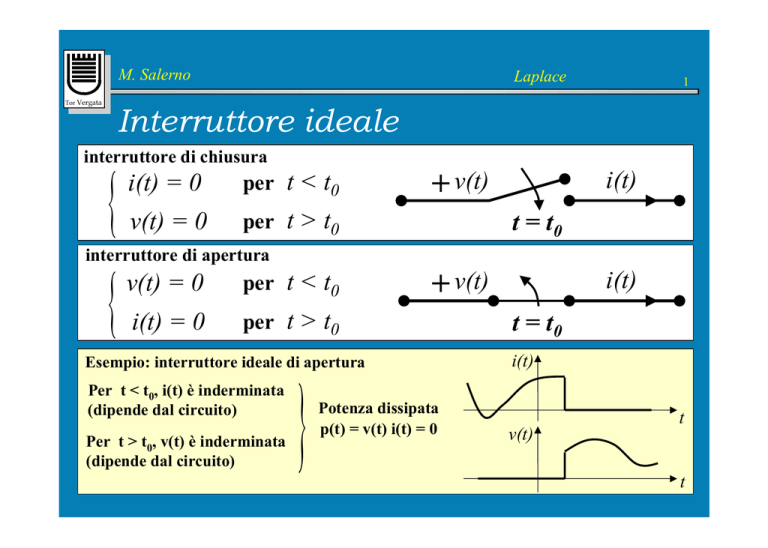
interruttore di chiusura
{
{
i(t) = 0
per t < t0
v(t) = 0
per t > t0
+ v(t)
i(t)
t = t0
interruttore di apertura
v(t) = 0
per t < t0
i(t) = 0
per t > t0
}
+ v(t)
Esempio: interruttore ideale di apertura
Per t < t0, i(t) è inderminata
(dipende dal circuito)
Per t > t0, v(t) è inderminata
(dipende dal circuito)
Potenza dissipata
p(t) = v(t) i(t) = 0
i(t)
t = t0
i(t)
v(t)
t
t
M. Salerno
Tor Vergata
Laplace
1
Interruttore ideale
interruttore di chiusura
{
{
i(t) = 0
per t < t0
v(t) = 0
per t > t0
+ v(t)
i(t)
t = t0
interruttore di apertura
v(t) = 0
per t < t0
i(t) = 0
per t > t0
}
+ v(t)
Esempio:
interruttore ideale di apertura
Caso
reale
Nell’intervallo
(intervallo di apertura), v(t) , i(t) e
Per t < t0, i(t) èδinderminata
la
potenzadal
dissipata
p(t) sono diverse
da zero.
Potenza
dissipata
(dipende
circuito)
p(t)
Gli interruttori sono caratterizzati
da:= v(t) i(t) = 0
Per t > t0, v(t) è inderminata
l’intervallo δ (interruttori rapidi, extrarapidi, ecc.)
(dipende dal circuito)
la massima corrente e la massima tensione
i(t)
t = t0
i(t)
v(t)
δ
t
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
vC (t)
Per t < 0
+
vR (t)
Il circuito è formato da tre componenti
il condensatore C
il resistore R
l’interruttore, che si chiude per t = 0
R
Si supponga che vC(t) = V0 , per t < 0
V0 condizione iniziale
Per t > 0 , interruttore chiuso : vC (t) = vR(t)
Determinazione equazione risolvente
i(t) = 0
vC(t) = V0
vR(t) = 0
i(t) = - C d vC (t) / dt = - C d vR(t) / dt = - C d R i(t) / dt
Attenzione
ai segni coordinati
sul condensatore
RC di(t) / dt + i(t) = 0
Equazione risolvente
2
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
vC (t)
+
vR (t)
Il circuito è formato da tre componenti
il condensatore C
il resistore R
l’interruttore, che si chiude per t = 0
R
Si supponga che vC(t) = V0 , per t < 0
V0 condizione iniziale
Per t < 0
Per t > 0 , interruttore chiuso : vC (t) = vR(t)
i(t) = 0
Determinazione
equazione
risolvente
Risoluzione
equazione
risolvente
RC di(t) / dt + i(t) = 0
t +d A
α t /=dt0
i(t)scelga
= - C di(t)v =(t)A/edtα t= - C d v RC
(t) / Adtα =e -α C
R ei(t)
Si
vC(t) = V0
vR(t) = 0
C
R
Equazione
caratteristica
RC α + 1 = 0
Attenzione
RC di(t) / dt + i(t) = 0
ai segni coordinati
α = - 1 / RC
i(t) = A e − t / RC
sul condensatore
Equazione risolvente
Integrale generale
2
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
2
vC (t)
+
vR (t)
R
Sicircuito
definiscono
gli istanti
Il
è formato
da tre componenti
til=condensatore
0 (lim per t C→ 0 da sinistra)
R t → 0 da destra)
til=resistore
0+ (lim per
l’interruttore,
che sidiscontinuità
chiude per t =di0
Non
essendo possibili
tensione
sul condensatore
Si supponga
che vC(t) = V0 , per t < 0
V condizione
v (0+) =iniziale
v (0-) = V
0
C
C
0
; i(t) = A e − t / RC
Per t < 0
Per t > 0 , interruttore chiuso : vC (t) = vR(t)
i(t) = 0
Calcolo dell’integrale
particolare
Determinazione
equazione
risolvente
Risoluzione
equazione
risolvente
RC di(t) / dt + i(t) = 0
+) = A e − t / RC α t= A = v (0+) / R = Vα t/ R
α t /=dt0
i(0scelga
i(t)
= - C di(t)v =(t)A/edt - C d v RC
(t) / Adtα =e - C+d AR ei(t)
Si
vC(t) = V0
vR(t) = 0
C
|t=0
CR
0
Equazione
caratteristica
RC
α + 1 particolare
=0
Attenzione
l’integrale
è
−
t
/
RC
RC
di(t)
/
dt
+
i(t)
=
0
i(t)
=
(V
/
R)
e
ai segni coordinati
− t / RC
stato
la
α0 = - 1 / RC
i(t)calcolato
= A e utilizzando
sul
condensatore
integrale
particolare
Equazione
risolvente
condizione
iniziale
Integrale generale
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
vC (t)
+
vR (t)
R
t<0
i(t) = 0 , vC (t) = V0 , vR(t) = 0
t>0
i(t) = (V0 / R) e − t / RC
vC (t) = vR (t) = V0 e − t / RC
τ = RC
costante di tempo
3
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
t<0
i(t) = 0 , vC (t) = V0 , vR(t) = 0
t>0
τ
i(t) = (V0 / R) ee −− tt/ /RC
τ
vC (t) = vR (t) = V0 ee −−tt/ /RC
τ = RC
costante di tempo
costante di tempo τ in secondi ( s )
Dal valore di τ dipende la velocità
di decadimento della tensione e
della corrente
vC (t)
V0
R = 10 MΩ, C = 1 mF, τ = 104 s
(più di 2 ore e 45 minuti)
R = 10 Ω, C = 10 pF, τ = 10-10 s
= 100 ps
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
t<0
i(t) = 0 , vC (t) = V0 , vR(t) = 0
t>0
τ
i(t) = (V0 / R) ee −− tt/ /RC
τ
vC (t) = vR (t) = V0 ee −−tt/ /RC
τ = RC
costante di tempo
costante di tempo τ in secondi ( s )
Dal valore di τ dipende la velocità
di decadimento della tensione e
della corrente
grandi valori di τ
vC (t)
V0 V
0
R = 10 MΩ, C = 1 mF, τ = 104 s
(più di 2 ore e 45 minuti)
R = 10 Ω, C = 10 pF, τ = 10-10 s
= 100 ps
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
t<0
i(t) = 0 , vC (t) = V0 , vR(t) = 0
t>0
τ
i(t) = (V0 / R) ee −− tt/ /RC
τ
vC (t) = vR (t) = V0 ee −−tt/ /RC
τ = RC
costante di tempo
costante di tempo τ in secondi ( s )
Dal valore di τ dipende la velocità
di decadimento della tensione e
della corrente
grandivalori
valorididiττ
piccoli
vC (t)
V0 V
0
R = 10 MΩ, C = 1 mF, τ = 104 s
(più di 2 ore e 45 minuti)
R = 10 Ω, C = 10 pF, τ = 10-10 s
= 100 ps
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
t<0
i(t) = 0 , vC (t) = V0 , vR(t) = 0
t>0
τ
i(t) = (V0 / R) ee −− tt/ /RC
τ
vC (t) = vR (t) = V0 ee −−tt/ /RC
τ = RC
costante di tempo
costante di tempo τ in secondi ( s )
Dal valore di τ dipende la velocità
di decadimento della tensione e
della corrente
grandivalori
valorididiττ
piccoli
vRC (t)
V0 V
0
R = 10 MΩ, C = 1 mF, τ = 104 s
(più di 2 ore e 45 minuti)
R = 10 Ω, C = 10 pF, τ = 10-10 s
= 100 ps
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
t<0
i(t) = 0 , vC (t) = V0 , vR(t) = 0
t>0
τ
i(t) = (V0 / R) ee −− tt/ /RC
τ
vC (t) = vR (t) = V0 ee −−tt/ /RC
τ = RC
costante di tempo
costante di tempo τ in secondi ( s )
Dal valore di τ dipende la velocità
di decadimento della tensione e
della corrente
R = 10 MΩ, C = 1 mF, τ = 104 s
(più di 2 ore e 45 minuti)
R = 10 Ω, C = 10 pF, τ = 10-10 s
= 100 ps
|
i(t)piccoli
=
(V0 / R)
e − t / RC
grandi
valori
valori
diditτ>τ0
iv(t)
C (t)
R
V0 V
0
V0 /R
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
Conservazione
t<0
i(t) dell’energia
= 0 , vC (t) = V0 , vR(t) = 0
Per t < 0, l’energia EC immagazzinata
t/ /RC
τ
t > 0dal condensatore
i(t) = (V0 /èR)
ECee=−− t½
C V02
τdal
Per t > 0,
vC l’energia
(t) = vR (t)E=R assorbita
V0 ee −−tt/ /RC
resistore è: ER = ½ C V02
τ = RC
costante di tempo
C =E
costante di E
tempo
τ Rin secondi ( s )
∞ di τ dipende la velocità
Dal valore
ERdecadimento
= R i2(t) dtdella tensione e
di
-∞
della corrente
∞
RC 4dt
= RC(V=0 1/RmF,
)2 e τ– 2=t / 10
R = 10 MΩ,
s
∫
∫0
(più di 2 ore e 45 minuti)
∞
t / RC
-10 ]
= [C- =½10
C pF,
V0 2τe =– 210
R = 10 Ω,
s0
= 100 ps
=½CV 2
0
|
i(t)piccoli
=
(V0 / R)
e − t / RC
grandi
valori
valori
diditτ>τ0
iv(t)
C (t)
R
V0 V
0
V0 /R
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
Determinazione
Conservazione
dell’area
Q =della
t<0
i(t) dell’energia
= 0 , vC (t)
V0 , forma
vR(t) = 0
d’onda
i(t) E immagazzinata
Perdi
t <corrente
0, l’energia
C
t/ /RC
τ
indipendente
t > 0dal
i(t)==C(V
Si ha
Q
V00 /èR)
condensatore
ECee=−− t½
C V02da R
τdal
Q è Per
la quantità
diEcarica
−−tt/ /RC
t > 0,
vC l’energia
(t)totale
= vR (t)
=R assorbita
V0 eeelettrica
che resistore
transita nel
per
è: circuito
ER = ½ C
V0t2> 0
τ = RC
costante di tempo
C =E
costante di E
tempo
τ Rin secondi ( s )
∞∞ di τ dipende la velocità
Dal valore
ERdecadimento
Q
== i(t)
R i2dt
(t) dtdella tensione e
di
0- ∞ ∞
della corrente
= ∞
(V0 /R ) e2 – t –/ RC
dt
2
t
/
RC 4dt
= R0C(V=0 1/RmF,
) e τ = 10
R = 10 MΩ,
s
∫∫
∫∫0
∞
(più di 2 ore
45 minuti)
– t e/ RC
= [ - C V0 e2
]RC0 ∞
–
2
t
/
= [C- =½10
C pF,
V0 τe = 10-10 ]s
R = 10 Ω,
0
= C V0
= 100 ps
= ½ C V0 2
|
i(t)piccoli
=
(V0 / R)
e − t / RC
grandi
valori
valori
diditτ>τ0
iv(t)
C (t)
R
V0 V
0
V0 /R
Q
τ
t
M. Salerno
Tor Vergata
Laplace
Scarica del condensatore
i(t)
t=0
+
C
3
vC (t)
+
vR (t)
R
∞∞ di τ dipende la velocità
Dal valore
ERdecadimento
Q
== i(t)
R i2dt
(t) dtdella tensione e
di
0- ∞ ∞
della corrente
= ∞
(V0 /R ) e2 – t –/ RC
dt
2
t
/
RC 4dt
= R0C(V=0 1/RmF,
) e τ = 10
R = 10 MΩ,
s
∫∫
∫∫0
∞
(più di 2 ore
45 minuti)
– t e/ RC
= [ - C V0 e2
]RC0 ∞
–
2
t
/
= [C- =½10
C pF,
V0 τe = 10-10 ]s
R = 10 Ω,
0
= C V0
= 100 ps
= ½ C V0 2
Determinazione
Conservazione
dell’area
Q =della
t<0
i(t) dell’energia
= 0 , vC (t)
V0 , forma
vR(t) = 0
d’onda
i(t) E immagazzinata
Perdi
t <corrente
0, l’energia
C
t/ /RC
τ
indipendente
t > 0dal
i(t)==C(V
Si ha
Q
V00 /èR)
condensatore
ECee=−− t½
C V02da R
τdal
Q è Per
la quantità
diEcarica
−−tt/ /RC
t > 0,
vC l’energia
(t)totale
= vR (t)
=R assorbita
V0 eeelettrica
che resistore
transita nel
per
è: circuito
ER = ½ C
V0t2> 0
τ = RC
costante di tempo
L’area della forma d’onda i(t) è
E
C = rispetto
costante
di E
tempo
τ Rin secondi
invariante
aR (s)
|
i(t)piccoli
=
(V0 / R)
e − t / RC
grandi
valori
valori
diditτ>τ0
iv(t)
C (t)
R
V0 V
0
al variare di R
R minore
R maggiore
V0 /R
Q
τ
t
M. Salerno
Tor Vergata
Laplace
Analisi nel dominio del tempo
Metodo di analisi di un circuito contenente interruttori:
a) determinare l’equazione differenziale risolvente
L’ordine dell’equazione differenziale risolvente è detto ordine del circuito (il
circuito RC è un circuito del primo ordine). L’ordine di un circuito non è mai
maggiore della somma del numero dei condensatori e degli induttori presenti
b) determinare l’integrale generale
L’integrale generale dipende da un numero di costanti arbitrarie pari all’ordine del
circuito
c) determinare l’integrale particolare
Le costanti arbitrarie presenti nell’espressione dell’integrale generale devono essere
calcolate in funzione delle condizioni iniziali (scelte fra le tensioni iniziali dei
condensatori e le correnti iniziali degli induttori)
4
M. Salerno
Tor Vergata
Laplace
Analisi nel dominio del tempo
Metodo di analisi di un circuito contenente interruttori:
Il metodo è detto analisi nel dominio del tempo perché
a) determinare l’equazione differenziale risolvente
tutte
ledell’equazione
grandezze
elettriche
considerate
funzioni
L’ordine
differenziale
risolvente
è detto ordinesono
del circuito
(il
circuito RC è un circuito del primo ordine). L’ordine di un circuito non è mai
del
tempo e le equazioni differenziali utilizzano il
maggiore della somma del numero dei condensatori e degli induttori presenti
tempo come l’integrale
variabile indipendente
b) determinare
generale
L’integrale generale dipende da un numero di costanti arbitrarie pari all’ordine del
circuito
presenza
di interruttori è spesso necessario
In
c) suddividere
determinarel’asse
l’integrale
particolare
dei tempi
in più tratti contigui ed
Le costanti arbitrarie presenti nell’espressione dell’integrale generale devono essere
effettuare
analisi
calcolate in funzione
delleindipendenti
condizioni iniziali (scelte fra le tensioni iniziali dei
condensatori e le correnti iniziali degli induttori)
4
M. Salerno
Tor Vergata
Laplace
Analisi nel dominio del tempo
Metodo di analisi diNel
uncaso
circuito
contenente
interruttori:
della scarica
del condensatore
è presente
t = 0 è detto analisi
IlC metodo
nel interruttore
dominioche
delsi tempo
un solo
chiude perperché
t=0
+
a) determinare
l’equazione
differenziale
risolvente
R
V
tutte
le
grandezze
elettriche
considerate
funzioni
0
L’ordine
dell’equazione differenziale
èconsiderando
detto ordinesono
deli seguenti
circuito
(il
L’analisi
è risolvente
effettuata
circuito RC è un circuito del primo
ordine).
L’ordine
un circuito non è mai
intervalli
sull’asse
deiditempi:
del
tempo e le equazioni
differenziali
utilizzano il
maggiore della somma del numero dei condensatori e degli induttori presenti
Intervallo t < 0 . In questo intervallo l’analisi è banale, essendo il circuito aperto
tempo- come l’integrale
variabile indipendente
b) determinare
generale
Intervallo 0 < t < 0 + . In questo intervallo l’analisi è banale, poiché la condizione
L’integrale generale
un numero
di costanti
arbitrarie
pari all’ordine del
inizialedipende
V0 non da
subisce
variazioni
alla chiusura
dell’interruttore
circuitot > 0 .di
Intervallo
In questo
intervallo l’analisi
è effettuata
per mezzo di una equazione
In
presenza
interruttori
è spesso
necessario
differenziale
ordinariaparticolare
del primo ordine.
c) suddividere
determinare
l’integrale
l’asse dei tempi in più tratti contigui ed
Le costanti
arbitrarielepresenti
nell’espressione
generale
devono
essere
In circuiti
più complessi
analisi per
t < 0 e per 0 - dell’integrale
< t < 0+ possono
risultare
non banali.
effettuare
analisi
indipendenti
calcolatenell’intorno
in funzione
delle
(scelte
fra le
tensionigliiniziali
dei il
L’analisi
di
t = condizioni
0 nasce daliniziali
fatto che,
quando
scattano
interruttori,
condensatori
e le correnti
iniziali degli
induttori)
circuito
si modifica
e le grandezze
elettriche
possono cambiare istantaneamente
4
M. Salerno
Tor Vergata
Laplace
5
Funzione gradino unitario
definizione
0 per t < 0
u-1(t) =
1 per t > 0
{
il gradino unitario è una funzione
discontinua utile per analizzare
circuiti contenenti interruttori,
evitando di suddividere l’asse dei
tempi in più tratti separati
la funzione u-1( t ) non è definita
per t = 0
u-1(t)
1
t
Notazione
Per il gradino unitario è usato il simbolo
u-1(t) perché questa funzione fa parte di
un insieme numerabile di enti matematici,
indicati con il simbolo uk(t) (che verranno
definiti in seguito)
In altre trattazioni sono spesso usate
notazioni differenti
M. Salerno
Tor Vergata
Laplace
5
Funzione gradino unitario
definizione
0 per t < 0
u-1(t) =
1 per t > 0
u-1(t)
{
il gradino
unitario èche
una
funzione
Schemi
equivalenti
utilizzano
discontinua
utile per analizzare
il gradino
unitario
circuiti contenenti interruttori,
generatore di tensione attivato
evitando di suddividere l’asse dei
per t = 0
tempi in più tratti separati
la funzione u-1( t ) non è definita
per t = 0
1
t
Notazione
t= 0
Per il gradino
unitario è usato il simbolo
u-1(t) perché questa
di
A funzione fa parte A
un insieme numerabile di enti matematici,
indicati con il simbolo uk(t) (che verranno
B
B
definiti in seguito)
+
+
vg(t) uusate
(t) trattazioni sono spesso
-1(t)
Invgaltre
notazioni differenti
M. Salerno
Tor Vergata
Laplace
5
Funzione gradino unitario
definizione
0 per t < 0
u-1(t) =
1 per t > 0
u-1(t)
{
il gradino
unitario èche
una
funzione
Schemi
equivalenti
utilizzano
discontinua
utile per analizzare
il gradino
unitario
circuiti contenenti interruttori,
generatore di tensione attivato
evitando di suddividere l’asse dei
per t = 0
tempi in più tratti separati
In molte applicazioni lo schema
la sinistra
funzionepuò
u-1(essere
t ) non
è definita
di
sostituito
per t = 0
con il seguente
1
t
Notazione
t=0
t= 0
Per il gradino
unitario è usato il simbolo
u-1(t) perché questa
di
A funzione fa parte A
un insieme numerabile di enti matematici,
indicati con il simbolo uk(t) (che verranno
B
B
definiti in seguito)
+
+
vg(t) uusate
(t) trattazioni sono spesso
-1(t)
Invgaltre
notazioni differenti
M. Salerno
Tor Vergata
Laplace
5
Funzione gradino unitario
definizione
0 per t < 0
u-1(t) =
1 per t > 0
u-1(t)
{
il gradino
unitario èche
una
funzione
Schemi
equivalenti
utilizzano
discontinua
utile per analizzare
il gradino
unitario
circuiti contenenti interruttori,
generatore
di
generatore
di tensione
corrente attivato
attivato
evitando
di suddividere
l’asse
dei
per
per ttratti
t == 00 separati
tempi in più
In molte applicazioni lo schema
la sinistra
funzionepuò
u-1(essere
t ) non
è definita
di
sostituito
per t = 0
con il seguente
1
t
Notazione
t=0
tt=
= 00 unitario è usato il simbolo
Per il gradino
u-1(t) perché questa
di
A funzione fa parte A
un insieme numerabile di enti matematici,
indicati con il simbolo uk(t) (che verranno
B
B
definiti in seguito)
+
+
ivgg(t)
(t) uu-1
(t)
(t) trattazioni sono spesso
-1(t)
Invigg(t)
altre
usate
notazioni differenti
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Gradino di ampiezza A,
traslato all’istante t0
f(t) = A u-1(t - t0 )
f(t) = A u-1(t - t0 )
f (t )
A
t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Gradino di
di un
ampiezza
Prodotto
gradinoA,
traslatoper
all’istante
t0
traslato
una funzione
g(t)
f(t)f(t)
= A= ug(t)
--1t0(t) - t0 )
-1(t u
La funzione g(t ) è
attivata per t > t0
f(t)
f(t)==g(t)
A u-1-1(t(t -- tt00))
g(
ff (t(t)
t ))
A
t0
t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Funzione di tipo sinusoidale
Attenzione: in tutte le applicazioni è essenziale
Gradino
di
ampiezza
A,
Prodotto
di
un
gradino
con inizio per t = 0
distinguere
funzione
f(t)
sinusoidale
f(t)f(t)
= A=laug(t)
--1t0(t
) -[ tandamento
)
-1(t u
0
traslato
all’istante
t
traslato per una funzione
g(t) per ogni t ] dalla funzione f0 (t) [ = 0 per t < 0 ]
0
{
f(t) = F cos (ω t + ϕ )
f0(t) = f(t) u-1( t )
La=funzione
g(tt) +è ϕ ) u ( t )
f0(t)
F cos (ω
-1
attivata per t > t0
f0(t) =f(t)
Ff(t)
cos
f(t)
ωg(t)
A
t +(uω-1
ϕ
(t
==
F(=
cos
t) +-u--1tϕt0(t)
-1(t
0)))
fg(
f0f (t(t)
(tt ))
A
t0
t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Funzione di tipo sinusoidale
Attenzione: in tutte le applicazioni è essenziale
La funzione
f(t)
si può
esprimere
Gradino
di
ampiezza
A,
Prodotto
di
un
gradino
con inizio per t = 0
distinguere
funzione
f(t)
sinusoidale
f(t)f(t)
= A=laug(t)
--1t0(t
) -[ tandamento
)
-1(t u
0
nel
modo
seguente
traslato
all’istante
t
traslato per una funzione
g(t) per ogni t ] dalla funzione f0 (t) [ = 0 per t < 0 ]
0
Infatti
f(t) = F cos (ω t + ϕ )
Laper
g(t
f0(t)
=funzione
Ft <cos
t)(+èt ϕ
t0 (ω
u-1
- t0))u=-10( ;t )f(t ) = A
f(t)
=
A
[1
u
(
t
t
)]
-1
0
f0(t) = f(t) u-1( t )
attivata
per t > t0 perut-1>( t0- t0 ) = 1 ; f(t) = 0
{
A
A
)))
f0(t) =f(t)
Ff(t)
cos
f(t)
=
ωg(t)
t u+(u-1ω-1
ϕ
(t
=
-A
( (t
--u-t-1t0ϕt0(t)
f(t)
=A=
F([1
cos
t) +
-1
0)]
fg(
f0f (t(t)
(tt ))
t0
t0 t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Funzione di tipo sinusoidale
Attenzione:
in tutte le applicazioni è essenziale
La
funzione
f(t)
si
esprimere
Si
può
disattivare
lapuò
La
funzione
f(t) ha la
Gradino
di
ampiezza
A,
Prodotto
di
un
gradino
con inizio per t = 0
distinguere
la
funzione
f(t)
sinusoidale
f(t)
=
A
u
(t
) -[ tandamento
f(t)
= g(t)
u-1t0(t
)
-1 espressione
0
nel
modo
seguente
funzione
g(t)
per
t
>
t
seguente
traslato
all’istante
t
traslato per una funzione
g(t) per ogni t ] dalla funzione f0 (t) [ = 0 per t < 0 ]
00
Infatti
f(t) = F cos (ω t + ϕ )
Laper
g(t
f0f(t)
(t)
==funzione
Fg(t)
t)(+èt( ϕ
t <cos
t0[1(ω
uu-1
- t ))u=)]0( ;t )f(t ) = A
f(t)
=
A
[1
u
(
t
t
)]
-1
0
-1 t -0 t0 -1
f0(t) = f(t) u-1( t )
attivata
per t > t0 perut-1>( t0- t0 ) = 1 ; f(t) = 0
{
A
A
t0
f(t)
=
)))
ff(t)
=f(t)
F
cos
f(t)
=
ωg(t)
tuu+(u-1ω
ϕ
(t
=
(t(t
--u-tt-1t00ϕt0(t)
)]
f(t)
=A[1
F([1
cos
t)-+
g(t)
- -A
0(t) =
-1
0)]
-1(-1
fg(
fg(t
f (t(t)
(tt)))
0f(t
t0
t0 t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Funzione
di tipo
La funzione
f(t) sinusoidale
Attenzione:
in tutte
f(t)La=funzione
A [u
( f(t)
tle) applicazioni
-hau-1
( t - Tè essenziale
)]
La
funzione
f(t)
si
esprimere
Si
può
disattivare
lapuò
la
Gradino
di
ampiezza
A,
-1
Prodotto
di
un
gradino
con
inizio perun
t =impulso
0
rappresenta
distinguere
funzione
f(t)
sinusoidale
f(t)f(t)
= A=laug(t)
) -[ tandamento
u--1t0(t
)
-1(t
0
nel
modo
seguente
funzione
g(t)
per
t
>
t
seguente
espressione
traslato
all’istante
t
perAuna
funzione
g(t) per ogni
0 0T
t ] dalla funzione f0 (t) [ = 0 per t < 0 ]
ditraslato
ampiezza
e durata
Infatti
Infatti
f(t) = F cos (ω t + ϕ )
Essendo presenti due discontinuità
per
t <funzione
0
: u-1g(t
( t ))=è0; u-1( t - T ) = 0; f(t) = 0
La
f
(t)
=
F
cos
(
ω
t (+1;
per
t
<
t
t( ϕ
-tut-0)()ttu=- -1
At [1
0f(t)
)]0( ;t )f(t ) = A
( per
t(t)
= 0=
e=per
=u
T -) (,usono
per 0=< tg(t)
< T :0[1
u-1(-u
tu
)-1=-1
-1)( t - t0 )]
-1 0 T ) = 0; f(t) = A
f0f(t)
f(t)
t
-1
attivata
per
= =00
0- ut0-1() t=
necessari due gradini unitari
per
t > Tt > t:0 per
u-1(utt -1
)>(= t1;
- T1);= f(t)
1; f(t)
{
A
A
A
t0
f(t)
=
g(t)
t0ϕt0(t)
ff(t)
=f(t)
cos
f(t)
=
tuu+(u-1ω
ϕ
(t
=
(t(t
--u-ttT
f(t)
=-1A[1
cos
t)-+
AF
[u
(F([1
tω
)- -A
)])))
=
g(t)
0(t) =
-1
-1
-1(-1
00
fg(
fg(t
f (t(t)
(tt)))
0f(t
t0
T t0 t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Funzione
di tipo
sinusoidale
Ladetermini
funzione
f(t)
Si
l’equazione
Attenzione:
in tutte
f(t)La=funzione
A [u
( f(t)
tle) applicazioni
-hau-1
( t - Tè essenziale
)]
La
funzione
f(t)
si
esprimere
Si
può
disattivare
lapuò
la
Gradino
di
ampiezza
A,
-1
Prodotto
di
un
gradino
con
inizio
perun
t =rimpulso
0
rappresenta
r(t)
della retta
distinguere
funzione
f(t)
sinusoidale
f(t)f(t)
= A=laug(t)
) -[ tandamento
u--1t0(t
)
-1(t
0
nel
modo
seguente
funzione
g(t)
per
t
>
t
seguente
espressione
traslato
all’istante
t
perAuna
funzione
g(t) per ogni
0 0T
t ] dalla funzione f0 (t) [ = 0 per t < 0 ]
ditraslato
ampiezza
e durata
Infatti
Infatti
f(t) = F cos (ω t + ϕ )
Essendo presenti due discontinuità
per
t <funzione
0
: u-1g(t
( t ))=è0; u-1( t - T ) = 0; f(t) = 0
La
f
(t)
=
F
cos
(
ω
t (+1;
per
t
<
t
t( ϕ
-tut-0)()ttu=- -1
At [1
0f(t)
)]0( ;t )f(t ) = A
( per
t(t)
= 0=
e=per
=u
T -) (,usono
per 0=< tg(t)
< T :0[1
u-1(-u
tu
)-1=-1
-1)( t - t0 )]
-1 0 T ) = 0; f(t) = A
f0f(t)
f(t)
t
-1
attivata
per
= =00
0- ut0-1() t=
necessari due gradini unitari
per
t > Tt > t:0 per
u-1(utt -1
)>(= t1;
- T1);= f(t)
1; f(t)
{
r(t) = a t + b
r(t) = a t + b | t = 0 = B
r(t) = a t + b | t = T = A
b = B ; a = (A - B) / T
A
A
A
A
B
t0
fg(
fg(t
f (t(t)
(tt)))
0f(t
r
f(t)
=
g(t)
t0ϕt0(t)
ff(t)
=f(t)
cos
f(t)
=
tuu+(u-1ω
ϕ
(t
=
(t(t
--u-ttT
f(t)
=-1A[1
cos
t)-+
AF
[u
(F([1
tω
)- -A
)])))
=
g(t)
0(t) =
-1
-1
-1(-1
00
t0
T T t0 t0
t
M. Salerno
Tor Vergata
Laplace
6
Funzione gradino unitario
Rappresentazione di funzioni discontinue mediante gradini unitari
Funzione
di tipo
sinusoidale
Ladetermini
funzione
f(t)
Si
l’equazione
Attenzione:
int /tutte
f(t)
=funzione
( f(t)
tleB]
) applicazioni
-ha
u-1
)]( t - T )]
La
funzione
f(t)
si
esprimere
f(t)
=
[(A
–AB)[u
T+
[u
uè -1essenziale
Si
può
disattivare
lapuò
La
la
Gradino
di
ampiezza
A,
-1
-1(( tt) -- T
Prodotto
di
un
gradino
con
inizio
perun
t =rimpulso
0
rappresenta
r(t)
della retta
distinguere
funzione
f(t)
sinusoidale
f(t)f(t)
= A=laug(t)
) -[ tandamento
u--1t0(t
)
-1(t
0
nel
modo
seguente
funzione
g(t)
per
t
>
t
seguente
espressione
traslato
all’istante
t
perAuna
funzione
g(t) per ogni
0 0T
t ] dalla funzione f0 (t) [ = 0 per t < 0 ]
ditraslato
ampiezza
e durata
Infatti
Infatti
Infatti
r(t)f(t)
= (A= –FB)cos
t / T+
(ωBt + ϕ )
Essendo presenti due discontinuità
per
0 : u:-1(ut-1g(t
=èu0;-1(ut-1-( T
t -) T= )0;= f(t)
0; f(t)
per(t)
tLa
< t=
0<funzione
)( =t )t0;
= 0= 0
)
f
F
cos
(
ω
+
ϕ
)
u
(
t
)
per
t
<
t
u
(
t
t
)
=
0
;
f(t
) r(t)
== A
At [1
-) (,usono
( t - t0 )] per
0f(t)
-1
=
g(t)
u
(
t
)]
0[1
-1
0-( tT
(f(t)
per
t(t)
=r(t)
0=
e=[u
per
=
T
per
0
<
t
<
T
:
u
(
t
)
=
1;
u
t
T
)
=
0;
f(t)
A
-1
0
<
t
<
T
:
u
(
t
)
=
1;
u
(
t
)
=
0;
f(t)
=
-1
0
-1
-1
f0=f(t)
f(t)
u
t
)
-1
-1
- u-1( t - T )]
-1( t ) -1
;= f(t)
f(t)
0- (ut0t-1-()T
necessari due gradini unitari
tT> Tt >
)>
t=-) T1
1; f(t)
perper
tattivata
>per
: tu:0 per
(ut-1)(u=tt -1
1;(= tu1;
= )1;
==0=00
{
-1
r(t)
r(t)==(A
a t– +B)bt / T+ B
r(t) = a t + b | t = 0 = B
r(t) = a t + b | t = T = A
b = B ; a = (A - B) / T
A
A
A
A
B
t0
fg(
fg(t
f (t(t)
(tt)))
0f(t
-1
f(t) = [(A – B) ff(t)
t (t)
/ T+
[u
(=
(t)-+
f(t)
=
g(t)
=f(t)
F
cos
f(t)
-1
tu-u+(uuω
ϕ-1
(t
)
=
(t(t
-t-u-t-tTtϕt0T(t)
f(t)
=A[1
cos
=
AB]
[u
(F([1
tω
)-t )-A
)])))]
=
g(t)
(-1
r
0
-1
-1-1-1
-1
00 0
t0
T T t0 t0
t
M. Salerno
Tor Vergata
Approssimanti
La funzione u-1(t ) non può essere
usata senza particolari accorgimenti
nell’analisi dei circuiti elettrici, in
quanto non è derivabile per t = 0.
In tutti gli altri istanti, u-1(t ) è
derivabile con derivata nulla.
Esempio: induttore
iL(t) = u-1(t)
corrente
vL(t) = L d iL(t)/dt
tensione
risulta:
per t =/ 0,
vL(t) = 0
per t = 0,
vL(t) non calcolabile
Laplace
7
M. Salerno
Tor Vergata
Laplace
7
Approssimanti
La funzione u-1(t ) non può essere
usata senza particolari accorgimenti
nell’analisi dei circuiti elettrici, in
quanto non è derivabile per t = 0.
In tutti gli altri istanti, u-1(t ) è
derivabile con derivata nulla.
Esempio: induttore
iL(t) = u-1(t)
corrente
vL(t) = L d iL(t)/dt
tensione
risulta:
per t =/ 0,
vL(t) = 0
per t = 0,
vL(t) non calcolabile
Approssimante di u-1(t )
u-1,ε (t )
{
derivabile per ogni t
lim u-1,ε (t ) = u-1 (t )
ε
0
con ε > 0
Definizione
Approssimante
dell’impulso unitario
d u-1,ε (t )
u0,ε (t ) =
dt
M. Salerno
Tor Vergata
Laplace
7
Approssimanti
La
funzionedi
u-1(tu)-1,non
può essere
Esempio
ε (t )
usata senza particolari accorgimenti
nell’analisi dei circuiti
0 per telettrici,
< 0 in
quanto non è derivabile per t = 0.
u-1, ε (t) =
t /ε per 0 < t < ε
In tutti gli altri istanti, u-1(t ) è
1 per t > ε
derivabile con derivata nulla.
u-1,ε ( t )
Esempio: induttore
1
ε
iL(t) = u-1(t)
corrente
vL(t) =decrescente
L d iL(t)/dt
tensione
risulta:
ε
t
per t =/ 0,
vL(t) = 0
per t = 0,
vL(t) non calcolabile
Approssimante di u-1(t )
u-1,ε (t )
{
derivabile per ogni t
lim u-1,ε (t ) = u-1 (t )
ε
0
con ε > 0
Definizione
Approssimante
dell’impulso unitario
d u-1,ε (t )
u0,ε (t ) =
dt
M. Salerno
Tor Vergata
Laplace
Approssimanti
La
funzionedi
u-1(tu)-1,non
può essere
Esempio
ε (t )
usata senza particolari accorgimenti
nell’analisi dei circuiti
0 per telettrici,
< 0 in
quanto non è derivabile per t = 0.
u-1, ε (t) =
t /ε per 0 < t < ε
In tutti gli altri istanti, u-1(t ) è
1 per t > ε
derivabile con derivata nulla.
u-1,ε ( t )
Esempio: induttore
1
ε
iL(t) = u-1(t)
corrente
vL(t) =decrescente
L d iL(t)/dt
tensione
risulta:
ε
t
per t =/ 0,
vL(t) = 0
per t = 0,
vL(t) non calcolabile
Approssimante
dell’impulso
Approssimante
di u-1(t )unitario
{{
u0,ε (t ) = d u-1,ε (t ) / dt
derivabile per ogni t
u-1,ε (t ) lim
0 per
ε)
u-1,tε<(t 0) e= tu>
-1 (t
u0, ε (t) = ε 0
1 /ε per 0 < t < ε
con ε > 0
Definizione u0,ε ( t )
1/ ε
Approssimante
A unitario
dell’impulso
du
ε -1,ε (t )
t
u0,ε (t ) =
Per ogni ε ,
dt
l’area A è uguale a 1
7
M. Salerno
Tor Vergata
Laplace
Approssimanti
La
funzionedi
u-1(tu)-1,non
può essere
Esempio
ε (t )
usata senza particolari accorgimenti
nell’analisi dei circuiti
0 per telettrici,
< 0 in
quanto non è derivabile
0 per t <per
0 t = 0.
{
t /ε per 0 < t < ε
u-u1,-1,ε (t)
ε (t)==
-t /ε uper
In tutti gli altri1 istanti,
–
e
-1(tε) tè > 0
1 per t >
derivabile con derivata nulla.
u-1,ε ( t )
Esempio: induttore
11
iL(t) = u-1(t)
corrente
ε
vL(t) =decrescente
L d iL(t)/dt
tensione
risulta:
ε
t
per t =/ 0,
vL(t) = 0
per t = 0,
vL(t) non calcolabile
Approssimante
dell’impulso
Approssimante
di u-1(t )unitario
{{
u0,ε (t ) = d u-1,ε (t ) / dt
derivabile per ogni t
u-1,ε (t ) lim
0 per
ε)
u-1,tε<(t 0) e= tu>
-1 (t
u0, ε (t) = ε 0
1 /ε per 0 < t < ε
con ε > 0
Definizione u0,ε ( t )
1/ ε
Approssimante
A unitario
dell’impulso
du
ε -1,ε (t )
t
u0,ε (t ) =
Per ogni ε ,
dt
l’area A è uguale a 1
7
M. Salerno
Tor Vergata
Laplace
Approssimanti
La
funzionedi
u-1(tu)-1,non
può essere
Esempio
ε (t )
usata senza particolari accorgimenti
nell’analisi dei circuiti
0 per telettrici,
< 0 in
quanto non è derivabile
0 per t <per
0 t = 0.
{
t /ε per 0 < t < ε
u-u1,-1,ε (t)
ε (t)==
-t /ε uper
In tutti gli altri1 istanti,
–
e
-1(tε) tè > 0
1 per t >
derivabile con derivata nulla.
u-1,ε ( t )
Esempio: induttore
11
iL(t) = u-1(t)
corrente
ε
vL(t) =decrescente
L d iL(t)/dt
tensione
risulta:
ε
t
per t =/ 0,
vL(t) = 0
per t = 0,
vL(t) non calcolabile
Approssimante
dell’impulso
Approssimante
di u-1(t )unitario
{{{
u0,ε (t ) = d u-1,ε (t ) / dt
derivabile per ogni t
u-1,ε (t ) lim
00 per
tt<
per
ε)
u-1,
(t00) e= tu>
ε<
-1 (t
(t)== ε 0
uu0,0,εε(t)
-t /ε0 per
<t<
(11 //εε )eper
t >ε 0
con ε > 0
Definizione u0,ε ( t )
1/
1/ εε
Approssimante
A unitario
dell’impulso
A
du
ε -1,ε (t )
t
u0,ε (t ) =
Perogni
ogniεε, ,
d t Per
l’areaAAèèuguale
ugualeaa11
l’area
7
M. Salerno
Tor Vergata
Laplace
Approssimanti
La
funzionedi
u-1(tu)-1,non
può essere
Esempio
ε (t )
usata C
senza
accorgimenti
t=0
+ particolari
nell’analisi dei circuiti
in
Rtelettrici,
0
per
<
0
i(t)
quanto nonVè0 derivabile
0 per t <per
0 t = 0.
{
t /ε per 0 < t < ε
u-u1,-1,ε (t)
ε (t)==
-t /ε uper
del1condensatore,
InNella
tuttiscarica
gli altri
istanti,
–
e
-1(tε) tè > 0
1 per t >
l’andamento della corrente i(t) è una
derivabile
con derivata nulla.
approssimante dell’impulso
{
u-1,0ε ( t )
Esempio:0induttore
per t <
i(t ) =
(V0 /R1)e - t /RC per t > 0
1
iL(t) = u-1(t)
corrente
ε
t
/RC
/ε ) e - t /ε
/R
)Led i (t)/dt
= (C V0 tensione
decrescente
0
v(V
(t)
=
L
L
risulta:
con
ε ε = RC
t
per t =/ 0,
vL(t) = 0
Si tratta dell’approssimante dell’impulso
per t = 0,
v (t) non calcolabile
unitario moltiplicataLper C V
0
Approssimante
dell’impulso
Approssimante
di u-1(t )unitario
{{{
u0,ε (t ) = d u-1,ε (t ) / dt
derivabile per ogni t
u-1,ε (t ) lim
00 per
tt<
per
ε)
u-1,
(t00) e= tu>
ε<
-1 (t
(t)== ε 0
uu0,0,εε(t)
-t /ε0 per
<t<
(11 //εε )eper
t >ε 0
con ε > 0
Definizione u0,ε ( t )
1/
1/ εε
Approssimante
A unitario
dell’impulso
A
du
ε -1,ε (t )
t
u0,ε (t ) =
Perogni
ogniεε, ,
d t Per
l’areaAAèèuguale
ugualeaa11
l’area
7
M. Salerno
Tor Vergata
Laplace
Impulso unitario
Per il gradino
Per l’impulso
u0 (t )
u-1 (t ) = lim u-1,ε (t )
ε
0
u0 (t ) = lim u0,ε (t )
ε
0
impulso unitario
o
impulso di Dirac
Proprietà fondamentale delle funzioni u0,ε (t)
∫
∞
∫
∞
u0, ε (t) d t = 1 per ogni ε > 0 , e quindi
u0, ε (t) d t = 1
lim
ε 0 -∞
-∞
Questa proprietà non è soddisfatta dall’impulso unitario u0 (t). Infatti :
∫
∞
∫
∞
lim u (t) d t = 0
u0(t) dt =
ε 0 0, ε
-∞
-∞
Questo risultato non è soddisfacente per le applicazioni
8
M. Salerno
Tor Vergata
Laplace
Impulso unitario
∞
Affinché
l’impulso di Dirac è definito nell’ambito di una
u
(t)
dt
=
1
lim matematica,
u-1,ε (t ) detta teoria delle
Per
il gradino 0 u-1 (t ) =teoria
0 distribuzioni.
risulti
ε
0
-∞
unitario
Tale teoria è un’estensione della teoria delle funzioni,impulso
in cui risultano
Per l’impulso
u0 (t ) = lim
u0,ε (t ) di derivata e di integrale
o
modificate
opportunamente
le definizioni
ε
0
impulso di Dirac
L’integrale di u0(t) è effettuato nel senso delle distribuzioni
∫
u (t )
Proprietà fondamentale delle funzioni u0,ε (t)
Definizione
Nell’ambito della teoria delle distribuzioni,
∞
unitario
u0(t) è definito
dalla
ε > 0 , e quindi
u0, ε (t) d t =l’impulso
1 per ogni
u0, ε (t) d t = 1
lim
ε 0 -∞
-∞
seguente relazione
∫
∞
{
∫
Questa proprietà non è soddisfatta dall’impulso unitario u0 (t). Infatti :
T
0
dt
limu0u(t)
u0(t) dt =
d t=
=0
0, ε (t)
ε
0
∫- ∞ ∫- ∞ - ∞
1
∞
∫
∞
per
per
T<0
T>0
Questo risultato non è soddisfacente per le applicazioni
8
M. Salerno
Tor Vergata
Laplace
Impulso unitario
∞ di u (t) non
Poiché
l’integrale
varia per
T < 0èedefinito
per T > nell’ambito
0, risulta: di una
Affinché
l’impulso
di Dirac
0
u
(t)
dt
=
1
lim matematica,
u-1,ε (t ) detta teoria delle
Per
il gradino 0 u-1 (t ) =teoria
0 distribuzioni.
risulti
ε
0 Al crescere di t , la variazione
del
-∞
u (t) = 0 per t < 0
unitario
valore
dell’integrale
in un
Tale0 teoria è un’estensione della teoria
delle
funzioni,impulso
inavviene
cui risultano
Per l’impulso
u0 (t ) = lim
u0,intorno
dell’origine
o
modificate
derivata e di
integrale
ε (t ) diinfinitesimo
0 per
t > 0ε le definizioni
u0(t) = opportunamente
0
(integrale
sensoimpulso
delle distribuzioni)
di Dirac
dellenel
distribuzioni
L’integrale di u0(t) è effettuato nel senso
∫
u (t )
impulso
di Dirac
Proprietà
fondamentale
delle funzioni
u0,ε (t)di Dirac è rappresentato come una
L’impulso
Nell’ambito
della
teoria delle distribuzioni,
∞ 0
∞
funzione nulla, con una discontinuità
unitario
u0(t) è definito
dalla
εnell’origine.
> 0 , e quindi
u0, ε 1(t) d t =l’impulso
1 per ogni
u0, ε (t) d t = 1
lim
ε 0 -∞
-∞
seguente relazione
Definizione
u (t)
∫
{
∫
discontinuità
è caratterizzata
dal valore
:
Questa proprietà non è soddisfatta La
dall’impulso
unitario
u0 (t). Infatti
T
dell’integrale, che è uguale a 1
∞
∞
t dt=0
lim 0u0, ε (t)
u0(t) dt =
ε 0
Tale valore non è l’altezza dell’impulso
-∞
- ∞- ∞
Questo risultato non è soddisfacente per le applicazioni
∫
∫
∫
0
u (t) dt =
1
per
per
T<0
T>0
8
M. Salerno
Tor Vergata
Laplace
9
Impulso unitario
Alcune proprietà dell’impulso unitario u0(t)
Impulso di ampiezza A,
traslato all’istante t0
h(t) = A u0(t - t0 )
L’ampiezza A è il valore dell’integrale, nel
senso delle distribuzioni, in un intorno di t0
∫δA u (t - t ) dt = A
0
0
δ è un qualunque intervallo
[anche infinitesimo]
comprendente t0
h(t )
h(t) = A u0(t - t0 )
A
t0
δ
t
M. Salerno
Tor Vergata
Laplace
9
Impulso unitario
Alcune proprietà dell’impulso unitario u0(t)
Impulso di un
ampiezza
A,
Prodotto
impulso
traslatoper
all’istante
t0
traslato
una funzione
f(t)
h(t) = Ah(t)
u0(t= -f(t)
t0 )u0(t - t0 )
A èh(t)
il valore
dell’integrale, nel
è un impulso
f(t) u0(t - t0 ) = f(t0) u0(t - L’ampiezza
t0 )
senso delle distribuzioni,
in un intorno
di ampiezza
f (t0 ) di t0
in particolare f(t) u0(t ) = f(0) u0(t )
∫δ∫Aδf(t)u (tu- (tt -) tdt) =dt A= f(t )
0
0 0
0
0
δ δè un
è unqualunque
qualunqueintervallo
intervallo
[anche
[ancheinfinitesimo]
infinitesimo]
comprendente
comprendentet0 t0
h(t )
h(t)
h(t)
= f(t)
= Auu00(t(t--t0t0))
f(t0 A
)
f(t)
t0
δδ
t
M. Salerno
Tor Vergata
Laplace
9
Impulso unitario
Alcune proprietà dell’impulso unitario u0(t)
Impulso di un
ampiezza
A,u0 (t)
Prodotto
impulso
traslato
all’istante
t
traslato
per
unaufunzione
f(t)
per
un gradino
-1(t)0
h(t) = Ah(t)
u0(t==-f(t)
h(t)
ut0-1)(tu0)(tu-0(tt0))
h(t)
impulso nel
A èh(t)
il valore
dell’integrale,
Per determinare
èè
unun
impulso
f(t) u0(t -l’ampiezza
t0 ) = f(t0non
) u0si(t può
- L’ampiezza
t0 usare
)
l’espressione u-1(t ) u0(t ) = u-1(0) usenso
0(t )
delle distribuzioni,
in un intorno
di t0
di
ampiezza
f
(t
)
0
in
particolare
f(t)
u
(t
)
=
f(0)
u
(t
)
perché il gradino non è 0definito per t =0 0
∫δ∫Aδf(t)u (tu- (tt -) tdt) =dt A= f(t )
0
0 0
0
0
δ δè un
è unqualunque
qualunqueintervallo
intervallo
[anche
[ancheinfinitesimo]
infinitesimo]
comprendente
comprendentet0 t0
h(t )
h(t)
h(t)
h(t)
==f(t)
=u-1A(tuu0)0(t(t
u0--(tt0t)0))
f(t0 A
)
f(t)
u-1(t )
t0
δδ
t
M. Salerno
Tor Vergata
Laplace
9
Impulso unitario
Alcune proprietà dell’impulso unitario u0(t)
Impulso di un
ampiezza
A,u0 (t)
Prodotto
impulso
traslato
all’istante
t
traslato
per
unaufunzione
f(t)
per
un gradino
-1(t)0
h(t) = Ah(t)
u0(t==-f(t)
h(t)
ut0-1)(tu0)(tu-0(tt0))
h(t)
impulso nel
A èh(t)
il valore
dell’integrale,
Per determinare
èè
unun
impulso
f(t) u0(t -l’ampiezza
t0 ) = f(t0non
) u0si(t può
- L’ampiezza
t0 usare
)
l’espressione u-1(t ) u0(t ) = u-1(0) usenso
0(t )
delle distribuzioni,
in
un intorno
di t0
di
ampiezza
f
(t
)
di
ampiezza
½
0
in
particolare
f(t)
u
(t
)
=
f(0)
u
(t
)
perché il gradino non è 0definito per t =0 0
∫δδu∫Aδf(t)(tu )(tuu-(t(tt )-)dttdt)==dt∫Aδ=u f(t(t )) d u (t ) = ½
-1 0
00 0
0
-1 0
-1
h(t )
h(t)
h(t)
h(t)
==f(t)
=u-1A(tuu0)0(t(t
u0--(tt0t)0))
f(t0 A
)
f(t)
u-1(t )
= ½ [ u-12(t ) ] ba = ½
a
δ δè un
è unqualunque
qualunqueintervallo
intervallo
[anche
[ancheinfinitesimo]
infinitesimo]
comprendente
t0 t0
comprendente
comprendente
l’origine
b
δ
t0
δδ
t
M. Salerno
Tor Vergata
Laplace
9
Impulso unitario
Alcune proprietà dell’impulso unitario u0(t)
Impulso di un
ampiezza
A,u0 (t)
Prodotto
impulso
traslato
all’istante
t
traslato
per
unaufunzione
f(t)
per
un gradino
-1(t)0
h(t) = Ah(t)
u0(t==-f(t)
h(t)
ut0-1)(tu0)(tu-0(tt0))
h(t)
impulso nel
A èh(t)
il valore
dell’integrale,
Per determinare
èè
unun
impulso
f(t) u0(t -l’ampiezza
t0 ) = f(t0non
) u0si(t può
- L’ampiezza
t0 usare
)
l’espressione u-1(t ) u0(t ) = u-1(0) usenso
0(t )
delle distribuzioni,
in
un intorno
di t0
di
ampiezza
f
(t
)
di
ampiezza
½
0
in
particolare
f(t)
u
(t
)
=
f(0)
u
(t
)
perché il gradino non è 0definito per t =0 0
∫∫
∫
Estensione della
uA-1f(t)
(tu0)(tuu-00(t
==
u-1f(t
(t0)) d u-1(t ) =
(tt0)-)dt
tdt
dt A=
0 ) gradino
definizione
di
δδ δ
δ
½
b
2
0
per
t
<
0
= ½ [ u-1 (t ) ] a = ½
{
u-1 ( t ) = ½ per t = 0
1 per t > 0
δ δè un
è unqualunque
qualunqueintervallo
intervallo
in
[anche
[ancheinfinitesimo]
infinitesimo]
comprendente
comprendente
comprendente
questo
modol’origine
sit0 tha:
h(t)
0
h(t )
h(t)
h(t)
h(t)
==f(t)
=u-1A(tuu0)0(t(t
u0--(tt0t)0))
u-1(t )
f(t0 A
)
½
a
b
δ
f(t)
u-1(t )
t0
δδ
= u-1(t ) u0(t ) = u-1(0 ) u0(t ) = 1/2 u0(t )
t
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
t=0
EC = ½ CV02 assorbita da R
i (t)
Q
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
t=0
EC = ½ CV02 assorbita da R
i (t)
Q
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
V0
C
+
i(t)
t=0
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
i (t)
Q
t=0
EC = ½ CV02 assorbita da R
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
V0
C
+
v(t)
i(t)
I
t=0
v (t)
v(t) = V0 [1 – u-1(t)]
V0
t
Sono presenti due componenti ideali: il condensatore e l’interruttore I
L’analisi del circuito è possibile solo nell’ambito della teoria delle
distribuzioni, utilizzando il gradino u-1(t) e l’impulso u0(t)
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
i (t)
Q
t=0
EC = ½ CV02 assorbita da R
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
V0
C
+
v(t)
i(t)
I
t=0
v (t)
v(t) = V0 [1 – u-1(t)]
V0
t
Sono
componenti
i(t) =presenti
- C dv/dtdue
=-C
d V0 [1 – u-1ideali:
(t)] /dtil condensatore e l’interruttore I
= C teoria
V0 u0(t)
L’analisi del
circuitolaè derivata
possibile
nell’ambitoi(t)
della
delle
effettuando
di usolo
-1(t)
distribuzioni,
utilizzando
il gradino u-1(t) e l’impulso u0(t)
nel senso
delle distribuzioni
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
i (t)
Q
t=0
EC = ½ CV02 assorbita da R
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
V0
C
+
v(t)
i(t)
I
t=0
iv(t)
(t)
v(t) = V0 [1 – u-1(t)]
i(t) = C V0 u0(t)
V0
t
Sono
componenti
i(t) =presenti
- C dv/dtdue
=-C
d V0 [1 – u-1ideali:
(t)] /dtil condensatore e l’interruttore I
= C teoria
V0 u0(t)
L’analisi del
circuitolaè derivata
possibile
nell’ambitoi(t)
della
delle
effettuando
di usolo
-1(t)
distribuzioni,
utilizzando
il gradino u-1(t) e l’impulso u0(t)
nel senso
delle distribuzioni
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
i (t)
Q
t=0
EC = ½ CV02 assorbita da R
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
V0
C
+
v(t)
i(t)
iv(t)
(t)
I
v(t) = V0 [1 – u-1(t)]
Q
i(t) = C V0 u0(t)
V0
t=0
Q = C V0
t
EC = ½ CV0 assorbita da I
2
∫
∞
∫
∞
Energia
assorbita
Sono
componenti
ideali:
i(t) =presenti
-C
dv/dtdue
=-C
d V0 [1 – uE
/dtil condensatore e l’interruttore I
-1(t)]
I = p(t) dt = v(t) i(t) dt =
dall’interruttore
∞
∞
∞i(t)
= C teoria
V0 u0(t)
L’analisi del
circuitolaè derivata
possibile
nell’ambito
della
delle
effettuando
di usolo
-1(t)
2
2
= Vdistribuzioni
– u-1(t)] CV
dt = CV0u [1
0[1
0 ue
0(t)
l’impulso
(t)– ½ ] = ½ CV0
distribuzioni,
utilizzando
il gradino
u (t)
nel senso
delle
∫∞
-1
0
M. Salerno
Tor Vergata
Laplace
10
Esempio
V0
C
+
R
V0 /R
i(t)
i (t)
Q
t=0
EC = ½ CV02 assorbita da R
t
i(t) = (V0 / R) e − t / RC u-1 (t) ;
Q = CV0
Questa soluzione vale per ogni valore di R , ma non per R = 0
V0
C
+
v(t)
i(t)
iv(t)
(t)
I
v(t) = V0 [1 – u-1(t)]
Q
i(t) = C V0 u0(t)
V0
t=0
Q = C V0
t
EC = ½ CV0 assorbita da I
2
∫
∞
∫
∞
Questa
soluzione,
congrua
conillacondensatore
precedente, vale
solo
Energia
assorbita
Sono
componenti
ideali:
e l’interruttore
I
i(t) =presenti
-C
dv/dtdue
=-C
d V0 [1 – uE
(t)]
/dt
=
p(t)
dt
=
v(t)
i(t)
dt
=
-1 I
nell’ambito
della teoria ∞delle distribuzioni.
dall’interruttore
∞
∞i(t)
= C teoria
V0 u0(t)
L’analisi del
circuito
è
possibile
nell’ambito
della
delle
effettuando la derivata di usolo
-1(t)
2
= Vdistribuzioni
–l’interruttore
u-1(t)] CV
dt = può
CV0uassorbire
[1
½ CV02
Se i(t) [ onel
v(t)senso
] è impulsiva,
ideale
0[1
0 ue
0(t)
l’impulso
(t)– ½ ] =energia
distribuzioni,
utilizzando
il gradino
u (t)
delle
∫∞
-1
0
M. Salerno
Tor Vergata
Laplace
11
Distribuzioni successive
Derivate successive dell’impulso unitario
L’impulso unitario può essere
derivato infinite volte, nel
senso delle distribuzioni
Esempio:
u1(t)
doppietto unitario
u1(t) = d u0(t) / dt
Notazione
d uk-1(t)
----------, k = 1, 2, …
uk(t) =
dt
1/ε
Approssimanti
u1,ε (t) = d u0,ε (t) / dt
u0,ε (t)
u1,ε (t)
1/ε
ε
ε
t
t
Al diminuire di ε il doppietto è assimilabile a due
impulsi di area opposta nell’intorno dell’origine
−1/ε
M. Salerno
Tor Vergata
Laplace
11
Distribuzioni successive
Derivate successive dell’impulso unitario
L’impulso unitario può essere
derivato infinite volte, nel
senso delle distribuzioni
Notazione
d uk-1(t)
----------, k = 1, 2, …
uk(t) =
dt
Esempio:successivi
u1(t) del gradino u0,ε (t)
Integrali
doppietto
Il gradinounitario
unitario può essere
1/ε
infinite volte, rimanendo
uintegrato
1(t) = d u0(t) / dt
nell’ambito delle funzioni
Esempio: uu-2
(t)
1,ε (t)
rampa1/ε
unitaria
u-2 (t)
Approssimanti
1
Notazione
ε
t
u1,ε (t) = d u0,εt (t) / dt
u-k-1(t) = u-k(τ) Al
dτdiminuire
, k = 1,
di ε2,il …
doppietto è assimilabile a due
-∞
impulsi di area opposta nell’intorno dell’origine
∫
ε
t
1
−1/ε
t
M. Salerno
Tor Vergata
Laplace
Distribuzioni successive
Derivate successive dell’impulso unitario
L’impulso unitario può essere
derivato infinite volte, nel
senso delle distribuzioni
Notazione
d uk-1(t)
----------, k = 1, 2, …
uk(t) =
dt
Esempio:successivi
u1(t) del gradino
Integrali
Esempio: uu-2
(t)
integrazioneu0,ε (t)
1,ε (t)
derivazione
doppietto
Il gradinounitario
unitario può essere
rampa1/ε
unitaria
1/ε
rimanendo
uintegrato
= duuinfinite
(t) / dtvolte,
1(t)…..
0(t)
(t) …..
u-1(t)
u0(t)
u1(t)
uu-22(t)
-2 delle funzioni
nell’ambito
ε
…..
rampa
gradino
impulso
doppietto tripletto
…..
Approssimanti
1
Notazione
ε
t
t
u1,ε (t) = d u0,εt (t) / funzioni
dt
distribuzioni
−1/ε
u-k-1(t) = u-k(τ) Al
dτdiminuire
, k = 1,
di ε2,il …
doppietto è assimilabile a due
1
nulle
< 0 di area opposta
nullenell’intorno
per t =/ 0dell’origine
t
- ∞per timpulsi
∫
11
M. Salerno
Tor Vergata
Laplace
Analisi nel dominio di Laplace
Circuiti senza
memoria
Circuiti con
memoria
Circuiti privi di
condensatori, induttori,
induttori accoppiati
Circuiti contenenti
condensatori, induttori,
induttori accoppiati
Analisi nel dominio del tempo
equazioni
algebriche
equazioni
differenziali
L’analisi di circuiti con memoria
è differente dall’analisi di circuiti senza memoria
ed è molto complessa
12
M. Salerno
Tor Vergata
Laplace
Analisi nel dominio di Laplace
Circuiti senza
memoria
Circuiti con
memoria
Circuiti privi di
condensatori, induttori,
induttori accoppiati
Circuiti contenenti
condensatori, induttori,
induttori accoppiati
Analisi nel
nel dominio
dominio di
delLaplace
tempo
Analisi
equazioni
algebriche
equazioni
differenziali
algebriche
L’analisi di circuiti con memoria
è differente
è simile all’analisi
dall’analisi
di di
circuiti
circuiti
senza
senza
memoria
memoria
ed
edèèmolto
moltosemplificata
complessa
12
M. Salerno
Tor Vergata
Laplace
Analisi nel dominio di Laplace
Circuiti con
Circuiti
senza
Metodo
della trasformata
di
memoria Laplace memoria
Circuiti privi di
condensatori, induttori,
induttori accoppiati
Circuiti contenenti
condensatori, induttori,
induttori accoppiati
1. Definizione
2. Trasformate
elementari
Analisi
nel
dominio
delLaplace
tempo
Analisi nel dominio di
3.equazioni
Proprietà
equazioni
4.algebriche
Applicazione ai componenti
differenziali
algebriche
elettrici
L’analisi di circuiti con memoria
è5.
differente
è simile
all’analisi
dall’analisi
di di
circuiti
circuiti
senza
senza
memoria
memoria
Antitrasformazione
ed
edèèmolto
moltosemplificata
complessa
12
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: definizione
Trasformata di Laplace
1. Definizione
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
componenti elettrici
5. Antitrasformazione
13
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: definizione
Trasformata di Laplace
1. Definizione
T
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
0
componenti elettrici
5. Antitrasformazione
F(s) = lim
T ∞
∫
Notazione
f(t) e-s t dt
F(s) = L [ f(t) ]
F(s) L-trasformata di f(t)
Nell’analisi dei circuiti, tutte le grandezze elettriche, tensioni e correnti,
sono sostituite con le rispettive L-trasformate
V(s) = L [ v(t) ]
I(s) = L [ i(t) ]
Notazione
Con la lettera minuscola, p.es. v(t), è indicata la
grandezza nel tempo, con la lettera maiuscola, p.
es. V(s), la rispettiva trasformata
La variabile di Laplace s non ha un immediato significato fisico e viene
considerata come una variabile complessa
13
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: definizione
Trasformata di Laplace
1. Definizione
T
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
0
componenti elettrici
5. Antitrasformazione
F(s) = lim
T ∞
∫
Notazione
f(t) e-s t dt
F(s) = L [ f(t) ]
F(s) L-trasformata di f(t)
Nell’analisi
dei circuiti,
tutte le reale
grandezze elettriche, tensioni e correnti,
f(t) : funzione
di variabile
sono sostituite con le rispettive L-trasformate
F(s) : funzione di variabile complessa
Notazione
T
V(s) = L [ v(t) ]
Dimensioni
t dt
V(s) = Con
lim la lettera
v(t) e-sminuscola,
p.es. v(t), è indicata la
∫
Tgrandezza
∞ 0 nel tempo, con la lettera maiuscola, p.
I(s) = L [ i(t) ]
V(s), la rispettiva
trasformata
tempo
variabile s : sec -1 (s -1) es.adimensionale
V(s) : volt . sec ( V s )
La variabile di Laplace s non ha unanalogamente
immediato significato
fisico
I(s) : ampère
. sece (viene
As)
considerata come una variabile complessa
13
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: definizione
Trasformata di Laplace
1. Definizione
T
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
0
componenti elettrici
5. Antitrasformazione
F(s) = lim
T ∞
∫
Notazione
f(t) e-s t dt
F(s) = L [ f(t) ]
F(s) L-trasformata di f(t)
piano s tensioni
Proprietà
del
limite
per
Nell’analisi
dei circuiti,
tutteTle reale
grandezze
ω e= correnti,
Im[s]
f(t) : funzione
di variabile
∞ elettriche,
sono sostituite con le rispettive L-trasformate
F(s)
funzione
complessa
Se il :limite
esistedi
edvariabile
è finito per
s = s0
allora esiste ed è finitoNotazione
per ogniT s
V(s) = L [ v(t) ]
Dimensioni
tale cheV(s)
Re[ =
s ]lim
> Re[ s v(t)
] e-s t dt
∫
Con la lettera
minuscola, p.es.
v(t), è indicata la
0
α
σ = Re[s]
Tgrandezza
∞ 0 nel tempo, con la lettera maiuscola,
p.
di Re[ s0 ] :
I(s) = LEstremo
[ i(t) ] inferiore
-1) es.adimensionale
V(s), la
trasformata
tempo
α rispettiva
variabile sascissa
: sec -1di(sconvergenza
V(s) : volt . sec ( V s )
LaSe
variabile
di esiste
Laplace
immediato significato
fisico
e (viene
il limite non
o nons ènon
finitoha
perunanalogamente
I(s) : ampère
.
sec
As)
semipiano di convergenza
alcun
valore
di
s
,
f(t)
non
è
L-trasformabile
considerata come una variabile complessa
13
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: definizione
Trasformata di Laplace
1. Definizione
T
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
00 componenti elettrici
5. Antitrasformazione
F(s) = lim
T ∞
∫
Notazione
f(t) e-s t dt
F(s) = L [ f(t) ]
F(s) L-trasformata di f(t)
piano
s tensioni
Proprietà
del
limite
per
Nell’analisi
deidicircuiti,
tutte
grandezze
elettriche,
ω eperché
= correnti,
Im[s] i
f(t) : funzione
variabile
reale
∞
L’andamento
f(t)diper
t < 0Tle
non
dà contributo
all’integrale,
sono
sostituite con
leesclusi
rispettive L-trasformate (trasformata unilatera).
tempi
sono
F(s)
:limite
funzione
di
complessa
Se il negativi
esiste
edvariabile
è finito dall’integrazione
per
s = s0
Conviene
considerare
f(t) Notazione
=per
0 per
allora
esiste ed è finito
ognitT <s 0
V(s) = L [ v(t) ]
Dimensioni
t dt
tale cheV(s)
Re[ =
s Con
]lim
> Re[
s0v(t)
] e-sminuscola,
la lettera
p.es.
la
α v(t), è indicata
σ = Re[s]
∫
Calcolo Estremo
dell’integrale
nel
inferiore di
Re[senso
s ] : delle distribuzioni
Tgrandezza
∞ 0 nel tempo, con la lettera maiuscola, p.
0
I(s) = L [ i(t) ]
-1
-1
V(s), la
trasformata
tempo
di(sconvergenza
α rispettiva
variabile
sascissa
: sec all’integrale
) es.adimensionale
V(s)
: volt . sec (per
V s t) = 0
contribuiscono
eventuali
impulsi,
in particolare
LaSe
variabile
di esiste
Laplace
ha
immediato significato
e (viene
il limite non
o nons ènon
perunanalogamente
- fisico
I(s)con
: ampère
.
sec
As)
l’estremo
inferiore
difinito
integrazione
è indicato
0
semipiano di convergenza
alcun
valore
di
s
,
f(t)
non
è
L-trasformabile
considerata come una variabile complessa
13
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: definizione
Trasformata di Laplace
1. Definizione
T
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
00 componenti elettrici
5. Antitrasformazione
F(s) = lim
T ∞
∫
Notazione
f(t) e-s t dt
F(s) = L [ f(t) ]
F(s) L-trasformata di f(t)
piano
s tensioni
Antitrasformata
: diper
Proprietà
del
limite
per
Nell’analisi
deidicircuiti,
tutte
grandezze
elettriche,
ω eperché
= correnti,
Im[s] i
f(t) : funzione
variabile
reale
∞
L’andamento
f(t)
t < 0Tle
non
dà contributo
all’integrale,
Notazione
sonooperatore
sostituiteinverso,
con le rispettive L-trasformate
tempi
sono
esclusi
(trasformata unilatera).
F(s)
:limite
funzione
di
complessa
Se il negativi
esiste
edvariabile
è finito dall’integrazione
per
s = s0
perallora
passare
f(t)
Conviene
considerare
f(t)aNotazione
=per
0 per
esisteda
ed F(s)
è finito
ognitT <s 0
V(s) = L [ v(t) ]
Dimensioni
t dt
tale cheV(s)
Re[ =
s Con
]lim
> Re[
s0v(t)
] e-sminuscola,
la lettera
p.es.
la
α v(t), è indicata
Esiste una formula integrale,
σ = Re[s]
1
f(t) = L [ F(s) ]
∫
Calcolo Estremo
dell’integrale
nel
inferiore di
Re[senso
s ] : delle distribuzioni
Tgrandezza
∞ 0 nel tempo, con la lettera maiuscola, p.
0
I(s)utilizzata
= L [ i(t)nell’analisi
] -1 -1 dei
poco
circuiti
V(s), la
trasformata
tempo
di(sconvergenza
α rispettiva
variabile
sascissa
: sec all’integrale
) es.adimensionale
V(s)
: volt . sec (per
V s t) = 0
contribuiscono
eventuali
impulsi,
in particolare
LaSe
variabile
di esiste
Laplace
immediato significato
e (viene
il limite non
o nons ènon
finitoha
perunanalogamente
- fisico
I(s)
:
ampère
.
sec
As)
l’estremo
inferiore
di
integrazione
è
indicato
con
0
semipiano
diinconvergenza
Metodi
operativi
di
antitrasformazione
di
Laplace
saranno
descritti
seguito
alcun
valore
di
s
,
f(t)
non
è
L-trasformabile
considerata come una variabile complessa
13
M. Salerno
Tor Vergata
Trasformate elementari
Trasformata di Laplace
1. Definizione
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
componenti elettrici
5. Antitrasformazione
Laplace
14
M. Salerno
Laplace
Trasformate elementari
Tor Vergata
Trasformata di Laplace
f(t) = u-1(t)
Gradino
1. Definizione
2. Trasformate Telementari
3. Proprietà
F(s)
= lim u-1(t) e-s t dt
T ∞
4. Applicazione
0 ai
componenti
elettrici
T
5. Antitrasformazione
-s t
∫
= lim
T
[
∞
= lim
T
per
∫
∞ 0
e
1 e-s t ]T
s
0
[
∞
dt = lim
T
1 -s T
1
e
]
+
s
s
= 1s
Re[ s ] > 0
ascissa di convergenza α = 0
14
F(s) = lim
T
∞
T
∫0
f(t) e-s t dt
-
M. Salerno
Tor Vergata
Laplace
Trasformate elementari
Trasformata di Laplace
f(t) =f(t)
u-1(t)
= e a t u-1(t)
Esponenziale
Gradino
1. Definizione
a : reale o complesso
2. Trasformate Telementari
3. Proprietà
F(s)
= lim Tu-1(t) e-s t dt
4. Applicazione
F(s)
=T lim∞ 0 uai- -1(t) e-s t ea t dt
T ∞
componenti
T 0 elettrici
5. Antitrasformazione
1 -s t T
T -s t
∫∫
∫∫
= lim e dt -=(s-a)
limt [ s e 1]
=T lim∞ 0u-1(t) e T ∞dt = s - a0
T ∞
0
1 -s T
1 = 1
=
lim
[
e
]
+
per
Re[ ss- a ] > 0 ; Re[
s s ] >sRe[ a ]
T ∞
ascissa
convergenza
α = Re [ a ]
per diRe[
s]>0
l’integrale
è identico
a quello relativo
ascissa di
convergenza
α = 0 al
gradino, eccetto la sostituzione di s con s-a
14
F(s) = lim
T
T
∞
∫0
f(t) e-s t dt
-
Trasformate
L [ u-1(t) ]
= 1s
M. Salerno
Tor Vergata
Laplace
Trasformate elementari
Trasformata di Laplace
f(t)==uf(t)
= e a t u-1(t)
Esponenziale
Gradino
f(t)
Impulso
-1(t)
0u(t)
1. Definizione
a : reale o complesso
Telementari
2. TrasformateT
F(s)
== lim
u
ee-s-st tdtdt
Tu0-1(t)
3. Proprietà
F(s)
lim
(t)
∞
-∞ 00 u
4. Applicazione
ai-1(t) e-s t ea t dt
F(s)
=TT lim
T ∞
componenti
0 -elettrici
-s t
T
= Tlim
e
t=0 = 11 -s t T
5. Antitrasformazione
-s t
∫∫
∫
∫[
]
= lim T e ∞dt -=(s-a)
limt [ s e 1]
=T lim∞ 0u-1(t) e T ∞dt = s - a0
T
per ∞
ogni0 valore di s
1 -s T
1α = =- 1
ascissa
di
convergenza
=
lim
[
e
]
+
per
Re[ ss- a ] > 0 ; Re[
>sRe[ a ]
s s]∞
T ∞
ascissa
convergenza
α delle
= Redistribuzioni
[a]
l’integrale
calcolato
per dièRe[
s ] > nel
0 senso
èl’integrale
essenzialeèche
l’estremo
inferiore
di integrazione
identico
a quello
relativo
ascissa
di
convergenza
α
=
0 al
sia
0
gradino, eccetto la sostituzione di s con s-a
14
F(s) = lim
T
∞
T
∫0
f(t) e-s t dt
-
Trasformate
L [ u-1(t) ] = 1s
1
L [eat u-1(t)] = ----s-a
M. Salerno
Tor Vergata
Laplace
Trasformate elementari
Trasformata di Laplace
f(t)==uf(t)
= e a t u-1(t)
Esponenziale
Gradino
f(t)
Impulso
-1(t)
0u(t)
1. Definizione
a : reale o complesso
Telementari
2. TrasformateT
F(s)
== lim
u
ee-s-st tdtdt
Tu0-1(t)
3. Proprietà
F(s)
lim
(t)
∞
-∞ 00 u
4. Applicazione
ai-1(t) e-s t ea t dt
F(s)
=TT lim
T ∞
componenti
0 -elettrici
-s t
T
= Tlim
e
t=0 = 11 -s t T
5. Antitrasformazione
-s t
∫∫
∫
∫[
]
= lim T e ∞dt -=(s-a)
limt [ s e 1]
=T lim∞ 0u-1(t) e T ∞dt = s - a0
T
per ∞
ogni0 valore di s
1 -s T
1α = =- 1
ascissa
di
convergenza
=
lim
[
e
]
+
per
Re[ ss- a ] > 0 ; Re[
>sRe[ a ]
s s]∞
T ∞
ascissa
convergenza
α delle
= Redistribuzioni
[a]
l’integrale
calcolato
per dièRe[
s ] > nel
0 senso
èl’integrale
essenzialeèche
l’estremo
inferiore
di integrazione
identico
a quello
relativo
ascissa
di
convergenza
α
=
0 al
sia
0
gradino, eccetto la sostituzione di s con s-a
14
F(s) = lim
T
∞
T
∫0
f(t) e-s t dt
-
Trasformate
L [ u-1(t) ] = 1s
1
L [eat u-1(t)] = ----s-a
L [u0(t)] = 1
Queste sono le uniche
trasformate di cui sarà effettuato
il calcolo dell’integrale
M. Salerno
Tor Vergata
Laplace
Trasformate elementari
14
F(s) = lim
T
∞
T
∫0
f(t) e-s t dt
-
Trasformata di Laplace
f(t)==uf(t)
= e a t u-1(t)
Esponenziale
Gradino
f(t)
Impulso
Antitrasformate
-1(t)
0u(t)
Trasformate
1
1
∫
L [ s ] u (t)
∫[ ]
1
1
T e ----∞
= lim
dt
=(s-a)
lim
[
e (t)
]
1
L
[
]
e
u
=
t
s
∫
=T lim∞ ∫0u-1s(t)-ae T ∞dt = -1s - a0
T
per ∞
ogni0 valore di s
1-1 -s T
1α = =- 1
ascissa
di
convergenza
=
lim
[
e
]
+
Ls - a [] >10];=Re[u s(t)] ∞> Re[ a ]
per
Re[
L [ u-1(t) ] = 1s
1
L [eat u-1(t)] = ----s-a
L [u0(t)] = 1
1. Definizione
a : reale o complesso
Telementari
2. TrasformateT
F(s)
== lim
u
ee-s-st tdtdt
Tu0-1(t)
3. Proprietà
F(s)
lim
(t)
=
∞
-∞ 00 u
4. Applicazione
ai-1(t) e-s t e-a1t dt
F(s)
=TT lim
T ∞
componenti
0 -elettrici
-s t
T
= 11 -s t T
= Tlim
e
t=0 at
5. Antitrasformazione
-s t
T
∞
s
s 0
s
ascissa
convergenza
α delle
= Redistribuzioni
[a]
l’integrale
calcolato
per dièRe[
s ] > nel
0 senso
èl’integrale
essenzialeèche
l’estremo
inferiore
di integrazione
identico
a quello
relativo
ascissa
di
convergenza
α
=
0 al
sia
0
gradino, eccetto la sostituzione di s con s-a
Queste sono le uniche
trasformate di cui sarà effettuato
il calcolo dell’integrale
M. Salerno
Tor Vergata
Laplace
Trasformate elementari
14
F(s) = lim
T
∞
T
∫0
f(t) e-s t dt
-
Trasformata di Laplace
f(t)==uf(t)
= e a t u-1(t)
Esponenziale
Gradino
f(t)
Impulso
Antitrasformate
-1(t)
0u(t)
Trasformate
1
1
∫
L [ s ] u (t)
∫[ ]
1
1
T e ----∞
= lim
dt
=(s-a)
lim
[
e (t)
]
1
L
[
]
e
u
=
t
s
∫
=T lim∞ ∫0u-1s(t)-ae T ∞dt = -1s - a0
T
per ∞
ogni0 valore di s
1-1 -s T
1α = =- 1
ascissa
di
convergenza
=
lim
[
e
]
+
Ls - a [] >10];=Re[u s(t)] ∞> Re[ a ]
per
Re[
L [ u-1(t) ] = 1s
1
L [eat u-1(t)] = ----s-a
L [u0(t)] = 1
1. Definizione
a : reale o complesso
Telementari
2. TrasformateT
F(s)
== lim
u
ee-s-st tdtdt
Tu0-1(t)
3. Proprietà
F(s)
lim
(t)
=
∞
-∞ 00 u
4. Applicazione
ai-1(t) e-s t e-a1t dt
F(s)
=TT lim
T ∞
componenti
0 -elettrici
-s t
T
= 11 -s t T
= Tlim
e
t=0 at
5. Antitrasformazione
-s t
T
∞
s
s 0
s
ascissa
dièRe[
convergenza
α delle
= Redistribuzioni
[a]
l’integrale
calcolato
senso
per Una
s ] > nel
0antitrasformata
ulteriore
èl’integrale
essenziale
l’estremo
inferiore
di :integrazione
èche
identico
aèquello
relativo
d’interesse
la
seguente
ascissa
di
convergenza
α
=
0 al
sia
0
gradino, eccetto la sostituzione di s con s-a
Queste sono le uniche
trasformate di cui sarà effettuato
il calcolo dell’integrale
M. Salerno
Laplace
Trasformate elementari
Tor Vergata
14
F(s) = lim
T
∞
T
∫0
f(t) e-s t dt
-
Trasformata di Laplace
f(t)==uf(t)
= e a t u-1(t)
Esponenziale
Gradino
f(t)
Impulso
Antitrasformate
-1(t)
0u(t)
Trasformate
1
1
∫
L [ s ] u (t)
∫[ ]
1
1
T e ----∞
= lim
dt
=(s-a)
lim
[
e (t)
]
1
L
[
]
e
u
=
t
s
∫
=T lim∞ ∫0u-1s(t)-ae T ∞dt = -1s - a0
T
per ∞
ogni0 valore di s
1-1 -s T
1α = =- 1
ascissa
di
convergenza
=
lim
[
e
]
+
Ls - a [] >10];=Re[u s(t)] ∞> Re[ a ]
per
Re[
L [ u-1(t) ] = 1s
1
L [eat u-1(t)] = ----s-a
L [u0(t)] = 1
1. Definizione
a : reale o complesso
Telementari
2. TrasformateT
F(s)
== lim
u
ee-s-st tdtdt
Tu0-1(t)
3. Proprietà
F(s)
lim
(t)
=
∞
-∞ 00 u
4. Applicazione
ai-1(t) e-s t e-a1t dt
F(s)
=TT lim
T ∞
componenti
0 -elettrici
-s t
T
= 11 -s t T
= Tlim
e
t=0 at
5. Antitrasformazione
-s t
T
∞
s
s 0
s
ascissa
dièRe[
= Redistribuzioni
[a]
l’integrale
calcolato
senso
1 α delle
per
s ] > nel
0antitrasformata
1convergenza
-1 Una
ulteriore
n-1 eat u (t)
=
t
nl’estremo
-1
èl’integrale
essenziale
1)!
(sd’interesse
-èche
a)
identico
aè(n
quello
relativo
al
la-inferiore
seguente
ascissa
di
convergenza
α =di0:integrazione
L
[------ ] -----
sia
0 - eccetto la sostituzione di s con s-a
gradino,
Queste sono le uniche
trasformate di cui sarà effettuato
il calcolo dell’integrale
M. Salerno
Tor Vergata
Laplace
Trasformata di Laplace: proprietà
Trasformata di Laplace
1. Definizione
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
componenti elettrici
5. Antitrasformazione
15
M. Salerno
Laplace
Trasformata di Laplace: proprietà
Trasformata di Laplace
Linearità
1. Definizione
Tor Vergata
allora
L [ f (t) ] = F1(s) ; L [ f2(t) ] = F2(s)
L [ c f (t) + c2 f2(t) ] = c1 F1(s) + c2 F2(s)
ove
c1 e c2 sono due costanti reali o complesse
2. Trasformate elementari
3. Proprietà
1
4. Applicazione ai
componenti elettrici
1 1
5. Antitrasformazione
Se
La proprietà di linearità permette di applicare il metodo delle trasformata di
Laplace a tutti i circuiti (e sistemi) lineari
Sono circuiti lineari quelli contenenti componenti nei quali vi è una relazione
lineare fra le grandezze elettriche. Tutti i componenti considerati in questo
corso sono lineari
Altri componenti (come il diodo) sono non lineari e allora il metodo della
trasformata di Laplace non può essere applicato
15
M. Salerno
Laplace
Trasformata di Laplace: proprietà
Trasformata di Laplace
Linearità
Derivazione
1. Definizione
Tor Vergata
allora
f (t)]]==F(s)
F1(s) ; L [ f2(t) ] = F2(s)
L [ f(t)
-) + c F (s)
L [ dc f(t)
] =–c1f F(01(s)
f (t)/ dt
+ c]2=f2s(t)F(s)
2 2
ove
fc1(0e -c)2 èsono
il valore
due costanti
di f(t) per
realit o= complesse
0-
2. Trasformate elementari
3. Proprietà
1
4. Applicazione ai
componenti elettrici
1 1
5. Antitrasformazione
Se
La proprietà di linearità
derivazione
permette
permette
di applicare
di sostituire
il metodo
operazioni
delledifferenziali
trasformata
neldi
dominio
Laplace del
a tutti
tempo
i circuiti
con operazioni
(e sistemi)algebriche
lineari nel dominio di s
Sono
lineari
quelli contenenti
componenti
nei qualidiviLaplace
è una relazione
Se
f(t)circuiti
presenta
discontinuità,
la derivata
e la trasformata
devono
lineare
fra
le
grandezze
elettriche.
Tutti
i
componenti
considerati
in
questo
essere applicate nel senso delle distribuzioni
corso sono lineari
per tenere
di eventuali
discontinuità
L’istante
0 - è considerato
Altri
componenti
(come il diodo)
sonoconto
non lineari
e allora
il metodo della
nell’origine. di
Nell’ambito
delle
funzioni
si considera semplicemente f(0)
trasformata
Laplace non
può
essere applicato
15
M. Salerno
Laplace
Trasformata di Laplace: proprietà
Trasformata di Laplace
Linearità
Derivazione
Traslazione
1. Definizione
Tor Vergata
f (t)]]==F(s)
F1(s) ; L [ f2(t) ] = F2(s)
L [ f(t)
-) + c F (s)
-sT–c f F
]
f –(t)/T)dt
+]c]=2=fF(s)
s
(t)
F(s)
=
(0
(s)
e
L[[dcf(tf(t)
allora
allora L
2
1 1
2 2
2. Trasformate elementari
3. Proprietà
1
4. Applicazione ai
componenti elettrici
1 1
5. Antitrasformazione
Se
ove
ove
(te --c)T)
è
la
f(t)
traslata
dell’intervallo
T
fcf1(0
è
sono
il
valore
due
costanti
di
f(t)
per
reali
t
o
=
complesse
0
2
La proprietà di linearità
derivazione
permette
permette
di applicare
di sostituire
il metodo
operazioni
delledifferenziali
trasformata
neldi
La proprietà di traslazione è molto utile per tenere conto di ritardi nella
dominio
Laplace del
a tutti
tempo
i circuiti
con operazioni
(e sistemi)algebriche
lineari nel dominio di s
trasmissione di segnali elettrici (è poco usata nei circuiti elementari)
Sono
lineari
quelli contenenti
componenti
nei qualidiviLaplace
è una relazione
Se
f(t)circuiti
presenta
discontinuità,
la derivata
e la trasformata
devono
Molte fra
altre
proprietà
della
trasformata
di
Laplace sono
omesse perché
non
lineare
le
grandezze
elettriche.
Tutti
i
componenti
considerati
in
questo
essere applicate nel senso delle distribuzioni
assolutamente
essenziali alla trattazione
corso
sono lineari
per tenere
di eventuali
discontinuità
L’istante
0 - è considerato
Altri
componenti
(come il diodo)
sonoconto
non lineari
e allora
il metodo della
nell’origine. di
Nell’ambito
delle
funzioni
si considera semplicemente f(0)
trasformata
Laplace non
può
essere applicato
15
M. Salerno
Tor Vergata
Laplace
Proprietà di derivazione: esempi
Verifica proprietà di derivazione
f(t) = e t u-1(t)
f(0-) = 0
F(s) = L[f(t)] = 1/ (s-1)
dalla proprietà di derivazione
L[df(t)/dt] = sF(s) – f(0-)
= s/(s-1)
verifica
16
M. Salerno
Tor Vergata
Laplace
16
Proprietà di derivazione: esempi
Verifica proprietà di derivazione
f(t) = e t u-1(t)
f(0-) = 0
F(s) = L[f(t)] = 1/ (s-1)
dalla proprietà di derivazione
L[df(t)/dt] = sF(s) – f(0-)
= s/(s-1)
verifica
df(t)/dt = e t u-1(t) + e t u0(t)
= e t u-1(t) + u0(t)
dalla proprietà di linearità
L[df(t)/dt] = 1/(s-1)
= s/(s-1)
+1
M. Salerno
Tor Vergata
Laplace
16
Proprietà di derivazione: esempi
Verifica proprietà di derivazione
f(t) = e t u-1(t)
f(0-) = 0
F(s) = L[f(t)] = 1/ (s-1)
dalla proprietà di derivazione
L[df(t)/dt] = sF(s) – f(0-)
verifica
df(t)/dt = e t u-1(t) + e t u0(t)
= e t u-1(t) + u0(t)
dalla proprietà di linearità
L[df(t)/dt] = 1/(s-1)
= s/(s-1)
+1
= s/(s-1)
Trasformate delle distribuzioni successive
uk(0-) = 0 , k = 0, 1, 2, …
uk(t) = d uk-1(t) / dt , k = 1, 2, …
L[u0(t)] = 1
L[uk(t)] = s L[uk-1(t)]
L[uk(t)] = sk
M. Salerno
Proprietà di linearità: esempi
Trasformata della funzione
sinusoidale
nel campo complesso
f(t) = F cos (ωt + ϕ ) u-1(t)
f(t) = ½ (F e jωt + F* e -jωt ) u-1(t)
ove F = Fe jϕ è il fasore di f(t)
dalle trasformate elementari
L[e + jωt u-1(t)] = 1/(s
+
Tor Vergata
Laplace
jω)
dalla proprietà di linearità
F(s) = L[f(t)] = ½ [F /(s - jω) + F*/(s + jω) ]
L’espressione trovata può essere considerata soddisfacente in vari casi
Tuttavia è possibile sviluppare ulteriormente i calcoli
17
M. Salerno
Proprietà di linearità: esempi
Trasformata della funzione
sinusoidale
nel campo complesso
f(t) = F cos (ωt + ϕ ) u-1(t)
f(t) = ½ (F e jωt + F* e -jωt ) u-1(t)
ove F = Fe jϕ è il fasore di f(t)
dalle
F(s)trasformate
= ½ [F /(selementari
- jω) + F*/(s + jω) ];
L[
] = 1/(s
+ jωϕ
tu
F = Fe jϕ = F (cos ϕ + ej sin
) -1(t)
+
Tor Vergata
Laplace
jω)
dalla proprietà di linearità
F(s) = ½ F[(cos ϕ + j sin ϕ ) /(s - jω) + (cos ϕ - j sin ϕ ) /(s + jω) ] =
F(s) = L[f(t)] = ½ [F /(s - jω) + F*/(s + jω) ]
= ½F[(cos ϕ + j sin ϕ )(s + jω) + (cos ϕ - j sin ϕ )(s - jω) ]/(s2 + ω2) =
L’espressione trovata può essere considerata soddisfacente in vari casi
2 + ω2)
=
F
(s
cos
ϕ
ω
sin
ϕ
)
/(s
Tuttavia è possibile sviluppare ulteriormente i calcoli
17
M. Salerno
Tor Vergata
Laplace
17
Proprietà di linearità: esempi
Trasformata della funzione
sinusoidale
nel campo complesso
f(t) = F cos (ωt + ϕ ) u-1(t)
f(t) = ½ (F e jωt + F* e -jωt ) u-1(t)
ove F = Fe jϕ è il fasore di f(t)
dalle
F(s)trasformate
= ½ [F /(selementari
- jω) + F*/(s + jω) ];
F(s) = ½ [F /(s - jω) + F*/(s + jω) ]
+ jωϕ
tu
1/(s
jω2) + ω2)
F = Fe jϕ = F (cos=L[
ϕF
+ ej(s
sin
)ϕ
cos
- ]ω=sin
ϕ ) /(s
-1(t)
+
dalla
di linearità
F(s)proprietà
è una funzione
razionale (rapporto fra polinomi) a coefficienti reali
F(s) = ½ F[(cos ϕ + j sin ϕ ) /(s - jω) + (cos ϕ - j sin ϕ ) /(s + jω) ] =
L[ ]
½ [Freali
/(sper
- jsωreale
) + F*/(s
F(s) è detta razionaleF(s)
reale, =
perché f(t)
assume=valori
+ jω) ]
= ½F[(cos ϕ + j sin ϕ )(s + jω) + (cos ϕ - j sin ϕ )(s - jω) ]/(s2 + ω2) =
F(s) è anche espressa
come
somma
di due funzioni
complesse
coniugate,
per s reale
L’espressione
trovata può
essere
considerata
soddisfacente
in vari
casi
2 + ω2)
=
F
(s
cos
ϕ
ω
sin
ϕ
)
/(s
Tuttavia
è possibile
ulteriormente
i calcoli possono essere semplificati
Sulla base
di questesviluppare
osservazioni,
i calcoli precedenti
M. Salerno
Tor Vergata
Laplace
Proprietà di linearità: esempi
Trasformata della funzione
sinusoidale
f(t) = F cos (ωt + ϕ ) u-1(t)
nel campo complesso
ωt ]eujωt(t)
f(t) = Re[
F½
e j(F
, con
Fe
f(t) =
e -jωFt ) =u-1
(t)jϕ
-1 + F*
ove F = Fe jϕ è il fasore di f(t)
F(s) = Re[ F /(s - jω) ]
dalle
F(s)trasformate
= ½ [FF(s)
/(selementari
- j=
ω)½
+ F*/(s
+ -jωjω
) ];) + F*/(s + jω) ]
[F
/(s
ove l’operatore Re[.] è applicato considerando s reale
+ jωϕ
tu
1/(s
jω2) + ω2)
F = Fe jϕ = F (cos=L[
ϕF
+ ej(s
sin
)ϕ
cos
- ]ω=sin
ϕ ) /(s
-1(t)
F(s) = F Re[(cos ϕ + j sin ϕ ) /(s - jω) ] =
dalla proprietà di linearità
+
F(s) è una funzione razionale (rapporto fra polinomi) a coefficienti reali
F(s) = ½ F[(cos ϕ + j sin ϕ ) /(s - jω) + (cos ϕ - j sin ϕ ) /(s + jω)2] = 2
=
f(t)ϕ += j½sin
[Fϕ/(s
- j+ω)jω+)F*/(s
=F(s)
F Re[(cos
) (s
] /(s + jωω) ]
L[ ]
F(s) è detta razionale reale, perché assume valori reali per s reale
= ½F[(cos ϕ + j sin ϕ )(s + jω) + (cos ϕ - j sin ϕ )(s - jω) ]/(s2 + ω2) =
sufficiente
i termini
reali del
prodotto)
F(s) è anche espressa(ècome
somma calcolare
di due funzioni
complesse
coniugate,
per s reale
L’espressione trovata può essere considerata soddisfacente in vari casi
2 + ω2)
=
F
(s
cos
ϕ
ω
sin
ϕ
)
/(s
2 + ω2)
F(s)
=
F
(s
cos
ϕ
ω
sin
ϕ ) /(s
Tuttavia
è possibile
ulteriormente
i calcoli
Sulla base
di questesviluppare
osservazioni,
i calcoli precedenti
possono
essere semplificati
17
M. Salerno
Tor Vergata
Laplace
17
Proprietà di linearità: esempi
Trasformata della funzione
sinusoidale
Notazione
f(t) = F cos (ωt + ϕ ) u-1(t)
nel campo complesso
j(F
ωt ]euha
jωt(t)
f(t)La
= lettera
Re[
F½
e “F”
, con
Fe
f(t) =
F*
e -jωFt ) =u-1
(t)jϕ
vari
significati:
-1 +
ove F = Fe jϕ è il fasore di f(t)
(minuscolo)
F(s) =f Re[
F /(s - jωè) ]la funzione del tempo f(t)
dalle
F(s)trasformate
= ½ [FF(s)
/(selementari
- j=
ω)½
+ F*/(s
+ -jωjω
) ];) + F*/(s + jω) ]
[F
/(s
ove
Re[.]è èl’ampiezza
applicato considerando
F l’operatore
(maiuscolo)
(modulo)s reale
+ jωϕ
tu
1/(s
jω2) + ω2)
F = Fe jϕ = F (cos=L[
ϕF
+ ej(s
sin
)ϕ
cos
- ]ω=sin
ϕ ) /(s
-1(t)
F
(maiuscolo
e+sottolineato)
èjωil) fasore
F(s)
=
F
Re[(cos
ϕ
j
sin
ϕ
)
/(s
]=
dalla proprietà di linearità
+
F(s) è una funzione razionale (rapporto fra polinomi) a coefficienti reali
+ j sin
ϕ ) /(s - jω) +è(cos
ϕ - j sin ϕ ) /(s +dijωLaplace
)2] = 2
F(s) = ½ F[(cos ϕF(s)
(maiuscolo)
la trasformata
L[ ]
=perché f(t)
[Freali
- j+
)jω+)F*/(s
F Re[(cos
ϕ +=valori
j½sin
ϕ/(s
) per
(s
] /(s
F(s) è detta razionale=F(s)
reale,
assume
sωreale
+ jωω) ]
= ½F[(cos ϕ + j sin ϕ )(s + jω) + (cos ϕ - j sin ϕ )(s - jω) ]/(s2 + ω2) =
sufficiente
i termini
reali del
prodotto)
F(s) è anche espressa(ècome
somma calcolare
di due funzioni
complesse
coniugate,
per s reale
L’espressione trovata può essere considerata soddisfacente in vari casi
2 + ω2)
=
F
(s
cos
ϕ
ω
sin
ϕ
)
/(s
2 + ω2)
F(s)
=
F
(s
cos
ϕ
ω
sin
ϕ ) /(s
Tuttavia
è possibile
ulteriormente
i calcoli
Sulla base
di questesviluppare
osservazioni,
i calcoli precedenti
possono
essere semplificati
M. Salerno
Tor Vergata
Laplace
18
Proprietà di traslazione: esempi
Trasformata della funzione
f(t) = A [ u-1(t) - u-1(t-T)]
f(t)
A
dalle proprietà di traslazione
e di linearità :
F(s) = A (1 - e-sT)/s
T
t
M. Salerno
Tor Vergata
Laplace
18
Proprietà di traslazione: esempi
Trasformata della funzione
∞
f(t)
f(t) = A [ u-1(t) - uk -1(t-T)]
f(t) = A Σ [(-1) u-1(t – k T)]
A
k=0 di traslazione
dalle proprietà
e di linearità :
La forma d’onda è costituita
dalla somma di infiniti gradini
-sT
F(s) = A (1 - e )/s
alternativamente positivi e negativi, di ampiezza A e traslati
dell’intervallo di tempo T l’uno rispetto all’altro
T
t
L’impulso di ampiezza A e durata T può essere replicato indefinitamente,
ottenendo un’onda quadra. Tale funzione è nulla per t < 0
f(t)
A
T
2T
3T
4T
5T
t
M. Salerno
Tor Vergata
Laplace
18
Proprietà di traslazione: esempi
Trasformata della funzione
∞
f(t)
f(t) = A [ u-1(t) - uk -1(t-T)]
f(t) = A Σ [(-1) u-1(t – k T)]
A
k=0 di traslazione
dalle proprietà
e diproprietà
linearità di
: traslazione e linearità :
Dalle
La forma d’onda è costituita
dalla somma di infiniti gradini T
-sT
t
F(s) = A (1 - ∞
e )/se negativi, di ampiezza A e traslati
alternativamente positivi
Si ricordi che
k –k sT ]
F(s) = (A/s)
dell’intervallo
di tempo[(-1)
T l’uno erispetto all’altro
1
k=0
=
1
+
x
L’impulso di ampiezza
A e durata T può essere replicato indefinitamente,
A
2 – x 3 + x4 - …
= un’onda quadra.
ottenendo
Tale
funzione
è
nulla
per
t
<
0
=
1
–
x
+
x
–
sT
s(1+e
)
Σ
f(t)
A
T
2T
3T
4T
5T
t
M. Salerno
Tor Vergata
Laplace
Bipoli nel dominio di Laplace
Trasformata di Laplace
1. Definizione
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
componenti elettrici
5. Antitrasformazione
19
M. Salerno
Tor Vergata
Laplace
19
Bipoli nel dominio di Laplace
Trasformata di Laplace
Trasformate
di Laplace
1. Definizione
di2.tensione
e corrente
Trasformate elementari
3. Proprietà
4. Applicazione ai
= V(s)
componenti elettrici
5. Antitrasformazione
L [ v(t) ]
;
+
i(t)
L [ i(t) ] = I(s)
Si definisce un istante iniziale, tipicamente t = 0
All’istante t = 0- sono assegnate le condizioni iniziali
tensione: v(t) in Volt (V)
; V(s) in Volt.sec (V.s)
corrente: i(t) in Ampère (A) ; I(s) in Ampère.sec (A.s)
Il bipolo indicato si dice nel dominio del tempo
v(t)
bipolo nel
dominio del tempo
M. Salerno
Tor Vergata
Laplace
19
Bipoli nel dominio di Laplace
Trasformata di Laplace
Trasformate
di Laplace
1. Definizione
di2.tensione
e corrente
Trasformate elementari
3. Proprietà
4. Applicazione ai
= V(s)
componenti elettrici
5. Antitrasformazione
L [ v(t) ]
;
+
i(t)
I(s)
L [ i(t) ] = I(s)
Si definisce un istante iniziale, tipicamente t = 0
All’istante t = 0- sono assegnate le condizioni iniziali
tensione: v(t) in Volt (V)
; V(s) in Volt.sec (V.s)
corrente: i(t) in Ampère (A) ; I(s) in Ampère.sec (A.s)
V(s)
v(t)
bipolo nel
dominio
dominio di
delLaplace
tempo
Il bipolo indicato si dice nel dominio del tempo
Indicando le trasformate invece delle grandezze nel tempo si ottiene
il bipolo nel dominio di Laplace
M. Salerno
Tor Vergata
Laplace
19
Bipoli nel dominio di Laplace
Trasformata di Laplace
Trasformate
di Laplace
1. Definizione
di2.tensione
e corrente
Trasformate elementari
3. Proprietà
4. Applicazione ai
= V(s)
componenti elettrici
5. Antitrasformazione
L [ v(t) ]
;
+
i(t)
I(s)
L [ i(t) ] = I(s)
Si definisce un istante iniziale, tipicamente t = 0
All’istante t = 0- sono assegnate le condizioni iniziali
tensione: v(t) in Volt (V)
; V(s) in Volt.sec (V.s)
corrente: i(t) in Ampère (A) ; I(s) in Ampère.sec (A.s)
V(s)
v(t)
bipolo nel
dominio
dominio di
delLaplace
tempo
Il
si dice
nel dominio
del tempo
Il bipolo
bipolo indicato
nel dominio
di Laplace
è utilizzato
solo a scopi di calcolo
Indicando le trasformate invece delle grandezze nel tempo si ottiene
Nel
bipolo
le grandezze
elettriche sono sempre funzioni del tempo
il bipolo
nelreale
dominio
di Laplace
M. Salerno
Tor Vergata
Laplace
Resistore
Nel dominio del tempo
Nel dominio
di Laplace
+
v(t) = R i(t)
V(s) = R I(s)
v(t) = R i(t)
L [ v(t) ] = L [ R i(t) ]
per la linearità
L [ v(t) ] = R L [i(t) ]
V(s) = R I(s)
R
v(t) = R i(t)
+
R
V(s) = R I(s)
20
M. Salerno
Tor Vergata
Laplace
+
Induttore
Nel dominio del tempo v(t) = L d i(t) / d t
Nel dominio
-)
V(s)
=
s
L
I(s)
–
L
i(0
di Laplace
i(0 -) condizione iniziale
v(t) = L d i(t) / d t
L [ v(t) ] = L [L d i(t) / d t ]
per le proprietà di linearità e di derivazione
L [ v(t) ] = L [s L [ i(t) ] - i(0 -)]
V(s) = s L I(s) – L i(0 -)
21
L
v(t) = L d i(t) / d t
Caso particolare
condizione iniziale nulla:
i(0 -) = 0
V(s) = s L I(s)
+
sL
V(s) = sL I(s)
sL
impedenza
M. Salerno
Tor Vergata
Laplace
+
Induttore
Nel dominio del tempo v(t) = L d i(t) / d t
Nel dominio
-)
V(s)
=
s
L
I(s)
–
L
i(0
di Laplace
i(0 -) condizione iniziale
caso generale
i(0L-)d=/i(t)
0 /dt
v(t): =
-)
sL
L
i(0
LI(s)[ v(t) ] = L [L d i(t) / +
dt]
per le proprietà di linearità e di derivazione
+
V(s)
-)]
L
[
L
[
v(t)
]
=
L
s
[
i(t)
]
i(0
Li(0 ) tensione impressa del generatore,
con segno positivo a destra
-)
= s L I(s)elettriche
– L i(0esterne
V(s),V(s)
I(s) grandezze
21
L
v(t) = L d i(t) / d t
Caso particolare
condizione iniziale nulla:
i(0 -) = 0
V(s) = s L I(s)
+
sL
V(s) = sL I(s)
sL
impedenza
M. Salerno
Tor Vergata
Laplace
Induttore
+
a
Nel dominio del tempo v(t) = L d i(t) / d t
Nel dominio
-)
V(s)
=
s
L
I(s)
–
L
i(0
di Laplace
i(0 -) condizione iniziale
caso generale
i(0L-)d=/i(t)
0 /dt
v(t): =
A
-)
sL
L
i(0
LI(s)[ v(t) ] = L [L d i(t) / +
dt]
B
per le proprietà di linearità e di derivazione
+
V(s)
-)]
L
[
L
[
v(t)
]
=
L
s
[
i(t)
]
i(0
Li(0 ) tensione impressa del generatore,
Equivalenza:
dominio
tempo a: bipolo
con
segnodel
positivo
destra ab
-)
dominio
di =
Laplace:
bipolo
completo
V(s)
s L I(s)
– LABi(0
V(s),
I(s)
grandezze
elettriche
esterne
21
L
v(t) = L d i(t) / d t
Caso particolare
condizione iniziale nulla:
i(0 -) = 0
V(s) = s L I(s)
+
sL
V(s) = sL I(s)
sL
impedenza
b
M. Salerno
Tor Vergata
Laplace
22
Induttore: schemi equivalenti
Dominio del tempo
Dominio di Laplace
A
I(s)
+
sL
L i(0 -)
+
B
V(s)
I(s)
+
L
i(t)
b
i(0 -)
Equivalenza fra generatori
i(0 -)/s
A
a
+ v(t)
+
v
B
V(s)
La corrente impressa dal generatore di corrente
è pari a L i(0 -) / sL = i(0 -) / s
R
g
vg / R = ig
ig
R
l’impedenza sL svolge lo stesso
ruolo della resistenza R
M. Salerno
Tor Vergata
Laplace
22
Induttore: schemi equivalenti
Dominio del tempo
Dominio di
delLaplace
tempo
A
I(s)
i(t)
+
sL
L
L Li(0
i(0-) -u) 0(t)
+
B
V(s)
I(s)
i(t)
+
V(s)
v(t)
L
i(t)
b
i(0 -)
Equivalenza
Si
ricordi chefra generatori
-) -u (t)
i(0i(0
)/s
-1
A
a
+ v(t)
L
+
v
R
-1
L [L i(0-)] = L i(0-)u0(t)
B
La corrente impressa dal generatore di corrente
In questi schemi equivalenti, gli induttori sono
è pari a L i(0 -) / sL = i(0 -) / s
considerati con condizioni iniziali nulle
g
L-1[i(0-)/s] = i(0-v) u-1/ (t)R = i
g
espressioni permettono
igQueste
R nel dominio
di interpretare
del tempo gli schemi
equivalenti
dell’induttore
l’impedenza
sL svolge lo stesso
ruolo della resistenza R
g
M. Salerno
Tor Vergata
Laplace
23
+
Condensatore
Nel dominio del tempo i(t) = C d v(t) / d t
C
i(t) = C d v(t) / d t
Nel dominio
Caso particolare
di Laplace I(s) = s C V(s) – C v(0 ) condizione iniziale nulla:
v(0 -) condizione iniziale
v(0 -) = 0
i(t) = C d v(t) / d t
L [ i(t) ] = L [C d v(t) / d t ]
per le proprietà di linearità e di derivazione
L [ i(t) ] = C [s L [ v(t) ] - v(0 -)]
I(s) = s C V(s) – C v(0
-)
+
1/sC
I(s)
s CV(s)
V(s)
I(s) ==sC
sC
1/sC
ammettenza
impedenza
M. Salerno
Tor Vergata
Condensatore
Nel dominio del tempo i(t) = C d v(t) / d t
Laplace
+
23
C
i(t) = C d v(t) / d t
Nel dominio
Caso particolare
di Laplace I(s) = s C V(s) – C v(0 ) condizione iniziale nulla:
v(0 -) condizione iniziale
v(0 -) = 0
caso generale
/0 /dt
i(t): =v(0
C -d) =
v(t)
1/sC
+
-)
C
v(0
L [ i(t) ] = L [C d v(t) / d t ]
I(s)
s CV(s)
V(s)
I(s) ==sC
per le proprietà di linearità e di derivazione
I(s)
s C ammettenza
L [ i(t) ] = C [s L1/sC
[ v(t) ] - v(0 -)]
V(s)
+
1/sC impedenza
s C V(s)elettriche
– C v(0esterne
)
V(s),I(s)
I(s)=grandezze
M. Salerno
Tor Vergata
Condensatore
Nel dominio del tempo i(t) = C d v(t) / d t
Laplace
a
+
23
C
i(t) = C d v(t) / d t
Nel dominio
Caso particolare
di Laplace I(s) = s C V(s) – C v(0 ) condizione iniziale nulla:
v(0 -) condizione iniziale
v(0 -) = 0
caso generale
/0 /dt
i(t): =v(0
C -d) =
v(t)
1/sC
+
-)
C
v(0
L [ i(t) ] = L [C d v(t) / d t ]
I(s)
s CV(s)
V(s)
I(s) ==sC
per le proprietà di linearità e di derivazione
I(s)
A
B
s C ammettenza
L [ i(t) ] = C [s L1/sC
[ v(t) ] - v(0 )]
V(s)
+
1/sC impedenza
I(s)
s C V(s)
–C
)
V(s),
I(s)
elettriche
esterne
bipolo
ab=grandezze
bipolo
ABv(0
completo
b
M. Salerno
Tor Vergata
Laplace
24
Condensatore: schemi equivalenti
Dominio del tempo
Dominio di Laplace
C v(0 -)
+ v(t)
a
A
I(s)
+
A
I(s)
+
1/sC
V(s)
1/sC
i(t)
+
b
v(0 -)
B
Equivalenza fra generatori
+
v
v(0 -)/s
+
C
R
g
B
V(s)
La tensione impressa dal generatore di tensione
è pari a C v(0 -) / sC = v(0 -) / s
vg= R ig
ig
R
l’impedenza 1/sC svolge lo
stesso ruolo della resistenza R
M. Salerno
Tor Vergata
Laplace
24
Condensatore: schemi equivalenti
Dominio del tempo
Dominio di
delLaplace
tempo
-) u-) (t)
C v(0
C v(0
0
A
I(s)
i(t)
+
A
I(s)
i(t)
+
1/sC
C
V(s)
v(t)
C
1/sC
a
i(t)
b
+
v(0 -)
B
Equivalenza
Si
ricordi chefra generatori
+
v
R-1
L [C v(0 )] = C v(0-)u0(t)
-) -u)/s(t)
v(0v(0
-1
+
+ v(t)
C
g
B
V(s)
v(t)
Intensione
questi schemi
equivalenti,
i condensatori
La
impressa
dal generatore
di tensione
è sono
pari aconsiderati
C v(0 -) /con
sC condizioni
= v(0 -) / s iniziali nulle
L-1[v(0-)/s] = v(0-v) u=-1(t)R i
g
g
espressioni permettono
igQueste
R nel dominio
di interpretare
del tempo gli schemi
equivalenti
del1/sC
condensatore
l’impedenza
svolge lo
stesso ruolo della resistenza R
M. Salerno
Tor Vergata
Laplace
25
Esempio: circuito RC
circuito nel
dominio di s
a
C +
t=0
v0
i(t)
R
v0 /s
A
+
I(s)
R
1/sC
b v0 condizione iniziale
B
Il bipolo completo fra i morsetti AB è l’equivalente del condensatore
nel dominio del tempo, inclusa la condizione iniziale
analisi nel
dominio di s
I(s) (R + 1/sC) = v0 /s
I(s) (sRC + 1)/C = v0
I(s) = v0 C/(sRC + 1)
I(s) = (v0 /R)/(s + 1/RC)
antitrasformazione
i(t) = L-1[I(s)] =
= L-1[(v0 /R)/(s + 1/RC)] =
= (v0 /R)
e –t /RC u-1 (t)
M. Salerno
Tor Vergata
26
Esempio: circuito RCC
t=0
a
C
Laplace
+
+
C1
R
v0
b
condizioni iniziali
condensatore C : v0
condensatore C1 : 0
v(t)
dominio di t
V(s) (sC + s C1 + 1/R) = C v0
V(s) = C v0 / (sC + s C1 + 1/R)
C
C + C1 s +
C v0
1
1
R(C + C1 )
1/sC1
R
1/sC
il condensatore C equivale
all’intero bipolo a sinistra
dei morsetti AB
analisi nel dominio di s
V(s) = v0
A + V(s)
B
dominio di s
antitrasformazione
v(t) = L-1[V(s)]
da L-1[1/(s+a)] = e-at u-1(t)
e dalla proprietà di linearità
v(t) = v0
C e-t/R (C + C1) u (t)
-1
C + C1
M. Salerno
Tor Vergata
26
Esempio: circuito RCC
t=0
a
C
Laplace
+
+
C1
R
v0
b
condizioni iniziali
condensatore C : v0
condensatore C1 : 0
v(t)
dominio di t
C
-t/R(C + C1)
u-1 (t)
1/sC
B
dominio di s
La costante
di tempo è : τ = R (C + C1 ).
antitrasformazione
-1
1
1
R(C + C1 )
R
L
V(s) = C v0 / (sC + s C1 + 1/R)
C
C + C1 s +
1/sC1
C +v(t)
C1 condensatore
= -1[V(s)parallelo
]
(condensatore visto dalla resistenza R dopo
la chiusura dell’interruttore)
da L-1[1/(s+a)] = e-at u (t)
V(s) (sC + s C1 + 1/R) = C v0
V(s) = v0
C v0
il condensatore C equivale
all’intero bipolo a sinistra
dei morsetti AB
v(t) = v
e
analisivnel
(t) dominio di0 Cs + C1
v0 C/(C+C1 )
A + V(s)
e dalla proprietà di linearità
C
C1
C+C
t
1
C
-t/R
(C
+
C1) u (t)
v(t) = v0
e
-1
C + C1
M. Salerno
26
Esempio: circuito RCC
Tor Vergata
vc(t)
t=0
a
C
Laplace
+
+
C1
condizioni iniziali
condensatore C : v0
condensatore C1 : 0
v(t)
R
v0
b
vc(t)
=
v(t)
= di
v0vs0 |t < 0 e
analisivnel
C + C1
(t) dominio
C
-t/R(C + C1)
u-1 (t)
C e-t/R(C + C1 ) |
t>0
CCv+0 C1
vc(t) = v0
V(s) (sC + s Cv01 + 1/R) =
V(s) = C v0 / (sC + s C1 + 1/R)
V(s) = v0
C
C + C1 s +
C v0
R
B
dominio di s
La costante
di tempo è : τ = R (C + C1 ).
antitrasformazione
L
C +v(t)
C1 condensatore
= -1[V(s)parallelo
]
(condensatore visto dalla resistenza R dopo
la chiusura dell’interruttore)
da L-1[1/(s+a)] = e-at u (t)
-1
1
1
R(C + C1 )
1/sC1
1/sC
il condensatore C equivale
all’intero bipolo a sinistra
dei morsetti AB
dominio di t
v0 C/(C+C1 )
A + V(s)
e dalla proprietà di linearità
C
C1
C+C
t
1
C
-t/R
(C
+
C1) u (t)
v(t) = v0
e
-1
C + C1
M. Salerno
26
Esempio: circuito RCC
Tor Vergata
vc(t)
t=0
a
C
Laplace
+
+
C1
condizioni iniziali
condensatore C : v0
condensatore C1 : 0
v(t)
R
v0
b
vc(t)
=
v(t)
= di
v0vs0 |t < 0 e
analisivnel
C + C1
(t) dominio
C
-t/R(C + C1)
u-1 (t)
C e-t/R(C + C1 ) |
t>0
CCv+0 C1
vc(t) = v0
V(s) (sC + s Cv01 + 1/R) =
V(s) = C v0 / (sC + s C1 + 1/R)
V(s) = v0
C
C + C1 s +
C v0
1
1
R(C + C1 )
t
1/sC1
R
1/sC
il condensatore C equivale
all’intero bipolo a sinistra
dei morsetti AB
dominio di t
v0 C/(C+C1 )
A + V(s)
B
dominio di s
Bilancio
energetico
La costante
di tempo è : τ = R (C + C1 ).
antitrasformazione
t<0:
E0 = ½ C vo2
-1[V(s)parallelo
C +v(t)
C1 condensatore
=
][v C/(C+C )] 2 +
+
t(condensatore
=0 :
Evisto
=
½
C
1
dalla oresistenza1 R dopo
+
½
C1 [vo C/(C+C1 )] 2 =
la chiusura dell’interruttore)
-1
da L [1/(s+a)]
= e-at u-11 (t)
)] < E0
= ½ C vo2[C/(C+C
e dalla proprietà di linearità
C perduta
C1
Energia
C+C1
EPv(t)
= E0=- Ev1 = ½C
C vo2 [1
)] =(t)
-t/RC/(C+C
(C + C1)1u
e
0
2 [C C /(C+C )] -1
=C½+voC
1
1
1
L
M. Salerno
vc(t)
t=0
a
+
+
C1
v(t)
R
v0
b
26
Esempio: circuito RCC
Tor Vergata
C
Laplace
dominio di t
condizioni iniziali
condensatore C : v0
condensatore C1 : 0
A + V(s)
C v0
C
-t/R(C + C1)
vc(t) = v0 C e-t/R(C + C1 ) |t > 0
condensatore serie
V(s)
(sC + s Cv01 + 1/R)
C = CCv+0 C1
C1
(condensatore visto
dall’interruttore)
V(s)
= C v0 / (sC + s C1 + 1/R)
1)
E v0èC/(C+C
pari all’energia
immagazzinata dal condensatore
C
1
V(s)serie,
= v0carico alla tensione iniziale v0
1
C + C1 s +
EP è assorbita dall’interruttore,
per t=0
R(C + C1 )
P
E1 è assorbita dal resistore, per t>0
t
R
1/sC
il condensatore C equivale
all’intero bipolo a sinistra
dei morsetti AB
vc(t)
=
v(t)
= di
v0vs0 |t < 0 e
u (t)
analisivnel
dominio
C + C1 C C1 /(C+C-11 )
(t)
C C1 /(C+C
)
1
1/sC1
B
dominio di s
Bilancio
energetico
La costante
di tempo è : τ = R (C + C1 ).
antitrasformazione
t<0:
E0 = ½ C vo2
-1[V(s)parallelo
C +v(t)
C1 condensatore
=
][v C/(C+C )] 2 +
+
t(condensatore
=0 :
Evisto
=
½
C
1
dalla oresistenza1 R dopo
+
½
C1 [vo C/(C+C1 )] 2 =
la chiusura dell’interruttore)
-1
da L [1/(s+a)]
= e-at u-11 (t)
)] < E0
= ½ C vo2[C/(C+C
e dalla proprietà di linearità
C perduta
C1
Energia
C+C1
EPv(t)
= E0=- Ev1 = ½C
C vo2 [1
)] =(t)
-t/RC/(C+C
(C + C1)1u
e
0
2 [C C /(C+C )] -1
=C½+voC
1
1
1
L
M. Salerno
Tor Vergata
Laplace
27
Esempio: circuito RL
t=0
sL
L
+
+
i(t)
R
v0
i(t) = 0 | t < 0
I(s)
v0 /s
dominio di t
analisi nel
dominio di s I(s) (sL + R)
I(s) = [v0 / L]/[s (s + R/L)]
= v0 /s
dominio di s
antitrasformazione
i(t) = L-1[I(s)] =
L-1[(v0 / R) / s - (v0 / R) / (s + R/L)]
Per antitrasformare I(s) si pone
=
I(s) = A/s + B /(s + R/L)
Per la proprietà di linearità
Risulta
A (s + R/L)] + B s = v0 / L
A = v0 / R
; B = - v0 / R
R
i(t) = (v0 /R) (1 - e – t L/R ) u-1 (t)
M. Salerno
Tor Vergata
Laplace
27
Esempio: circuito RL
t=0
sL
L
+
+
i(t)
R
v0
i(t) = 0 | t < 0
I(s)
v0 /s
dominio di t
analisi nel
i(t) = (v0 /R) (1 - e – t L/R ) u-1 (t)
i (t) di s I(s) (sL + R) = v0 /s
dominio
Costante di tempo τ = R / L
I(s) = [v0 / L]/[s (s + R/L)]
v0 /R
dominio di s
antitrasformazione
i(t) = L-1[I(s)] =
L-1[(v0 / R) / s - (v0 / R) / (s + R/L)]
Per antitrasformare I(s) si pone
=
I(s) = A/s + B /(s + R/L)
Per la proprietà di linearità
Risulta
A (s + R/L)] + B s = v0 / L
t
A = v0 / R ; B = - v0 / R
R
i(t) = (v0 /R) (1 - e – t L/R ) u-1 (t)
M. Salerno
Tor Vergata
Antitrasformazione
Trasformata di Laplace
1. Definizione
2. Trasformate elementari
3. Proprietà
4. Applicazione ai
componenti elettrici
5. Antitrasformazione
Laplace
28
M. Salerno
Tor Vergata
Laplace
Antitrasformazione
Trasformata di Laplace
Metodo delle Trasformata di Laplace
1. Definizione
1.2. Trasformate
Dal circuitoelementari
nel dominio del tempo determinare il circuito nel
dominio di Laplace
3. Proprietà
4. Applicazione
ai
Per i componenti
R, L, C, utilizzare i circuiti equivalenti
componenti elettrici
Per i generatori, calcolare la trasformata delle grandezze impresse
5. Antitrasformazione
2. Risolvere il circuito nel dominio di Laplace
Tutte le grandezze elettriche (tensioni e correnti) sono funzioni di s
3. Antitrasformare le grandezze di interesse per ottenere le relative
funzioni del tempo
Le funzioni di s da antitrasformare sono funzioni razionali (rapporto di
polinomi) nella variabile s
F(s) = N(s)
D(s)
28
M. Salerno
Tor Vergata
Laplace
29
Funzioni razionali: notazioni
F(s) = N(s)
D(s)
funzione razionale nella variabile complessa s
m
N(s) = Σ bk
k=0
n
D(s) = Σ ak
k=0
m
sk =
Π (s - zk )
k=1
n
sk =
Π (s - pk )
k=1
p
polinomio
a numeratore di ggrado : gr [N] = m
zk radici di N(s) ; zeri di F(s)
polinomio a denominatore di grado : gr [D] = n
pk radici di D(s) ; poli di F(s)
F(s) funzione razionale reale nella variabile complessa s
F(s) reale per s reale :
coefficienti ak e bk reali
F(s) funzione razionale propria : m = gr [N] < n = gr [D]
F(s) funzione razionale impropria : m = gr [N] > n = gr [D]
s0 polo di F(s) se lim F(s) =
s
s0
∞
poli di F(s)
{∞
pk
radici di D(s)
se gr [N] > gr [D]
M. Salerno
Tor Vergata
Laplace
Caso di funzioni razionali proprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale propria,
con poli pk semplici: radici di D(s) distinte
Sviluppo in frazioni parziali
n
ck
N(s)
F(s) =
=Σ
D(s) k=1 s - pk
ck residuo di F(s) sul polo pk
Calcolo dei residui
n
F(s) =
Σ
k=1
ck
s - pk
30
M. Salerno
Tor Vergata
Laplace
Caso di funzioni razionali proprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale propria,
con poli pk semplici: radici di D(s) distinte
Sviluppo in frazioni parziali
n
ck
N(s)
F(s) =
=Σ
D(s) k=1 s - pk
ck residuo di F(s) sul polo pk
Calcolo dei residui
polo ph
n
n
c
lim (s – ph )F(s) = Σlim kΣ (sc–k ph )(s – ph )
pk s - pk
s ph
s sph- k=1
k=1
30
M. Salerno
Tor Vergata
Laplace
30
Caso di funzioni razionali proprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale propria,
con poli pk semplici: radici di D(s) distinte
Sviluppo in frazioni parziali
n
ck
N(s)
F(s) =
=Σ
D(s) k=1 s - pk
ck residuo di F(s) sul polo pk
Calcolo dei residui
polo ph
nn
n
c
ck
k
lim (s – ph )F(s) = Σlim
lim
(s
–pph )(s – ph ) = ch
Σ
Σ
s
p
s
s ph
s
p
s
p
kh
k
k=1
k=1 h k=1
{ == c0h
per k ≠ h
per k = h
M. Salerno
Tor Vergata
Laplace
Caso di funzioni razionali proprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale propria,
con poli pk semplici: radici di D(s) distinte
Sviluppo in frazioni parziali
n
ck
N(s)
F(s) =
=Σ
D(s) k=1 s - pk
Calcolo dei residui
polo ph
ck residuo di F(s) sul polo pk
ck = lim (s – pk ) F(s)
s pk
nn
n
c
cD(s)
k
k p )(s – p )N (s)
Nota: il termine
(s - (s
pk –) èpun
fattore
del
polinomio
lim
lim
lim
)F(s) = ΣΣs - pΣ (s
–
= ch
h
h
h
s
p
c
=
s
p
s
p
s
p
kh
k
k
k=1
k=1 h k=1
D(s) = (s -hpk ) Dk(s),
Dk(s) s = pk
ove Dk(s) è pari a D(s) privato del fattore (s - pk=) 0
per k ≠ h
= ch per k = h
{
30
M. Salerno
Tor Vergata
Laplace
Caso di funzioni razionali proprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale propria,
con poli pk semplici: radici di D(s) distinte
Sviluppo in frazioni parziali
n
ck
N(s)
F(s) =
=Σ
D(s) k=1 s - pk
ck residuo di F(s) sul polo pk
lim (s(s––ppkk))F(s)
F(s) = N (s)
cckk== lim
Dk(s) s = pk
ss ppkk
polo ph
nn
n
c
cD(s)
k
kp
n )(s – p )N =(s)
Antitrasformazione
Nota: il termine
(s - (s
pk –) èpun
fattore
del
polinomio
lim
lim
lim
)F(s) = Σ
(s
–
ch
Σ
Σ
h
h
h
-1
s
p
s
p
c
=
s
p
s
p
s
p
p
t
-1
at
k h] = Σ
k c e kk u (t)
k=1
k=1
h k=1
[ F(s)
D(s) ==(se -hup-1
Dk(s),f(t) = L
da L [1/(s-a)]
D
k
-1k(s) s = p
k )(t)
k
k=1
e dalla proprietà
linearità
ove Ddi
per k ≠ h
k(s) è pari a D(s) privato del fattore (s - pk=) 0
= ch per k = h
Calcolo dei residui
{
30
M. Salerno
Tor Vergata
Laplace
Caso di funzioni razionali proprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale propria,
con poli multipli: radici di D(s) coincidenti
Sviluppo in frazioni parziali
F(s) = N(s)
D(s)
Lo sviluppo in frazioni parziali nel caso di poli multipli
(noto anche come sviluppo di Hermite) è piuttosto
complesso. Per l’algoritmo si rimanda al libro di testo
Antitrasformata
Si ricorda che:
1
1
-1
---------L [(s-a)n]= (n-1)! tn-1 eat u-1(t)
1 ]= t eat u (t)
L-1[------1
(s-a)2
caso di un polo di ordine n
caso di un polo di ordine 2
31
M. Salerno
Tor Vergata
Laplace
Esempio di antitrasformazione
F(s) =
s+1
s3 + 5s2 + 6s
Fattorizzazione
del denominatore
s3 + 5s2 + 6s =
= s(s2 + 5s + 6) =
s2 + 5s + 6 = 0
s1,2 = ½ (-5 + 52 – 4 . 6 ) = ½ (-5 + 1)
Radici di
32
M. Salerno
Tor Vergata
Laplace
Esempio di antitrasformazione
F(s) =
s+1
s+1
=
s3 + 5s2 + 6s
s (s+2)(s+3)
Fattorizzazione
del denominatore
s3 + 5s2 + 6s =
= s(s2 + 5s + 6) =
= s(s + 2)(s + 3)
s2 + 5s + 6 = 0
s1,2 = ½ (-5 + 52 – 4 . 6 ) = ½ (-5 + 1)
Radici di
32
M. Salerno
Tor Vergata
Laplace
32
Esempio di antitrasformazione
F(s) =
s+1
s+1
=
s3 + 5s2 + 6s
s (s+2)(s+3)
Sviluppo in frazioni parziali
A
B
C
1
= s + s+2 + s+3
s (s+2)(s+3)
3
2
s + 5s + 6s =
s+1
2
= 1/6
A
=
s
F(s)
|
=
= s(s + 5s s=0
+ 6) =
(s+2)(s+3) s=0
= s(s + 2)(s + 3)
B = (s+2) F(s)|s= -2 = s + 1
= 1/2
s= -2
Radici di s2 + 5s + 6 = s(s+3)
0
s1,2= =(s+3)
½ (-5F(s)
+ |s=52-3–=4 .s6+) 1= ½ (-5= +-2/3
1)
C
s(s+2) s= -3
Fattorizzaziones +
F(s)
=
del denominatore
Poli di F(s)
s0 = 0; s1 = -2; s2 = -3
piano s
ω = Im[s]
x x
-3 -2
poli
x
0
σ = Re[s]
M. Salerno
Tor Vergata
Laplace
32
Esempio di antitrasformazione
F(s) =
s+1
s+1
1 + 1 - 2
=
=
6s 2(s+2) 3(s+3)
s3 + 5s2 + 6s
s (s+2)(s+3)
Sviluppo
Antitrasformata
in frazioni parziali
1 1 -2t 2 -3t
f(t)
=
[ 6 +s +2 1e - 3 eA ] uB
Fattorizzazione
C
-1(t)
F(s)
=
=
+
+
del denominatore
s s+2 s+3
s
(s+2)(s+3)
andamento
s3 + 5s2 + 6sf(0=+) = 1/6 + ½ - 2/3 = 0 f(∞ ) = 1/6
s-2(1/2)
+ 1 e –2t + 3(2/3)
2
f(t)
per
e –3t = 0
= 1/6
A
=
s
F(s)
|
=
= s(s + 5s s=0
+ 6)
max=
- e –2t + (s+2)(s+3)
2 e –3t = 0; e t =s=0
2; t = ln 2 = 0.69
= s(s + 2)(sf(t)
+ 3) = f(0.69) = 0.21 > 1/6
max
B = (s+2) F(s)|s= -2 = s + 1
= 1/2
s= -2
Radici di s2f(t)
+ 5s + 6 = s(s+3)
0
1/6
sC1,2= =(s+3)
½ (-5F(s)
+ |s=52-3–=4 .s6+) 1= ½ (-5= +-2/3
1)
0.69
t
s(s+2) s= -3
Poli di F(s)
s0 = 0; s1 = -2; s2 = -3
piano s
ω = Im[s]
x x
-3 -2
poli
x
0
σ = Re[s]
M. Salerno
Tor Vergata
Laplace
Esempio di antitrasformazione
F(s) =
s
s2 + 2s + 5
Fattorizzazione
del denominatore
s2 + 2s + 5 =
s2 + 2s + 5 = 0
s1,2 = -1 + 1 – 5 = -1 + 2j
Radici di
33
M. Salerno
Tor Vergata
Laplace
33
Esempio di antitrasformazione
F(s) =
s
s
=
s2 + 2s + 5
(s+1-2j)(s+1+2j)
Fattorizzazione
del denominatore
s2 + 2s + 5 =
= (s + 1-2j)(s + 1+2j)
2s + 5 = 0
s1,2 = -1 + 1 – 5 = -1 + 2j
Radici di
Poli di F(s)
s1 = -1+2j; s2 = -1-2j
piano s
ω = Im[s]
x
2
-1
s2 +
poli
x
σ = Re[s]
-2
M. Salerno
Tor Vergata
Laplace
33
Esempio di antitrasformazione
F(s) =
s
s
=
s2 + 2s + 5
(s+1-2j)(s+1+2j)
Sviluppo in frazioni parziali
s
Fattorizzazione
F(s) =
(s+1-2j)(s+1+2j)
del denominatore
B
A
= s+1-2j + s+1+2j
s2 + 2s + 5 =
s
A= =(s(s+1-2j)F(s)
|
=
-1+2j
+ 1-2j)(s +s=1+2j)
s+1+2j
-1+2j
= 4j = ½ + ¼ j
s
B
= (s+1+2j)F(s)
5 ==0s+1-2j
Radici
di s2 + 2ss=+-1-2j
|
s1,2= =-1-2j
-1 += ½
1 –- ¼
5 j= -1 + 2j
-4j
s= -1+2j
s= -1-2j
=
Poli di F(s)
s1 = -1+2j; s2 = -1-2j
piano s
ω = Im[s]
x
2
-1
=
poli
x
σ = Re[s]
-2
M. Salerno
Tor Vergata
Laplace
33
Esempio di antitrasformazione
F(s) =
½+¼j ½-¼j
s
s
=
=
+
2
s+1-2j
s+1+2j
s + 2s + 5
(s+1-2j)(s+1+2j)
Sviluppo in frazioni parziali
s
Fattorizzazione
F(s) =
(s+1-2j)(s+1+2j)
del denominatore
B
A
= s+1-2j + s+1+2j
s2 + 2s + 5 =
s
polo
:+-11-2j)(s
+2j ; residuo
A
=
½
+¼j =
A= =(s(s+1-2j)F(s)
|+s=1+2j)
=
-1+2j
s+1+2j s= -1+2j B = A*
polo :-1+2j
-1 - 2j ; residuo B = ½ - ¼ j
= 4j = ½ + ¼ j
}
In generale:
s
ogni funzione5razionale
B
=per
(s+1+2j)F(s)
==0s+1-2jreale (cioè=a
Radici
di s2 + 2ss=+-1-2j
coefficienti reali), a poli complessis=coniugati
-1-2j
-1-2j
s1,2=corrispondono
= -1 += ½
1 –- residui
5 j= -1complessi
+ 2j coniugati
¼
-4j
Poli di F(s)
s1 = -1+2j; s2 = -1-2j
piano s
ω = Im[s]
x
2
-1
|
poli
x
σ = Re[s]
-2
M. Salerno
Tor Vergata
Laplace
33
Esempio di antitrasformazione
F(s) =
½+¼j ½-¼j
s
s
=
=
+
2
s+1-2j
s+1+2j
s + 2s + 5
(s+1-2j)(s+1+2j)
Sviluppo
Antitrasformata
in frazioni parziali
(-1+2j)t + (½ − A
(-1-2j)t ]Bu (t)
s
f(t)
=
[
(½+
¼
j)e
¼
j)e
-1
Fattorizzazione
F(s) =
= s+1-2j + s+1+2j
(s+1-2j)(s+1+2j)
del denominatore
complessi coniugati per ogni t
s2 + 2s + 5 =
s
polo
:+-11-2j)(s
+2j ; residuo
A
=
½
+¼j =
A= =(s(s+1-2j)F(s)
|+s=1+2j)
=
-1+2j
s+1+2j s= -1+2j B = A*
polo :-1+2j
-1 - 2j ; residuo B = ½ - ¼ j
= 4j = ½ + ¼ j
}
In generale:
s
ogni funzione5razionale
B
=per
(s+1+2j)F(s)
==0s+1-2jreale (cioè=a
Radici
di s2 + 2ss=+-1-2j
coefficienti reali), a poli complessis=coniugati
-1-2j
-1-2j
s1,2=corrispondono
= -1 += ½
1 –- residui
5 j= -1complessi
+ 2j coniugati
¼
-4j
Poli di F(s)
s1 = -1+2j; s2 = -1-2j
piano s
ω = Im[s]
x
2
-1
|
poli
x
σ = Re[s]
-2
M. Salerno
Tor Vergata
Laplace
33
Esempio di antitrasformazione
F(s) =
½+¼j ½-¼j
s
s
=
=
+
2
s+1-2j
s+1+2j
s + 2s + 5
(s+1-2j)(s+1+2j)
Sviluppo
Antitrasformata
in frazioni parziali
(-1+2j)t + (½ − A
(-1-2j)t ]Bu (t)
s
f(t)
=
[
(½+
¼
j)e
¼
j)e
-1
Fattorizzazione
F(s) =
= s+1-2j + s+1+2j
(s+1-2j)(s+1+2j)
del denominatore
complessi coniugati per ogni t
s2 + 2s + 5 =
s
polo
:+-11-2j)(s
+2j
;
residuo
A
=
½
+ =¼ j =
A= =(s(s+1-2j)F(s)
|
=
(-1+2j)t
-1+2j
+s=j)e
1+2j)
f(t) = 2 Re[(½+ ¼
] u-1(t)
s+1+2j
s= -1+2j B = A*
polo :-1+2j
-1
2j
;
residuo B = ½ - ¼
j
-t
2jt
=½
+ ¼ ]j u-1(t) =
½ j)e
==e Re
4j [(1+
1+ ½ j =
}
In generale:
0.46 j
-t Re[e j(2t+0.46) ] u (t) =
=
1.12
e
= 1.12
e
ogni funzione5razionale
B
=per
(s+1+2j)F(s)
=0 -1 s reale (cioè=a
=
Radici
di s2 + 2ss=+-1-2j
s+1-2j
-t cos(2t
reali),
a poliu-1complessi
s=coniugati
-1-2j
+
0.46)
(t)
=coefficienti
1.12
e
-1-2j
s1,2=corrispondono
= -1 += ½
1 –- residui
5 j= -1complessi
+ 2j coniugati
¼
-4j
Poli di F(s)
s1 = -1+2j; s2 = -1-2j
piano s
ω = Im[s]
x
2
-1
|
poli
x
σ = Re[s]
-2
M. Salerno
Tor Vergata
Laplace
33
Esempio di antitrasformazione
F(s) =
½+¼j ½-¼j
s
s
=
=
+
2
s+1-2j
s+1+2j
s + 2s + 5
(s+1-2j)(s+1+2j)
Sviluppo
Antitrasformata
in frazioni parziali
-t cos(2t + 0.46)
(-1+2j)t
(-1-2j)t ]Bu (t)
A
f(t)
=
1.12
e
uj)e
s
f(t)
=
[
(½+
¼
j)e
+
(½
−
¼
-1(t)
-1
Fattorizzazione
F(s) =
= s+1-2j + s+1+2j
(s+1-2j)(s+1+2j)
del denominatore
Andamentocomplessi coniugati per ogni t
2
s + 2s + 5f(t)=
s
polo
:+-1
+2j
;
residuo
A
=
½
+¼j =
A= =(s(s+1-2j)F(s)
|
=
1.12
(-1+2j)t
-1+2j
1-2j)(s
+s=j)e
1+2j)
f(t) = 2 Re
[
(½+ ¼
]
u-1(t) =s= -1+2j B = A*
s+1+2j
1- 2j ; residuo B = ½ - ¼ j
polo :-1+2j
-1
=½
+ 2jt
¼ ]j u-1(t) =
½ j)e
==e-t Re
4j [(1+
1+ ½ j =
}
In generale:
0.46
t j
-t Re[e j(2t+0.46) ] u (t) =
=
1.12
e
= 1.12
e
ogni funzione5razionale
B
=per
(s+1+2j)F(s)
=0 -1 s reale (cioè=a
=
Radici
di s2 + 2ss=+-1-2j
s+1-2j
-t cos(2t
reali),
a poliu-1complessi
s=coniugati
-1-2j
+
0.46)
(t)
=coefficienti
1.12
e
-1-2j
-1.12
s1,2=corrispondono
= -1 += ½
1 –- residui
5 j= -1complessi
+ 2j coniugati
¼
-4j
Poli di F(s)
s1 = -1+2j; s2 = -1-2j
piano s
ω = Im[s]
x
2
-1
|
poli
x
σ = Re[s]
-2
M. Salerno
Tor Vergata
Laplace
34
Caso di funzioni razionali improprie
Ipotesi:
F(s) = N(s)
D(s)
funzione razionale reale impropria
gr [N] > gr [D]
Divisione fra polinomi
F(s) = N(s) = Q(s) + R(s)
D(s)
D(s)
gr[Q]
Q(s) = Σ qk sk : polinomio quoziente
k=0
grado : gr [Q] = gr [N] - gr [D]
R(s) : polinomio resto
funzione razionale
propria
Antitrasformazione
da L-1[sk] = uk(t)
e dalla proprietà di linearità
Le funzioni razionali improprie possono
essere antitrasformate solo nell’ambito
della teoria delle distribuzioni
grado : gr [R] < gr [D]
f(t) = L-1 [ F(s) ] =
gr[Q]
L-1 [ k=0
Σ qk sk ] + L-1 [ R(s)
]=
D(s)
gr[Q]
-1
Σ
qk uk(t) + L [ R(s) ]
D(s)
k=0
M. Salerno
Tor Vergata
Laplace
35
Esempio di antitrasformazione
s2 + 3s + 5
F(s) =
s+ 1
Divisione fra polinomi
N(s) = s2 + 3s + 5
D(s) = s + 1
Poli di F(s)
s1 = -1 ; s2 =
s2 + 3s + 5 s + 1
s2 + s
s+ 2
2s + 5
2s + 2
3
∞
M. Salerno
Tor Vergata
Laplace
35
Esempio di antitrasformazione
s2 + 3s + 5
F(s) =
s+ 1
Divisione fra polinomi
s2 + 3s + 5 s + 1
N(s) = s2 + 3s + 5
s2 + s
s+ 2
D(s) = s + 1
2s + 5
2s + 2
Q(s) = s + 2
3
R(s) = 3
3
F(s) = N(s) = Q(s) + R(s) = s + 2 + s + 1
D(s)
D(s)
Poli di F(s)
s1 = -1 ; s2 =
∞
M. Salerno
Tor Vergata
Laplace
35
Esempio di antitrasformazione
s2 + 3s + 5
3
F(s) =
= s+ 2 + s+ 1
s+ 1
Divisione fra polinomi
s2 + 3s + 5 s + 1
N(s) = s2 + 3s + 5
s2 + s
s+ 2
D(s) = s + 1
2s + 5
2s + 2
Q(s) = s + 2
3
R(s) = 3
3
F(s) = N(s) = Q(s) + R(s) = s + 2 + s + 1
D(s)
D(s)
Antitrasformata
f(t) = u1(t) + 2 u0(t) + 3 e-t u-1(t)
Poli di F(s)
s1 = -1 ; s2 =
∞
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
Vu(s) +
+
R
1/sC
L V/s
condizioni iniziali nulle
sL
dominio di s
Analisi nel dominio di s
Poli di Vu(s)
Vu (sC + 1/sL) + (Vu - V/s)/R = 0
Radici di s2 + s/(RC) + 1/(LC) = 0
Vu (sC + 1/sL + 1/R) = V/(sR)
Vu [s2 + s/(RC) + 1/(LC)] = V/(RC)
V
1
Vu = RC
s2 + s/(RC) + 1/(LC)
Discriminante
∆ = 1/(R2 C2 ) – 4 /(LC)
∆>0
poli reali distinti
∆=0
poli reali coincidenti
∆<0
poli complessi coniugati
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
Analisi
V dominio di1s
V = nel
u
RC s2 + s/(RC) + 1/(LC)
Vu (sC + 1/sL) + (Vu - V/s)/R =
3V
1
=
V
=
3V
u
Vu (sC + 1/sL
(s + 1) (s + 2)
s2 + 3+s1/R)
+ 2 = V/(sR)
2reali distinti:
VPoli
u [s + s/(RC) + 1/(LC)] = V/(RC)
-1; -2
V
1
Vu = RC
s2 + s/(RC) + 1/(LC)
Vu(s) +
+
R
1/sC
L V/s
sL
dominio di s
Poli di Vu(s)
Esempio : R= 1/3 ; L = ½ ; C =1
0 Radici di s2 + s/(RC) + 1/(LC) = 0
Discriminante
∆ = 1/(R2 C2 ) – 4 /(LC)
∆>0
poli reali distinti
∆=0
poli reali coincidenti
∆<0
poli complessi coniugati
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
+
L V/s
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
Esempio : R= 1/3 ; L = ½ ; C =1
u
RC s2 + s/(RC) + 1/(LC)
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s2 + s/(RC) + 1/(LC) = 0
B
3V
3V
A
3V
1
=
=
+
=
V
=
3V
Vuu (sC + 1/sL
s+
1 s+2
(s + 1) (s + 2) s + 1 s + 2Discriminante
s2 + 3+s1/R)
+ 2 = V/(sR)
2
2
∆ = 1/(R C ) – 4 /(LC)
2
reali distinti:
VPoli
u [s + s/(RC) + 1/(LC)] = V/(RC)
3V
A
=
= 3Vpoli reali distinti
-1; -2
s + 2 ∆s =>-10
V
1
poli reali coincidenti
Vu = RC
3V ∆ = 0
2
B=
= - 3V
s + s/(RC) + 1/(LC)
s + 1 ∆s =<-20
poli complessi coniugati
Analisi
V dominio di1s
V = nel
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
+
L V/s
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
Esempio : R= 1/3 ; L = ½ ; C =1
u
RC s2 + s/(RC) + 1/(LC)
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s2 + s/(RC) + 1/(LC) = 0
B
3V
3V
A
3V
1
=
=
+
=
V
=
3V
Vuu (sC + 1/sL
s+
1 s+2
(s + 1) (s + 2) s + 1 s + 2Discriminante
s2 + 3+s1/R)
+ 2 = V/(sR)
2
2
∆ = 1/(R C ) – 4 /(LC)
2
reali distinti:
VPoli
u [s + s/(RC) + 1/(LC)] = V/(RC) v (t) 3V
A =u
= 3Vpoli reali distinti
-1; -2
s + 2 ∆s =>-10
V
1
poli reali coincidenti
V
=
3V ∆ = 0
vuu(t) = RC
3V (es-t2–+e-2ts/(RC)
) u-1(t) + 1/(LC)
B=
= - 3V
s + 1 ∆s =<-20
poli complessit coniugati
Analisi
V dominio di1s
V = nel
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
+
L V/s
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
1/4 ; L = ½
1/4; ;CC=1
=1
Esempio : R= 1/3
u
RC s2 + s/(RC) + 1/(LC)
2
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s + s/(RC) + 1/(LC) = 0
B
3V
3V
A
3V
1
=
=
+
=
V
=
3V
11/R)
41)V(s + 2) s + 1 s + 2Discriminante
u (sC + 1/sL
VuV
+
=
V/(sR)
s+
1 s+2
=
(s
+
s2 +
3
s
+
2
u=4V
2
2
2
2
s +4s+4
(s + 2)
∆ = 1/(R C ) – 4 /(LC)
2
Poli
reali
distinti:
+ s/(RC)
+ 1/(LC)] = V/(RC)
VPolo
u [s reale
doppio:
v=u(t) 3V ∆ > 0 = 3V
A
poli reali distinti
-1;-2-2
s + 2 s = -1
V
1
poli reali coincidenti
V
=
3V ∆ = 0
vuu(t) = RC
3V (es-t2–+e-2ts/(RC)
) u-1(t) + 1/(LC)
B=
= - 3V
s + 1 ∆s =<-20
poli complessit coniugati
Analisi
V dominio di1s
V = nel
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
+
L V/s
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
1/4 ; L = ½
1/4; ;CC=1
=1
Esempio : R= 1/3
u
RC s2 + s/(RC) + 1/(LC)
2
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s + s/(RC) + 1/(LC) = 0
B
3V
3V
A
3V
1
=
=
+
=
V
=
3V
11/R)
41)V(s + 2) s + 1 s + 2Discriminante
u (sC + 1/sL
VuV
+
=
V/(sR)
s+
1 s+2
=
(s
+
s2 +
3
s
+
2
u=4V
2
2
2
2
s +4s+4
(s + 2)
∆ = 1/(R C ) – 4 /(LC)
2
Poli
reali
distinti:
+ s/(RC)
+ 1/(LC)] = V/(RC)
VPolo
u [s reale
doppio:
v=u(t) 3V ∆ > 0 = 3V
A
poli reali distinti
-1;-2-2
s + 2 s = -1
V
1
poli reali coincidenti
V
=
3V ∆ = 0
3V
4 V(e
t s-te2-2t
–+eu-2t
(t)
)
u
(t)
vuu(t) = RC
B=
= - 3V
-1
-1
s/(RC)
+ 1/(LC)
s + 1 ∆s =<-20
poli complessit coniugati
Analisi
V dominio di1s
V = nel
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
+
L V/s
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
1/4 ; L = ½
1/2
1/4; ;CC=1
1/2
=1
Esempio : R= 1/3
u
RC s2 + s/(RC) + 1/(LC)
2
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s + s/(RC) + 1/(LC) = 0
B
3V
3V
A
1
2V
3V
=
=
+
=
V
=
2V
3V
11/R)
41)
V(s(s+ +2)1+j)s + 1 s + 2Discriminante
u (sC + s
VuuV
1/sL
+
=
V/(sR)
s+
1 s+2
2
s
+
2
=
(s
+
1-j)
s22 ++
3
s
+
2
u=4V
2
2
2
2
s +4s+4
(s + 2)
∆ = 1/(R C ) – 4 /(LC)
2
complessi
reali
distinti:
+ s/(RC)
+coniugati:
1/(LC)] = V/(RC)
VPoli
u [s reale
Polo
doppio:
v=u(t) 3V ∆ > 0 = 3V
A
poli reali distinti
-1;-1+j
s + 2 s = -1
-2-2 ; -1-j
V
1
poli reali coincidenti
V
=
3V ∆ = 0
3V
4 V(e
t s-te2-2t
–+eu-2t
(t)
)
u
(t)
vuu(t) = RC
B=
= - 3V
-1
-1
s/(RC)
+ 1/(LC)
s + 1 ∆s =<-20
poli complessit coniugati
Analisi
V dominio di1s
V = nel
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
condizioni iniziali nulle
+
L V/s
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
1/4 ; L = ½
1/2
1/4; ;CC=1
1/2
=1
Esempio : R= 1/3
u
RC s2 + s/(RC) + 1/(LC)
2
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s + s/(RC) + 1/(LC) = 0
A A B
1
2V
A*3V - 3V
3V
=
=
+
=
V
=
2V
=
+
3V
Discriminante
11/R)
41)
V(s(s+ +2)1+j)s + 1s + 1-j
u (sC + s
VuuV
1/sL
+
=
V/(sR)
s
+
2
+
1 s+2
s +2 s1+j
2
s
+
2
=
(s
+
1-j)
s22 ++
3
s
+
2
u=4V
2
2
2
s +4s+4
(s + 2)
∆ = 1/(R C ) – 4 /(LC)
2
complessi
reali
distinti:
+ s/(RC)
+coniugati:
1/(LC)] = V/(RC)
VPoli
u [s reale
Polo
doppio:
3V
v=u(t)2V
A
A = s + 2 ∆ > 0 ==3V
-jpoli
V reali distinti
-1;-1+j
-2-2 ; -1-j
s
=
-1
s + 1+j s = -1+j
V
1
poli reali coincidenti
3V ∆ = 0
3V
4 V(e
t s-te2-2t
–+eu-2t
(t)
)
u
(t)
vVuu(t)== RC
B=
= - 3V
-1
-1
s/(RC)
+ 1/(LC)
s + 1 ∆s =<-20
poli complessit coniugati
Analisi
V dominio di1s
V = nel
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
+
L V/s
condizioni iniziali nulle
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
1/4 ; L = ½
1/2
1/4; ;CC=1
1/2
=1
Esempio : R= 1/3
u
RC s2 + s/(RC) + 1/(LC)
2
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s + s/(RC) + 1/(LC) = 0
jV3V
3V
A -jV
1
2V
3V
A B ++ = A*
=
=
+
V
=
2V
=
=
3V
Discriminante
11/R)
41)
V(s(s+ +2)1+j)s + 1ss ++ 1-j
u (sC + s
VuuV
1/sL
+
=
V/(sR)
s
+
2
+
1 s+2
1-j
1+j
ss +2+s1+j
2
s
+
2
=
(s
+
1-j)
s22 ++
3
s
+
2
u=4V
2
2
2
s +4s+4
(s + 2)
∆ = 1/(R C ) – 4 /(LC)
2
complessi
reali
distinti:
+ s/(RC)
+coniugati:
1/(LC)] = V/(RC)
VPoli
u [s reale
Polo
doppio:
3V
v=u(t)2V
A
A = s + 2 ∆ > 0 ==3V
-jpoli
V reali distinti
-1;-1+j
-2-2 ; -1-j
s
=
-1
s + 1+j s = -1+j
V
1
∆ [-j
= 0e j t ] u
poli(t)reali
coincidenti
(-1+j) t ] u (t) = 2 Ve
- t Re
===RC
3V
vuuu(t)
(t)
V-2t
e
=
2-2t
3V
42VRe
(e
t s-te[-j
–+eu
(t)
)
u
(t)
vV
-1
B=
= - 3V
-1
-1
s/(RC)
+ -11/(LC)
s
+
1
s = -20 - t poli complessit coniugati
= 2 Ve- t Re [-j (cos t +j sin t) ] u (t) =∆2<Ve
sin t u (t)
Analisi
V dominio di1s
V = nel
-1
-1
M. Salerno
Tor Vergata
Laplace
36
Esempio: circuito RLC
+
V u-1(t)
dominio di t
vu(t) +
R
C
+
L V/s
condizioni iniziali nulle
Vu(s) +
R
1/sC
sL
dominio di s
Poli di Vu(s)
1/4 ; L = ½
1/2
1/4; ;CC=1
1/2
=1
Esempio : R= 1/3
u
RC s2 + s/(RC) + 1/(LC)
2
Vu (sC + 1/sL) + (Vu - V/s)/R = 0 Radici di s + s/(RC) + 1/(LC) = 0
jV3V
3V
A -jV
1
2V
3V
A B ++ = A*
=
=
+
V
=
2V
=
=
3V
Discriminante
11/R)
41)
V(s(s+ +2)1+j)s + 1ss ++ 1-j
u (sC + s
VuuV
1/sL
+
=
V/(sR)
s
+
2
+
1 s+2
1-j
1+j
ss +2+s1+j
2
s
+
2
=
(s
+
1-j)
s22 ++
3
s
+
2
u=4V
2
2
2
s +4s+4
(s + 2)
∆ = 1/(R C ) – 4 /(LC)
2
complessi
reali
distinti:
+ s/(RC)
+coniugati:
1/(LC)] = V/(RC)vu(t) 3V
VPoli
u [s reale
Polo
doppio:
∆ > 0 ==3V
AA
= v=u(t)s2V
-jpoli
V reali distinti
-1;-1+j
-2
;
-1-j
+
2
-2
s
=
-1
s + 1+j s = -1+j
V
1
∆ [-j
= 0e j t ] u
poli(t)reali
coincidenti
t-2t
(-1+j)
t ] u (t) = 2 Ve
- t Re
===RC
-2tte(t)
3V
vuuu(t)
(t)
Re
V
u
(t)
=
2–sin
t
3V
42VVe
(e
t s--te[-j
e
u
)
u
(t)
vV
-1
-1
B=
= - 3V
-1
+ -1s/(RC)
+ -11/(LC)
s + 1 ∆s =<-20 - t poli complessit coniugati
t
= 2 Ve Re [-j (cos t +j sin t) ] u (t) = 2 Ve sin t u (t)
Analisi
V dominio di1s
V = nel
-1
-1
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
Vu(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
t=0
Vu(s) [s(C+C1)+G +G1] = (sC1+G1 ) V/s
C
C
sC1 1 sC
G
R
sC1+G1
Vu(s) = V
s s(C+C )+G +G
1
dominio di st
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
1
Poli : s0 = 0 ; s1 = -(G+G1 ) / (C+C1 )
Sviluppo in frazioni parziali
Vu(s) =
A=
sC1+G1
B
V
= A
+
C+C1 s [s+(G +G1 ) / (C+C1 )] s s+(G +G1 ) / (C+C1 )
sC1+G1
G1
V
=V
C+C1 s+(G +G1 ) / (C+C1 ) s = 0 G +G1
C1
G1
G+G1
V sC1+G1
V
=
V
=
C
+G
B=
G+G1
1
1
s
s=C+C1
G+G
C+C
C+C1 G+G1
1
1
C+C
1
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
Vu(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
t=0
Vu(s) [s(C+C1)+G +G1] = (sC1+G1 ) V/s
C
C
sC1 1 sC
G
R
sC1+G1
Vu(s) = V
s s(C+C )+G +G
1
dominio di st
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
1
Poli : s0 = 0 ; s1 = -(G+G1 ) / (C+C1 )
Antitrasformata
Sviluppo
in frazioni parziali
C1
G1
G1
B
A
V (s) = V+
sC +G1
con AA = V
Be B = V
=
+
)
G
+G
Vuu(s) = s s+(G +G1 )1 / (C+C
G+G1
C+C
1
1
1
s
s+(G
+G
C+C1 s [s+(G +G1 ) / (C+C
)]
)
/
(C+C
)
1
1
1
C1
G1
-t (G +G1 ) / (C+C1 )
G
vu(t) = V V 1 + sC1+G
e
u-1(t)
G1
1
G +G1
C+C1 G+G1 = V
A=
C+C1 s+(G
G +G1
+G1 ) / (C+C
1) s=0
C
C1
G1
vu(0+) = VV 1 sC +G
partizione capacitiva V se G+G
C
G11C
G1 C1 = G
1
1
1 =
C+C
1
=
V
=
C
+G
B=
G+G1
C+C1 G+G
1
11
s
s
=
C+CG
G+G
C+C
C+C1 G+G1
1
1
1
1
vu(∞) = V
partizioneC+C
resistiva
1
partitore compensato
R1 C1 = R C
G +G1
{
}
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
Vu(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
t=0
Vu(s) [s(C+C1)+G +G1] = (sC1+G1 ) V/s
C
C
sC1 1 sC
G
R
sC1+G1
Vu(s) = V
s s(C+C )+G +G
1
dominio di st
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
{
1
Poli : s0 = 0 ; s1 = -(G+G1 ) / (C+C1 )
}
Andamento
Sviluppo
Antitrasformata
in frazioni parziali
C1
G1
-t (G +G1 ) / (C+C1 )
G1
C1
v
(t)
=
V
+
e
uG-11(t)
G
B
u
A
1
V (s) = V+
sC +G1G +G1 conC+C
e B=V
AA+1= VG+G
1 B
=
)
G
+G
Vuu(s) = s s+(G +G1 )1 / (C+C
G+G1
C+C
1
1
1
s
s+(G
+G
C+C1 s [s+(G +G1 ) / (C+C
)]
)
/
(C+C
)
1
1
1
v
(t)
C
u
1
vu(0+) = VG1
C1
G1
-t (G +G1 ) / (C+C1 )
vu(t) = V V C+C1+ sC1+G
e
u-1(t)
G1
1
G +G1
C+C1 G+G1 = V
A = capacitiva
partizione
)
C+C1 s+(G
/ (C+C
G +G1
+G1v)u(∞
1) s=0
C
C1
G1
vu(0+) = VV 1GsC
partizione
capacitiva
se
+G
C
G11C
G+G
G1 C1 = G
V
1 =
vuB(∞=) = VC+C11 1 1
=
V
=
C
+G
G+G1
C+C1 G+G
1
11
+G
s
s
=
C+CG
G+G
C+C
C+C1 G+G1t
1
1
1
1
1
vupartizione
(∞) = V resistiva partizioneC+C
resistiva
1
+
)1 = R C
vu(0 ) > vR
partitore compensato
G +G1
u(∞
1C
{
}
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
Vu(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
t=0
Vu(s) [s(C+C1)+G +G1] = (sC1+G1 ) V/s
C
C
sC1 1 sC
G
R
sC1+G1
Vu(s) = V
s s(C+C )+G +G
1
dominio di st
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
{
1
Poli : s0 = 0 ; s1 = -(G+G1 ) / (C+C1 )
}
Andamento
Sviluppo
Antitrasformata
in frazioni parziali
C1
G1
-t (G +G1 ) / (C+C1 )
G1
C1
v
(t)
=
V
+
e
uG-11(t)
G
B
u
A
1
V (s) = V+
sC +G1G +G1 conC+C
e B=V
AA+1= VG+G
1 B
=
)
G
+G
Vuu(s) = s s+(G +G1 )1 / (C+C
G+G1
C+C
1
1
1
s
s+(G
+G
C+C1 s [s+(G +G1 ) / (C+C
)]
)
/
(C+C
)
1
1
1
v
(t)
C
u
1
vu(0+) = VG1
C1
G1
-t (G +G1 ) / (C+C1 )
vu(t) = V V C+C1+ sC1+G
e
u-1(t)
G1
1
G +G1
C+C1 G+G1 = V
A = capacitiva
partizione
)
C+C1 s+(G
/ (C+C
G +G1
+G1v)u(∞
1) s=0
C
C1
G1
vu(0+) = VV 1GsC
partizione
capacitiva
se
+G
C
G11C
G+G
G1 C1 = G
V
1 =
vuB(∞=) = VC+C11 1 1
=
V
=
C
+G
G+G1
C+C1 G+G
1
11
+G
s
s
=
C+CG
G+G
C+C
C+C1 G+G1t
1
1
1
1
1
vupartizione
(∞) = V resistiva partizioneC+C
resistiva
1
+
)1 = R C
partitore compensato
vu(0 ) <
> vR
G +G1
u(∞
1C
{
}
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
Vu(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
t=0
Vu(s) [s(C+C1)+G +G1] = (sC1+G1 ) V/s
C
C
sC1 1 sC
G
R
sC1+G1
Vu(s) = V
s s(C+C )+G +G
1
dominio di st
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
{
1
Poli : s0 = 0 ; s1 = -(G+G1 ) / (C+C1 )
}
Andamento
Sviluppo
Antitrasformata
in frazioni parziali
C1
G1
-t (G +G1 ) / (C+C1 )
G1
C1
v
(t)
=
V
+
e
uG-11(t)
G
B
u
A
1
V (s) = V+
sC +G1G +G1 conC+C
e B=V
AA+1= VG+G
1 B
=
)
G
+G
Vuu(s) = s s+(G +G1 )1 / (C+C
G+G1
C+C
1
1
1
s
s+(G
+G
C+C1 s [s+(G +G1 ) / (C+C
)]
)
/
(C+C
)
1
1
1
v
(t)
C
u
1
vu(0+) = VG1
C1
G1
-t (G +G1 ) / (C+C1 )
vu(t) = V V C+C1+ sC1+G
e
u-1(t)
G1
1
G +G1
C+C1 G+G1 = V
A = capacitiva
partizione
)
C+C1 s+(G
/ (C+C
G +G1
+G1v)u(∞
1) s=0
C
C1
G1
vu(0+) = VV 1GsC
partizione
capacitiva
se
+G
C
G11C
G+G
G1 C1 = G
V
1 =
vuB(∞=) = VC+C11 1 1
=
V
=
C
+G
G+G1
C+C1 G+G
1
11
+G
s
s
=
C+CG
G+G
C+C
C+C1 G+G1t
1
1
1
1
1
vupartizione
(∞) = V resistiva partizioneC+C
resistiva
1
+
)1 = R C
partitore compensato
vu(0 ) =
> vR
<
partitore compensato
G +G1
u(∞
1C
{
}
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
VApplicazioni:
u(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
i due resistori e il condensatore C,
VAssegnati
u(s) [s(C+C1)+G +G1] = (sC1+G1 ) V/s
t=0
C
C
sC1 1 sC
dominio di st
G
R
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
{
parassita, la tensione vu(t) è distorta rispetto
alla tensione del
(partitore
non
sC1+G
V generatore
1
V
(s)
=
u
compensato).
s s(C+C )+G +G
Ponendo C1 , tale che R1 C1 1 = R C , si1 ottiene
vu(t)
priva
Poli
: s0di= distorsioni
0 ; s1 = -(G+G1 ) / (C+C1 )
}
Andamento
Sviluppo
Antitrasformata
in frazioni parziali
C1
G1
-t (G +G1 ) / (C+C1 )
G1
C1
v
(t)
=
V
+
e
uG-11(t)
G
B
u
A
1
V (s) = V+
sC +G1G +G1 conC+C
e B=V
AA+1= VG+G
1 B
=
)
G
+G
Vuu(s) = s s+(G +G1 )1 / (C+C
G+G1
C+C
1
1
1
s
s+(G
+G
C+C1 s [s+(G +G1 ) / (C+C
)]
)
/
(C+C
)
1
1
1
v
(t)
C
u
1
vu(0+) = VG1
C1
G1
-t (G +G1 ) / (C+C1 )
vu(t) = V V C+C1+ sC1+G
e
u-1(t)
G1
1
G +G1
C+C1 G+G1 = V
A = capacitiva
partizione
)
C+C1 s+(G
/ (C+C
G +G1
+G1v)u(∞
1) s=0
C
C1
G1
vu(0+) = VV 1GsC
partizione
capacitiva
se
+G
C
G11C
G+G
G1 C1 = G
V
1 =
vuB(∞=) = VC+C11 1 1
=
V
=
C
+G
G+G1
C+C1 G+G
1
11
+G
s
s
=
C+CG
G+G
C+C
C+C1 G+G1t
1
1
1
1
1
vupartizione
(∞) = V resistiva partizioneC+C
resistiva
1
+
)1 = R C
partitore compensato
vu(0 ) =
> vR
<
partitore compensato
G +G1
u(∞
1C
{
}
M. Salerno
Tor Vergata
Laplace
Esempio: partitore
G
R1
V
Vs
37
+
Vu(s)
VApplicazioni:
u(s)(sC+G) + [Vu(s) – V/s](sC1+G1) = 0
Assegnati
i due)+G
resistori
il=condensatore
C,
due condensatori,
possono
VDati
+G1ie]resistori
(sC1+G
u(s) i[s(C+C
1
1 ) V/s
t=0
C
C
sC1 1 sC
dominio di st
G
R
ammettenze
condizioni
iniziali nulle
conduttanze Gi = 1/Ri
{
parassita, la tensione
vu(t)diè dispersione
distorta rispetto
rappresentare
le correnti
fra le
alla tensione
del
(partitore
non
sC1+G
V generatore
armature.
Appena
applicata
la1tensione
di
V
(s)
=
u
compensato).
s partizione
alimentazione,
la
dipende
+G1dai
s(C+C1 )+G
Ponendo C1 , tale
che
R1 C1 = R C dipende
, si ottiene
condensatori.
Dopo
il transitorio,
vu(t)
priva
di= distorsioni
Poli
: s0resistori
0 ; s1di= dispersione.
-(G+G1 ) / (C+C1 )
invece
dai
}
Andamento
Sviluppo
Antitrasformata
in frazioni parziali
C1
G1
-t (G +G1 ) / (C+C1 )
G1
C1
v
(t)
=
V
+
e
uG-11(t)
G
B
u
A
1
V (s) = V+
sC +G1G +G1 conC+C
e B=V
AA+1= VG+G
1 B
=
)
G
+G
Vuu(s) = s s+(G +G1 )1 / (C+C
G+G1
C+C
1
1
1
s
s+(G
+G
C+C1 s [s+(G +G1 ) / (C+C
)]
)
/
(C+C
)
1
1
1
v
(t)
C
u
1
vu(0+) = VG1
C1
G1
-t (G +G1 ) / (C+C1 )
vu(t) = V V C+C1+ sC1+G
e
u-1(t)
G1
1
G +G1
C+C1 G+G1 = V
A = capacitiva
partizione
)
C+C1 s+(G
/ (C+C
G +G1
+G1v)u(∞
1) s=0
C
C1
G1
vu(0+) = VV 1GsC
partizione
capacitiva
se
+G
C
G11C
G+G
G1 C1 = G
V
1 =
vuB(∞=) = VC+C11 1 1
=
V
=
C
+G
G+G1
C+C1 G+G
1
11
+G
s
s
=
C+CG
G+G
C+C
C+C1 G+G1t
1
1
1
1
1
vupartizione
(∞) = V resistiva partizioneC+C
resistiva
1
+
)1 = R C
partitore compensato
vu(0 ) =
> vR
<
partitore compensato
G +G1
u(∞
1C
{
}
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Generatori indipendenti
(di tensione e di corrente)
Condizioni iniziali
(su induttori e condensatori)
Dominio di Laplace
Generatori indipendenti
(di tensione e di corrente)
e(t) = L -1[ E(s) ]
Funzione di eccitazione (tensione o corrente)
In un circuito deve essere
presente almeno una funzione
di eccitazione diversa da zero
Un circuito privo di generatori
indipendenti e con condizioni
iniziali tutte nulle rimane a riposo
I generatori controllati non danno luogo a funzioni di eccitazione
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Generatori indipendenti
(di tensione e di corrente)
Condizioni iniziali
(su induttori e condensatori)
Dominio di Laplace
Generatori indipendenti
(di tensione e di corrente)
e(t) = L -1[ E(s) ]
Funzione di eccitazione (tensione o corrente)
In un circuito deve essere
Un circuito privo di generatori
1
[ U(s) ]e con condizioni
u(t)
=L indipendenti
presente almeno una
funzione
di eccitazione diversa da zero iniziali tutte nulle rimane a riposo
Risposta (tensione o corrente)
I generatori controllati non danno luogo a funzioni di eccitazione
qualunque grandezza elettrica d’interesse del circuito
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Generatori indipendenti
circuito
e(t)
u(t)
(di tensione
e di corrente)
nel dominio
Condizioni
del tempoiniziali
Dominio di Laplace
circuito
E(s)
U(s)
Generatori
indipendenti
nel dominio
(di tensione
e di corrente)
di Laplace
(su induttori e condensatori)
L -1[ E(s)
] = L -1[ E(s)
E(s)] F(s) = U(s)
e(t)
Funzione
eccitazione
(tensione
o corrente)
u(t) = L -1di
[ U(s)
]
F(s) funzione
di rete
In unche
circuito
essere eccitazione
Un circuito
privo di generatori
1
Si suppone
E(s) deve
sia l’unica
presente
[ eccitazione
U(s) ]e con
u(t)
=L indipendenti
presente dal
almeno
una
funzione
condizioni
F(s) dipende
circuito
e dalla coppia
/ risposta
di eccitazione diversa da zero iniziali tutte nulle rimane a riposo
Risposta
(tensione
E(s) e U(s) sono
trasformate
di Laplace di o
e(t)corrente)
e u(t), rispettivamente
e(t) =
I generatori controllati non danno luogo a funzioni di eccitazione
F(s)qualunque
non è una trasformata
di elettrica
Laplace d’interesse del circuito
grandezza
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Dominio di Laplace
Generatori indipendenti
circuito
e(t)
u(t)
(di tensione
e di corrente)
nel dominio
Condizioni
del tempoiniziali
V
circuito
V
(s)
E(s)
U(s)
u(s)
eGeneratori
indipendenti
U(s)
VE(s)
=V
nelF(s)
dominio
e(s)
u(s)
(di tensione
e di corrente)
di Laplace
(su induttori e condensatori)
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s)
e(t) =
Ve(s)F(s)
= V-1udi
Funzione
eccitazione
(tensione
o corrente)
u(t) = L
[(s)U(s)
]
F(s) funzione
di rete
]
F(s) funzione di rete
funzione di trasferimento
inIn
tensione
unche
circuito
essere eccitazione
Un circuito
privo di generatori
Si suppone
E(s) deve
sia l’unica
presente
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s) dipende
circuito
e dalla coppia
eccitazione
/ risposta
di eccitazione diversa da zero iniziali tutte nulle rimane a riposo
1
u(t) =L [ U(s) ]
Risposta
(tensione
E(s) e U(s) sono
trasformate
di Laplace di o
e(t)corrente)
e u(t), rispettivamente
I generatori controllati non danno luogo a funzioni di eccitazione
F(s)qualunque
non è una trasformata
di elettrica
Laplace d’interesse del circuito
grandezza
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Dominio di Laplace
Generatori indipendenti
circuito
e(t)
u(t)
(di tensione
e di corrente)
nel dominio
Condizioni
del tempoiniziali
V
IU(s)
(s)
circuito
V
IE(s)
(s)
uu(s)
eGeneratori
e(s)
indipendenti
VIE(s)
=V
IU(s)
(s)
nelF(s)
dominio
e(s)
uu(s)
(di tensione
e di corrente)
di Laplace
(su induttori e condensatori)
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s)
e(t) =
Ve(s)F(s)
= V-1udi
Funzione
eccitazione
(tensione
o corrente)
u(t) = L
[(s)U(s)
]
F(s) funzione
di rete
]
F(s) funzione di rete
funzione di trasferimento
inIn
tensione
unche
circuito
essere eccitazione
Un circuito
privo di generatori
Si suppone
E(s) deve
sia l’unica
presente
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s) dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
(s)F(s)
=
I
(s)
di eccitazione diversa da ezero inizialiututte nulle rimane a riposo
E(s) e U(s) sono trasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
I generatori controllati non in
danno
luogo a funzioni di eccitazione
corrente
F(s)qualunque
non è una trasformata
di elettrica
Laplace
grandezza
d’interesse del circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Dominio di Laplace
Generatori indipendenti
circuito
e(t)
u(t)
(di tensione
e di corrente)
nel dominio
Condizioni
del tempoiniziali
V
IU(s)
(s)
circuito
V
IE(s)
uu(s)
eGeneratori
e(s)
e(s)
indipendenti
VV
IE(s)
(s)F(s)
Y(s)
== V
IU(s)
Iuu(s)
(s)
nel
dominio
ee(s)
(di tensione
e di corrente)
di Laplace
(su induttori e condensatori)
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s)
e(t) =
Ve(s)F(s)
= V-1udi
Iu(s) funzione
Funzione
eccitazione
o corrente)
u(t) = L
[(s)U(s)
] Ve(s)Y(s) =(tensione
F(s)
di rete
]
F(s) funzione di rete
funzione di trasferimento
ammettenza di
inIn
tensione
unche
circuito
esseretrasferimento
Un circuito
privo di generatori
Si suppone
E(s) deve
sia l’unica
eccitazione
presente
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s) dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
(s)F(s)
=
I
(s)
di eccitazione diversa da ezero inizialiututte nulle rimane a riposo
E(s) e U(s) sono trasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
I generatori controllati non in
danno
luogo a funzioni di eccitazione
corrente
F(s)qualunque
non è una trasformata
di elettrica
Laplace
grandezza
d’interesse del circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Dominio di Laplace
Generatori indipendenti
circuito
e(t)
u(t)
(di tensione
e di corrente)
nel dominio
Condizioni
del tempoiniziali
V
IU(s)
(s)
circuito
IE(s)
V
uu(s)
eGeneratori
e(s)
e(s)
indipendenti
VIV
IE(s)
(s)Z(s)
F(s)
Y(s)
===VV
IU(s)
Iuu(s)
(s)
nel
dominio
ee(s)
e(s)
(di tensione
e di corrente)
di Laplace
(su induttori e condensatori)
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s)
e(t) =
Ve(s)F(s)
= V-1udi
Iu(s) funzione
Funzione
eccitazione
o corrente)
u(t) = L
[(s)U(s)
] Ve(s)Y(s) =(tensione
F(s)
di rete
]
F(s) funzione di rete
funzione di trasferimento
ammettenza di
inIn
tensione
unche
circuito
esseretrasferimento
Un circuito
privo di generatori
Si suppone
E(s) deve
sia l’unica
eccitazione
presente
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s)
dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
Ie(s)Z(s)
=
V
(s)
(s)F(s)
=
I
(s)
u diversa da ezero
di eccitazione
inizialiututte nulle rimane a riposo
E(s) eimpedenza
U(s) sonoditrasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
I generatori controllati non in
danno
luogo a funzioni di eccitazione
trasferimento
corrente
F(s)qualunque
non è una trasformata
di elettrica
Laplace
grandezza
d’interesse del circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Dominio del tempo
Dominio di Laplace
Generatori indipendenti
circuito
e(t)
u(t)
(di tensione
e di corrente)
nel dominio
Condizioni
del tempoiniziali
V
IU(s)
(s)
circuito
IE(s)
V
uu(s)
eGeneratori
e(s)
e(s)
indipendenti
VIV
IE(s)
(s)Z(s)
F(s)
Y(s)
===VV
IU(s)
Iuu(s)
(s)
nel
dominio
ee(s)
e(s)
(di tensione
e di corrente)
di Laplace
(su induttori e condensatori)
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s) Se la tensione e la
e(t) =
Ve(s)F(s)
= V-1udi
Iu(s) funzione
Funzione
eccitazione
o corrente)
u(t) = L
[(s)U(s)
] Ve(s)Y(s) =(tensione
F(s)
di rete
]
F(s) funzione
di rete
corrente si riferiscono
funzione di trasferimento
ammettenza di
alla stessa coppia di
ingresso
inIn
tensione
trasferimento
un
circuito
deve
essere
Un
circuito
privo
di generatori
Si suppone che E(s) sia l’unica eccitazione presente
morsetti, le impedenze
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s)
dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
Ie(s)Z(s)
=
V
(s)
(s)F(s)
=
I
(s)
e
le ammettenze
u diversa da ezero
di eccitazione
inizialiututte nulle rimane
a riposo
E(s) eimpedenza
U(s) sonoditrasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
sono dette
Iingresso
generatori controllati non in
danno
luogo a funzioni di eccitazione
trasferimento
corrente
ingresso
F(s)qualunque
non
è una trasformata
di elettrica
Laplace
grandezza
d’interesse deldi circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Esempio
Dominio del tempo
sL Ie di
= VLaplace
u
Dominio
Generatori indipendenti
+
R
R
circuito
e(t)
u(t)
(di tensione e di corrente)
Vu
Ie
nel dominio
sL
Condizioni
del tempoiniziali
(su induttori e condensatori)
sL
impedenza di trasferimento
V
IU(s)
(s)
circuito
IE(s)
V
uu(s)
eGeneratori
e(s)
e(s)
indipendenti
VIV
IE(s)
(s)Z(s)
F(s)
Y(s)
===VV
IU(s)
Iuu(s)
(s)
nel
dominio
ee(s)
e(s)
(di tensione
e di corrente)
di Laplace
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s) Se la tensione e la
e(t) =
Ve(s)F(s)
= V-1udi
Iu(s) funzione
Funzione
eccitazione
o corrente)
u(t) = L
[(s)U(s)
] Ve(s)Y(s) =(tensione
F(s)
di rete
]
F(s) funzione
di rete
corrente si riferiscono
funzione di trasferimento
ammettenza di
alla stessa coppia di
ingresso
inIn
tensione
trasferimento
un
circuito
deve
essere
Un
circuito
privo
di generatori
Si suppone che E(s) sia l’unica eccitazione presente
morsetti, le impedenze
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s)
dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
Ie(s)Z(s)
=
V
(s)
(s)F(s)
=
I
(s)
e
le ammettenze
u diversa da ezero
di eccitazione
inizialiututte nulle rimane
a riposo
E(s) eimpedenza
U(s) sonoditrasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
sono dette
Iingresso
generatori controllati non in
danno
luogo a funzioni di eccitazione
trasferimento
corrente
ingresso
F(s)qualunque
non
è una trasformata
di elettrica
Laplace
grandezza
d’interesse deldi circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Esempio
Dominio del tempo
Vu +
Generatori indipendenti
+
R
R
circuito
e(t)
u(t)
(di tensione e di corrente)
Vu
Ie
nel dominio
sL
Condizioni
del tempoiniziali
(su induttori e condensatori)
sL Ie di
= VLaplace
u
Dominio
sL
impedenza di trasferimento
(R+sL) Ie = Vu
V
IU(s)
(s)
circuito
IE(s)
V
(s)
(s)
uu(s)
di
ingresso
eGeneratori
eeR+sL impedenza
indipendenti
VIV
IE(s)
(s)Z(s)
F(s)
Y(s)
===VV
IU(s)
Iuu(s)
(s)
nel
dominio
ee(s)
e(s)
(di tensione
e di corrente)
di Laplace
L [
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s) Se la tensione e la
e(t) =
Ve(s)F(s)
= V-1udi
Iu(s) funzione
Funzione
eccitazione
o corrente)
u(t) = L
[(s)U(s)
] Ve(s)Y(s) =(tensione
F(s)
di rete
]
F(s) funzione
di rete
corrente si riferiscono
funzione di trasferimento
ammettenza di
alla stessa coppia di
ingresso
inIn
tensione
trasferimento
un
circuito
deve
essere
Un
circuito
privo
di generatori
Si suppone che E(s) sia l’unica eccitazione presente
morsetti, le impedenze
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s)
dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
Ie(s)Z(s)
=
V
(s)
(s)F(s)
=
I
(s)
e
le ammettenze
u diversa da ezero
di eccitazione
inizialiututte nulle rimane
a riposo
E(s) eimpedenza
U(s) sonoditrasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
sono dette
Iingresso
generatori controllati non in
danno
luogo a funzioni di eccitazione
trasferimento
corrente
ingresso
F(s)qualunque
non
è una trasformata
di elettrica
Laplace
grandezza
d’interesse deldi circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
Funzioni di rete
Esempio
Dominio del tempo
Vu +
Generatori indipendenti
+
+
R
R
circuito
e(t)
u(t)
(di
tensione e di corrente)
V
Vu
Iee
nel dominio
sL
Condizioni
del tempoiniziali
(su induttori e condensatori)
sL Ie di
= VLaplace
u
Dominio
sL
impedenza di trasferimento
(R+sL) Ie = Vu
V
IU(s)
(s)
circuito
IE(s)
V
(s)
(s)
uu(s)
di
ingresso
eGeneratori
eeR+sL impedenza
indipendenti
VIV
IE(s)
(s)Z(s)
F(s)
Y(s)
===VV
IU(s)
Iuu(s)
(s)
nel
dominio
ee(s)
e(s)
sL/(R+sL)
Ve =
Vu
(di
tensione
e
di
corrente)
di
Laplace
sL/(R+sL) funzione di trasferimento
L [
in tensione
Classificazione
funzioni
di
rete E(s) F(s) = U(s)
1
e(t) = L -1delle
[ E(s)
]
E(s) Se la tensione e la
e(t) =
Ve(s)F(s)
= V-1udi
Iu(s) funzione
Funzione
eccitazione
o corrente)
u(t) = L
[(s)U(s)
] Ve(s)Y(s) =(tensione
F(s)
di rete
]
F(s) funzione
di rete
corrente si riferiscono
funzione di trasferimento
ammettenza di
alla stessa coppia di
ingresso
inIn
tensione
trasferimento
un
circuito
deve
essere
Un
circuito
privo
di generatori
Si suppone che E(s) sia l’unica eccitazione presente
morsetti, le impedenze
presente dal
almeno
una funzione
indipendenti
e con
condizioni
F(s)
dipende
circuito
e Idalla
coppia
eccitazione
/ risposta
Ie(s)Z(s)
=
V
(s)
(s)F(s)
=
I
(s)
e
le ammettenze
u diversa da ezero
di eccitazione
inizialiututte nulle rimane
a riposo
E(s) eimpedenza
U(s) sonoditrasformate
di Laplace
di e(t) e u(t), rispettivamente
funzione
di trasferimento
sono dette
Iingresso
generatori controllati non in
danno
luogo a funzioni di eccitazione
trasferimento
corrente
ingresso
F(s)qualunque
non
è una trasformata
di elettrica
Laplace
grandezza
d’interesse deldi circuito
1
u(t) =L [ U(s) ]
Risposta (tensione o corrente)
38
M. Salerno
Tor Vergata
Laplace
39
Risposta impulsiva
Dominio del tempo
ue(t)
0(t)
circuito
nel dominio
del tempo
Dominio di Laplace
u(t)
h(t)
E(s)
1
1
e(t) = L [ 1 ]= u (t)
0
u(t) = h(t) : risposta impulsiva
1
h(t) = L [ F(s) ]
E(s) F(s) = U(s)
U(s)
F(s)
se E(s) = 1
F(s) = U(s)
la risposta impulsiva è
l’antitrasformata della
funzione di rete
M. Salerno
Tor Vergata
Laplace
39
Risposta impulsiva
Dominio del tempo
ue(t)
0(t)
circuito
e(t)
h(t) = u(t)
nel∗ dominio
del tempo
u(t)
h(t)
L [ ]
Dominio di Laplace
E(s)
1
E(s) F(s) = U(s)
prodotto di convoluzione
1
e(t) e(t)
= ∗ h(t) =1u(t)= u0(t) relazione diretta
fra e(t), h(t), u(t)
u(t)∞ = h(t) : risposta impulsiva
∫
1
∞
h(t) = L [ F(s) ]
e(t-τ ) h(τ ) d τ = u(t)
∫
e(τ ) h(t-τ ) d τ = u(t)
0-
0-
U(s)
F(s)
F(s)==1U(s)
seE(s)
E(s)
[E(s)]
e(t)
= L=-1U(s)
F(s)
h(t) = L -1[F(s)]
il prodotto di
la risposta impulsiva-1 è
convoluzione è
[U(s)]
u(t) = L
l’antitrasformata
della
commutativo
funzione di rete
M. Salerno
Tor Vergata
Laplace
40
Risposta impulsiva
La risposta impulsiva h(t) caratterizza il circuito nel dominio del tempo e
può essere rilevata sperimentalmente
Da h(t) si può determinare la funzione di rete F(s) :
Circuito in regime impulsivo
e(t)
u(t) = h(t) per e(t) = u0 (t)
e(t)
approssimante
di u0 (t)
δ
t
e(t) forma d’onda generica
=
/ 0 per 0 < t < δ
e(t) ∗ h(t) = u(t)
∞
∫0
F(s) = L[h(t)]
u(t) = e(τ ) h(t-τ ) d τ =
-
u(t)
δ
∫0e(τ ) h(t-τ ) d τ =
Ipotesi: δ tale che h(t-τ) ≅ h(t)
pper ogni
g t e pper 0 <τ <δ
δ
∫0
= e(τ ) h(t) d τ =
δ
∫0
h(t) e(τ ) d τ
M. Salerno
Tor Vergata
Laplace
40
Risposta impulsiva
La risposta impulsiva h(t) caratterizza il circuito nel dominio del tempo e
può essere rilevata sperimentalmente
Da h(t) si può determinare la funzione di rete F(s) :
Circuito in regime impulsivo
e(t)
u(t) = h(t) per e(t) = u0 (t)
e(t)
approssimante
di u0 (t)
A
δ
t
e(t) forma d’onda generica
=
/ 0 per 0 < t < δ
∫
δ
e(t) ∗ h(t) = u(t)
∞
∫0
F(s) = L[h(t)]
u(t) = e(τ ) h(t-τ ) d τ =
-
u(t)
δ
∫0e(τ ) h(t-τ ) d τ =
Ipotesi: δ tale che h(t-τ) ≅ h(t)
pper ogni
g t e pper 0 <τ <δ
∫
δ
= e(τ ) h(t) d τ =
∫
δ
h(t) e(τ ) d τ = A h(t)
A = e(τ ) d τ
0
0
0
La risposta u(t) è pari alla risposta impulsiva h(t), moltiplicata per l’area A della forma
d’onda d’ingresso [A in Volt sec]
M. Salerno
Tor Vergata
Laplace
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
h(t)
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare luogo a più risposte impulsive
in funzione della coppia eccitazione - risposta.
Un circuito è stabile, se lo è rispetto a tutte le
possibili risposte impulsive
41
M. Salerno
Tor Vergata
Laplace
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
a piùnegativo
risposte impulsive
polo
reale
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice: s = -a
-a
poli
x
Un circuito è stabile, se lo è rispetto a tutte le
possibili risposte impulsive
fattore di D(s): (s+a)
σ = Re[s]
t
andamento stabile
41
M. Salerno
Tor Vergata
Laplace
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
a piùnegativo
risposte impulsive
polo
reale
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice: s = -a
multiplo:
xx
-a
poli
Un circuito è stabile, se lo è rispetto a tutte le
possibili risposte impulsive
fattore di D(s): (s+a)n
σ = Re[s]
t
andamento stabile
41
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
poli
x-d
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
negativo
semplici
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice: sconiugati
multiplo:
complessi
= -a
con
xd
xx -c
-a
circuito stabile
Un circuito è stabile, se lo è rispetto a tutte le
parte
negativa:
possibili risposte impulsive
fattorereale
di D(s):
(s+a)n
σ = Re[s]
t
s = -c + jd
fattori di D(s): (s+c jd)
andamento stabileandamento stabile
+
Tor Vergata
Laplace
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
poli
xx
-d
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
negativo
semplici
multipli
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice: sconiugati
multiplo:
complessi
= -a
con
xxd
xx -c
-a
circuito stabile
Un circuito è stabile, se lo è rispetto a tutte le
parte
negativa:
possibili risposte impulsive
fattorereale
di D(s):
(s+a)n
σ = Re[s]
t
s = -c + jd
fattori di D(s): (s+c jd)n
andamento stabileandamento stabile
+
Tor Vergata
Laplace
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
poli
xx
-d
regione di stabilità
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
negativo
semplici
multipli
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice: sconiugati
multiplo:
complessi
= -a
con
xxd
xx -c
-a
circuito stabile
Un circuito è stabile, se lo è rispetto a tutte le
parte
negativa:
possibili risposte impulsive
fattorereale
di D(s):
(s+a)n
σ = Re[s]
t
s = -c + jd
fattori di D(s): (s+c jd)n
+
Tor Vergata
Laplace
andamento stabileandamento stabile
semipiano sinistro del piano s
Re[s] < 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
poli
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
coppia
polo
reale
poli
semplice
negativo
semplici
multipli
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
complessi
multiplo
sconiugati
= parte
-a
reale
con
xxd
xx -c
-a
circuito stabile
α
xσ = Re[s]
xx
-d
regione di stabilità
Un circuito è stabile, se lo è rispetto a tutte le
parte
negativa:
positiva:
s =(s+a)
α n
possibili risposte impulsive
fattorereale
di D(s):
t
forma
d’onda
andamento
illimitata
s = -c + jd
fattori
fattore di
di D(s):
D(s): (s+c
(s-α )njd)n
+
Tor Vergata
Laplace
stabileandamento
andamento
stabile
instabile
semipiano sinistro del piano s
Re[s] < 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
ω = Im[s]
xxd β
xx -c
-a
poli
h(t)
xx −β
-d
x
α γ
xσ = Re[s]
x
regione di stabilità
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
semplice
negativo
semplici
multipli
complessi
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
complessi
multiplo
coniugati,
sconiugati
semplici
= parte
-a
reale
ocon
Un circuito è stabile, se lo è rispetto a tutte le
parte
multipli,
negativa:
parte
n
positiva:
s =(s+a)
α reale
possibili risposte impulsive
fattorereale
dicon
D(s):
t
forma d’onda
andamento
illimitata
positiva: s = αs += j-cβ + jd
fattori
fattore di
di D(s):
D(s): (s+c
(s(s-α
γ )njd)
jβ n)n
++
Tor Vergata
Laplace
stabileandamento
andamento
stabile
instabile
semipiano sinistro del piano s
Re[s] < 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
xxd β
xx -c
-a
xx −β
-d
x
α γ
xσ = Re[s]
x
poli stabilità instabilità
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
semplice
negativo
semplici
multipli
complessi
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
complessi
multiplo
coniugati,
sconiugati
semplici
= parte
-a
reale
ocon
Un circuito è stabile, se lo è rispetto a tutte le
parte
multipli,
negativa:
parte
n
positiva:
s =(s+a)
α reale
possibili risposte impulsive
fattorereale
dicon
D(s):
t
forma d’onda
andamento
illimitata
positiva: s = αs += j-cβ + jd
fattori
fattore di
di D(s):
D(s): (s+c
(s(s-α
γ )njd)
jβ n)n
++
Tor Vergata
Laplace
stabileandamento
andamento
stabile
instabile
regione di stabilità semipiano sinistro del piano s
regione di instabilità semipiano destro del piano s
Re[s] < 0
Re[s] > 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
xxbdxβ
xx -c
-a
xx-b x−β
-d
x
α γ
xσ = Re[s]
x
poli stabilità instabilità
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
semplice
negativo
semplici
multipli
complessi
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
complessi
multiplo
coniugati,
coniugati
ssemplici,
coniugati
semplici
= parte
-a
reale
ocon
Un circuito è stabile, se lo è rispetto a tutte le
parte
multipli,
sull’asse
con
negativa:
parte
n
positiva:
s =(s+a)
α reale
possibili risposte impulsive
fattorereale
diimmaginario:
D(s):
t
forma
d’onda
forma
d’onda
andamento
illimitata
limitata
positiva: s =
s =+ αjsb+= j-cβ + jd
fattori
(s2+b
fattore di
di D(s):
D(s): (s+c
(s(sα
γ )2n)jd)
jβ n)n
++
Tor Vergata
Laplace
stabile
andamento
andamento
stabile
instabile
andamento
al limite
di stabilità
regione di stabilità semipiano sinistro del piano s
regione di instabilità semipiano destro del piano s
Re[s] < 0
Re[s] > 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
xxbdxβ
xx -c
-a
xx-b x−β
-d
x
α γ
xσ = Re[s]
x
poli stabilità instabilità
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
semplice
negativo
semplici
multipli
complessi
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
complessi
multiplo
coniugati,
coniugati
ssemplici,
coniugati
semplici
= parte
-a
reale
ocon
Un circuito è stabile, se lo è rispetto a tutte le
parte
multipli,
sull’asse
con
negativa:
parte
n
positiva:
s =(s+a)
α reale
possibili risposte impulsive
fattorereale
diimmaginario:
D(s):
t
forma
d’onda
forma
d’onda
andamento
illimitata
limitata
positiva: s =
s =+ αjsb+= j-cβ + jd
fattori
(s2+b
fattore di
di D(s):
D(s): (s+c
(s(sα
γ )2n)jd)
jβ n)n
++
Tor Vergata
Laplace
stabile
andamento
andamento
stabile
instabile
andamento
al limite
di stabilità
regione di stabilità semipiano sinistro del piano s
regione di instabilità semipiano destro del piano s
limite di stabilità
asse immaginario del piano s
Re[s] < 0
Re[s] > 0
Re[s] = 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
xxbdxβ
xx -c
-a
xx-b x−β
-d
x
α γ
xσ = Re[s]
x
poli stabilità instabilità
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
semplice
negativo
semplici
multipli
multipli,
complessi
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
multiplo
coniugati,
coniugati
complessi
ssemplici,
coniugati,
coniugati
semplici
= parte
-a
reale
ocon
Un circuito è stabile, se lo è rispetto a tutte le
parte
multipli,
sull’asse
con
negativa:
parte
n
positiva:
s =(s+a)
α reale
possibili risposte impulsive
fattorereale
diimmaginario:
D(s):
t
forma
d’onda
forma
d’onda
andamento
illimitata
limitata
illimitata
positiva: s =
s =+ αjsb+= j-cβ + jd
n
fattori
(s2+b
fattore di
di D(s):
D(s): (s+c
(s(sα
γ )2n)jd)
jβ n)n
++
Tor Vergata
Laplace
stabile
andamento
andamento
andamento
stabile
instabile
instabile
andamento
al limite
di stabilità
regione di stabilità semipiano sinistro del piano s
regione di instabilità semipiano destro del piano s
limite di stabilità
asse immaginario del piano s
Re[s] < 0
Re[s] > 0
Re[s] = 0
M. Salerno
41
Stabilità
u0(t)
e(t) ∗ h(t) = u(t)
piano s
h(t)
ω = Im[s]
xxbdxβ
xx -c
-a
xx-b x−β
-d
x
α γ
xσ = Re[s]
x
poli stabilità instabilità
circuito stabile
rispetto alla risposta
impulsiva h(t)
lim h(t) = 0
t
∞
Un circuito può dare
luogo
adi
più
risposte
impulsive
polo
coppia
reale
poli
semplice
negativo
semplici
multipli
multipli,
complessi
o
L[h(t)della
] coppia
F(s)in=funzione
eccitazione - risposta.
semplice:con
multiplo:
multiplo
coniugati,
coniugati
complessi
ssemplici,
coniugati,
coniugati
semplici
= parte
-a
reale
ocon
Un circuito è stabile, se lo è rispetto a tutte le
parte
multipli,
sull’asse
con
negativa:
parte
n
positiva:
s =(s+a)
α reale
possibili risposte impulsive
fattorereale
diimmaginario:
D(s):
t
forma
d’onda
forma
d’onda
andamento
illimitata
limitata
illimitata
positiva: s =
s =+ αjsb+= j-cβ + jd
n
fattori
(s2+b
fattore di
di D(s):
D(s): (s+c
(s(sα
γ )2n)jd)
jβ n)n
++
Tor Vergata
Laplace
stabile
andamento
andamento
andamento
stabile
instabile
instabile
andamento
al limite
di stabilità
regione di stabilità semipiano sinistro del piano s
regione di instabilità semipiano destro del piano s
limite di stabilità
asse immaginario del piano s
Re[s] < 0
Re[s] > 0
Re[s] = 0
poli
semplici
M. Salerno
Tor Vergata
Laplace
Stabilità dei circuiti
Circuiti reattivi
Componenti reattivi:
induttori, condensatori,
induttori accoppiati,
trasformatori ideali
Circuiti passivi
Componenti reattivi + resistori
Circuiti attivi
Componenti reattivi + resistori,
generatori controllati, nullori
F(s) = L[h(t)]
L’eccitazione, u0(t) , fornisce l’energia E al
circuito.
E non può né aumentare né diminuire. Le
risposte impulsive h(t) rimangono tutte
limitate, senza tendere a zero
E può diminuire. Le h(t) possono tendere a
zero, o rimanere limitate
E può aumentare. Le h(t) possono tendere a
zero, rimanere limitate o divergere
al limite di stabilità
poli per Re[s] = 0 semplici
stabile
poli per Re[s] < 0
poli per Re[s]=0 multipli
poli per Re[s]>0
instabile
{
42
M. Salerno
Laplace
43
Stabilità: esempi
Tor Vergata
+
sL
Circuito reattivo
Vu(s) Funzione di rete:
+
Ve(s)
funzione di trasferimento in tensione
1/sC
F(s) =
Vu(s)
1/sC
=
= 2 1
sL + 1/sC
s LC + 1
Ve(s)
Risposta impulsiva h(t) = L-1[F(s)]
1
1
1
ω0 = (LC)-1/2
F(s) = 2
=
2
2
s LC + 1 LC s + ω0
-1/2 j
F(s) = 2 Re[ A ] ; A = 1/LC
=
½
(LC)
s + jω0
s - jω0 s=- jω
0
h(t) = 2 Re[A e-jω0 t
] u-1(t)
Si ricordi che
F(s) =
piano s
ω = Im[s]
ω0 x
−ω0 x
poli
A + A* = 2 Re[ A ]
s + jω0 s - jω0
s + jω 0
σ = Re[s]
M. Salerno
Laplace
43
Stabilità: esempi
Tor Vergata
sL
+
Ve(s)
1/sC
Circuito reattivo
Vu(s) Funzione di rete:
+
funzione di trasferimento in tensione
F(s) =
Vu(s)
1/sC
=
= 2 1
sL + 1/sC
s LC + 1
Ve(s)
Risposta impulsiva h(t) = L-1[F(s)]
1
1
1
ω0 = (LC)-1/2
F(s) = 2
=
2
2
s LC + 1 LC s + ω0
-1/2 j
F(s) = 2 Re[ A ] ; A = 1/LC
=
½
(LC)
s + jω0
s - jω0 s=- jω
0
h(t) = 2 Re[A e-jω0 t
Si ricordi che
2 Re[A e-jω 0 t
]
] u-1(t) = (LC)-1/2 sin ω0 t
u-1(t)
piano s
ω = Im[s]
ω0 x
−ω0 x
σ = Re[s]
poli
A + A* = 2 Re[ A ]
F(s) =
s + jω0-1/2 j s(cos
- jωω
s +t)jω
-1/2 sin ω t
0 0 t - j sin ω
= 2 Re[½(LC)
0 ] 0= (LC)
0
M. Salerno
Laplace
43
Stabilità: esempi
Tor Vergata
sL
+
Ve(s)
1/sC
Circuito reattivo
Vu(s) Funzione di rete:
+
funzione di trasferimento in tensione
F(s) =
Vu(s)
1/sC
=
= 2 1
sL + 1/sC
s LC + 1
Ve(s)
Risposta impulsiva h(t) = L-1[F(s)]
1
1
1
ω0 = (LC)-1/2
F(s) = 2
=
2
2
s LC + 1 LC s + ω0
-1/2 j
F(s) = 2 Re[ A ] ; A = 1/LC
=
½
(LC)
s + jω0
s - jω0 s=- jω
0
h(t) = 2 Re[A e-jω0 t
h(t)
Si ricordi
che
2 Re[A e-jω 0 t
]
] u-1(t) = (LC)-1/2 sin ω0 t
u-1(t)
piano s
ω = Im[s]
ω0 x
−ω0 x
σ = Re[s]
poli
A + A* = 2 Re[ A ]
F(s) =
s + jω0-1/2 j s(cos
- jωω
s +t)jω
-1/2 sin ω t
0 t0 t - j sin ω
= 2 Re[½(LC)
0 ] 0= (LC)
0
andamento al limite di stabilità
M. Salerno
Laplace
43
Stabilità: esempi
Tor Vergata
+
sL
RL
Ve(s)
1/sC
Circuito reattivo
passivo
Ipotesi:
RdiL /rete:
L = 1/(CRC ) = D
Funzione
Vu(s)
L(s+ RL /L) in
=L(s+D)
sL
+ RL di= trasferimento
funzione
tensione= Lp
RC
sC + 1/R
c = C(s+ 1/CR
c )=C(s+D)1=Cp
Vu(s)
1/sC
F(s) =
=
= 2
sL
1/sC
s LC + 1
D +
reale
e positivo
VeD
p=s+
(s)
+
{
+ impulsiva
Nella variabile p, il
Risposta
h(t) = L-1[F(s)]+
pL
1
1
circuito è reattivo
Ve = 2 1
F(p)
= 1 2 1 2
1
V
u
ω0 L’analisi
= (LC)-1/2
F(s) = p2 LC + 1 = LC p2 + ω02
è identica
s LC + 1 LC s +1/pC
ω0
a quella del circuito
]
;
F(p) = 2 Re[ A
A
LC= ½ (LC)-1/2 j
F(s) = 2 Re[ p + jω0 ] ; A = 1/LC
s + jω0
s - jω0 s=- jω
Il0piano p è traslato
1/pC
1
a destra di D
F(p) =
=
-j
ω
t
-1/2
2
0 ] u-1
=+
(LC)
h(t) = 2 RepL
[A+e 1/pC
sin rispetto
ω0 t ual-1piano
(t) s
1
p(t)LC
h(t)
Si ricordi
che
2 Re[A e-jω 0 t
]
piano ps
ω = Im[p]
Im[s]
ω0 x
−ω0 x
poli
ξσ == Re[p]
Re[s]
ξ=σ+D
A + A* = 2 Re[ A ]
F(s) =
s + jω0-1/2 j s(cos
- jωω
s +t)jω
-1/2 sin ω t
0 t0 t - j sin ω
= 2 Re[½(LC)
0 ] 0= (LC)
0
andamento al limite di stabilità
M. Salerno
Laplace
43
Stabilità: esempi
Tor Vergata
+
RL
sL
Ve(s)
1/sC
Circuito reattivo
passivo
Ipotesi:
RdiL /rete:
L = 1/(CRC ) = D
Funzione
Vu(s)
L(s+ RL /L) in
=L(s+D)
sL
+ RL di= trasferimento
funzione
tensione= Lp
RC
sC + 1/R
c = C(s+ 1/CR
c )=C(s+D)1=Cp
Vu(s)
1/sC
F(s) =
=
= 2
sL
1/sC
s LC + 1
D +
reale
e positivo
VeD
p=s+
(s)
+
{
+ impulsiva
Nella variabile p, il
Risposta
h(t) = L-1[F(s)]+
pL
1
1
circuito è reattivo
Ve = 2 1
F(p)
= 1 2 1 2
1
V
u
ω0 L’analisi
= (LC)-1/2
F(s) = p2 LC1+ 1 = LC1 p2 +1ω02
è identica
+ 1 =LC s 2+1/pC
ω0 2
F(p) =s LC
2
p LC + 1 LC p + ω0
a quella del circuito
]
;
F(p) = 2 Re[ A
A
LC= ½ (LC)-1/2 j
F(s) = 2 Re[ p + Ajω0 ] ; A = 1/LC
1/LC
-1/2 j
F(p) = 2 Re[s + jω0 ] ; A =s - jω0 s=- jω
=
½
(LC)
Il
piano
p
è
traslato
p + jω
p - jω0 p=- jω0
1/pC 0
0
1
a destra
di D
F(p)
=
A
=
-j
ω
t
-1/2
2
F(s+D)
] =; +(LC)
0
h(t)
=2=
Re2pL
[Re
A+e[1/pC
sinin
ω0s t: -D
ual-1piano
1 poli
p(t)LC
+(t)jω0s
rispetto
-1
s+D ]+ ujω
0
piano ps
ω = Im[p]
Im[s]
ω0 x ω0 x
-D
−ω0 x−ω0 x
poli
σ
ξ == Re[p]
Re[s]
ξ=σ+D
h(t)
h(t)
= 2 Reche
[A e(-D-jω0 )t ] u-1(t)
Si ricordi
L’espressione è identica a quella del circuito LC, eccetto il
A + fattore
A* e-Dt= .2 Re[ A ]
F(s)
=
-D
t
-j
ω
t
= 2[Ae e-jωRe
t [A e 0 ] su+
ω
jω0-1/2 j s(cos
-Pertanto
jωω
dei poli
-1/2della
-1(t)
0 t0 lo
0= (LC)
0 ] = 2 Re[½(LC)
2 Re
t -spostamento
j sin ωs 0+at)jsinistra
]
sinquantità
ω0 t D
corrisponde allo smorzamento della risposta impulsiva
= (LC)-1/2 e-D t sin ω0 t u-1(t)
andamento al limite di stabilità
M. Salerno
Laplace
43
Stabilità: esempi
Tor Vergata
+
RL
sL
Ve(s)
1/sC
Circuito reattivo
passivo
Ipotesi:
RdiL /rete:
L = 1/(CRC ) = D
Funzione
Vu(s)
L(s+ RL /L) in
=L(s+D)
sL
+ RL di= trasferimento
funzione
tensione= Lp
RC
sC + 1/R
c = C(s+ 1/CR
c )=C(s+D)1=Cp
Vu(s)
1/sC
F(s) =
=
= 2
sL
1/sC
s LC + 1
D +
reale
e positivo
VeD
p=s+
(s)
+
{
+ impulsiva
Nella variabile p, il
Risposta
h(t) = L-1[F(s)]+
pL
1
1
circuito è reattivo
Ve = 2 1
F(p)
= 1 2 1 2
1
V
u
ω0 L’analisi
= (LC)-1/2
F(s) = p2 LC1+ 1 = LC1 p2 +1ω02
è identica
+ 1 =LC s 2+1/pC
ω0 2
F(p) =s LC
2
p LC + 1 LC p + ω0
a quella del circuito
]
;
F(p) = 2 Re[ A
A
LC= ½ (LC)-1/2 j
F(s) = 2 Re[ p + Ajω0 ] ; A = 1/LC
1/LC
-1/2 j
F(p) = 2 Re[s + jω0 ] ; A =s - jω0 s=- jω
=
½
(LC)
Il
piano
p
è
traslato
p + jω
p - jω0 p=- jω0
1/pC 0
0
1
a destra
di D
F(p)
=
A
=
-j
ω
t
-1/2
2
t 0sin] ωu-1pt(t)
-1/2
F(s+D)
]u=;-1+(t)
(LC)
h(t)
2=
Re2pL
[Re
A+
sinin
ω0s t: -D
ual-1piano
1/pC
1 poli
+(t)jω0s
rispetto
h(t)
== (LC)
ee[-D
s+D
+ j0ω0 LC
piano ps
ω = Im[p]
Im[s]
ω0 x ω0 x
-D
−ω0 x−ω0 x
poli
σ
ξ == Re[p]
Re[s]
ξ=σ+D
h(t)
h(t)
= 2 Reche
[A e(-D-jω0 )t ] u-1(t)
Si ricordi
L’espressione è identica a quella del circuito LC, eccetto il
A + fattore
A* e-Dt= .2 Re[ A ]
F(s)
=
-D
t
-j
ω
t
= 2[Ae e-jωRe
t [A e 0 ] su+
ω
jω0-1/2 j s(cos
-Pertanto
jωω
dei poli
-1/2della
-1(t)
0 t0 lo
0= (LC)
0 ] = 2 Re[½(LC)
2 Re
t -spostamento
j sin ωs 0+at)jsinistra
]
sinquantità
ω0 t D
corrisponde allo smorzamento della risposta impulsiva
= (LC)-1/2 e-D t sin ω0 t u-1(t)
andamento al
andamento
limite di stabilità
stabile
M. Salerno
Tor Vergata
Laplace
44
Stabilità: esempi
sL
I1
+
1/sC
8
I1
Ve
Circuito attivo
Funzione di rete:
funzione di trasferimento in tensione
+
I1 = Ve / sL
Vu
Vu = - (1/sC) I1
F(s) =
Risposta impulsiva h(t) = L-1[F(s)]; polo : s = 0, doppio
Vu(s))
= -1/(s2LC)
Ve(s))
piano s
ω = Im[p]
h(t) = L-1[F(s)] = L-1[-1/(s2LC)] = (-1/LC) u-2(t)
h(t)
rampa
xx
andamento
t
instabile
σ = Re[p]
poli
Il polo doppio all’origine (s = 0) dà luogo ad andamento instabile. Dal punto di vista della
stabilità, l’origine del piano s ha le stesse proprietà degli altri punti dell’asse immaginario
M. Salerno
Tor Vergata
Laplace
44
Stabilità: esempi
sL
I1
+
1/sC
8
I1
Ve
Circuito attivo
Funzione di rete:
funzione di trasferimento in tensione
+
I1 = Ve / sL
Vu
Vu = - (1/sC) I1
F(s) =
Risposta impulsiva h(t) = L-1[F(s)]; polo : s = 0, doppio
Vu(s))
= -1/(s2LC)
Ve(s))
piano s
ω = Im[p]
h(t) = L-1[F(s)] = L-1[-1/(s2LC)] = (-1/LC) u-2(t)
h(t)
rampa
xx
andamento
t
instabile
σ = Re[p]
poli
Il polol’applicazione
doppio all’origine
(s = 0)una
dà corrente
luogo adcostante
andamento
instabile.
Dal punto
di vista della
Dopo
dell’impulso,
percorre
l’induttore
e, proseguendo
nel
condensatore,
lo carica
L’energia
corrispondente
fornita
dal noratore.
stabilità, l’origine
del indefinitamente.
piano s ha le stesse
proprietà
degli altri èpunti
dell’asse
immaginario
M. Salerno
Tor Vergata
Laplace
45
Regime permanente
E(s)
E(s) F(s) = U(s)
E(s) = ½
E
s - jω
[
U(s) Ipotesi
{
e(t) = L-1[E(s)] = E cos(ω t + ϕ ) u-1(t )
circuito stabile
E*
+ s + jω ]
U(s) = ½
[
E
s - jω
E*
+ s + jω ]F(s)
Poli di U(s) : Poli di E(s) : per s = + jω + Poli di F(s) : per Re [s ] < 0
U(s) =
Up(s)
+
Ut (s)
Sviluppo
in frazioni
parziali
u(t) =
Si ricordi che:
E = E e jϕ
fasore di e(t)
sviluppo sui poli di E(s)
up(t)
+
sviluppo sui poli di F(s)
ut (t)
andamento sinusoidale permanente tende a zero per la stabilità: transitorio
E(s) = L[e(t)] = L[E cos(ω t + ϕ ) u-1(t )] =
= L[½[E e
jω t +
E*
] u-1(t )] = ½ [
e- j ω t
E
s - jω
+
E*
s + jω
]
M. Salerno
Tor Vergata
Laplace
45
Regime permanente
E(s)
E(s) F(s) = U(s)
E(s) = ½
[
E
s - jω
U(s) Ipotesi
{
e(t) = L-1[E(s)] = E cos(ω t + ϕ ) u-1(t )
circuito stabile
E*
+ s + jω ]
U(s) = ½
[
E
s - jω
E*
+ s + jω ]F(s)
Poli di U(s) : Poli di E(s) : per s = + jω + Poli di F(s) : per Re [s ] < 0
U(s) =
Up(s)
+
Ut (s)
Sviluppo
in frazioni
parziali
u(t) =
sviluppo sui poli di E(s)
up(t)
+
sviluppo sui poli di F(s)
ut (t)
andamento sinusoidale permanente tende a zero per la stabilità: transitorio
Calcolo
di che:
Up(s)
Si ricordi
½ U = U(s)(s – jω )|s=jω =
L[e(t)] = L[E cos(ω t + ϕ ) u-1(t )] =
U E(s) =U*
E
E*
jϕ [
U
+
]
Ep(s)
= E=e½
[ s - jω + s + jωE ](s – jω )E*
|s=jω
s - jω
s + jω jω t = ½ F(s)
j
ω
t
= L[½[E e + E* e ] u-1(t )] = ½ [
+ s + jω ]
fasore di e(t)
s
j
ω
U = F( jω ) E
= ½ F( jω ) E
M. Salerno
Tor Vergata
Laplace
46
Regime permanente
E(s)
E(s) F(s) = U(s)
U(s)
Laplace
Regime
permanente
E
E F(s)|s=jω = U
U
Circuito stabile: al crescere di t , tutte le risposte impulsive tendono a zero
tutte le risposte transitorie tendono a zero
tutte le grandezze elettriche del circuito
sono in regime sinusoidale permanente
Analisi nel dominio di Laplace
Analisi in regime permanente
Grandezze elettriche:
L-trasformate di tensioni e correnti
Grandezze elettriche:
fasori di tensioni e correnti
Funzioni di rete F(s)
Funzioni di rete F(s), con s = jω
La sostituzione s = jω può essere effettuata
in qualunque punto del procedimento
M. Salerno
Tor Vergata
Laplace
46
Regime permanente
E(s)
E(s) F(s) = U(s)
U(s)
Laplace
Regime
permanente
E
E F(s)|s=jω = U
U
Se jω è un polo di F(s), la suddivisione della risposta in
Circuito al
stabile:
limite alpermanente
crescere di t , tutte le risposte impulsive tendono a zero
e transitorio non può essere effettuata
di stabilità
Al crescere di t , alcune risposte impulsive non tendono a zero, ma
p.es. circuiti reattivi
F( jω) =/
∞
tutte le risposte transitorie tendono a zero
rimangono limitate
L’analisi in regime
permanente
può essere
effettata,
alcune
tutte
le grandezze
elettriche
delma
circuito
risposte transitorie di tipo sinusoidale si sovrappongono alle
sono in regime sinusoidale permanente
sinusoidi del regime permanente
Analisi nel dominio di Laplace
Analisi in regime permanente
Grandezze elettriche:
L-trasformate di tensioni e correnti
Grandezze elettriche:
fasori di tensioni e correnti
Funzioni di rete F(s)
Funzioni di rete F(s), con s = jω
La sostituzione s = jω può essere effettuata
in qualunque punto del procedimento
M. Salerno
Tor Vergata
Laplace
46
Regime permanente
E(s)
E(s) F(s) = U(s)
U(s)
Laplace
Regime
permanente
E
E F(s)|s=jω = U
U
Al jcrescere
di t ,dialcune
risposte
impulsive
non
tendono
Se
ω è un polo
F(s), la
suddivisione
della
risposta
ina zero e
Circuito al
instabile
stabile:
limite alpermanente
crescere
di
t , tutte
le
risposte
impulsive
tendono
a zero
possono divergere
e transitorio non può essere effettuata
di stabilità
Al
crescere
t , alcune
risposte impulsive
non
tendono
a zero, ma
L’analisi
indi
regime
permanente
può essere
effettata
formalmente,
p.es. circuiti reattivi
F( jω) =/
∞
tutte le risposte transitorie tendono a zero
rimangono
limitate
ma
può perdere
di validità, perché alcune risposte transitorie
possono mascherare
il regime permanente
L’analisi
in regime
permanente
può essere
effettata,
alcune
tutte
le grandezze
elettriche
delma
circuito
risposte
di tipo
si sovrappongono
alle i
L’analisitransitorie
con il metodo
deisinusoidale
fasori non permette
di determinare
sono
in
regime
sinusoidale
permanente
sinusoidi
permanente
transitori,del
néregime
di verificare
la stabilità, o meno, del circuito
Analisi nel dominio di Laplace
Analisi in regime permanente
Grandezze elettriche:
L-trasformate di tensioni e correnti
Grandezze elettriche:
fasori di tensioni e correnti
Funzioni di rete F(s)
Funzioni di rete F(s), con s = jω
La sostituzione s = jω può essere effettuata
in qualunque punto del procedimento
M. Salerno
Laplace
47
Regime permanente: esempio
Tor Vergata
t=0
+
L
i(t)
V cos(ω t+ϕ )
i(t) = 0 | t < 0
V(s) = ½
R
dominio di t
[
V
s - jω
+
V*
s + jω
];
V = V e jϕ
M. Salerno
Laplace
Regime permanente: esempio
Tor Vergata
t=0
+
sL
L
I(s)
i(t)
V(s)
V cos(ω t+ϕ )
i(t) = 0 | t < 0
V(s) = ½
R
dominiodidit s
dominio
piano s
ω = Im[p]
ω
-R/L
x
−ω x
s = + jω
poli della
eccitazione
x
σ = Re[p]
[
V
s - jω
+
V*
s + jω
];
V = V e jϕ
(sL+R)I(s) = V(s)
V
V*
I(s) = ½ [ s - jω + s + jω ] 1
sL+R
1
funzione di rete:
F(s) =
ammettenza d’ingresso
sL+R
poli di I(s)
poli
47
s = -R/L
polo della
funzione di rete
circuito stabile
Sviluppo in frazioni parziali di I(s)
I
I*
A
I(s) = ½ [ s - jω + s + jω ] + s+R/L
permanente
transitorio
transit
½V
½ I = I(s)(s - jω )|s = jω = jω L+R
A = I(s)(s + R/L )|s = -R/L =
V
V*
1
[
+
]
=
2L -R/L - jω
-R/L + jω
M. Salerno
Laplace
Regime permanente: esempio
Tor Vergata
t=0
+
V
V
= - ReV*
[
IV(s)
= = ½ [ ;V A +
; ] V= =- Re[I
V e jϕ]
jω L+R s - jω
s + jωjω]L+R
sL
L
I(s)
i(t)
V(s)
V cos(ω t+ϕ )
i(t) = 0 | t < 0
(cos ϕ + j sin ϕ )(- jω L+R)
Re[
]
=
]=
V Re[
(sL+R)I(s)
=
V(s)
jω L+R
ω2 L2+R2
R cos ϕ V*
+ ω L sin ϕ1
V
=
V
I(s) = ½ [ s - jω + sω2+Lj2ω
+R]2 sL+R
A = - Re[I ] 1= 0 per R cos
ϕ + ωdiL rete:
sin ϕ = 0
funzione
F(s) =
tan ϕ = - R d’ingresso
/ωL
ammettenza
sL+R
V
R
dominiodidit s
dominio
poli di I(s)
piano s
ω = Im[p]
ω
-R/L
−ω x
s = + jω
poli della
eccitazione
x
x
poli
47
σ = Re[p]
s = -R/L
polo della
funzione di rete
circuito stabile
Sviluppo in frazioni parziali di I(s)
I
I*
A
I(s) = ½ [ s - jω + s + jω ] + s+R/L
permanente
transitorio
transit
½V
½ I = I(s)(s - jω )|s = jω = jω L+R
A = I(s)(s + R/L )|s = -R/L =
V
V*
1
[
+
]
=
2L -R/L - jω
-R/L + jω
M. Salerno
Laplace
47
Regime permanente: esempio
Tor Vergata
t=0
+
I(s)
i(t)
V(s)
V cos(ω t+ϕ )
i(t) = 0 | t < 0
V
V
= - ReV*
[
IV(s)
= = ½ [ ;V A +
; ] V= =- Re[I
V e jϕ]
jω L+R s - jω
s + jωjω]L+R
sL
L
(cos ϕ + j sin ϕ )(- jω L+R)
Re[
]
=
]=
V Re[
(sL+R)I(s)
=
V(s)
jω L+R
ω2 L2+R2
R cos ϕ V*
+ ω L sin ϕ1
V
=
V
I(s) = ½ [ s - jω + sω2+Lj2ω
+R]2 sL+R
A = - Re[I ] 1= 0 per R cos
ϕ + ωdiL rete:
sin ϕ = 0
funzione
F(s) =
tan ϕ = - R d’ingresso
/ωL
ammettenza
sL+R
V
R
dominiodidit s
dominio
Andamenti
poli di I(s) nel tempo
i(t) =s ip(t) +ωit=(t)Im[p]
piano
s = + jω
ip(t) = Re[I e jω t] u-1(t)
poli della
ω
(R/L)
t
x
i (t) = A e
u (t)
Sviluppo in frazioni parziali di I(s)
I
I*
A
I(s) = ½ [ s - jω + s + jω ] + s+R/L
permanente
transitorio
transit
I = V / ( jω L+R)
½V
½ I = I(s)(s - jω )|s = jω = jω L+R
x
R cos ϕ + ω L sin ϕ
All’istante 0σ+= Re[p] s = -R/L
= - Re[I ]
A
=
V
x
A
=
I(s)(s
+
R/L
)
|
=
2
2
2
+
+
s = -R/L
ω L +R
I ] della
it(0 ) =−ω
A ; ip(0 ) = Re[polo
V
V*
1
funzione di rete
[
+
=
poli
i(0+) = A + Re[I ] = 0 circuito stabile A = - Re[I
= 0 - per
ϕ =+- jRω/]ω L
2L ]-R/L
jω tan-R/L
-R/L
t
eccitazione
-1
M. Salerno
Laplace
Regime permanente: esempio
Tor Vergata
t=0
sL
L
V
V
= - ReV*
[
IV(s)
= = ½ [ ;V A +
; ] V= =- Re[I
V e jϕ]
jω L+R s - jω
s + jωjω]L+R
i(t)
(cos ϕ + j sin ϕ )(- jω L+R)
Re[
]
=
]=
V Re[
(sL+R)I(s)
=
V(s)
jω L+R
ω2 L2+R2
R
R cos ϕ V*
+ ω L sin ϕ1
V
=
V
t
I(s)] = ½ [ s - jω + sω2+Lj2ω
Re[I
+R]2 sL+R
A = - Re[I ] 1= 0 per R cos
ϕ + ωdiL rete:
sin ϕ = 0
funzione
F(s) =
tan ϕ = - R
/ωL
ammettenza
d’ingresso
sL+R
permanente
i(t) = 0 | t < 0
dominiodidit s
dominio
Andamenti
Sviluppo in frazioni parziali di I(s)
poli di I(s) nel tempo
I
I*
A
i(t) =s ip(t) +ωit=(t)Im[p]
piano
I(s) = ½ [ s - jω + s + jω ] + s+R/L
s = + jω
ip(t) = Re[I e jω t] u-1(t)
permanente
transitorio
transit
poli
della
itω
(t)x= A e - (R/L) t ueccitazione
I = V / ( jω L+R)
½V
-1(t)
-R/L
½ I = I(s)(s - jω )|s = jω = jω L+R
x
R cos ϕ + ω L sin ϕ
All’istante 0σ+= Re[p] s = -R/L
= - Re[I ]
A
=
V
x
A
=
I(s)(s
+
R/L
)
|
=
2
2
2
+
+
s = -R/L
ω L +R
I ] della
it(0 ) =−ω
A ; ip(0 ) = Re[polo
V
V*
1
funzione di rete
[
+
=
poli
i(0+) = A + Re[I ] = 0 circuito stabile A = - Re[I
= 0 - per
ϕ =+- jRω/]ω L
2L ]-R/L
jω tan-R/L
+
I(s)
i(t)
V(s)
V cos(ω t+ϕ )
V
47
M. Salerno
Laplace
Regime permanente: esempio
Tor Vergata
t=0
sL
L
V
V
= - ReV*
[
IV(s)
= = ½ [ ;V A +
; ] V= =- Re[I
V e jϕ]
jω L+R s - jω
ω]L+R
s + jωjtransitorio
i(t)
(cos ϕ + j sin ϕ )(- jω L+R)
Re[
]
=
]=
V Re[
(sL+R)I(s)
=
V(s)
2 L2+R2
j
ω
L+R
ω
A
R
R cos ϕ V*
+ ω L sin ϕ1
V
=
V
t
I(s)] = ½ [ s - jω + sω2+Lj2ω
Re[I
+R]2 sL+R
A = - Re[I ] 1= 0 per R cos
ϕ + ωdiL rete:
sin ϕ = 0
funzione
F(s) =
tan ϕ = - R
/ωL
ammettenza
d’ingresso
sL+R
permanente
i(t) = 0 | t < 0
dominiodidit s
dominio
Andamenti
Sviluppo in frazioni parziali di I(s)
poli di I(s) nel tempo
I
I*
A
i(t) =s ip(t) +ωit=(t)Im[p]
piano
I(s) = ½ [ s - jω + s + jω ] + s+R/L
s = + jω
ip(t) = Re[I e jω t] u-1(t)
permanente
transitorio
transit
poli
della
itω
(t)x= A e - (R/L) t ueccitazione
I = V / ( jω L+R)
½V
-1(t)
-R/L
½ I = I(s)(s - jω )|s = jω = jω L+R
x
R cos ϕ + ω L sin ϕ
All’istante 0σ+= Re[p] s = -R/L
= - Re[I ]
A
=
V
x
A
=
I(s)(s
+
R/L
)
|
=
2
2
2
+
+
s = -R/L
ω L +R
I ] della
it(0 ) =−ω
A ; ip(0 ) = Re[polo
V
V*
1
funzione di rete
[
+
=
poli
i(0+) = A + Re[I ] = 0 circuito stabile A = - Re[I
= 0 - per
ϕ =+- jRω/]ω L
2L ]-R/L
jω tan-R/L
+
I(s)
i(t)
V(s)
V cos(ω t+ϕ )
V
47
M. Salerno
Laplace
Regime permanente: esempio
Tor Vergata
t=0
sL
L
V
risposta
completa
V
V
V*
= - Re[ transitorio
IV(s)
= = ½ [ ; A+
; ] V= =- Re[I
V e jϕ]
jω L+R s - jω
s + jωjω]L+R
i(t)
(cos ϕ + j sin ϕ )(- jω L+R)
Re[
]
=
]=
V Re[
(sL+R)I(s)
=
V(s)
2 L2+R2
j
ω
L+R
ω
A
R
R cos ϕ V*
+ ω L sin ϕ1
V
=
V
t
I(s)] = ½ [ s - jω + sω2+Lj2ω
Re[I
+R]2 sL+R
A = - Re[I ] 1= 0 per R cos
ϕ + ωdiL rete:
sin ϕ = 0
funzione
F(s) =
tan ϕ = - R
/ωL
ammettenza
d’ingresso
sL+R
permanente
i(t) = 0 | t < 0
dominiodidit s
dominio
Andamenti
Sviluppo in frazioni parziali di I(s)
poli di I(s) nel tempo
I
I*
A
i(t) =s ip(t) +ωit=(t)Im[p]
piano
I(s) = ½ [ s - jω + s + jω ] + s+R/L
s = + jω
ip(t) = Re[I e jω t] u-1(t)
permanente
transitorio
transit
poli
della
itω
(t)x= A e - (R/L) t ueccitazione
I = V / ( jω L+R)
½V
-1(t)
-R/L
½ I = I(s)(s - jω )|s = jω = jω L+R
x
R cos ϕ + ω L sin ϕ
All’istante 0σ+= Re[p] s = -R/L
= - Re[I ]
A
=
V
x
A
=
I(s)(s
+
R/L
)
|
=
2
2
2
+
+
s = -R/L
ω L +R
I ] della
it(0 ) =−ω
A ; ip(0 ) = Re[polo
V
V*
1
funzione di rete
[
+
=
poli
i(0+) = A + Re[I ] = 0 circuito stabile A = - Re[I
= 0 - per
ϕ =+- jRω/]ω L
2L ]-R/L
jω tan-R/L
+
I(s)
i(t)
V(s)
V cos(ω t+ϕ )
V
47
M. Salerno
Laplace
Regime permanente: esempio
Tor Vergata
t=0
sL
L
V
risposta
completa
V
V
V*
= - Re[ transitorio
IV(s)
= = ½ [ ; A+
; ] V= =- Re[I
V e jϕ]
jω L+R s - jω
s + jωjω]L+R
i(t)
(cos ϕ + j sin ϕ )(- jω L+R)
Re[
]
=
]=
V Re[
(sL+R)I(s)
=
V(s)
2 L2+R2
j
ω
L+R
ω
A
R
R cos ϕ V*
+ ω L sin ϕ1
V
=
V
t
I(s)] = ½ [ s - jω + sω2+Lj2ω
Re[I
+R]2 sL+R
A = - Re[I ] 1= 0 per R cos
ϕ + ωdiL rete:
sin ϕ = 0
funzione
F(s) =
tan ϕ = - R
/ωL
ammettenza
d’ingresso
sL+R
i(t) = 0 | t < 0
permanente
dominiodidit s
dominio
Andamenti
tempo
in frazioni
parzialididi
Il circuito
rilevante
in molte applicazioni, inSviluppo
quanto rappresenta
l’inserzione
unI(s)
carico
poli
di I(s)è nel
I
I*
induttivo
(p.+es.i (t)
un trasformatore, un motore, ecc.) su un generatore
sinusoidale
(p. es. A
la
i(t) =s ip(t)
piano
t
½
[
+
]
+
I(s)
=
ω = Im[p] di rete)
tensione di alimentazione
s+R/L
s - jω
s + jω
s = + jω
ip(t) = Re[I e jω t] u-1(t)
permanente
transitorio
transit
poli
della
Nelle applicazioni
tutti
i
parametri
sono
noti,
eccetto
l’angolo
ϕ
,
che
dipende
dall’istante
di
ω
(R/L)
t
x
it(t) in
= genere
A e casuale.
ueccitazione
= V / ( jωl’andamento
L+R)
½ Vcompleta
-1(t)
inserzione,
Risulta così nonIprevedibile
risposta
-R/L
½ I = I(s)(s
- jω )|s =della
=
jω
jω L+R
x
+
R
cos
ϕ
+
ω
L
sin
ϕ
0σ = Re[p]
s = -R/L
IlAll’istante
caso più favorevole
si ha quando
il transitorio
è=assente
(A = 0 ; tan ϕ = - R / ω L)=e -laRe[I ]
A
V
x; i (0+è)pari
A = I(s)(s + R/L
2 L)2|+R
s = 2-R/L =
corrente
massima
a |[polo
II| ]. della
ω
=
Re
it(0+) =−ω
A
p
V
V*
1
funzione di rete
[
+
=
Nel+caso
della corrente
diϕ 2=| +
I-| jR
poli
i(0
) = Apeggiore,
+ Re[Iil]valore
= 0 assoluto
A = può
- Re[I
]-R/L
= 0 - per
tan-R/L
circuito stabile
2Lraggiungere
jilωvalore
ω/]ω L
+
i(t)
I(s)
V(s)
V
cos(ω t+ϕ )
V
47
M. Salerno
Tor Vergata
Laplace
48
Risposta in frequenza
E(s)
U(s)
Laplace
E(s) F(s) = U(s)
Regime
permanente
E
U
E F(s)|s=jω = U
L’espressione U = F( jω) E può essere utilizzata per ottenere informazioni
sul comportamento della rete al variare della frequenza f = ω / 2π .
La funzione F(jω) = F( j 2π f ) è detta risposta in frequenza del circuito.
La frequenza è considerata come una variabile.
Nel calcolo della risposta in
frequenza si può determinare prima
F(s)
( in presenza del solo
generatore d’interesse
e condizioni iniziali nulle )
e poi porre s = jω ( = j 2π f )
La risposta in frequenza si può
anche calcolare
ponendo subito s = j ω , e poi
determinare direttamente F(jω) .
M. Salerno
Tor Vergata
Laplace
48
Risposta in frequenza
E(s)
U(s)
Laplace
E(s) F(s) = U(s)
Regime
permanente
E
U
E F(s)|s=jω = U
L’espressione U = F( jω) E può essere utilizzata per ottenere informazioni
sul comportamento della rete al variare della frequenza f = ω / 2π .
La funzione F(jω) = F( j 2π f ) è detta risposta in frequenza del circuito.
La frequenza è considerata come una variabile.
sL risposta in
Nel calcolo della
frequenza
+ si può determinare prima
+
F(s)
( in presenza del solo V
Vi
R
1/sC
u
generatore d’interesse
e condizioni iniziali nulle )
e poi porre s = jω ( = j 2π f ) s = j ω
Risposta in frequenza
La
frequenza
[ s risposta
C + (1/R)in
+ (1/sL)
] Vu =si( può
1/sL ) Vi
anche calcolare
1
=
V
V
u
ponendo
s2 Csubito
+ s L /sR=+j 1ω , ei poi
determinare direttamente F(jω) .
1
F (jω) =
-ω2 C + j ω L / R + 1
M. Salerno
Laplace
49
Risposta in ampiezza e fase
Tor Vergata
Risposta in frequenza
ω =2πf
F ( j ω ) = F (s) per s = j ω
Risposta di ampiezza: A ( ω ) = | F ( j ω ) |
Risposta di fase: β ( ω ) = Arg [ F ( j ω ) ]
10
R +
Vu(s)
sL
Vi(s)
1/sC
Dominio di Laplace
Per R = L = C = 1 : F (s) =
Attenuazione AdB
20
+
1
s2 + s + 1
Risposta in frequenza
F(jω)=
1
1 - ω2 + j ω
Risposta in ampiezza
A(ω)=
0
frequenza normalizzata
Attenuazione
1
[( 1 - ω 2 )2 + ω 2 ] ½
AdB (ω ) = - 20 log10 A (ω )
M. Salerno
Laplace
49
Risposta in ampiezza e fase
Tor Vergata
Risposta in frequenza
ω =2πf
F ( j ω ) = F (s) per s = j ω
Risposta di ampiezza: A ( ω ) = | F ( j ω ) |
-120
-60
0
Fase in gradiAdB
Attenuazione
Risposta di fase: β ( ω ) = Arg [ F ( j ω ) ]
Vi(s)
R +
Vu(s)
sL
1/sC
Dominio di Laplace
Per R = L = C = 1 : F (s) =
1
s2 + s + 1
Risposta in frequenza
20
F(jω)=
1
1 - ω2 + j ω
Risposta in ampiezza
fase
10
1
2
) =) = - A t g [ ω
Aβ
( ω( ω
[( 1 - ω 2 )/2 (+1ω- 2ω] ½)]
0
-180
+
frequenza normalizzata
La quantità β ( ω ) può essere
AdB (ω )in
= -radianti
20 log10o A
(ω )
Attenuazione
rappresentata
gradi
M. Salerno
Tor Vergata
Laplace
49
Risposta in ampiezza e fase
Risposta in frequenza
ω =2πf
F ( j ω ) = F (s) per s = j ω
Risposta di ampiezza: A ( ω ) = | F ( j ω ) |
-120
-60
0
Fase in gradiAdB
Attenuazione
Risposta di fase: β ( ω ) = Arg [ F ( j ω ) ]
Ritardo di gruppo
In molti casi, in luogo della risposta di fase,
si utilizza un’altra grandezza che
20rappresenta il ritardo del trasferimento del
segnale fra ingresso e uscita
Tale ritardo risulta funzione della
10frequenza e rappresenta il ritardo di un
inviluppo che modula il segnale
-180
0Si dimostra che:
τ ( ω ) = − dfrequenza
β ( ω ) / normalizzata
dω
+
Vi(s)
sL
R +
Vu(s)
1/sC
Dominio di Laplace
Per R = L = C = 1 : F (s) =
1
s2 + s + 1
Nel caso dell’esempio
si ha:
Risposta
in frequenza
1
τ ( ω ) = − d β (ω ) / d ω
F(jω)=
con β ( ω ) = - A t g [ ω1/ -( ω
1 2- +
ω 2j )ω]
Risposta
fase
τ (ω ) = din{ ampiezza
A t g [ω / (1 - ω 2 )]1} / d ω
2
) =) = - A t g [ ω
Aβ
( ω( ω
Si dimostra che:
[( 1 - ω 2 )/2 (+1ω- 2ω] ½)]
β ( -ωω) 2può
2) / [(1
2 +essere
τ
(ω ) = (La
1 +quantità
ω
)
ω(2ω])
A
(
ω
)
=
20
log
A
Attenuazione
rappresentata
in radianti10o gradi
dB
M. Salerno
Tor Vergata
Laplace
49
Risposta in ampiezza e fase
Risposta in frequenza
ω =2πf
F ( j ω ) = F (s) per s = j ω
Risposta di ampiezza: A ( ω ) = | F ( j ω ) |
-120
-60
0
tempo
Fasenormalizzato
in gradiAdB
Attenuazione
Risposta di fase: β ( ω ) = Arg [ F ( j ω ) ]
Ritardo di gruppo
2In molti casi, in luogo della risposta di fase,
si utilizza un’altra grandezza che
20rappresenta il ritardo del trasferimento del
segnale fra ingresso e uscita
Tale ritardo risulta funzione della
101frequenza e rappresenta il ritardo di un
inviluppo che modula il segnale
-180
0Si dimostra che:
frequenza normalizzata
τ ( ω ) = − dfrequenza
β ( ω ) / normalizzata
dω
0
+
Vi(s)
sL
R +
Vu(s)
1/sC
Dominio di Laplace
Per R = L = C = 1 : F (s) =
1
s2 + s + 1
Nel caso dell’esempio
si ha:
Risposta
in frequenza
1
τ ( ω ) = − d β (ω ) / d ω
F(jω)=
con β ( ω ) = - A t g [ ω1/ -( ω
1 2- +
ω 2j )ω]
Risposta
fase
τ (ω ) = din{ ampiezza
A t g [ω / (1 - ω 2 )]1} / d ω
2
) =) = - A t g [ ω
Aβ
( ω( ω
Si dimostra che:
[( 1 - ω 2 )/2 (+1ω- 2ω] ½)]
β ( -ωω) 2può
2) / [(1
2 +essere
τ
(ω ) = (La
1 +quantità
ω
)
ω(2ω])
A
(
ω
)
=
20
log
A
Attenuazione
rappresentata
in radianti10o gradi
dB
M. Salerno
Tor Vergata
Laplace
Normalizzazione
Circuito normalizzato
Modello di circuito reale, avente le funzioni di trasferimento desiderate
La gamma di frequenze è fittizia , p.es. nell’intorno della frequenza unitaria.
Le impedenze in uso sono fittizie , p.es in modulo di valore prossimo all’unità
Il circuito normalizzato è usato per semplificare l’analisi e il progetto di circuiti reali.
Il circuito normalizzato è universale,
nel senso che da esso si possono ottenere molti circuiti reali
Per il circuito normalizzato si considerano grandezze normalizzate, p. es. :
frequenza fN , tempo tN , valori dei componenti RN , LN , CN , ecc.
Denormalizzazione : il processo che permette di ottenere il circuito reale
dal circuito normalizzato
Per il circuito reale si hanno le usuali grandezze, p. es. :
frequenza f , tempo t , valori dei componenti R , L , C , ecc.
50
M. Salerno
Tor Vergata
Laplace
Normalizzazione
Circuito
normalizzato
Denormalizzazione
di frequenza
Denormalizzazione di livello
Data
una resistenzadesiderate
di
Data
una frequenza
di reale, avente le funzioni
Modello
di circuito
di trasferimento
f
=
f
f
Z = ZN r0
N 0
normalizzazione
r
normalizzazione
f
0
0
La gamma di frequenze
è fittizia , p.es. nell’intorno della frequenza unitaria.
Nel
normalizzato
e nel fittizie
circuito, p.es in modulo
Nel circuito
reale tutte
le impedenze
sono
Lecircuito
impedenze
in uso sono
di valore
prossimo
all’unità
reale tutte le impedenze e tutte le
uguali a quelle del circuito normalizzato
ammettenze
devono essere
le medesime
perdir0circuiti reali.
Il circuito
normalizzato
è usato
per semplificare l’analisimoltiplicate
e il progetto
IlEsempio:
circuito jnormalizzato
è universale,
2 π f L = j 2 π fN LN
Esempio: R = RN r0
nel senso che da esso si possono ottenere molti circuiti reali
Per il circuito normalizzato si considerano grandezze normalizzate, p. es. :
frequenza fN , tempo tN , valori dei componenti RN , LN , CN , ecc.
Denormalizzazione : il processo che permette di ottenere il circuito reale
dal circuito normalizzato
Per il circuito reale si hanno le usuali grandezze, p. es. :
frequenza f , tempo t , valori dei componenti R , L , C , ecc.
50
M. Salerno
Tor Vergata
Laplace
Normalizzazione
Circuito
normalizzato
Denormalizzazione
di frequenza
Denormalizzazione di livello
Data
una resistenzadesiderate
di
Data
una frequenza
di reale, avente le funzioni
Modello
di circuito
di trasferimento
f
=
f
f
Z = ZN r0
N 0
normalizzazione
r
normalizzazione
f
0
0
La gamma di frequenze
è fittizia , p.es. nell’intorno della frequenza unitaria.
Nel
circuito
Nel circuitof reale
sono
= fN tutte
; t =letNimpedenze
f = fN normalizzato
f0 ;int =uso
tN sono
/e fnel
Lecircuito
impedenze
prossimo
all’unità
0 fittizie , p.es in modulo di valore
reale tutte le impedenze e tutte le
uguali a quelle del circuito normalizzato
R = RN
R = RN r0
ammettenze
devono essere
le medesime
perdir0circuiti reali.
Il circuito
normalizzato
è usato
per semplificare l’analisimoltiplicate
e il progetto
L =normalizzato
LN / f0
L = LN r0
IlEsempio:
circuito
è
universale,
j 2 π f L = j 2 π fN LN
Esempio: R = RN r0
C
=
C
/
f
C = CN / r0
nel senso cheNda esso
si possono ottenere molti circuiti reali
0
Denormalizzazione
contemporanea
di frequenza
e di livello
Per il circuito normalizzato
si considerano
grandezze
normalizzate, p. es. :
Assegnate
la frequenza
di normalizzazione
f0
frequenza
fN , tempo
tN , valori dei componenti
RN , LN , CN , ecc.
e la resistenza di normalizzazione r0
Denormalizzazione
permette di ottenere il circuito reale
f = fN f:0 il ;processo
t = tN / fche
0
R = RN r0dal circuito normalizzato
Per il circuitoLreale
le usuali grandezze, p. es. :
= LNsi rhanno
0 / f0
frequenza f , tempo t , valori dei componenti R , L , C , ecc.
C = CN / ( f0 r0 )
50
M. Salerno
Tor Vergata
Laplace
Normalizzazione
Esempio
Circuito
normalizzato
Denormalizzazione
di frequenza
Denormalizzazione di livello
Data
una resistenzadesiderate
di
Data
una frequenza
di reale, avente le funzioni
Modello
di circuito
di trasferimento
f
=
f
f
Z = ZN r0
N 0
normalizzazione
r
normalizzazione
f
0
+
+
0
La gamma
di frequenze
è fittizia , p.es. nell’intorno
R = 750della
Ω ; frequenza unitaria.
R
circuito
Nel
circuito
f reale
= fN tutte
=letNimpedenze
f = fN normalizzato
f0 C;int =uso
tN sono
/e fnel
L=
750/1000
=; t750
mH
; sono
ViNel
L V, p.es
Lecircuito
impedenze
in modulo
di valore
prossimo
all’unità
0 fittizie
u
reale tutte le impedenze e tutte le
uguali a quelle del6 circuito normalizzato
C = 1 / R1.5= 10
R = RN
RN =
r0 0,67 µF
ammettenze
devono essere
le medesime
perdir0circuiti reali.
Il circuito
normalizzato
è usato
per semplificare l’analisimoltiplicate
e il progetto
L =normalizzato
LN / f0
L in
= LkHz
frequenze
N r0
IlEsempio:
circuito
è
universale,
j 2 ;πLf L == 1/2
j 2 π;fNCLN=1
Esempio:
R [=ms
RN ]r0
=
1/2
R
tempi
in
C
=
C
/
f
C
=
N
N
N
nel senso cheNda esso
si possono ottenere molti circuiti reali CN / r0
0
f0 = 1000 ; r0 = 1500
Denormalizzazione
contemporanea
di frequenza
e di livello
Per il circuito normalizzato
si considerano
grandezze
normalizzate, p. es. :
Assegnate
la frequenza
di normalizzazione
f0
frequenza
fN , tempo
tN , valori dei componenti
RN , LN , CN , ecc.
e la resistenza di normalizzazione r0
Denormalizzazione
permette di ottenere il circuito reale
f = fN f:0 il ;processo
t = tN / fche
0
R = RN r0dal circuito normalizzato
Per il circuitoLreale
le usuali grandezze, p. es. :
= LNsi rhanno
0 / f0
frequenza f , tempo t , valori dei componenti R , L , C , ecc.
C = CN / ( f0 r0 )
50