Statistica e informatica CTF
Esercizi di prova 1
Nome:
N. mat.:
:STINF391
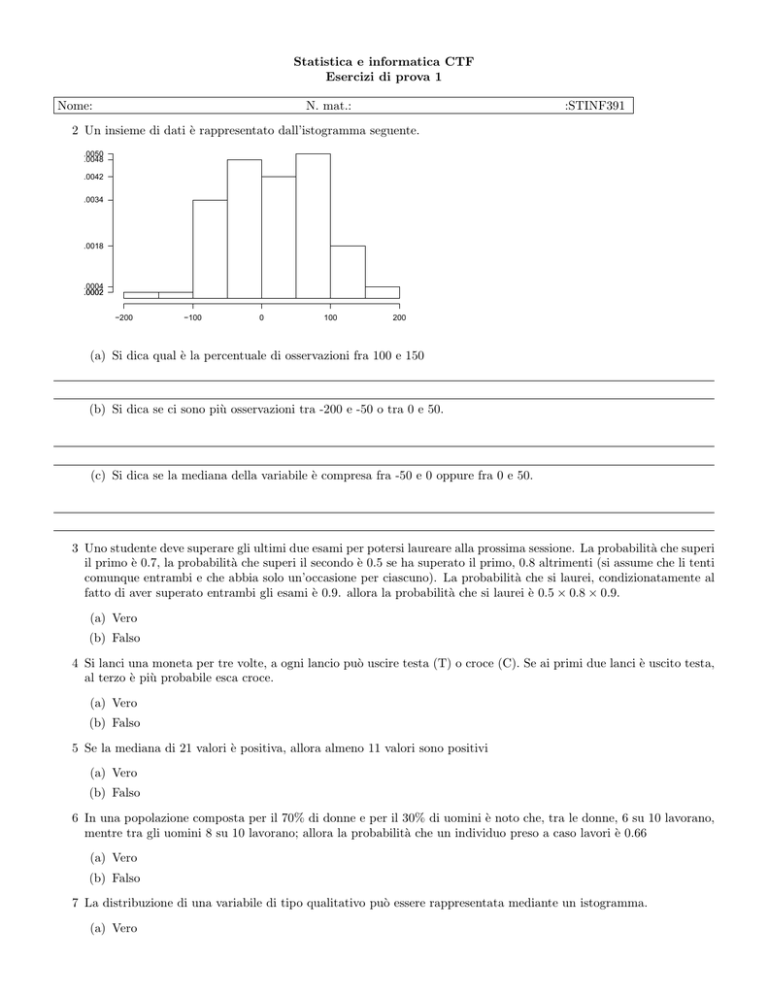
2 Un insieme di dati è rappresentato dall’istogramma seguente.
0.0050
0.0048
0.0042
0.0034
0.0018
0.0004
0.0002
−200
−100
0
100
200
(a) Si dica qual è la percentuale di osservazioni fra 100 e 150
(b) Si dica se ci sono più osservazioni tra -200 e -50 o tra 0 e 50.
(c) Si dica se la mediana della variabile è compresa fra -50 e 0 oppure fra 0 e 50.
3 Uno studente deve superare gli ultimi due esami per potersi laureare alla prossima sessione. La probabilità che superi
il primo è 0.7, la probabilità che superi il secondo è 0.5 se ha superato il primo, 0.8 altrimenti (si assume che li tenti
comunque entrambi e che abbia solo un’occasione per ciascuno). La probabilità che si laurei, condizionatamente al
fatto di aver superato entrambi gli esami è 0.9. allora la probabilità che si laurei è 0.5 × 0.8 × 0.9.
(a) Vero
(b) Falso
4 Si lanci una moneta per tre volte, a ogni lancio può uscire testa (T) o croce (C). Se ai primi due lanci è uscito testa,
al terzo è più probabile esca croce.
(a) Vero
(b) Falso
5 Se la mediana di 21 valori è positiva, allora almeno 11 valori sono positivi
(a) Vero
(b) Falso
6 In una popolazione composta per il 70% di donne e per il 30% di uomini è noto che, tra le donne, 6 su 10 lavorano,
mentre tra gli uomini 8 su 10 lavorano; allora la probabilità che un individuo preso a caso lavori è 0.66
(a) Vero
(b) Falso
7 La distribuzione di una variabile di tipo qualitativo può essere rappresentata mediante un istogramma.
(a) Vero
(b) Falso
8 Per confrontare l’efficacia di due farmaci (A e B) li si somministra a due gruppi di pazienti e si valuta per ciascuno
se si sia ottenuto un miglioramento. I risultati sono riportati nella tabella seguente.
A
B
Migl
368
199
Non migl
98
44
(a) Qual è la frequenza relativa dei pazienti che hanno avuto un miglioramento tra quelli che hanno ricevuto il
farmaco A?
(b) Se un trattamento col farmaco A costa 100 euro e un trattamento col farmaco B ne costa 200, qual ‘e stata la
spesa media per paziente?
9 Se tutti i valori di un data set sono incrementati di 20, sia la media che la mediana aumenteranno di 20.
(a) Vero
(b) Falso
10 Mario spedisce a Lucia un pacco che contiene un regalo di compleanno. È in programma però uno sciopero degli
spedizionieri. Mario ritiene che la probabilità che il pacco arrivi in tempo (prima del compleanno) è 0.8 se non ci
sarà lo sciopero programmato, 0.5 altrimenti. La probabilità che lo sciopero programmato si svolga effettivamente
vale 0.5, la probabilità che il pacco arrivi in tempo è quindi 0.5.
(a) Vero
(b) Falso
11 Se due eventi sono indipendenti allora P (A|B) = P (B|A).
(a) Vero
(b) Falso
12 Lo scarto quadratico medio è
(a) la media dei quadrati degli scarti dalla media aritmetica
(b) la radice quadrata della varianza
(c) la radice quadrata della media dei valori al quadrato
13 La mediana è sempre maggiore della media.
(a) Vero
(b) Falso
14 Si lanci una moneta per tre volte, a ogni lancio può uscire testa (T) o croce (C). È più probabile osservare due teste
e una croce che tre teste.
(a) Vero
(b) Falso
15 In un diagramma a scatola il baffo superiore rappresenta il 75o percentile.
(a) Vero
(b) Falso
16 Un insieme di dati è rappresentato dal boxplot seguente.
−4.4
−4.2
−4.0
−3.8
−3.6
(a) Si dica quanto vale la mediana dell’insieme di dati
Si dica quali sono il più piccolo e il più grande valore osservato.
(b) Quanto vale lo scarto interquartile?
17 Alle ultime elezioni regionali del Veneto è anadato a votare il 57% degli elettori. Alle precedenti reginali Venete
aveva votato il 66%. Quale delle seguenti affermazioni è vera:
(a) La proporzione di votanti è calata del 9%
(b) La proporzione di votanti è calata di quasi il 14%
(c) La proporzione di votanti è calata quasi del 16%











