Livelli energetici (discreti)
Atomo d’idrogeno
Orbitali elettronici
In generale 3 numeri quantici
descrivono la funzione d’onda
dell’elettrone:
– n=1,2,3,…... K,L,M,N,….. shell
– l= 0,1,2,….,n-1 s,p,d,f,….. subshell
– ml=0,E1, E2,… El
– E = f(n,l,m,s)
– ΔE = hν
– Si ha emissione di radiazione solo nelle
transizioni tra livelli energetici.
Proprietà dipendono soprattutto dagli
elettroni di valenza (occupano gli
orbitali più esterni).
Fermioni (Principio di esclusione di Pauli)
Spin (quarto numero quantico),s = ± 1/2.
Bande di energia
Silicio (A=14):
1s22s22p63s23p2
Germanio (A=32):
1s22s22p63s23p63d104s24p2
• Avviciniamo gli
atomi
• Guardiamo cosa
succede agli elettroni
più esterni
Bande
energetiche
• Riarrangiamento dei
livelli in bande.
• A seconda del passo
reticolare, cambia
radicalmente la
struttura.
Banda proibita
a. Isolante
b. Semi-conduttore
c. Metallo
Conduzione elettrica (metallo)
• Elettroni in un metallo
sono liberi
• Urtano continuamente
sugli atomi del reticolo
qE
a=
m
v = μΕ
Legge di Ohm
– Resistenza “viscosa” al loro
movimento
– La distanza media percorsa tra due
collisioni si chiama libero cammino
medio
– Sotto l’azione di un campo elettrico, la
velocità (di deriva) non cresce
indefinitivamente ma assume un valore
stazionario
Conduzione elettrica (metallo)
• Quindi, applicando un campo elettrico, abbiamo una
velocità di deriva (drift) vd = μEd .
• La densità di corrente è comunque data da:
– j = qnvd q=carica dell’elettrone, n densità numerica dei portatori di carica
– I = j*S S=superficie del conduttore
• vd = I/Sqn , se I = 1 A, avremo:
– S = 1mm2 = 10-6 m2 ; q=1.6 10-19 C ; n(rame)= 9 1028 atomi/m3
– vd = 1/(10-6*1.6*10-19*9 1028)=1/(1.6*9 103)= 7 10-5 m/s
• Da confrontarsi con vtermica di circa 105 m/s
1
3
2
mv = kT
2
2
T temperatura, k costante di Boltzmann, m massa dell’elettrone
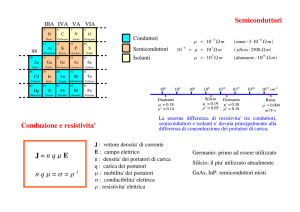
Semiconduttori
• Due tipi di portatore
– Elettroni
– Lacune
• Meccanismo di conduzione
bipolare
• Agitazione termica, libera
coppie elettrone-lacuna,
che successivamente si
ricombinano
• A regime si ha una
situzazione stazionaria con
un certo numero di
portatori liberi
Due portatori di carica
• L’elettrone mancante nei legami covalenti,
può essere schematizzato a tutti gli effetti
come una particella di carica positiva e
massa mh con mobilità μh .
+
+
+
+
t
L’elettrone che si muove a sinistra
per riempire un legame covalente,
equivale al movimento di una
carica positiva verso destra.
Sono veramente due tipi di conduzione diversa,
(schematizzabili come sopra).
Verifica sperimentale con l’effetto Hall.
Caratteristiche salienti del silicio e
del germanio
• n (concentrazione di elettroni) = p (concentrazione di lacune) = ni ( concentrazione intrinseca)
• ni2=A0T3exp-(Egap/kT) ; dipende fortemente dalla temperatura.
• j = (nμn + pμp)qE = σE
• EGAP dipende da T (10-4)
Germanio
Silicio
•
μ oltre a dipendere da T
dipende anche da E.
Numero atomico 32
14
i. Per E<103V/cm, μ è cost.
ii. Per 103<E<104, μÆE-1/2 Densità (g/cm3)
5.3
2.3
iii. Per E>104, μÆE-1
La velocità di saturazione è Atomi/cm3
4.4 1022
5.0 1022
circa 107 cm/s.
EGAP (eV) T = 300 K
0.72
1.1
ni (cm-3) T = 300 K
2.5 1013
1.5 1010
0
0
Resistività (Ωcm) 45
230000
T = 300 0K
μn (cm2/Vs) T = 300 K 3800
1300
μh (cm2/Vs) T = 300 K 1800
500
0
0
Drogaggio n
• Donori (P,As,Sb)
• Atomi con 5 elettroni negli
orbitali esterni
• Uno dei 5 elettroni, risulta poco
“legato” al suo atomo nel
reticolo
• Nella descrizione a bande, viene
introdotto un livello energetico
discreto (numero di donori comunque piccolo)
vicino alla banda di conduzione.
Drogaggio p
• Accettori (B,Ga,In)
• Atomi con 3 elettroni negli
orbitali esterni
• Uno dei 4 legami covalenti,
risulta “vuoto” e tende a
prendere l’elettrone
mancante dagli atomi vicini.
• Nella descrizione a bande,
viene introdotto un livello
energetico discreto (numero di
accettori comunque piccolo) vicino alla
banda di valenza.
Mass action law
• Quando droghiamo un semiconduttore alteriamo il
bilanciamento tra portatori. Oltre all’ovvio incremento di
elettroni (lacune) introdotti dai donori (accettori) si ha una
diminuzione dell’altra specie dovuta all’aumento del
fenomeno di ricombinazione,
• In un semiconduttore drogato chiamiamo n la concentrazione
di elettroni e p la concentrazione di lacune,
• Usiamo il suffisso i per indicare la concentrazione intrinseca,
si ha:
• np = ni2 ; Legge di azione di massa, cioè a regime il prodotto
delle concentrazioni di elettroni e lacune rimane costante
indipendentemente dal drogaggio.
Drogaggio
• Possiamo quindi cambiare le caratteristiche del
semiconduttore (es. silicio)
• La concentrazione ND di donori (tutti praticamente
ionizzati) e la concentrazione NA di accettori si
devono sommare alle concentrazioni di lacune ed
elettroni presenti nel semiconduttore. Poichè il
materiale è neutro si deve avere:
ND + p = NA + n
• In un semiconduttore di tipo n (NA = 0) p è molto
piccola e quindi Æ n ≈ ND
• Inoltre np = ni2 Æ p ≈ ni2/ND
Qualche numero (silicio)
• Aggiungiamo donori; una parte in 108 atomi di
silicio:
• ND = 5.0 1022 /108 = 5.0 1014
• n ≈ 5 1014
• p ≈ ni2/ND=2.25 1020/5 1014 = 4.5 105
• La resistività diventa:
– σ = nqμn = 5 1014 * 1.6 10-19 * 1300 = 1.04 10-1 (Ωcm)-1
– ρ = 1/σ = 10 Ωcm
Sono davvero due tipi di portatori !
• Effetto HALL
• F = qvB diretta lungo -Y
Effetto Hall
• Se il silicio è di tipo n, la corrente sarà data da
elettroni liberi (carica negativa) che si muovono
da destra a sinistra. Se di tipo p da lacune (carica
positiva) che si muovono da sinistra a destra. In
ogni caso migrano sulla faccia 1.
– Vhall = V21 > 0 se di tipo n
– Vhall = V21 < 0 se di tipo p
• Se la conduzione nel materiale di tipo p fosse
dovuta ad elettroni legati che si muovono da destra
a sinistra Vhall sarebbe uguale nei due casi. La
lacuna si comporta classicamente come un
portatore libero di carica positiva.
Effetto Hall (tipo n)
• E = VHall/d , le cariche accumulate sulle superfici
generano un campo elettrico E tale da contrastare un
ulteriore spostamento di cariche dovuto alla forza di
Lorentz.
– VHall = Ed = Bvd ; j = nqv = I/wd
– VHall = BI/nqw da cui si ricava la densità di portatori nq.
• RHall = 1/nq , coefficiente di Hall.
• Se viene misurata anche la conducibilità σ = nqμ si
ricava anche il valore della mobilità μ.
• Vale ovviamente anche per materiale di tipo p; si ricava la
mobilità delle lacune.
Resistività di un semiconduttore
• Forte dipendenza dalla temperatura (8% per
grado nel silicio).
– Al contrario dei metalli la resistività scende all’aumentare
della temperatura. (generazione di coppie, libero cammino medio).
– I semiconduttori vengono quindi usati come termistori
(Mn2O3, ecc.)
• Sensibilità alla luce.
– La radiazione incidente, se sufficientemente energetica può
creare coppie elettrone-lacune.
– In generale le eccitazioni sono di tipo intrinseco. Cioè è
necessario che la radiazione sia di energia comparabile al
bandgap del materiale (silicio 1.1 eV).
Generazione e ricombinazione dei
• Creazione continua di coppie
portatori (1 passo verso l’eqz. di continuità)
e-h per agitazione termica
o
•
•
•Aumentiamo la produzione di coppie e-h
con uno stimolo luminoso
•Al tempo t=0 interrompiamo lo stimolo
Ricombinazione tra coppie
e-h è proporzionale alla loro
concentrazione
Supponiamo di avere un
materiale di tipo n (portatori
maggioritari gli elettroni)
Generazione e ricombinazione dei
portatori (1 passo verso l’eqz. di continuità)
o
• Consideriamo solo i portatori minoritari, le lacune, infatti:
• L’incremento percentuale dei maggioritari dovuta all’illuminazione è
trascurabile rispetto a quello dei minoritari
• Cessato lo stimolo luminoso, la popolazione dei minoritari tornerà
al livello iniziale p0 .
• La ricombinazione, come abbiamo detto, sarà proporzionale alla
concentrazione di lacune. Chiamiamo 1/τp la costante di
proporzionalità in questione. 1/τp non dipende dalla stessa
concentrazione.
• Abbiamo quindi:
– p/τp = al decremento della concentrazione di portatori minoritari al secondo
per via della ricombinazione,
– g = all’incremento della concentrazione di portatori minoritari al secondo per
via dell’agitazione termica
Generazione e ricombinazione dei
portatori (1 passo verso l’eqz. di continuità)
o
• La variazione temporale di p sarà quindi:
• dp = g − p , conservazione della carica.
dt
τp
• All’equilibrio p = p0 , dp/dt = 0. Quindi:
–
g = p0/τp . L’equazione diventa:
dp p 0 - p
=
τp
dt
– All’istante t=0, p(0) = p’(0) + p0 , dove p’(0) sono i
portatori in eccesso dovuti all’illuminazione del
campione.
Generazione e ricombinazione dei
portatori (1 passo verso l’eqz. di continuità)
o
• La soluzione dell’equazione che rispetti le condizioni al
− t
contorno:
p(t) = p' (0)e
τp
+ p0
• La decrescita dell’eccesso di portatori ha un andamento
esponenziale con il tempo.
• τp assume il significato di vita media dei portatori.
• La ricombinazione difficilmente avviene per via diretta. La
conservazione della quantità di moto richiede pe= -ph , serve
quindi un terzo corpo.
• Impurezze e difetti nel reticolo sono degli efficaci terzi
incomodi, e di conseguenza accorciano la vita media dei
portatori.
• τp in generale varia da qualche ns a centinaia di μs.
Correnti in un semiconduttore
(2o passo verso l’eqz. di continuità)
• Corrente di drift: ad es.
– Jp = pqμpE
• Ma anche corrente di diffusione, (non esiste nei
metalli), legata alla presenza di gradienti di
concentrazione dei portatori.
– Jp = -qDp dp/dx , con il segno meno perchè la corrente va
dove la concentrazione di portatori diminuisce.
– Dp è il coefficiente di diffusione, (m2/s)
• Esattamente uguale a quello che succede con i gas, non
è un fenomeno legato alla repulsione elettrica tra le
cariche. E’ un fenomeno statistico.
Correnti in un semiconduttore
(2o passo verso l’eqz. di continuità)
S
Jp
densità
maggiore
densità
minore
• Ad un qualsiasi istante più lacune
passano da destra a sinistra che
viceversa
• L’intensità di questa corrente è
inversamente proporzionale al
gradiente della concentrazione.
• Si possono avere in contemporanea
sia un gradiente di potenziale che di
concentrazione. La corrente diventa:
– Jp = q(pμpE - Dp dp/dx )
– Jn = q(nμnE + Dn dn/dx )
Relazione di Einstein
• Mobilità e diffusione sono fenomeni
termodinamici legati tra di loro dalla
relazione:
Dn Dp
kT
=
= VT ; VT =
μn μp
q
• VT è il Volt equivalente della temperatura.
Equazione di continuità
(ovvero la carica si conserva)
Ip
A = superficie laterale
Ip = corrente in ingresso
p
A Ip + dIp
La variazione del numero di lacune nel volumetto
Adx per unità di tempo, è data dal termine di
generazione di coppie e-h per agitazione termica,
dal termine dovuto alla ricombinazione e dalla
differenza tra la corrente entrante ed uscente dal
volume in questione.
• dIp è uguale alla diminuzione di
carica per unità di tempo
all’interno del volumetto A*dx .
1 dI p
1 dJ p
=
q Adx q dx
rappresenta la diminuzione
della densità di lacune per
unità di tempo
• La variazione di carica all’interno
del volumetto Adx, deve tenere
conto anche di queste correnti.
• Si ha quindi:
∂p p 0 - p 1 ∂J p
=
−
∂t
τp
q ∂x
Low level
injection
• Esponiamo un lato
del semiconduttore
alla luce (in maniera
stazionaria)
• Di conseguenza si
creano all’interno del
volume in prossimità
di quel lato delle
coppie e-h.
Low Level Injection
• p = p’(0) + p0 << n
!! L.L.I.
• Possiamo trascurare la corrente di deriva (drift)
delle lacune rispetto a quella di diffusione.
– la corrente di deriva è proporzionale alla densità di portatori
– verifica a posteriori
• Quindi la corrente Ip è solamente di diffusione (ma
non la In !!!)
– Jp = -qDp dp/dx
– Jn = q(nμnE + Dn dn/dx )
Low Level Injection
• Stazionarietà:
∂p
=0 Æ
∂t
p 0 - p 1 ∂J p
=
τp
q ∂x
p0 - p
∂ p
= −D p 2
Æ
τp
∂x
2
• Jp solo di diffusione
• Lp = √Dpτp è una lunghezza.
• p’ = p - p0 = eccesso di portatori
∂ p' p'
=
2
2
∂x
Lp
2
L.L.I. soluzione
p' (x) = p' (0)e
x
−
Lp
• L’eccesso di portatori decresce esponenzialmente verso il
valore stazionario p0 .
• Lp non è solo la distanza alla quale la concentrazione dei
portatori decresce di 1/e, ma è anche la distanza media
percorsa dalla lacuna prima di ricombinarsi.
Distanza media
dp'
1
=−
p' (0)e
dx
Lp
dx
| dp' | =
p' (0)e
Lp
−
x
Lp
x
−
Lp
•
dp’ rappresenta la frazione di lacune iniettate che
si sono ricombinate tra x e x+dx
∫
∞
Quindi 0 x | dp | rappresenta la somma di
tutte le distanze percorse dalle lacune iniettate
La distanza media percorsa dai portatori è quindi:
•
•
1 ∞
1
x=
x | dp |=
∫
p' (0) 0
Lp
_
∫
∞
0
xe
-
x
Lp
dx
1 2
x=
Lp = Lp
Lp
_
Correnti di diffusione
• Jp = -qDp dp/dx Æ
Jp = q
Dp
Lp
I p = Aq
p' (0)e
Dp
Lp
−
x
Lp
(p(0) - p 0 ) e
−
x
Lp
• Con l’illuminazione creiamo un egual numero di
elettroni e lacune
– Abbiamo quindi:
• n’ = p’ Æ n – n0 = p – p0
• n0 e p0 sono concentrazioni stazionarie che NON dipendono da x
• Di conseguenza:
dp dn
=
dx dx
Correnti di diffusione
• Jn = qDn dn/dx = qDn dp/dx
Dn
≅ 3 (Si)
Dp
• dp/dx = - Jp / qDp
• Quindi:
Dn
Jn = −
Jp
Dp
Dn
In = −
Ip
Dp
• Si hanno due correnti di diffusione di magnitudo
comparabile.
Corrente totale
• Per ovvi motivi, la corrente totale nella sbarretta di
semiconduttore deve essere nulla (circuito aperto)
• Quindi ci deve essere una corrente di deriva che
annulla la corrente di diffusione.
drift
diff
In + In + I
Perchè esista una corrente di deriva
deve esserci un campo elettrico
nella sbarra. Questo viene creato
proprio dall’iniezione di portatori.
I
drift
n
= Aqnμ n E
I drift
n
diff
p
=0
⎛
⎞
D
n
⎜
= I diff
− 1⎟
p ⎜
⎟
D
⎝ p ⎠
⎛ Dn ⎞
⎜
E=
− 1⎟
Aqnμ n ⎜⎝ D p ⎟⎠
I
diff
p
Corrente totale
• Possiamo verificare ora la correttezza dell’ipotesi fatta in
precedenza sulla trascurabilità della corrente di deriva delle lacune
I
I
drift
p
drift
p
= Aqpμ p E
=
Aqpμ p
Aqnμ n
⎛ Dn ⎞
⎜
E=
− 1⎟
Aqnμ n ⎜⎝ D p ⎟⎠
I
p << n
I
diff
p
diff
p
⎛ Dn ⎞
diff
⎜
⎟
− 1 << I p
⎜D
⎟
⎝ p ⎠
Drogaggio non uniforme (2)
• Abbiamo visto che si genera
una corrente di diffusione.
• Siamo in condizioni stazionarie
senza stimoli esterni.(Solo agitazione termica).
S
P1
P2
– Jp = q(pμpE - Dpdp/dx )
Jp
densità
maggiore
x1
• Se la sbarretta è isolata: Jp = 0
– pμpE - Dpdp/dx = 0
– Rel. di Einstein Dp/μp = VT
– E = - dV/dx
V dp
E= T
p dx
densità
minore
x2
x
dp
dV = −VT
p
Drogaggio non uniforme (2)
• Integrando tra i punti x1 e x2 (concentrazioni p1 e p2) :
⎛ p2 ⎞
V21 = V2 − V1 = − VT ln⎜⎜ ⎟⎟
⎝ p1 ⎠
• V21 dipende solo dalle concentrazioni in x1 e x2 (scelti
arbitrariamente).
• Questa equazione può essere rigirata in modo da
ottenere la relazione di Boltzmann proveniente dalla
teoria cinetica dei gas.
p1 = p 2 e
V21
VT
Cosa non uniforme più di una
giunzione p-n ? Magari a gradino!
p
n
NA
ND
• pp0 ≈ NA
• pn0 ≈ ni2/ND
⎛ p n0 ⎞
⎟
V0 = −VT ln⎜
⎜p ⎟
⎝ p0 ⎠
p n0 = p p0 e
−
V0
VT
Usiamo le concentrazioni di lacune
nel materiale p (maggioritari) ed n (minoritari).
⎛ NA ND ⎞
⎟⎟
V0 = VT ln⎜⎜
2
⎝ ni ⎠
I due blocchi messi a contatto sviluppano una
differenza di potenziale interna pari a V0.
Mass action law (2)
p1 = p 2 e
• Se calcoliamo le differenze di potenziale in usando la
diffusione degli elettroni, Jn = 0, otteniamo:
n1 = n 2 e
−
• Il prodotto delle due concentrazioni:
n1p1 = n 2 p 2 e
V21
VT
e
−
V21
VT
= n 2p2
– è costante e non dipende da x (e quindi dal drogaggio stesso)!
Deve valere quindi, anche per un semiconduttore intrinseco
dove n = p = ni !!
• Abbiamo quindi la legge di azione di massa:
np = ni2
V21
VT
V21
VT
Giunzione p-n
E=−
x ρ
dV
= ∫ dx
x0 ε
dx
d 2V
ρ
=
−
dx 2
ε
• Le lacune che si
diffondono nella zona N
si ricombinano con gli
elettroni presenti,
lasciando ionizzati gli
ioni donori. Si viene a
creare quindi una zona
“fissa” di carica
positiva. Lo stesso
accade per gli elettroni
che diffondono nella
zona P.
• Queste cariche nude,
danno origine ad un
campo elettrico E che
ostacola l’ulteriore
diffusione di portatori.
Giunzione p-n
⎛ NA ND ⎞
⎟⎟
V0 = VT ln⎜⎜
2
⎝ ni ⎠
• Si ha quindi la creazione di una barriera di potenziale
che ostacola il movimento dei portatori maggioritari da
una parte all’altra della giunzione.
• Questo potenziale, come già visto, dipende dai livelli di
drogaggio del materiale. Tipicamente è dell’ordine dei
decimi di Volt.
Giunzione p-n
•
•
•
Quando applichiamo una tensione V ai capi della giunzione questa si somma al
potenziale di contatto. A seconda della polarità potrà o abbassare o innalzare la
barriera presente alla giunzione favorendo o meno l’iniezione di portatori da una
zona all’altra del materiale.
Quindi in polarizzazione “diretta”, avremo un’iniezione di lacune(elettroni) dalla
zona P(N) alla zona N(P), un’iniezione cioè di portatori minoritari nella zona N(P)
che noi assumeremo rispetti le condizioni di Low Level Injection.
Di conseguenza assumeremo che le correnti iniettate a x=0 (zona di contatto tra i
due materiali) siano puramente di diffusione.
I
Corrente totale del diodo, I
I
P
Giunzione asimmetrica
p>>n
Ip n(0)
Vg
+ N
Ip n(0)+ Inp (0)
Ip n(x) c orrente d i diffusione
delle lac une
Inp (0)
Ad x=0, è presente solo la diffusione
dei portatori iniettati. Allontanandoci dalla giunzione
la corrente di diffusione decade esponenzialmente.
0
Inp (x)c orrente d i diffusione
deg li elettroni
X
•
Giunzione p-n
•
Giunzione asimmetrica
p>>n
•
Ad x=0, è presente solo la
diffusione dei portatori
iniettati. Allontanandoci
dalla giunzione la corrente
di diffusione decade
esponenzialmente.
Ma la corrente totale deve
rimanere costante. Si ha
quindi la comparsa di una
corrente di deriva, dovuta al
campo elettrico presente nel
semiconduttore.
Ad x=0 abbiamo quindi
(lacune):
dp
J p = −qD p
dx
p' (x) = p' (0)e
I pn = Aq
Dp
Lp
(p(0) - p 0 ) e
−
x
Lp
⇒
AqD p
Lp
−
x
Lp
(p n (0) - p n0 )
Per gli elettroni nel materiale p vale la
stessa espressione scambiando n con p
Giunzione p-n
• Per procedere dobbiamo trovare la dipendenza di pn(0) dalla
tensione V applicata ai capi della giunzione.
p1 = p 2 e
V21
VT
p n (0) = p p0 e
V − V0
VT
•Abbiamo visto precedentemente come
variazioni nella concentrazione dei
portatori (drogaggio non-uniforme)
fossero legate tra loro dalla relazione di
Boltzmann. Si può assumere
ragionevolmente che la dipendenza di
pn(0) dalla tensione applicata sia simile.
•Si assume, quindi, che le lacune iniettate
appena a ridosso della zona N dipendano
dalla concentrazione all’equilibrio
termico pp0 e dalla differenza tra V
applicata ed il potenziale di contatto V0 .
Legge della giunzione
I pn =
AqD p
Lp
p n (0) = p p0 e
(p n (0) - p n0 )
Corrente di diffusione dovuta alle lacune
iniettate dal materiale p nel materiale n.
• pp0 la concentrazione di lacune
all’equilibrio termico nel materiale
p è esprimibile in termini di pn0
ossia della concentrazione di
lacune all’equilibrio termico nel
materiale n .
V − V0
VT
V21 = V0 = VT ln
p n (0) = p n0 e
V
VT
p p0
p n0
p p0 = p n0 e
V0
VT
Questa relazione si chiama legge della
giunzione.
La legge del diodo
V
⎛
AqD p p n0 VT ⎞
⎜ e - 1⎟
Ip =
⎜
⎟
Lp
⎝
⎠
• Sostituendo abbiamo
per le lacune:
• Per gli elettroni vale
un’espressione simile:
• La somma delle due è
la corrente totale che
scorre nel diodo:
• Con: I 0 =
AqD n n p0
Ln
+
V
⎛
AqD n n p0 VT ⎞
⎜ e - 1⎟
In =
⎜
⎟
Ln
⎝
⎠
⎛ VV ⎞
I = I 0 ⎜ e T - 1⎟
⎜
⎟
⎝
⎠
AqD p p n0
Lp
Alcuni numeri
• A temperatura ambiente (300 K) I0 è
dell’ordine dei nA per il silicio e dei μA per
il Germanio.
• I0 dipende fortemente dalla temperatura
(attraverso le concentrazioni di portatori n0
e p0, attraverso Lp e Ln, e attraverso i
coefficienti di diffusione Dn e Dp). I0 nel
silicio varia di circa l’8% per ogni grado.
Capacità (transizione)
di un diodo
• Diodo inversamente
polarizzato!
• Aumentando la contropolarizzazione si allarga la
zona di svuotamento e si
incrementano le cariche
“nude” dei donori e degli
accettori.
– In pratica abbiamo un
comportamento capacitivo
• Definiamo la capacità di
transizione come rapporto
incrementale:
dQ
CT =
dV
Capacità di transizione
• Giunzione asimmetrica:
– NA >> ND
• Il diodo rimane neutro, la carica netta totale deve
essere zero, quindi:
– WpNA = WnND Æ Wp << Wn
– Wp è lo spessore della zona svuotata nel materiale p,
Wn nel materiale n.
– Trascuriamo anche la piccola caduta di potenziale nella
zona p.
Capacità di transizione
2
• Eqz. di Poisson:
d V
qN D
=−
2
dx
ε
• W≈Wn ; E(W) = 0 condizione al contorno
dV qN D
• Il campo elettrico: E = −
(x − W )
=
dx
ε
• Il potenziale è definito a meno di una
costante, imponiamo che V(x=0) = 0:
(
qN D 2
V=−
x - 2Wx
2ε
)
Capacità di transizione
• A x=W ÆV = Vj diventa uguale al voltaggio applicato alla
zona di transizione.
– Cioè Vj = V0 -Vgen
qN D 2
Vj =
W
2ε
2ε
W=
Vj
qN D
• Abbiamo quindi:
• e ancora:
• La carica totale è : Q=qNDWA
• Si ricava quindi CT:
dQ dQ dW
=
=
CT =
dV dW dV
ε
εA
=
qN D A
WqN D
W
Capacità di transizione
• Uguale a quella di un condensatore a facce
piane parallele.
Rettificatore
• Il diodo è un componente circuitale che
permette il passaggio della corrente in una
sola direzione.
• Realizzazioni pratiche di vario tipo:
– Diodi a semiconduttore (silicio,germanio)
– Diodi a valvola
Tipo di diodi
• Valvole
• Semiconduttori
Giunzione PN
• Silicio, due tipi di portatore
di carica:
– elettroni (Silicio tipo N)
– lacune (Silicio tipo P)
• Regione “svuotata” estremamente sottile
• Creazione di una barriera di potenziale
– Impedisce l’ulteriore movimento delle cariche
– Viene influenzata da una polarizzazione
esterna
Diodo a giunzione
• Polarizzazione diretta (figura)
– Generatore “abbassa” la barriera e favorisce il
flusso dei portatori di carica “maggioritari”
Circuito con un diodo
• Caratteristica V-A (Volt-Ampere) del diodo
Caratteristica V-A del diodo
• I = I0 (eV/ηV -1)
t
–
–
–
–
I0 = Corrente di saturazione inversa
V = Tensione di polarizzazione esterna
Vt = Volt equivalente della temperatura
η = Coefficiente di correzione
silicio/germanio
Parametri
•
•
•
I0 ~ μA (Germanio) ~nA (Silicio) a
temperatura ambiente
Vt = 0,026 V
η = 1 (Germanio) , 2 (Silicio)
•Resistenza statica (V/I) varia enormemente con V e I
•Piú importante la resistenza dinamica rD = dV/dI ~ 1Ω (Vbias= 0.2 V, Ge)
1 dI
e
=
= I0
ηVt
rD dV
V
ηVt
I + I0
=
ηVt
Funzione di trasferimento
•
•
•
•
Curva statica
Curva dinamica
Retta di carico
Piece wise approx.
Diodo in laboratorio
Misura caratteristica I-V di un diodo con un
multimetro (almeno 5 punti) e con il caratteristigrafo.
• DIODO:
– Eseguire 5 misure per 5 diversi valori di Vi con
Rload fissata a 1000 Ohm. Con 0,5V < Vi < 5V.
– Mettere in grafico la curva dinamica del diodo.
– Determinare Vγ, e Rf (1mA < I < 3mA).
Diodo in laboratorio
• Tracciare la curva del diodo con il
caratteristigrafo, sia in polarizzazione
diretta che inversa. Durante la scansione di
quest’ultima scaldate il diodo con la punta
di un saldatore acceso a 100 gradi.
– Vi – V –iRload = 0 -- > V=Vi – iRload (Retta di
carico).
• le curve sono limitate da Rload o da Pmax?
Il caratteristigrafo
Non solo diodi .....
Caratteristigrafo
• BREVE DESCRIZIONE DEL TRACCIATURE DI CURVE
CARATTERISTICHE TEKTRONIX 571
• Dopo avere pigiato il tasto MENU , selezionare sullo schermo , alla
riga Function , l'opzione <Acquisition> e alla riga Type [NPN PNP NFET P-FET DIODE S.C.R. ] il dispositivo utilizzato .
• La selezione delle righe e delle relative opzioni sullo schermo menu si
ottiene con i quattro tasti contrassegnati da altrettante frecce indicanti i
movimenti verso l'alto(UP) , verso il basso(DOWN) , verso sinistra
(LEFT) e verso destra (RIGHT) . La riga selezionata e' marcata da un
rettangolo luminoso alla sua sinistra , l'opzione selezionata appare
invertita .
Menu diodo
Nel caso di Type Diode occorre selezionare :
•
il fondo scala delle tensioni anodo catodo
–
•
il fondo scala della corrente
–
•
I max [0.05 0.1 0.2 0.5 1 5 10 ....2000]mA
la resistenza di carico
–
•
V max [0.5 1 2 5 10 20 50 100] Volt
Rload [ Ik 100 10 0.25] Ohm
la potenza massima dissipabile sul dispositivo
sotto test
–
Pmax [0.1 0.5 2 1 100] Watt
Acquisizione
• Definito il menu , pigiare il tasto START :
lo schermo viene aggiornato e le
caratteristiche sono tracciate .
• Per interrompere l'acquisizione , se
necessario , pigiare il tasto STOP .
• A tracciatura ultimata , pigiare il tasto
CURSOR e leggere i valori V & I al lato
dello schermo.