I.I.S. “Via Domizia Lucilla”
Via Cesare Lombroso, 118 Roma
Programmazione didattica Dipartimento di Matematica
anno scolastico 2016/2017
QUADRO DEGLI OBIETTIVI DI COMPETENZA- ASSE MATEMATICO
Competenze disciplinari del I
Biennio
Obiettivi generali di competenza della
disciplina definiti all’interno del
Dipartimento
1.
2.
3.
4.
Utilizzare le tecniche e le procedure del calcolo
aritmetico ed algebrico, rappresentandole anche
sotto forma grafica.
Confrontare ed analizzare figure geometriche,
individuando invarianti e relazioni.
Individuare le strategie appropriate per la soluzione
di problemi.
Analizzare dati e interpretarli sviluppando
deduzioni e ragionamenti sugli stessi anche con
l’ausilio di rappresentazioni grafiche, usando
consapevolmente gli strumenti di calcolo ed
eventualmente utilizzando applicazioni specifiche
di tipo informatico.
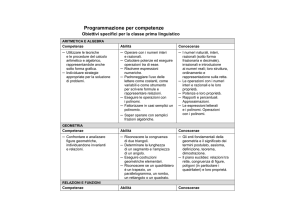
ARTICOLAZIONE DELLE COMPETENZE IN ABILITA’ E CONOSCENZE del I biennio
COMPETENZE
ABILITA’
1. Utilizzare le tecniche e le Aritmetica e algebra
procedure del calcolo aritmetico ed Utilizzare le procedure del calcolo
algebrico, rappresentandole anche aritmetico (a mente, per iscritto, a
macchina) per calcolare espressioni
sotto forma grafica.
aritmetiche e risolvere problemi;
operare con i numeri interi e
razionali e valutare l’ordine di
grandezza dei risultati. Calcolare
semplici espressioni con potenze e
radicali. Utilizzare correttamente il
concetto di
approssimazione.
Padroneggiare l’uso della lettera
come mero simbolo e come
variabile; eseguire le operazioni con i
polinomi; fattorizzare un polinomio.
CONOSCENZE
Aritmetica e algebra
I numeri: naturali, interi, razionali,
sotto forma frazionaria e decimale,
irrazionali e, in forma intuitiva,
reali; ordinamento e loro
rappresentazione su una retta. Le
operazioni con i numeri interi e
razionali e le loro proprietà.
Potenze e radici. Rapporti e
percentuali. Approssimazioni.
Le espressioni letterali e i polinomi.
Operazioni con i polinomi.
2. Confrontare ed analizzare figure Geometria
Geometria
Gli enti fondamentali della
geometria e il significato dei termini
postulato, assioma, definizione,
teorema, dimostrazione. Nozioni
fondamentali di geometria del
piano. Le principali figure del
piano.
Il piano euclideo: relazioni tra rette,
Poligoni e loro proprietà.
Circonferenza e cerchio. Perimetro
e area dei poligoni. Teorema di
Pitagora.
Individuare le strategie Relazioni e funzioni
appropriate per la soluzione di Risolvere equazioni di primo e
secondo grado;
problemi.
risolvere sistemi di equazioni.
Risolvere problemi che implicano
l’uso di equazioni e di sistemi di
equazioni anche per via grafica,
collegati con altre discipline e
situazioni di vita ordinaria, come
primo passo verso la
modellizzazione matematica.
Relazioni e funzioni
Linguaggio degli insiemi. Funzioni
di tipo lineare.
Equazioni di primo e secondo
grado. Sistemi di equazioni.
Il metodo delle coordinate: il piano
cartesiano. Rappresentazione
grafica di funzioni lineari.
g e o m e t r i c h e , i n d i v i d u a n d o Conoscere e usare misure di
grandezze geometriche: perimetro,
invarianti e relazioni.
area delle principali figure
geometriche del piano.
3.
4. Analizzare dati e interpretarli
sviluppando deduzioni e
ragionamenti sugli stessi anche con
l’ausilio di rappresentazioni
grafiche, usando consapevolmente
gli strumenti di calcolo
Utilizzare proporzioni e percentuali
anche in altri ambiti disciplinari
Concetto di proporzione, proprietà
delle proporzioni uso delle
proporzioni per calcolare
percentuali, interesse, sconto
Competenze disciplinari del Secondo
Biennio
Obiettivi generali di competenza della
disciplina definiti all’interno dei Dipartimenti
1. Utilizzare le tecniche e le procedure del calcolo
aritmetico ed algebrico, rappresentandole anche
sotto forma grafica.
2. Confrontare ed analizzare figure geometriche,
individuando invarianti e relazioni.
3. Rappresentare e studiare le proprietà di
semplici luoghi geometrici, in particolare della
retta, parabola, utilizzando queste ultime anche
come modelli geometrici in contesti reali
4. Analizzare dati e interpretarli sviluppando
deduzioni e ragionamenti sugli stessi anche con
l’ausilio di rappresentazioni grafiche, usando
consapevolmente gli strumenti di calcolo.
5. Utilizzare il linguaggio e i metodi propri della
matematica per organizzare e valutare
adeguatamente informazioni qualitative e
quantitative.
ARTICOLAZIONE DELLE COMPETENZE IN ABILITA’ E CONOSCENZE
COMPETENZE
ABILITA’
CONOSCENZE
1. Utilizzare le tecniche e le Aritmetica e algebra
Aritmetica e algebra
I numeri: naturali, interi,
razionali,irrazionali,
e in forma intuitiva i reali; come si
risolvono semplici equazioni
irrazionali, logaritmiche ed
esponenziali. Disequazioni, intere e
fratte, sistemi di disequazioni.
2. Confrontare ed analizzare figure Geometria
Geometria analitica
Piano cartesiano, coordinate punto
medio e distanza fra due punti
calcolo del perimetro e dell’area area
di figure piane
procedure del calcolo aritmetico ed Utilizzare le procedure del calcolo
algebrico, rappresentandole anche aritmetico (a mente, per iscritto, a
macchina) per calcolare espressioni
sotto forma grafica.
aritmetiche e risolvere problemi;
operare con i numeri interi e razionali
e irrazionali, saper risolvere equazioni
di primo e secondo grado e sistemi
lineari.
g e o m e t r i c h e , i n d i v i d u a n d o Conoscere e usare misure di
grandezze geometriche: perimetro,
invarianti e relazioni.
area delle principali figure
geometriche del piano.
3.
Rappresentare e studiare le
proprietà di semplici luoghi
geometrici in particolare della retta,
della parabola utilizzandole anche
come modelli geometrici in contesti
reali
Geometria analitica
Rappresentare sul piano cartesiano le
rette,e le parabole.
Risolvere problemi che implicano
l’uso di funzioni, di equazioni e di
sistemi di equazioni anche per via
grafica, collegati con altre discipline e
situazioni di vita ordinaria, come
primo passo verso la modellizzazione
matematica. Individuare la strategia
più appropriata per la risoluzione di
problemi
Geometria analitica
Funzioni di tipo lineare.
Interpretazione grafica dei sistemi di
equazioni.
Il metodo delle coordinate: il piano
cartesiano. Rappresentazione
grafica di funzioni lineari.
Rappresentazione grafica di parabole
e problemi relativi
4. Utilizzare il linguaggio e i
metodi propri della matematica per
organizzare e valutare
adeguatamente informazioni
qualitative e quantitative.
Saper esporre i concetti, dedurre
proprietà ed eseguire collegamenti
Competenze disciplinari del quinto anno
Obiettivi generali di competenza della
disciplina definiti all’interno dei Dipartimenti
Linguaggio specifico della disciplina
1. Utilizzare le tecniche e le procedure del calcolo
aritmetico ed algebrico, rappresentandole anche
sotto forma grafica.
2. Confrontare ed analizzare figure geometriche,
individuando invarianti e relazioni.
3. Analizzare dati e interpretarli sviluppando
deduzioni e ragionamenti sugli stessi anche con
l’ausilio di rappresentazioni grafiche, usando
consapevolmente gli strumenti di calcolo.
4. Utilizzare il linguaggio e i metodi propri della
matematica per organizzare e valutare
adeguatamente informazioni qualitative e
quantitative.
5. Individuare le caratteristiche generali di una
funzione.
ARTICOLAZIONE DELLE COMPETENZE IN ABILITA’ E CONOSCENZE
COMPETENZE
ABILITA’
CONOSCENZE
1. Utilizzare le tecniche e le Saper risolvere disequazioni e sistemi Disequazioni intere di I e II grado
procedure del calcolo algebrico, di disequazioni.
rappresentandole anche sotto forma
grafica
Disequazioni fratte
2. Collegare insiemi attraverso Saper distinguere relazioni da
relazioni o funzioni
funzioni
Saper riconoscere funzioni suriettive,
iniettive e biiettive.
Concetto di relazione e di funzione
Proprietà delle funzioni
3. Utilizzare i primi strumenti Analisi matematica
Analisi matematica
Intervalli di una retta
Definizione e classificazione di
funzioni.
Dominio di una funzione
dell’analisi per affrontare situazioni Sapere costruire e riconoscere i vari
p r o b l e m a t i c h e , e l a b o r a n d o intervalli di una retta.
Saper riconoscere e classificare le
opportune soluzioni
funzioni.
Saper individuare il dominio di una
funzione
4. Intuire l’andamento di una
funzione mediante l’utilizzo del
calcolo infinitesimale.
Calcolo infinitesimale
Comprendere il concetto di limite
Saper operare con i limiti di semplici
funzioni
Saper dedurre se il grafico di una
funzione presenta asintoti verticali e
orizzontali
Calcolo infinitesimale
Concetto di limite
Limiti di forma determinate ed
indeterminate.
Operazioni sui limiti
Concetto di asintoto orizzontale e
verticale
5.Utilizzare gli strumenti del
calcolo differenziale e interpretare
dal punto di vista geometrico il
concetto di derivata.
6.Saper leggere un grafico di
funzione
Continuità e derivabilità
Riconoscere i punti di discontinuità
Saper calcolare le derivate di semplici
funzioni
Saper individuare i punti di massimo
e di minimo assoluti e relativi.
Continuità e derivabilità
Concetto di continuità di una
funzione
Punti di discontinuità
Concetto di derivabilità
Significato geometrico di derivata
Calcolo di derivate di funzioni
razionali
Calcolo dei punti di massimo e
minimo di semplici funzioni
Saper interpretare un qualsiasi grafico Il grafico di funzione.
di funzione tratto anche da esempi
reali, in particolare individuando gli
intervalli di monotonìa e i punti di
massimo e minimo