TIPI DI TRIANGOLI

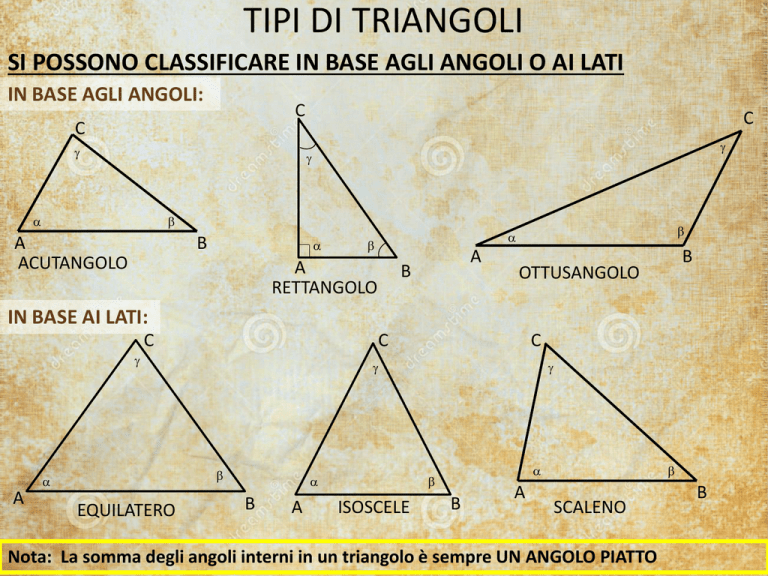
TIPI DI TRIANGOLI
SI POSSONO CLASSIFICARE IN BASE AGLI ANGOLI O AI LATI
IN BASE AGLI ANGOLI:
C
C
g
C
g
g
a
b
A
ACUTANGOLO
B
a
b
a
b
A
RETTANGOLO
A
B
B
OTTUSANGOLO
IN BASE AI LATI:
C
C
g
A
g
b
a
EQUILATERO
C
a
B
A
g
a
b
ISOSCELE
B
A
b
SCALENO
Nota: La somma degli angoli interni in un triangolo è sempre UN ANGOLO PIATTO
B
AREA DI UN TRIANGOLO
Se conosciamo due lati e l’angolo fra essi compreso l’area si può calcolare nel seguente modo:
S ABC
1
  AB  BC  senb
2
oppure
C
S ABC
g
1
  AB  AC  sena
2
oppure
a
A
b
B
S ABC
1
  BC  AC  seng
2
RISOLUZIONE DEI TRIANGOLI QUALSIASI
C
g
a
b
A
B
SI POSSONO APPLICARE DUE TEOREMI:
TEOREMA DEI SENI
quando conosco:
- DUE LATI E UN ANGOLO OPPOSTO
(es. AB, BC, g)
- DUE ANGOLI E 1 LATO
(es. a, b, AB)
TEOREMA DI CARNOT (COSENO)
quando conosco:
- DUE LATI E UN ANGOLO COMPRESO
(es. AB, BC, b)
- TRE LATI
(AB, BC, AC)
Nota:
Non si può risolvere un triangolo conoscendo solo i 3 angoli!
TEOREMA DEI SENI
In un triangolo qualsiasi il rapporto tra una lato ed il seno dell’angolo opposto è costante e
uguale al diametro della circonferenza circoscritta
AB
BC
AC


 2r
seng sena senb
C
g
La proporzione va usata scrivendo due termini per
volta e non deve comparire più di una incognita.
Esempio:
Se conosco AB, BC e a si scriverà:
O
b
a
A
B
r
AB
BC
1  AB  sena 

 g  sen 

seng sena
 BC 
Se conosco BC, a, b si scriverà:
BC
AC
BC  senb

 AC 
sena senb
sena
NOTA: questo teorema ha un inconveniente quando si ricavano gli angoli (approfondire)
TEOREMA DI CARNOT (COSENO)
Se conosciamo due lati e l’angolo compreso si
può ricavare il terzo lato. Ad esempio con AB,
BC e b si ha:
C
AC  AB 2  BC 2  2  AB  BC  cos b
g
a
A
b
B
Se conosciamo tre lati si possono ricavare gli
angoli:
a  cos
1
b = …..
g = …..
AB
 AC 2  BC 2
2  AB  AC 
2

ESERCIZIO N.3
B
Dati
AC = 96,61 m
BCA = g = 109c,4719
CAB = a = 61c,1005
Svolgimento
Si può subito trovare il terzo angolo:
b = 200c – a – g = 29c,4276
b
g
C
a
96,61
A
BC
AC
AC  sena

 BC 
 177,43 m
sena senb
senb
Il terzo lato si può trovare sempre con il teorema dei seni oppure di Carnot:
AB  AC 2  BC 2  2  AC  BC  cos g  214,24 m
S ABC
1
  AB  AC  sena  8476,30 m 2
2
ESERCIZIO N.1
55
0,
87
A
A'
g
7
550,8
B
596,80
Triangolo ABC, teorema dei seni
Dati
AB = 550,87 m
BC = 596,80 m
g = BCA = 62°45'16"
Svolgimento
Si mette in DEG e si trasforma l’angolo:
C g  62 
45 16

 62,7544
60 3600
BC
AB
 BC  seng 

 a  sen 1 
  74,4035
sena seng
AB 

b = 180° - a – g = 42°,8421
1
AC
AB
AB  senb
S

 AB  AC  sena  111775,99 m 2

 AC 
 421,33 m ABC
2
senb seng
seng
Triangolo A’BC l’angolo a’ si ricava facendo:
a’ = 180° - a = 105°,5965
b’ = 180° - a’ – g = 11°,6491
1
A' C
A' B
A' B  senb '
2

 A' C 
 125,11 m S A' BC   A' B  A' C  sena '  33190,83 m
senb ' seng
seng
2