Termodinamica
Prof. Graziano Surace
Ultima Rivisitazione: Roma, 15 Ottobre 2008
1
Prefazione
Questi appunti devono considerarsi solamente integrativi e non sostitutivi
alla lettura del libro di testo e allo studio domestico. Nella loro redazione ho
fatto attenzione al chiarimento di alcuni nodi concettuali che rappresentano
un ostacolo alla corretta comprensione dei concetti della termodinamica.
2
Il mondo della termodinamica
La termodinamica si occupa principalmente delle trasformazioni di calore in
lavoro meccanico e delle trasformazioni inverse di lavoro meccanico in calore.
2.1
Energia e Calore
Il calore è una forma di energia che può essere trasformata in altre forme di
energia. In passato gli scienziati pensavano che il calore fosse una sorta di
fluido indistruttibile (calorico) e interpretavano il processo di riscaldamento
di un corpo semplicemente come il flusso di questo fluido da un corpo ad un
altro.
Oggi sappiamo che il principio fondamentale per comprendere l’equivalenza
tra calore ed energia meccanica risiede nell’interpretazione cinetica (teoria cinetica della materia), che riduce tutti i fenomeni termici a moti disordinati
di atomi o molecole. Sotto questo speciale punto di vista il calore potrebbe
essere pensato come una parte speciale della meccanica (riduzionismo meccanicista).
1
Il punto di vista in termodinamica pura è, tuttavia, differente: qui i principi sono assunti come postulati fondati sull’esperienza e si traggono conclusioni da essi senza entrare nel meccanismo cinetico dei fenomeni. Questo
modo di procedere ha il vantaggio di essere largamente indipendente da
ipotesi semplificatrici che vengono spesso introdotte quando si fanno considerazioni di meccanica statistica (è questa la branca della fisica che si occupa
della teoria cinetica della materia). Ne segue che i risultati termodinamici
sono generalmente molto precisi.
D’altro canto, è piuttosto insoddisfacente ottenere dei risultati senza essere in grado di vedere come vanno effettivamente le cose, ma, ahimè, questa
è la vita!
2.2
La Temperatura ed il Termometro
La temperatura è quella grandezza fisica che si misura col termometro. Esistono varie tipologie di termometri. Il classico termometro a mercurio è uno
strumento che sfrutta come principio fisico la dilatazione di un liquido (Hg)
per effetto di una somministrazione di calore.
Ponendo un termometro a contatto con un sistema per un certo intervallo
di tempo si stabilisce un equilibrio termico, ovvero entrambi si porteranno
alla stessa temperatura. Questo vale anche per due corpi qualsiasi che inizialmente si trovano a temperature differenti (principio zero della termodinamica).
2.3
Sistemi Termodinamici
Lo stato di un sistema in meccanica è conosciuto quando,in un dato istante,
sono note la posizione e la velocità di ciascun punto materiale del sistema.
Questo significa che se il sistema è costituito da N particelle le variabili da
conoscere sono 6N (Bisogna, infatti, conoscere per ogni particella le tre variabili spaziali (x, y, z) e le tre componenti della velocità (vx , vy , vz )).
Se consideriamo che il numero di particelle in gioco (nel nostro caso dell’ordine
di N ∼ 1023 ) si capisce allora quanto difficile risulti conoscere lo stato meccanico di un sistema.
Inoltre, questo modo di procedere sarebbe del tutto inutile in quanto le
quantità trattate in termodinamica (grandezze termodinamiche) fanno riferimento a proprità medie del sistema. Di conseguenza, una conoscenza dettagliata del sistema sarebbe superflua. In termodinamica si introduce, per2
tanto,un concetto di stato che è diverso da quello indicato, e, per nostra gioia,
molto più semplice.
2.4
Variabili di Stato Termodinamiche
Sistema composto da un fluido omogeneo.
Per questo tipo di sistema si possono misurare le seguenti grandezze: pressione p, temperatura T , volume V (Le proprietà geometriche del nostro sistema non sono caratterizzate solo dal suo volume ma anche dalla sua forma.
Tuttavia, la maggior parte delle proprietà termodinamiche sono largamente
indipendenti dalla forma e quindi il volume è l’unico parametro geometrico
che viene assegnato).
Sistema composto da un solido omogeneo.
In questo caso, per definire lo stato del sistema possiamo introdurre, oltre
alla temperatura T e al volume V , la pressione che si esercita nelle diverse
direzioni. Nella maggior parte dei casi, si fa l’ipotesi, tuttavia, che la pressione sia isotropa (stesso valore in tutte le direzioni) per cui occorre considerare, come nel caso dei fluidi, un solo valore di p. Per una data quantità di
sostanza contenuta nel sistema, la pressione, il volume e la temperatura non
sono quantità indipendenti; esse sono legate da una relazione la cui forma
generale è la seguente :
f (T, V, p) = 0
(1)
Nel caso di un gas perfetto la relazione (1) è facilmente riconoscibile:
P V = nRT
equazione
di stato
(2) di un gas
perfetto
Si noti come sia facile ricondursi ad una equazione del tipo (1) semplicemente
ponendo:
P V − nRT = 0
In ogni caso è ben visibile come le tre grandezze non siano indipendenti. Lo
stato del sistema è, quindi, completamente determinato se conosciamo due
fra le tre grandezze p, T , V .
Può risultare molto utile rappresentare pressione e volume su un piano
cartesiano (V, p). Per esempio si può rappresentare V sulle ascisse e p sulle
ordinate. In questa maniera ogni punto del piano (V, p) rappresenta uno
stato del sistema. I punti che rappresentano stati di uguale temperatura
appartengono (giacciono) su una curva che è detta isoterma.
3
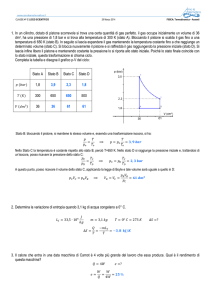
Piano di Clapeyron
p(atm)
Trasformazione Termodinamica
p1
A(V1,p1)
B(V2,p2)
p2
V1
V2
V(litri)
Figure 1: Trasformazione termodinamica da uno stato A(V1 , p1 ) ad uno stato
B(V2 , p2 )
2.5
Stati di equililibrio e trasformazioni termodinamiche
Tra gli stati termodinamici di un sistema particolare importanza assumono
gli stati d’equilibrio. Questi stati hanno la caratteristica di rimanere inalterati
se non cambiano le condizioni esterne. (Ad esempio, un gas contenuto in un
recipiente di volume costante è in equilibrio quando la pressione è costante
in ogni suo punto e la sua temperatura uguaglia quella del recipiente).
Molto spesso dovremo considerare trasformazioni di un sistema, da uno
stato iniziale ad uno stato finale, attraverso una successione continua di stati
intermedi. Su un diagramma (V, p) una trasformazione sarà rappresentata
da una curva che connette due punti del piano (Nel grafico di pagina lo stato
A(V1 , p1 ) e lo stato B(V2 , p2 )).
Si dice che una trasformazione é reversibile quando gli stati attraverso cui
il sistema passa durante la trasformazione differiscono pochissimo da stati di
equilibrio. Una trasformazione reversibile può, pertanto, connettere solo stati
di equilibrio (Ad esempio, si può ottenere una espansione reversibile di un
gas ponendolo in un cilindro con un pistone e spostando molto lentamente il
pistone verso l’esterno. Se spostassino il pistone molto velocemente si produrrebbero delle correnti all’interno della massa gassosa e gli stati intermedi
non sarebbero più stati di equilibrio).
4
P
Trasformazione Ciclica
Trasformazione ciclica di stato iniziale A
.
A
Pa
0
Va
V
Figure 2: Trasformazione ciclica di stato iniziale A(V1 , p1 ) coincidente con lo
stato finale
Se trasformiamo reversibilmente un sistema da uno stato A ad uno stato
B allora sará possibile riportare il sistema nuovamente allo stato A attraverso
una trasformazione inversa.
Sono particolarmente interessanti quelle trasformazioni in cui lo stato
iniziale e lo stato finale di un sistema coincidono. Simili trasformazioni sono
dette cicliche. Una trasformazione ciclica é rappresentata, nel piano (V, p),
da una curva chiusa (Vedi grafico seguente). Altre trasformazioni importanti,
per i nostri fini, sono:
• le trasformazioni isobare (p = cost);
• le trasformazioni isòcore (V = cost);
• le trasformazioni isoterme (T = cost);
Le trasformazioni isobare sono rappresentate, sul piano (V, p), da un segmento parallelo all’asse V (essendo p = cost) mentre le isòcore sono rappresentate da un segmento parallelo all’asse p (essendo V = cost).
5
2.6
Leggi dei gas ed Equazione di stato dei gas perfetti
L’equazione di stato di un sistema composto di una certa quantitá di gas
che occupa un volume V alla temperatuta T (temperatura assoluta espressa
in gradi Kelvin) e alla pressione p si può esprimere mediante una semplice
relazione:
P V = nRT
(3)
dove n rappresenta il numero di moli di gas (quantitá di gas) e R una costante
universale che vale per tutti i gas:
J
mol · K
dm3 · atm
= 0, 082057
mol · K
R = 8, 3144
(N.B : Nei calcoli tenere conto che 1dm3 = 1l e che 1atm = 101.325 · 103 P a)
L’equazione di stato dei gas perfetti contiene implicitamente le leggi di Boyle
e di Gay - Lussac.
Nessun gas gas reale obbedisce alla legge P V = nRT . Si chiama, pertanto,
gas perfetto una sostanza che obbedisce alla (3).
Legge di Boyle (1662)
A temperatura costante la pressione di un gas perfetto é inversamente proporzionale al volume occupato (o in altre parole il prodotto di p e V é
costante):
Legge di
P V = cost
(4) Boyle
Si noti come sul piano (V, p) la (4) corrisponda ad una iperbole equilatera.
Infatti p = Vk
Leggi di Gay - Lussac (1802)
Indicando con V0 (o p0 ) il volume (o la pressione) di un gas alla temperatura
di 0 gradi centigradi e con Vt (o pt ) il volume (o la pressione) del gas ad
una generica temperatura T > 0 (ancora in gradi centigradi) si ha:
• prima legge di Gay - Lussac:
V = V0 (1 + αT )
6
Prima
Legge di
(5) Gay Lussac
• seconda legge di Gay - Lussac:
p = p0 (1 + αT )
Seconda
Legge di
(6) Gay Lussac
dove α é un parametro detto coefficiente di espansione del gas e vale per
tutti i gas:
1
α=
(7)
273 ¦ C
2.7
Teoria cinetica dei gas. Interpretazione microscopica della temperatura
[Inserire contenuto (vedi Feynmann, Bergamaschini)]
3
3.1
Il primo principio della termodinamica
La conservazione dell’energia meccanica
Meccanica e Termodinamica sono due mondi separati? Tendenzialmente esse
lo sono solo nella didattica, per nostra fortuna la natura discrimina molto
meno!! Dovrebbe essere noto ai piú (e se non lo é meditate !!!) che la
conservazione dell’energia meccanica puó tradursi in una equazione del tipo:
Uiniziale + Kiniziale = Uf inale + Kf inale + Lattrito
(8)
dove con U si indica l’energia potenziale, con K l’energia cinetica e con Lattrito
il lavoro delle forze d’attrito (o piú in generale di forze passive).
D’altro canto é noto a tutti che quando un corpo striscia su una superficie la sua temperatura aumenta. Cosa ha prodotto questo aumento di
temperatura? La risposta é (tutti in coro! ): l’attrito. Potremmo dire che il
lavoro delle forze d’attrito si trasforma, si converte, integralmente in calore
che, ricordiamo, é una forma di energia (riconducibile al moto di particelle).
L’equazione appena scritta potrebbe allora essere abbellita nella maniera
seguente:
Uiniziale + Kiniziale = Uf inale + Kf inale + Q
(9)
dve Q é il calore ceduto dal sistema sotto forma termica nella sua evoluzione
temporale.
7
FP
L
ªH
S
Figure 3: Gas racchiuso in un cilindro munito di pistone scorrevole soggetto
ad una pressione esterna p = FS
Il legame tra mondo meccanico e mondo termodinamico diventa cosı́ piú
chiaro. Il legame si chiama ”principio di conservazione dell’energia” e risale,
nella sua formulazione attuale, alla metá del XIX secolo. Non esiste una
data precisa (mi dispiace!) perché piú persone, in periodi differenti, hanno
contribuito alla scoperta, se di scoperta si puó parlare (Si tratta, infatti, di
un principio).
NOTA di carttere culturale a titolo puramente personale: talvolta é riduttivo parlare di semplici persone se i soggetti in questione sono: Christiaan Huygens (fisico tedesco), Gottfried Wilhelm von Leibniz (filosofo,
fisico, matematico e avvocato tedesco) Julius Robert von Mayer (medico
e fisico tedesco), William Thomson (al secolo, Lord Kelvin, fisico britannico), James Prescott Joule (birraio e fisico inglese), Nicolas Léonard
Sadi Carnot (ingegnere e fisico francese), Rudolf Julius Emanuel Clausius
(fisico e matematico tedesco).
3.2
Lavoro Termodinamico
Ma non bastava il lavoro meccanico (prodotto tra il modulo di una forza
e il modulo dello spostamento (nella direzione della forza))? La risposta é
evidentemente N O. Il lavoro temodinamico, tuttavia, non é che una estensione del concetto di lavoro meccanico.Cerchiamo di capire questo concetto
servendoci di un esempio tipico di termodinamica.
Consideriamo un sistema costituito da un gas racchiuso in cilindro munito
di pistone scorrevole, senza attrito (Vedi figura 3). Supponiamo che io muova
8
molto lentamente il pistone dall’esterno (compressione del gas all’interno del
pistone). In pratica sto esercitando un forza esterna (costante) sull’ambiente
in cui é racchiuso il gas, in particolare sulla superficie S del pistone. Sto
esercitando, quindi, una pressione esterna pest sul pistone.
Remarks: Anche il peso dell’aria esercita un certa pressione esterna sulla
superficie del pistone (pressione atomsferica patm ) che andrebbe considerata.
A rigore quindi la pressione esterna totale, p, vale: p = pest + patm .
In virtú di questa pressione esterna il pistone inizierá a scendere di livello (in
figura il dislivello é stato indicato con 4h). L’obiettivo che ci proponiamo
é quello di calcolare il lavoro che la forza esterna compie sul pistone. Ricordandoci che il lavoro meccanico é dato dal prodotto tra forza e spostamento
nella direzione della forza (con ovvietá di simboli: L = Fs S), si ha, dunque,
che il lavoro delle forze esterne é uguale a:
L = F 4h
(10)
Dalla definizione di pressione p = FS si ha immediatamente che F = pS.
Sostituendo nella (10) si ha dunque:
L = pS4h
(11)
Ma S4h non é altro che il volume di gas compresso 4V (In altre parole:
4V = S4h ). Questo permette di scrivere:
lavoro
L = p4V
La (12) é la formula con cui si calcola il lavoro termodinamico prodotto
da una certa pressione esterna costante. Lo stesso discorso potrebbe essere
ripetuto pedissequamente se invece della pressione esterna considerassimo
la pressione interna del gas; l’unica differenza consisterebbe nel considerare
una espansione del gas (aumento di volume del gas contenuto all’interno del
cilindro) anziché una compressione.
Remarks:
• Le trasformazioni considerate negli esempi sono delle trasformazioni
quasi statiche (reversibili) in cui si é sostanzialmente assunto che la
pressione (esterna o interna del gas) non cambi. Ci siamo riferiti,
dunque, a trasformazioni isobare;
• Per convenzione, si assume positivo (L > 0) il lavoro di espansione
di un gas ai danni dell’ambiente esterno; si assume negativo (L < 0)
9
termo-
(12) dinamico
il lavoro di compressione compiuto dall’ambiente esterno a spese del
gas (in pratica il lavoro compiuto dal gas é opposto al lavoro compiuto
dall’esterno sul gas);
• Anche il lavoro termodinamico, come pure quello meccanico, si misura
in Joule, essendo il lavoro una forma di energia con cui il sistema (gas
+ cilindro) scambia energia con l’ambiente esterno.
3.3
Equivalenza tra calore e lavoro. Esperienza di Joule
[Inserire contenuto (Vedi Fermi, Bergamschini, Caforio)]
3.4
Formulazione analitica del primo principio della
termodinamica
Il primo principio della termodnamica é essenzialmente il principio di conservazione dell’energia per sistemi termodinamici.
Ricordiamo che, in base alla teoria cinetica dei gas, il calore fornito ad un
sistema viene impegnato per aumentarne il contenuto energetico complessivo
(energia interna, U ). Avevamo gi osservato come somministrando calore ad
un sistema l’energia cinetica media delle molecole aumentasse e come questo
aumento di energia fosse legato all’aumento di temperatura. In sostanza,
dunque, la somministrazione di calore aumenta l’energia termica (o interna)
di un sistema, in assenza di lavoro meccanico! Volendo essere ancora piú
energia
espliciti si puó dire che:
U = U (T )
(13) interna
(leggi: ”U dipende da T ”).
Prima di passare alla formulazione analitica del principio consideriamo i
due esempi della figura:
Caso (A). Supponiamo che una certa quantitá diaeriforme sia contenuta
all’interno di un recipiente di volume V a pareti rigide. Se forniamo all’aeriforme
una certa quantitá di calore Q allora aumenterá anche la temperatura T
dell’aeriforme (essendo V fissato). Ma se aumenta la temperatura allora aumenterá anche l’energia interna dell gas che passerá da un certo valore U1 ad
un altro valore U2 . Dunque il calore Q provoca una variazione dell’energia
interna 4U . In formule:
Q = 4U
10
pa
Pistone mobile
V, pi
V, p
Gas
Gas
Sorgente di calore
Sorgente di calore
(B)
(A)
Aeriforme contenuto in un
Recipiente di volume V a
Pareti rigide
Aeriforme contenuto in un
Cilindro dotato di pistone
A tenuta
Figure 4: (A): Aeriforme contenuto in un recipiente di volume V a pareti
rigide; (B): Aeriforme racchiuso in un cilindro munito di pistone scorrevole
Caso (B). Supponiamo ora che l’aeriforme sia contenuto in un cilindro
dotato di pistone scorrevole di peso trascurabile. Inizialmente (prima di
iniziare a fornire calore) la pressione interna del gas, pi , uguaglia la pressione
atmosferica pa . Quando iniziamo a fornire calore, Q, la temperatura del gas
aumenta (e quindi c’éuna variazione di energia interna 4U ) ed inoltre il gas
si espande compiendo lavoro L (come visto nel paragrafo 3.2). In formule
quindi :
Q = 4U + L
Questa formula rappresenta la formulazione analitica del cosiddetto primo
principio della termodinamica.
11
primo
principio
della
termodinamica