Fisica 2 (5 CFU)
Cognome
CCS
Appello A.A. 2010-2011
n. matricola
Nome
Docente
22.02.2012
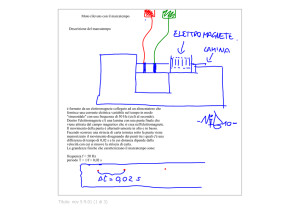
Esercizio 1. In una regione di spazio a forma di cilindro di raggio a è distribuita una carica con densità
(r)=0(1+br). Ad una distanza r1 dall’asse del cilindro il campo elettrico vale E(r1) ed il potenziale
elettrostatico vale V(r1).
Calcolare:
1) il valore della costante 0
2) il valore della costante b
3) il valore del campo sul bordo della regione cilindrica (r=a)
4) il valore del potenziale sul bordo della regione cilindrica (r=a)
Utilizzare per i calcoli: a=20 cm, r1=5cm, E(r1)=120 V/m, V(r1)=10V
Dal teorema di Gauss 𝐸(𝑟) =
𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑛𝑑𝑜 𝑠𝑖 𝑜𝑡𝑡𝑖𝑒𝑛𝑒
∆𝑉(𝑟) =
𝜌0
𝜀0
1
1
𝑟 (2 + 3 𝑏𝑟)
𝜌0 𝑟 1 1
𝜌0
1 1
∫ ( + 𝑏𝑟) 𝑟𝑑𝑟 = 𝑟 2 ( + 𝑏𝑟)
𝜀0 0 2 3
𝜀0
4 9
Dalle due eq. Precedenti:
9[𝐸(𝑟)𝑟−2∆𝑉(𝑟)]
𝑏 = 4𝑟[3∆𝑉(𝑟)−𝐸(𝑟)𝑟]= -10 m-1
𝜌0 =
𝜀0 𝐸(𝑟)
1 1
2 3
( + 𝑏𝑟)𝑟
= 6.4 10-8C/m3
E(r = a) = -240 V/m
V(r = a) = V(r=a) + cost.
dove V(r=a) = 8V
n.b.: il pot. e.s. V è definito a meno di una costante
Esercizio n.2 In una striscia metallica infinitamente lunga e di larghezza h, costituita da un numero praticamente
infinito di fili conduttori, ognuno dei quali può essere considerato di spessore infinitesimo, scorre una corrente i.
In un punto, che giace sul piano della striscia ad una distanza y2>>h dalla striscia, il campo di induzione
magnetica vale B2. Calcolare:
1)
la corrente che scorre nella striscia
2)
il campo di induzione magnetica B1 in un punto y1 che giace sul piano della striscia ad una
distanza 3h dal bordo della striscia.
Utilizzare per i calcoli numerici: h=10 cm, y2=10 m, B2=4T
i=
𝐵2 2𝜋𝑦2
𝜇0
=200 A
Nel punto y1 avremo:
𝜇 𝑑𝑖
𝑑𝐵 = 2𝜋(𝑦0
1 −𝑦)
dove
di=(i/h)dy
𝜇 𝑖
ℎ
2
ℎ
𝑦1 −
2
𝑦1 +
0
quindi integrando 𝐵1 = 2𝜋ℎ
𝑙𝑛 (
)=0.2 mT